Espiral giratória: matemática e alucinações

Ao tentar imaginar alucinações causadas por substâncias entorpecentes, surgem formas psicodélicas em espiral, em espiral, que se assemelham imediatamente à visão do túnel . Mas essas estruturas geométricas podem causar não apenas drogas alucinógenas como LSD, cannabis ou mescalina . As pessoas falavam sobre o aparecimento de tais visões no momento em que estavam mortas, em condições dolorosas como epilepsia e esquizofrenia, como resultado de privações sensoriais ou mesmo após uma simples pressão nos olhos. Tais alucinações geométricas são tão difundidas que, no século passado, os cientistas começaram a se perguntar se poderiam nos dizer algo fundamental sobre a estrutura do nosso cérebro. E, aparentemente, é.


Constantes de formulário criadas em um computador. As duas imagens superiores imitam o funil e a espiral que ocorrem após o recebimento de LSD. O canto inferior esquerdo é o favo de mel criado pela maconha. O canto inferior direito é a web.

Alucinações geométricas sistemáticas começaram a ser investigadas na década de 1920 por um psicólogo americano-alemão, Heinrich Kluver . O interesse de Kluver pela percepção visual levou-o a experimentar o peiote , um cacto, comemorado por Carlos Castaneda , cujo ingrediente psicoativo, mescalina, desempenhou um papel importante nos rituais xamanísticos de muitas tribos da América Central. A mescalina é bem conhecida por causar alucinações visuais vívidas. Usando peiote no laboratório com um assistente, Kluver notou repetir formas geométricas em alucinações causadas pela mescalina e as dividiu em quatro tipos, chamando-as de constantes : túneis e funis, espirais, treliças, que incluem favos de mel e triângulos e teias de aranha.

Na década de 1970, os matemáticos Jack Cowan e Bard Ermentraut usaram a classificação de Kluver para criar uma teoria que descreve o que acontece no cérebro quando nos faz acreditar que vemos padrões geométricos. Sua teoria foi desenvolvida por outros cientistas, incluindo Paul Breslov, professor de neurobiologia matemática e computacional do recém-fundado Oxford Center for Collaborative Applied Mathematics.

Onde estão as tiras do córtex cerebral *

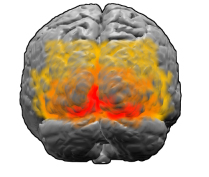O córtex visual. Área marcada em vermelho V1

[ * Referência ao conto de fadas vietnamita “De onde vem o tigre” / aprox. perev. ]

A primeira área do córtex visual do cérebro que processa imagens em humanos e mamíferos é a área conhecida como V1. Evidências experimentais, como imagens de fMRI , sugerem que os padrões de Kluver também vêm principalmente da V1 e não aparecem mais tarde em algum lugar do sistema visual. Como o resto do cérebro, V1 tem uma estrutura complexa, enrugada e dobrada - no entanto, há uma maneira surpreendentemente direta de traduzir o que vemos em nosso campo de visão na atividade dos neurônios em V1. "Imagine que estamos implantando a V1", diz Breslov. - Pode ser imaginado como um tecido nervoso com vários milímetros de espessura, com várias camadas de neurônios. Em uma primeira aproximação, os neurônios em toda a profundidade do córtex se comportam de maneira semelhante; portanto, se você os achatar, poderá imaginar V1 como uma folha bidimensional ".

O objeto ou cena do mundo visual é projetado na forma de uma imagem bidimensional na retina de cada olho, de modo que o que vemos também pode ser considerado como uma folha plana: campo de visão. Cada ponto nesta planilha pode ser designado por duas coordenadas, como um ponto no mapa ou um ponto em um modelo plano V1. As áreas claras e escuras alternadas que compõem as alucinações geométricas são causadas pelas áreas alternadas de alta e baixa atividade dos neurônios em V1 - áreas onde os neurônios são ativados muito rapidamente e áreas onde o oposto é verdadeiro.

Para converter padrões visuais em atividade neuronal, é necessária uma grade de coordenadas - uma regra segundo a qual cada ponto do campo de visão é conectado a um ponto do modelo de plano V1. Na década de 1970, cientistas, incluindo Cowen, fizeram uma grade com base no conhecimento da anatomia da interação dos neurônios da retina com os neurônios da V1. Para cada parte clara ou escura do campo de visão, o mapeamento define uma parte da atividade neuronal alta ou baixa em V1.

Como essa imagem da retina e do córtex transforma os padrões geométricos de Kluver? Acontece que as alucinações, causando espirais, círculos e raios que emanam do centro, correspondem às faixas de atividade dos neurônios em V1 que passam em ângulos determinados. Malhas como favos de mel ou células correspondem aos padrões hexagonais de atividade em V1. Isso por si só pode não ser tão interessante, mas há um precedente: foram as listras e hexágonos que os cientistas observaram ao modelar outros exemplos de formação de padrões, por exemplo, convecção de líquidos ou, mais surpreendentemente, o aparecimento de manchas e listras nas peles de animais. A matemática que governava a formação desses padrões era bem conhecida e também propunha um mecanismo para modelar o funcionamento do córtex visual.

Do campo de visão ao córtex visual

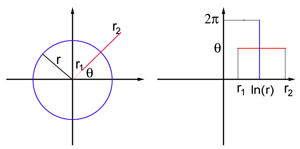
Imagine o campo de visão na forma de uma folha plana com coordenadas polares: cada ponto P é definido por dois números (r, θ), onde r é a distância da origem e θ é o ângulo entre o segmento OP e o eixo x. O ponto de referência corresponde ao centro do campo de visão. V1 também é modelado como uma folha plana, mas desta vez tendo coordenadas cartesianas (x, y). A exibição exata das coordenadas do campo de visão e do modelo de plano V1 é muito complicada para este artigo, mas para pontos suficientemente distantes do centro do campo de visão (ou seja, para um r suficientemente grande), ela se assemelha a um mapa logarítmico:

$$

$$x = \ ln {r} \\ y = \ theta$$

O mapeamento traduz um círculo de raio r no campo de visão em um segmento vertical reto com x = ln r, e um raio proveniente da origem das coordenadas O em um ângulo θ em um segmento horizontal reto com y = θ

Onde o local do leopardo

O primeiro modelo para a formação de padrões de pele de animais remonta a Alan Turing , mais conhecido como o pai da ciência da computação moderna e um hacker de Bletchley Park que decifrou códigos. Turing estava interessado em como um sistema espacialmente homogêneo, como uma bola uniforme de células, que é o embrião de um animal, pode criar padrões espacialmente não homogêneos, mas estáticos, como listras de zebra.

Turing sugeriu que esses padrões aparecessem como resultado de um processo de difusão de reação . Imagine um embrião animal em cuja pele vivem dois compostos químicos. Um deles é um inibidor que suprime a produção de si mesmo e de outro produto químico. O outro é um catalisador que causa a produção de ambas as substâncias.

No momento inicial do modelo de Turing, dois produtos químicos se equilibram idealmente - eles estão em equilíbrio, e sua concentração em diferentes pontos do embrião não muda com o tempo. Agora imagine que, por algum motivo, em um ponto, a concentração de catalisador tenha aumentado ligeiramente. Essa pequena perturbação coloca todo o sistema em movimento. O aumento da concentração local do catalisador significa que mais catalisador e inibidor são produzidos lá. No entanto, ambos os compostos também se difundem sobre a pele do embrião, inibindo e catalisando sua produção em outros locais.

Por exemplo, se um inibidor se difunde mais rapidamente que um catalisador, ele rapidamente envolve o ponto de perturbação e reduz a concentração de catalisador nele. Como resultado, obtemos uma seção com uma alta concentração de catalisador, cercada por uma alta concentração de inibidor - em outras palavras, uma mancha de catalisador no fundo do inibidor. Dependendo da taxa de difusão dos dois compostos, é possível que esse padrão manchado apareça por toda a pele do embrião e eventualmente se estabilize.

Thuring escreveu um sistema de equações diferenciais descrevendo a competição entre os dois compostos - você pode deixá-los desenvolver-se a tempo e ver se os padrões aparecem. Essas equações dependem dos parâmetros que descrevem a taxa de difusão de dois compostos: se você os selecionar corretamente, o sistema eventualmente se estabiliza, formando um determinado padrão que pode ser alterado alterando os parâmetros. O link fornece um applet em Java , no qual você pode brincar com os parâmetros e observar os padrões resultantes.

Equações de padrões animais

Para simplificar, imagine um embrião na forma de uma linha unidimensional. A qualquer momento t e em qualquer ponto x do embrião, a concentração do catalisador (ativador) e inibidor (inibidor) é determinada pelas funções A (x, t) e I (x, t). Eles mudam ao longo do tempo de acordo com as seguintes regras:

$$

$$\ frac {\ parcial A} {\ parcial t} = f (A, I) + \ frac {\ parcial ^ 2 A} {\ parcial x ^ 2} \\ \ frac {\ parcial I} {\ parcial t } = g (A, I) + d \ frac {\ parcial ^ 2 I} {\ parcial x ^ 2}$$

O primeiro termo à direita de cada equação descreve a quantidade de produção de catalisador e inibidor. São funções das concentrações de catalisador e inibidor, pois ambos afetam a taxa de reação.

O segundo termo à direita de cada equação é a segunda derivada, que descreve a taxa de variação do gradiente do catalisador e inibidor. Eles definem a taxa de difusão.

Um termo adicional d no lado direito da segunda equação é o coeficiente de difusão, que mostra o quanto o inibidor se difunde mais rapidamente que o catalisador. Turing mostrou que a superioridade na velocidade do inibidor é um parâmetro crítico para a geração de manchas.

Padrões cerebrais

A atividade dos neurônios no cérebro não é um processo difuso de reação, no entanto, tem analogias com o modelo de Turing. "Os neurônios enviam sinais entre si através dos canais de saída de dados chamados axônios", diz Breslov. Os neurônios reagem aos sinais um do outro, aqui está a reação. "Os sinais viajam tão rápido em comparação com o processo de padronização que podem ser confundidos com interações instantâneas". Portanto, em vez de difusão, um processo local, temos interação instantânea à distância. Os papéis de catalisador e inibidor são desempenhados por duas classes diferentes de neurônios. "Existem neurônios excitatórios - que aumentam a probabilidade de outros neurônios se tornarem ativos - e há neurônios inibitórios que reduzem essa probabilidade", diz Breslov. "A competição entre as duas classes de neurônios é análoga ao mecanismo inibidor de catalisador no modelo de Turing".


Padrões listrados, hexagonais e retangulares de atividade nervosa em V1 gerados por um modelo matemático

Inspirados pelas analogias dos processos de Turing, Cowan e Ermentraut criaram um modelo de atividade nervosa em V1 usando um conjunto de equações formuladas por Cowan e Hugh Wilson. Embora as equações tenham sido mais complicadas que as de Turing, você ainda pode jogar o mesmo jogo, permitindo que o sistema evolua ao longo do tempo e veja se os padrões de atividade nervosa se desenvolvem. "Você pode descobrir que, sob certas condições, se você aumentar o parâmetro, representando, por exemplo, o efeito de drogas no córtex, isso levará ao crescimento de padrões periódicos", diz Breslov.

O modelo de Cowan e Ermentraut sugere que as alucinações geométricas resultam da instabilidade na V1: alguma coisa, por exemplo, a presença de uma droga, remove a rede neural de um estado equilibrado, iniciando um processo crescente de interação entre neurônios estimulantes e suprimidores, que estabiliza na forma de padrões listrados ou hexagonais de atividade nervosa em V1. Então, “observamos” esse padrão na forma de estruturas geométricas descritas por Kluver no campo de visão.

Simetrias no cérebro

De fato, nem tudo é tão simples quanto no modelo de Cowan e Ermentraut, uma vez que os neurônios respondem não apenas a imagens claras e escuras. Pela espessura V1, os neurônios se alinham em colunas conhecidas como hipercolunas , cada uma das quais responde aproximadamente a uma pequena parte do campo visual. Mas nem todos os neurônios da hipercoluna são iguais: além de reconhecer as áreas claras e escuras, cada neurônio é especializado em reconhecer rostos locais - linhas que separam áreas claras e escuras em uma parte da imagem - uma certa orientação. Alguns reconhecem faces horizontais, outras - verticais, outras - faces localizadas em um ângulo de 45 ° e assim por diante. Cada hipercoluna contém colunas de neurônios de todas as orientações preferidas; portanto, uma hipercoluna pode responder às faces de todas as orientações em uma determinada área do campo visual. É a composição das hipercolunas e preferências de orientação que nos permitem reconhecer os contornos, superfícies e texturas do mundo visual.


Conexões em V1: neurônios em uma hipercoluna interagem com a maioria dos outros neurônios. Mas eles reagem com neurônios em outras hipercolunas apenas se as colunas estiverem localizadas na direção de sua orientação, e os neurônios tiverem a mesma preferência de orientação.

Nos últimos anos, muitas evidências anatômicas foram coletadas sobre como os neurônios interagem entre si com diferentes preferências de orientação. Dentro da coluna geográfica, os neurônios interagem com a maioria dos outros neurônios, independentemente de suas preferências. Mas, quanto aos neurônios de outras hipercolunas, eles agem de maneira mais seletiva, interagindo apenas com neurônios de preferências semelhantes, de modo a garantir a capacidade de reconhecer contornos contínuos no mundo visual.

Breslov, juntamente com Cowen, o matemático Martin Golubitsky e outros cientistas, generalizou o modelo original de Cowen e Ermentraut para levar em conta essas novas evidências anatômicas. Eles novamente usaram o plano como base do modelo V1: cada hipercoluna é representada no plano por um ponto (x, y), e cada ponto (x, y) corresponde a uma hipercoluna. Os neurônios com uma dada preferência pela orientação θ (onde θ é o ângulo entre 0 e π são indicados pela posição da hipercoluna (x, y) juntamente com o ângulo θ - ou seja, são indicados por três unidades de informação (x, y, θ). Os modelos V1 não são um plano, mas um plano com um conjunto completo de orientações para cada ponto.


Se dois elementos, (x, y, θ) e (s, t, θ) interagem, outros elementos com a mesma orientação interagem nos pontos (x + a, y + b) e (s + a, t + b ) e elementos com a orientação -θ nos pontos (x, -y) e (s, -t).

Para cumprir as evidências anatômicas, Breslov e colegas sugeriram que o neurônio indicado pelo ponto (x ₀ , y ₀ , θ ₀ ) interaja com todos os outros neurônios na mesma hipercoluna (x ₀ , y ₀ ). Mas ele interage com neurônios de outras hipercolunas apenas se eles estiverem na orientação preferida θ ₀ : no plano, é necessário desenhar uma linha através do ponto (x ₀ , y ₀ ) em um ângulo θ ₀ . Em seguida, os neurônios indicados pelo ponto (x ₀ , y ₀ , θ ₀ ) interagem apenas com os neurônios das hipercolunas na mesma linha, ou seja, tendo a mesma orientação preferida θ ₀ .

Esse esquema de interação é muito simétrico. Por exemplo, ele não muda quando o avião é deslocado em qualquer direção por qualquer distância: se dois elementos (x ₀ , y ₀ , θ ₀ ) e (s ₀ , t ₀ , φ ₀ ) interagem, os elementos obtidos pela mudança, (x ₀ + a, y ₀ + b, θ ₀ ) e (s ₀ + a, t ₀ + b, φ ₀ ) para alguns a e b, interagem da mesma maneira. Pelo mesmo princípio, o esquema é invariável em relação às rotações e reflexões do plano.


Uma alucinação de treliça criada por um modelo matemático. Assemelha-se fortemente às alucinações que ocorrem ao consumir maconha.

Breslov e colegas usaram uma versão generalizada das equações do modelo original para permitir o desenvolvimento do sistema. O resultado é um modelo que não é apenas mais preciso em termos de anatomia da V1, mas também capaz de gerar padrões geométricos no campo de visão de que o modelo original não era capaz. Isso inclui túneis de treliça, favos de mel e teias de aranha, cuja orientação os caracteriza melhor do que áreas contrastantes claras e escuras.

Além disso, o modelo é sensível às simetrias dos esquemas de interação dos neurônios: os matemáticos mostraram que são essas simetrias que geram a formação de padrões periódicos de atividade nervosa. Portanto, o modelo pressupõe que alucinações dão origem ao arranjo de hipercolunas e preferências de orientação, ou seja, mecanismos que nos ajudam a reconhecer as faces, contornos, superfícies e texturas do mundo visual. É quando esses mecanismos perdem a estabilidade, por exemplo, como resultado da exposição à droga, aparecem padrões de atividade que se transformam em alucinações visuais.

Além das alucinações

O modelo de Breslov não apenas permite obter uma visão dos mecanismos que geram alucinações visuais, mas também fornece pistas sobre a arquitetura do cérebro em um sentido mais amplo. Juntamente com sua esposa, um neurobiologista experimental, Breslov estudou os contornos das conexões da hipercoluna com a visão normal para entender como as imagens visuais são processadas. “As pessoas estão acostumadas a acreditar que os neurônios da V1 simplesmente definem as faces locais e que é preciso ir para níveis mais altos do cérebro para coletar essas faces e reconhecer coisas mais complexas, como contornos e superfícies. Mas, com nosso trabalho com minha esposa, fica claro que essas estruturas em V1 permitem que o córtex visual reconheça contornos em um estágio inicial e conduza um processamento mais global. Acreditava-se que processamos aspectos cada vez mais complexos da imagem, subindo mais na hierarquia do cérebro. Agora ficou claro que há um feedback ativo entre as partes superior e inferior do córtex."Este não é um processo hierárquico simples, mas um sistema incrivelmente complexo e ativo, que levará muitos anos para ser entendido."

Entre as aplicações práticas deste trabalho está a visão computacional - os cientistas da computação já estão construindo estruturas com conexões internas com as quais Breslov e colegas brincaram para criar modelos para ensinar aos computadores como definir contornos e texturas. Se você mostrar um pouco de imaginação, pode imaginar que algum dia esse estudo poderá ajudar a restaurar a visão das pessoas com deficiência. "A questão é se é possível, de alguma forma, estimular parte do córtex visual, contornando o olho e usá-lo para orientar os cegos", diz Breslov. "Se você entender como o córtex está estruturado e como ele reage à estimulação, talvez seja possível inventar o melhor método para sua estimulação correta".

Existem até áreas de aplicação que não estão de todo conectadas com o cérebro. Breslov aplicou as idéias obtidas em seu trabalho a outras situações em que os objetos estão localizados em um espaço com uma certa orientação, por exemplo, fibroblastos de tecidos humanos e animais. Ele mostrou que, sob certas condições, essas células e moléculas em interação podem se alinhar e produzir padrões semelhantes aos que aparecem na V1.

As pessoas falavam em ver alucinações desde o início dos tempos, e em quase todas as culturas - imagens de alucinações podem ser encontradas em petroglifose pinturas rupestres. Nas tradições dos xamãs de todo o mundo, eles são tratados como mensagens do mundo dos espíritos. Poucos neurocientistas modernos concordam com o envolvimento dos espíritos nisso, mas como mensageiros do mundo oculto - desta vez, o mundo oculto do nosso cérebro - essas alucinações não perderam suas capacidades.