Outro dia, o YouTube achou que seria interessante assistir a um vídeo intitulado "A IA aprende a jogar Hill Climb Racing". É engraçado, porque alguns minutos antes eu havia comprometido as próximas mudanças no projeto, onde meus colegas e eu, entre trabalho e trabalho, resolvemos esse problema. É verdade que não havia "IA" naquele
vídeo - o autor entreteve o público com indulgência com o Box2D e se acalmou. No entanto, proponho considerar esse fato uma prova convincente da relevância do tópico e desmontar o dispositivo de nosso chocalho.
Brevemente sobre a tarefa: o veículo - no nosso caso, é o Alien, ou a máquina de costura Singer sobre rodas, vamos chamá-lo simplesmente de “agente” - deve percorrer as dunas com o mesmo
ruído do início ao fim. É assim que o agente se parece em sua sandbox:
Um agente que toca a parte de trás da pista ou não mostra zelo adequado ao se mover em direção à meta é removido da pista.
Vamos resolver o problema usando redes neurais, mas otimizadas pelo algoritmo genético (GA) - esse processo é chamado de
neuroevolução . Utilizamos o método NEAT (NeuroEvolução de Topologias Aumentadas), inventado por Kenneth Stanley e Risto Miikkulainen no início do século
[1] : primeiro, ele trabalhou bem em
problemas importantes para a economia nacional e, em segundo lugar, começamos a trabalhar no projeto já possuía sua própria estrutura implementando o NEAT. Portanto, francamente, não escolhemos um método de solução - escolhemos uma tarefa em que você pode conduzir o que já está pronto.
A figura mostra um esquema aproximado de algoritmos genéticos:
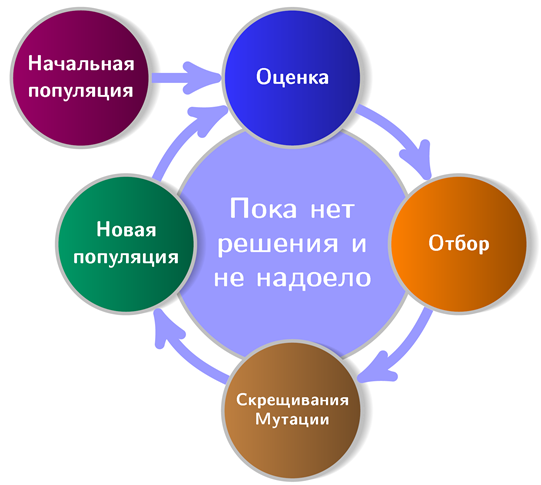
Pode-se observar que qualquer AG decente começa na população inicial (a
população é um conjunto de possíveis soluções). Estaremos envolvidos em sua criação e, ao mesmo tempo, familiarizar-nos com o
primeiro princípio da NEAT . De acordo com esse princípio, todos os agentes da população inicial devem ter a topologia mais simples e "mínima" da rede neural. O que a topologia tem a ver com isso? O fato é que, na NEAT, juntamente com a otimização dos pesos de conexão, a arquitetura de rede também evolui. A propósito, isso elimina a necessidade de seu design para a tarefa. Ir de arquiteturas simples para arquiteturas complexas não é apenas lógico, mas também prático (há menos espaço de pesquisa); portanto, você precisa começar com o mínimo de topologias possíveis - é assim que os autores do método pensaram.
Para nossos e todos os casos semelhantes, essa topologia mínima é derivada das seguintes considerações. Para fazer algo significativo, o agente precisa:
- ter informações sobre o meio ambiente e suas condições,
- processar esta informação
- interaja com o seu mundo.
O primeiro papel é desempenhado pelos
sensores - neurônios da camada de entrada, aos quais forneceremos informações úteis para o agente. Os neurônios da camada de
saída processarão os dados dos sensores.
Os atores - dispositivos que executam ações mecânicas em resposta a um sinal do "seu" neurônio da camada de saída - são responsáveis por interagir com o ambiente. Assim, o princípio geral de construir a configuração inicial é o seguinte: determinamos com sensores e atuadores, iniciamos um neurônio por atuador, conectamos todos os sensores e mais um neurônio especial - um
neurônio de deslocamento (
viés , sobre isso abaixo) com pesos aleatórios para todos os neurônios camada de saída. Algo assim:
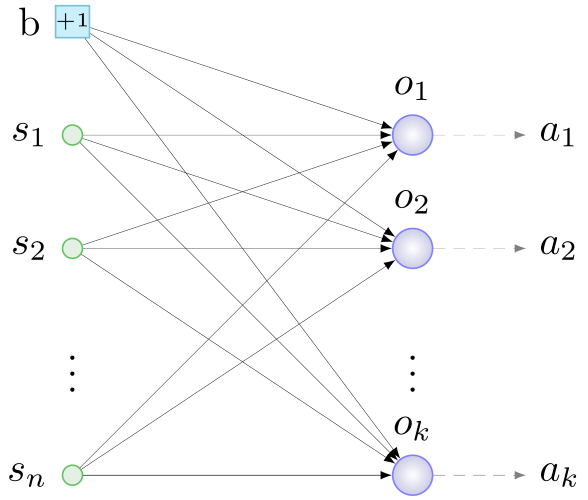b - polarização, s - sensores, o - neurônios da camada de saída, a - atuadores, n - número de sensores, k - número de atuadoresE aqui está o NS mínimo para nossa tarefa:
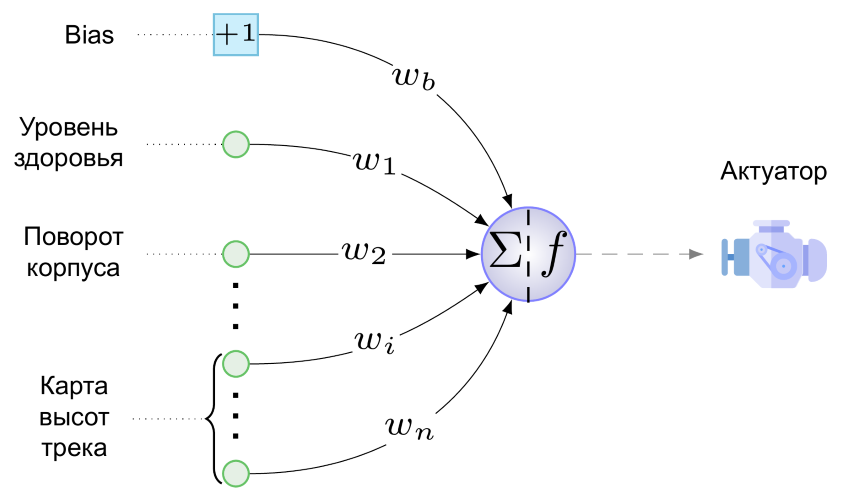
Temos apenas um atuador - este é o motor de nossa criação com rodas. Ainda não sabe atirar, pular e tocar cachimbo. O seguinte valor é fornecido ao mecanismo a partir de um único neurônio da camada de saída (é uma pena chamá-lo de camada):
Aqui w
b é o valor do peso da conexão que passa do viés para o neurônio de saída, multiplicado pelo fato de que qualquer viés "produz", isto é, +1, s
i é o valor normalizado para a faixa [0,1] no i-ésimo sensor, w
i é o valor do peso da conexão do i-ésimo sensor ao neurônio de saída ef é a função de ativação.
Como uma função de ativação, usamos esta fantasia de design suave:
- Ela demonstrou o melhor desempenho em testes de um neuro-evolucionista conhecido em círculos estreitos
[2] . E não faz sentido comparar a suavidade das dobras e a simetria do gráfico dessa função com a Leaky ReLU com inclinação angular:
Esta figura mostra a reação do agente a diferentes valores da função de ativação. Em valores próximos à unidade, o motor gira as rodas no sentido horário, acelerando o agente para a frente e inclinando fortemente a carcaça para trás, de modo que os fracos, mas corajosos, rapidamente tombem sobre as costas e morram. Com valores próximos a 0, o oposto é verdadeiro e, com um valor de 0,5, o motor do agente não funciona.
A mesma figura mostra o papel do neurônio de viés - o peso da ligação que vai dele para o neurônio da camada de saída é responsável, conforme segue (1), pela magnitude e direção do viés f (x) ao longo da abcissa. A linha pontilhada na figura mostra um gráfico da função de ativação em w
b = -1. Acontece que, mesmo na ausência de um sinal nos sensores, um agente com essa conexão retornará rapidamente: f (x) = f (-1 + 0) ± 0,083 <0,5. Em geral, a alteração horizontal dos valores da função permite que a conexão polarizada ajuste sutilmente (bem ou grosso, dependendo do peso) a reação do motor a todos os valores do sensor e o peso de suas conexões ao mesmo tempo. Parece que uma nova dimensão foi adicionada ao espaço de pesquisa (o valor "correto" de w
b precisará ser pesquisado), mas os benefícios na forma de um grau adicional de liberdade superam a possibilidade de tais deslocamentos.
Bem, apresentamos as redes neurais de agentes da futura população inicial. Mas o NEAT é um algoritmo genético e funciona com
genótipos - as estruturas das quais as redes são formadas ou, de maneira mais geral,
fenótipos no processo de decodificação. Desde que começamos com o fenótipo, faremos tudo ao contrário: tente codificar a rede apresentada acima no genótipo. Aqui você não pode prescindir do
segundo princípio NEAT , cuja essência principal é a seguinte: no genótipo, além da estrutura da rede neural e dos pesos de suas conexões, as informações são armazenadas na história da origem de todos os seus elementos. Com exceção desse aspecto histórico, o fenótipo é codificado no genótipo quase “um para um”, portanto, agora ilustraremos o segundo princípio com fragmentos de redes neurais.
É difícil superestimar o valor desse princípio - ele fornece aos agentes a possibilidade de reprodução sexual. O assunto é bastante delicado, portanto, consideraremos primeiro a reprodução
assexuada . Acontece assim: uma cópia de todos os genes do agente é feita, um dos vários tipos de mudanças é feito sobre eles -
mutações . Em nossa versão do NEAT, as seguintes mutações são possíveis:
- mudança de peso da conexão
- desvincular
- adicionar link
- inserção de neurônios.
Os três primeiros tipos de mutações são simples e compreensíveis, sem maiores explicações. A inserção do neurônio é mostrada na figura abaixo, sempre ocorre no lugar da conexão existente, a conexão é removida e dois novos aparecem em seu lugar:
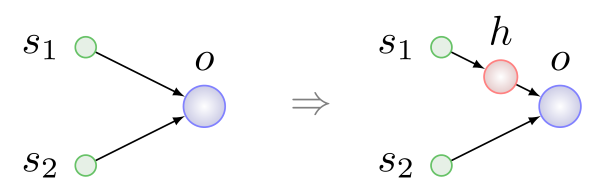
Aqui h é
um neurônio
oculto .
Dois agentes estão envolvidos na reprodução sexual ou
cruzamento - pais e, como resultado, um terceiro aparece - uma criança. No processo de formação do genótipo da criança, ocorre uma troca, digamos, de genes ou grupos de genes de pais
com significado idêntico. O segundo princípio é exatamente o que você precisa para procurar genes com o mesmo significado.
Imagine que queremos agentes cruzados com genótipos que sofreram diferentes séries de mutações da lista acima:
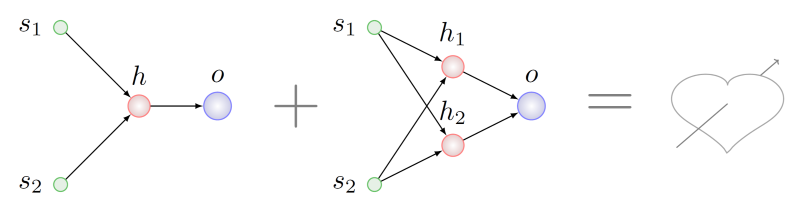
Parece lógico procurar alguns fragmentos comuns em termos de topologia em ambos os pais e pegar um pedaço desses fragmentos para o genótipo do feto. Será difícil fazer isso, mesmo
NP é difícil no caso geral, mas suponha que tenhamos conseguido. Nesse caso, descobrimos que no pai à direita existem dois subgráficos isomórficos ao gráfico do pai à esquerda. Na figura abaixo, os arcos desses subgráficos são destacados em cores diferentes:
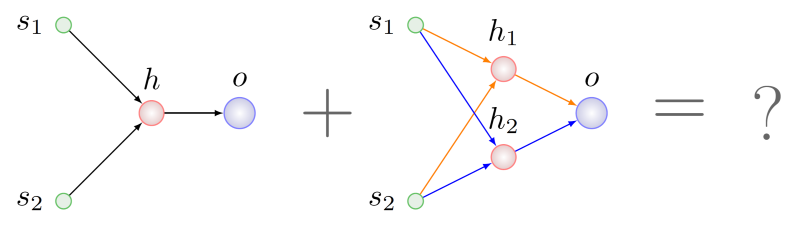
Qual escolher para recombinação com genes parentais esquerdos?
Vamos voltar à história do surgimento desses genótipos:
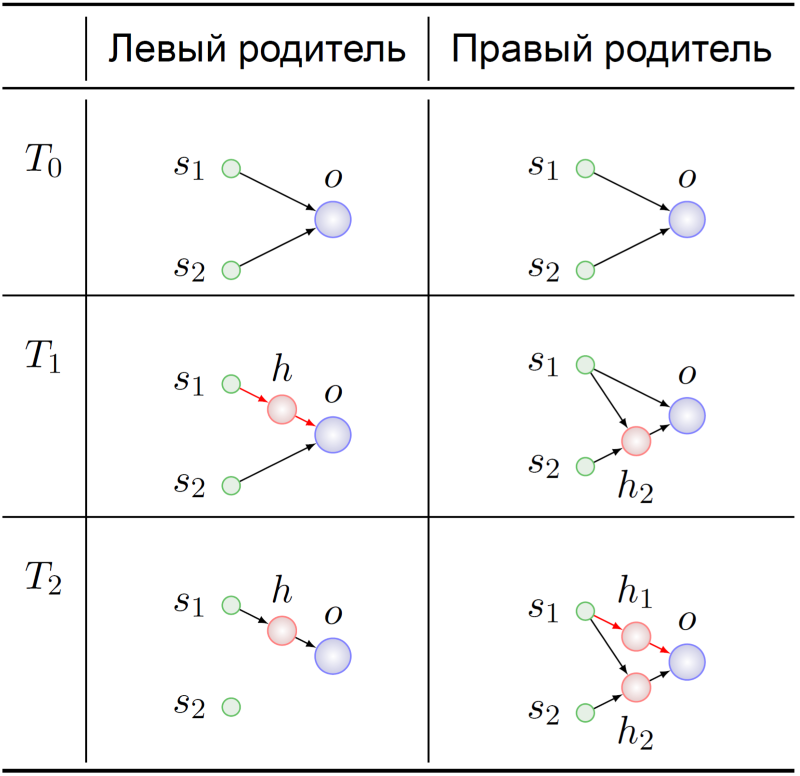
Ambos os ancestrais dos agentes pais começaram, como esperado, com NS mínimo (T
0 ). Seus genomas de alguma forma se modificaram ali e, no momento T
1 , o neurônio oculto foi inserido na conexão s -> o no ancestral do pai esquerdo. Nesse momento dramático, os genes que codificam as ligações s
1 -> heh -> o encontram seu significado no ancestral do pai esquerdo:
substituição do link s 1 -> o .
Os genes s
1 -> h
1 e h
1 -> o no genótipo do pai certo no momento T2 têm exatamente o mesmo significado. O destino adicional de nossos antepassados não é de particular interesse para nós - já sabemos com o que misturar:
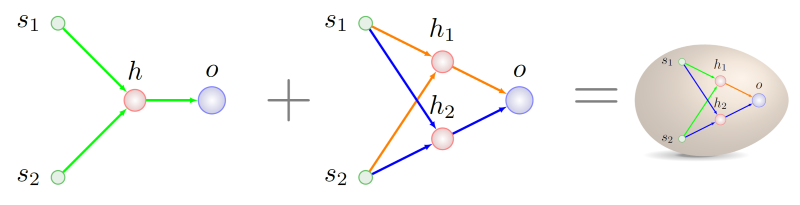
Como escrever a história genética corretamente, será possível decifrar da próxima vez, principalmente porque temos alguns achados nessa área, eles estão associados à adaptação da técnica original a um esquema de reprodução estável.
É hora de terminar. O artigo começou com o Youtube - e nós o concluiremos. Em uma versão anterior do simulador, um colega que escreveu o código para gerar a faixa terminou com nada, um abismo sem fundo. A reação de uma rede neural que evoluiu por muito tempo na presença de um firmamento terrestre sob rodas para um projeto desse pequeno universo talvez possa ser chamada de "quebra de modelo":
Uma extensa coleção de outras histórias anedóticas da vida de cibernaturalistas pode ser encontrada em
[3] .
Fontes
[1] KO Stanley e R .. Miikkulainen, Evoluindo Redes Neurais através de Topologias Aumentadas Evolutionary Computation, vol. 10, n. 2, pp. 99-127, 2002.
[2] C. Green, “Uma revisão das funções de ativação no SharpNEAT”, 19 de junho de 2017.[3] J. Lehman et al, “A Criatividade Surpreendente da Evolução Digital: Uma Coleção de Anedotas das Comunidades de Pesquisa em Computação Evolutiva e Vida Artificial”, arXiv: Computação Neural e Evolutiva, 2018.