Como o LIGO pode ver ondas gravitacionais se a luz do GRT se estender junto com o espaço?

Como o LIGO pode detectar ondas gravitacionais se elas esticam a luz junto com o espaço entre os espelhos?

Crédito da imagem: www.ligo.caltech.edu

Esta questão certamente surge quando a conversa se refere à detecção de ondas gravitacionais (GW). Normalmente, o argumento é o seguinte: sabemos que existe um desvio para o vermelho gravitacional , ou seja, a gravidade estica os comprimentos de onda. É razoável supor que no LIGO a luz também se estenda, e os comprimentos de onda que usamos como uma “régua” para medir a distância entre os espelhos se estendam na mesma extensão que a própria distância. Então, como alguém pode usar um interferômetro para medir ondas gravitacionais?

Imagine possíveis respostas para isso:

1. GV não afeta a luz, então a questão não faz sentido.
2. Os GWs esticam o comprimento de onda da luz, mas muito fracamente, por isso não percebemos.
3. Não importa, o princípio de detecção não é sensível ao comprimento de onda.
4. Detectores realmente não funcionam.

1. Havia um menino?

Para começar, os detectores ainda funcionam.


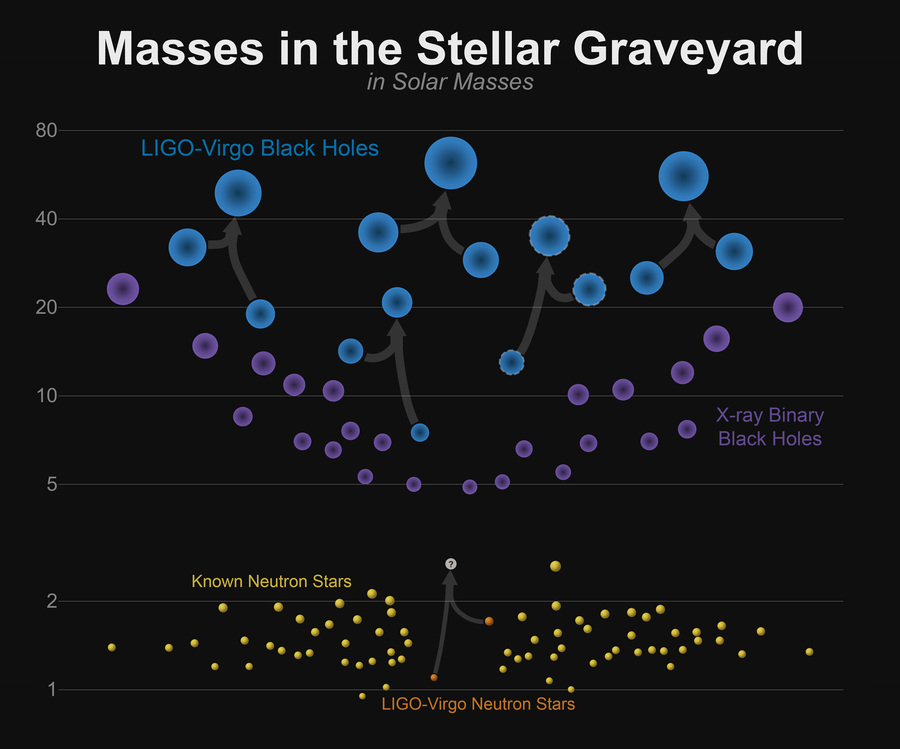Cemitério de estrelas: massas de estrelas de nêutrons e buracos negros conhecidos por nós, incluindo observações do LIGO. Crédito da imagem: www.ligo.caltech.edu


No momento, vimos mais de uma dúzia de eventos do GW. O mais convincente é a detecção conjunta de GW e flashes de luz da fusão de estrelas de nêutrons. No LIGO, eles viram o GW, triangularam a área no céu, de onde eles vieram, e disseram aos telescópios: "Olhe lá!" Eles olharam e viram o surto do kilon exatamente onde indicado pelo LIGO. Portanto, há pouca dúvida de que funciona. Vamos ver exatamente.

2. O que é o LIGO em geral?

O detector Virgo é um detector europeu, um dos três detectores que viram ondas gravitacionais. Crédito da imagem: www.ligo.caltech.edu

Uma onda gravitacional, que surge durante a fusão de objetos maciços (por exemplo, dois buracos negros), se propaga no espaço-tempo como uma pequena perturbação de sua curvatura. Isso leva ao fato de que as distâncias entre os objetos mudam levemente quando a onda passa através deles (mais precisamente, a própria definição de distância muda). No LIGO, os dois braços de um interferômetro Michelson de 4 km mudam de ~ 10 a ¹⁸ m, e o detector é capaz de detectar essa alteração. Um ponto importante: se o guia de ondas esticar um braço do interferômetro, o segundo braço será compactado proporcionalmente (idealmente, isso decorre da natureza quadrupolo do guia de ondas e da presença de duas polarizações).

Já existe um bom artigo sobre Habré sobre o dispositivo LIGO , então vamos à resposta à pergunta feita no início do artigo.

3. Conceito de medição

Uma animação que demonstra como o detector funciona

Para começar, considere um exemplo que o ajudará a entender o princípio básico do detector.
Este detector trabalha com luz contínua - o laser bombeia constantemente os ressonadores no LIGO com luz e os fotodiodos detectam constantemente a presença / ausência de um sinal. Mas, por exemplo, vamos simplificar o esquema: suponha que tenhamos uma fonte de fótons que envia fótons simultaneamente em duas direções, onde são refletidos pelos espelhos e retornados ao detector de fótons (no nosso caso, o divisor de feixe), como mostra a ilustração abaixo.



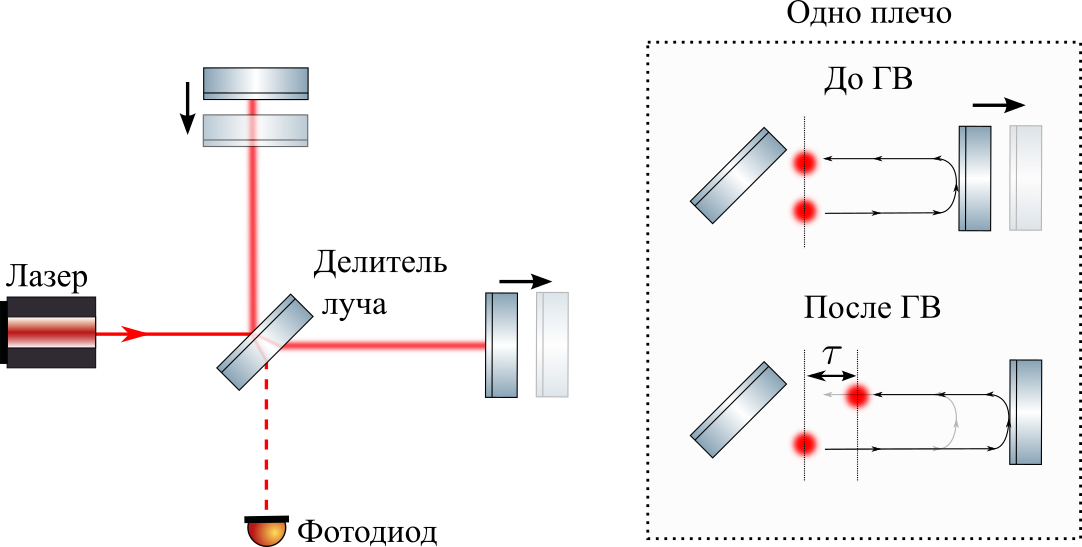
Se dois espelhos estiverem a uma distância igual da fonte de fótons, dois fótons retornarão ao detector ao mesmo tempo (como na figura acima). Se GW esticar um ombro em $$$x$ e comprime outro em $$$x$ então um fóton chegará mais cedo que outro em $$$2 \ tau = 4x / c \ sim 4 \ vezes 10 ^ {- 18} / (3 * 10 ^ 8) \ sim 10 ^ {- 26}$ c, como na figura acima. Isso é muito pequeno, é claro, e seria impossível medir diretamente, mas medimos um pouco diferente. Eu só queria demonstrar a principal mensagem deste post:

O detector não é uma régua, mas um relógio

4. Explicação detalhada

Vamos agora considerar o interferômetro Michelson, no qual brilham com um laser contínuo, o feixe é dividido igualmente no divisor de feixes, refletido nos espelhos finais e, retornando ao divisor de feixes, interfere.



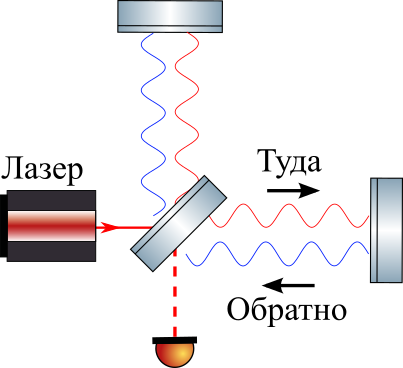
Para simplificar, assumimos que o GW é um "passo" - ele muda instantaneamente a métrica em uma pequena quantidade $$$h_0$ . Com as palavras "mudança métrica", queremos dizer que a definição de distância muda um pouco, ou seja, todas as distâncias aumentam (ou diminuem) em $$$(1+ h_0 / 2)$ vezes. Se considerarmos a distância entre o divisor de feixe e o espelho final $$$L$ , quando a métrica for alterada, aumentará em $$$\ Delta L$ para que $$$h_0 = 2 \ Delta L / L$ .

Nota: é importante que a representação do GW como um “passo” seja útil apenas para consideração nos dedos, na realidade é necessário considerar o GW como uma onda com um determinado comprimento.

Considere o que acontece com a luz neste momento.


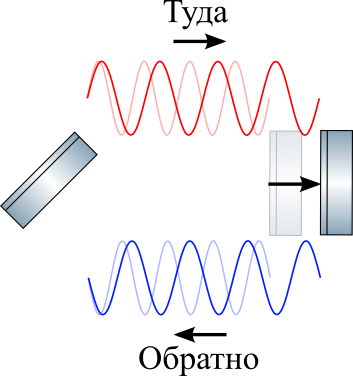No momento da chegada do GW, o comprimento de onda da luz é esticado em relação ao comprimento de onda original (curvas translúcidas). NB: o comprimento de onda mostrado é comparável ao comprimento do ombro para maior clareza; na verdade, o comprimento de onda do laser é de cerca de 1 mícron e o comprimento do ombro é de 4 km.

Se o espelho tiver um nó de onda estacionária antes do alongamento, ele permanecerá lá após o alongamento, conforme mostrado na figura acima. Porque Isso é exigido pela teoria da relatividade: como não existe um sistema de repouso independente e independente, o nó não tem nada a fazer senão ficar onde estava em relação à superfície do espelho. Ou seja, o comprimento de onda aumenta em $$$(1 + h_0 / 2)$ vezes, como esperado no início do artigo, por analogia com o desvio para o vermelho gravitacional.

Então acontece que, mesmo assim, a luz foi esticada junto com o detector, e não conseguimos registrar o sinal?

E ainda podemos!



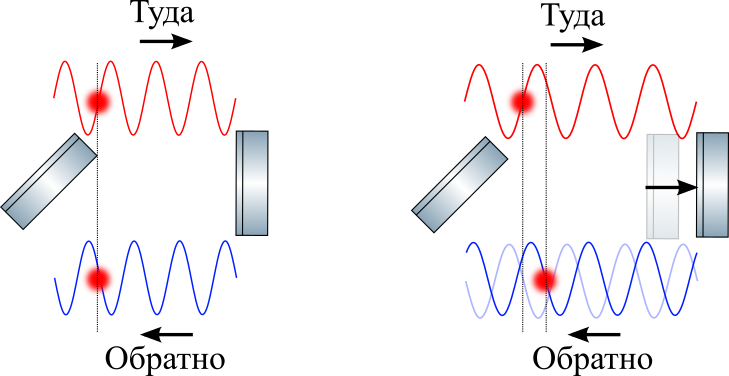
Mostraremos isso na figura acima: traçaremos o caminho de um nó específico em uma onda esticada no caminho para lá e para trás, marcando-o com um círculo. Apesar do alongamento, a luz ainda se propaga à velocidade da luz. Isso significa que, para a parte da onda que acabou de entrar no ombro, levará mais tempo para superar a viagem de ida e volta (lembre-se aqui do parágrafo 3 do artigo). Ou seja, sua fase na chegada mudará (como pode ser visto na figura).

Além disso, a luz continua a bombear luz com um comprimento de onda não esticado.

A fase acumulada pela luz no caminho do divisor para o espelho e vice-versa depende da frequência natural da luz $$$\ omega _ {\ rm soluço}$ observado no divisor de feixe e tempo $$$\ tau _ {\ rm ida e volta}$ :

$$

$$\ phi = \ omega _ {\ rm soluço} \ tau _ {\ rm ida e volta}$$

Pode-se mostrar (por exemplo, aqui ou aqui ) que, se o comprimento de onda do HW for muito maior que o comprimento do braço do interferômetro, a frequência natural praticamente não muda. E o tempo de atraso dependerá da distância entre os espelhos:

$$

$$\ tau _ {\ rm ida e volta} \ approx \ frac {2 L} {c} (1+ \ frac {h_0} {2})$$

Assim, na chegada do divisor de feixe, a fase da luz terá um atraso, dependendo do tamanho da métrica $$$h_0$ . Por outro lado, tudo acontecerá da mesma forma, com precisão na placa à frente $$$h_0$ - porque este ombro não será esticado, mas comprimido. Como resultado, no divisor de feixe, a diferença de fase entre os dois ombros será

$$

$$\ Delta \ phi = \ frac {2 \ omega L} {c} (1+ \ frac {h_0} {2}) - \ frac {2 \ omega L} {c} (1- \ frac {h_0} { 2}) = 2 \ pi \ frac {L} {\ lambda} h_0$$

A partir desta equação, a propósito, é óbvio por que o detector tem um braço tão longo - quanto maior o comprimento L em comparação com o comprimento de onda, mais sensível o detector. Os detectores de última geração, como o Telescópio Einstein ou o Cosmic Explorer , serão ainda mais longos - de 10 a 40 km.

Observo que, na realidade, o GW não é um "passo", é uma onda com comprimento de onda muito maior que o comprimento do ombro; portanto, durante o alongamento, um "nó" da onda de luz passa para frente e para trás, seu alongamento pode ser negligenciado. Portanto, o primeiro momento de "esticar" a luz a partir da consideração "nos dedos" está praticamente ausente.

Então, a conclusão. A resposta correta para a pergunta está no começo do artigo: as ondas 2 e 3 - gravitacionais agem na luz de maneira um pouco diferente da distância entre os espelhos, mas isso não importa, pois em qualquer caso medimos não o comprimento de onda, mas o atraso de fase. Em outras palavras

O detector de ondas gravitacionais funciona como um relógio, não como uma régua.

5. Conclusão

É importante enfatizar que a onda gravitacional afeta o comprimento de onda da luz de maneira diferente da distância entre os espelhos. Isso se deve principalmente ao fato de o período do GW ser muito maior do que o tempo necessário para a luz ir e voltar. O braço do interferômetro continua a se esticar ao longo do tempo, após o período do GW, e a luz está constantemente saindo "nova" do laser.

Além disso, o detector real possui espelhos adicionais que criam vários ressonadores, o que aumenta efetivamente o comprimento do ombro. No entanto, isso não afeta a idéia principal.

Assim, podemos realmente observar ondas gravitacionais e nenhuma teoria da conspiração!

Crédito da imagem: www.ligo.caltech.edu

6. Notícias LIGO

Como um postscript, um pouco sobre o que está acontecendo no LIGO agora. O segundo ciclo de observações de O2 trouxe não apenas a observação da fusão de estrelas de nêutrons e a primeira observação conjunta de HS por três detectores , incluindo Virgo, mas também muitos outros eventos. Em um futuro próximo, os resultados da análise de dados serão publicados e os próprios dados estarão abertos e disponíveis para análise.

O LIGO agora está concluindo inúmeras atualizações, incluindo a instalação de luz compactada e um laser mais poderoso, o que aumentará a sensibilidade do detector várias vezes e permitirá que você observe muito mais eventos (em um bom cenário - por evento por semana).

No início do próximo ano, um novo ciclo de observação da O3 começará.