Laplace Blur - É possível blub Laplace em vez de Gauss, quantas vezes é mais rápido e vale a pena a perda da precisão de 1/32

"Desfocar" nas pessoas comuns é um efeito de desfoque no processamento de imagens digitais. Pode ser muito eficaz em si mesmo e como um componente de animações de interface ou efeitos derivados mais complexos (bloom / focusBlur / motionBlur). Com tudo isso, o blues honesto na testa é bastante lento. E frequentemente as implementações incorporadas na plataforma de destino deixam muito a desejar. Ou a velocidade é triste, os artefatos machucam os olhos. A situação gera muitas implementações de compromisso que são melhores ou piores para determinadas condições. Uma implementação original com boa qualidade de confiabilidade e velocidade mais alta, enquanto a menor dependência de hardware está esperando por você. Bom apetite!

(Laplace Blur - Nome proposto do algoritmo original)

Hoje, minha demonstração interna me chutou e me forçou a escrever um artigo que tinha que ser escrito seis meses atrás. Como amador, no lazer, para desenvolver algoritmos de efeitos originais, eu gostaria de oferecer ao público um algoritmo "quase azul gausiano", caracterizado pelo uso de instruções de processador excepcionalmente rápidas (turnos e máscaras) e, portanto, acessíveis à implementação de microcontroladores (extremamente rápido em um ambiente limitado).

De acordo com minha tradição de escrever artigos sobre o Habr, darei exemplos em JS como a linguagem mais popular e, acredite ou não, é muito conveniente para fins de prototipagem rápida de algoritmos. Além disso, a capacidade de implementar isso efetivamente no JS veio com matrizes digitadas. No meu laptop não muito potente, a imagem em tela cheia é processada a uma velocidade de 30 fps (não há multithreading de trabalhadores).


Esta descrição está presente aqui, em vez de explicar o curso de meus pensamentos e conjecturas que me levaram ao resultado. Para quem estiver interessado:

Função Gauss original:



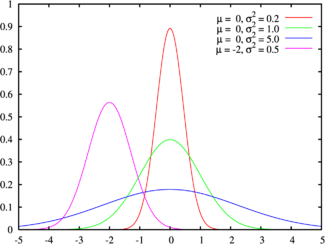
g (x) = a * e ** (- ((xb) ** 2) / c), em que
a é a amplitude (se tivermos oito bits de cor por canal, então = 256)
e é a constante de Euler ~ 2,7
b - deslocamento do gráfico em x (não precisamos = 0)
c - parâmetro que afeta a largura do gráfico associado a ele como ~ w / 2,35

Nossa função privada (menos o expoente removido com a substituição da multiplicação por divisão):



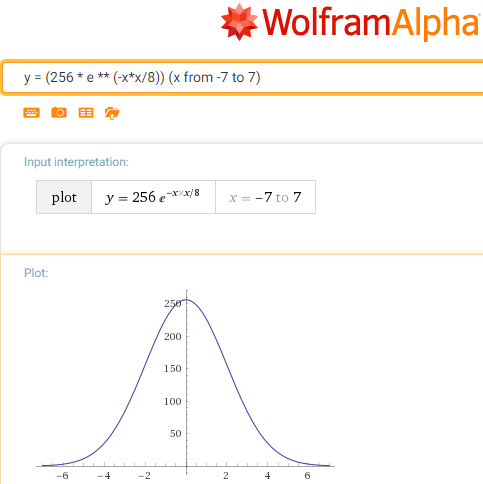
g (x) = 256 / e ** (x * x / c)

Deixe a ação de aproximação suja começar:
Observe que o parâmetro c está muito próximo da meia largura e define 8 (isso ocorre devido a quantas etapas você pode mudar um canal de 8 bits cada).

Também substituímos e por 2, no entanto, observando que isso afeta mais a curvatura do “sino” do que suas bordas. Na verdade, afeta 2 / e vezes, mas a surpresa é que esse erro compensa o parâmetro c, para que as condições de contorno ainda estejam em ordem e o erro apareça apenas em uma "distribuição normal" ligeiramente incorreta, para gráficos algoritmos, isso afetará a dinâmica das transições de cores gradientes, mas é quase impossível perceber com os olhos.

Então agora nossa função é a seguinte:
gg (x) = 256/2 ** (x * x / 8) ou gg (x) = 2 ** (8 - x * x / 8)
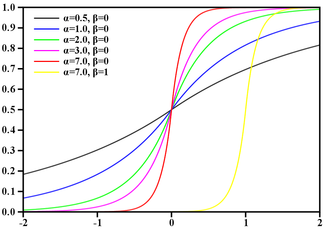
Observe que o expoente (x * x / 8) tem o mesmo intervalo de valor [0-8] que a função de um abs de ordem inferior (x); portanto, este último é candidato a substituição. Vamos verificar rapidamente o palpite, observando como o gráfico muda com ele gg (x) = 256 / (2 ** abs (x)):

GaussBlur vs LaplasBlur:



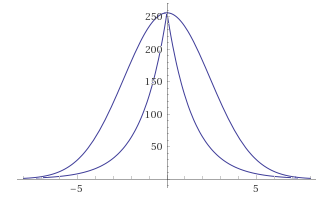
Os desvios parecem ser muito grandes; além disso, a função, tendo perdido sua suavidade, agora tem um pico. Mas ei.

Primeiro, não vamos esquecer que a suavidade dos gradientes obtidos pelo desfoque não depende da função de densidade de probabilidade (que é a função de Gauss), mas de sua integral - a função de distribuição. Naquela época, eu não conhecia esse fato, mas, de fato, tendo realizado uma aproximação "destrutiva" em relação à função de densidade de probabilidade (Gauss), a função de distribuição permaneceu bastante semelhante.

Foi:



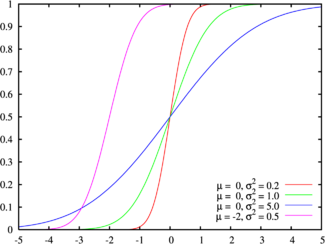
Tornou-se:



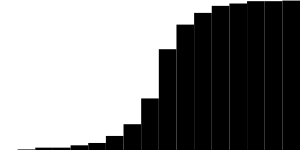
A prova, tirada do algoritmo pronto, coincide:



No futuro, direi que o erro de desfoque do meu algoritmo em relação ao Gausian x5 foi de apenas 3%.

Portanto, chegamos muito mais perto da função de distribuição de Laplace. Quem teria pensado, mas eles podem lavar as imagens 97% não é pior.

Prova, diferenças blura gausiana x5 e "Laplace blura" x7:



(esta não é uma imagem em preto! Você pode estudar no editor)

A suposição dessa transformação nos permitiu avançar para a idéia de obter o valor por filtragem iterativa, à qual planejei reduzir inicialmente.

Antes de contar um algoritmo específico, será honesto se eu me antecipar e descrever imediatamente sua única desvantagem (embora a implementação possa ser corrigida com uma perda de velocidade). Mas esse algoritmo é implementado usando aritmética de cisalhamento, e potências de 2 são sua limitação. Portanto, o original é feito para desfocar x7 (o que nos testes é o mais próximo a Gausian x5). Essa limitação da implementação está relacionada ao fato de que, com uma cor de oito bits, alterando o valor na unidade de filtro em um bit por etapa, qualquer efeito do ponto termina em no máximo 8 etapas. Também implementei uma versão um pouco mais lenta por meio de proporções e adições adicionais, que implementam uma divisão rápida por 1,5 (resultando em um raio de x15). Porém, com a aplicação posterior dessa abordagem, o erro aumenta e a velocidade diminui, o que não permite que ela seja usada dessa maneira. Por outro lado, vale ressaltar que x15 já é suficiente para não notar a diferença, o resultado é obtido a partir do original ou da imagem amostrada em baixa. Portanto, o método é bastante adequado se você precisar de uma velocidade extraordinária em um ambiente limitado.

Portanto, o núcleo do algoritmo é simples, são executadas quatro passagens do mesmo tipo:

1. Metade do valor da unidade t (inicialmente igual a zero) é adicionada à metade do valor do próximo pixel, o resultado é atribuído a ele. Continue desta maneira até o final da linha da imagem. Para todas as linhas.

Após a conclusão da primeira passagem, a imagem é desfocada em uma direção.

2. Na segunda passagem, fazemos o mesmo na direção oposta para todas as linhas.
Temos uma imagem que está completamente desfocada horizontalmente.

3-4. Agora faça a mesma coisa verticalmente.
Feito!

Inicialmente, usei um algoritmo de duas passagens com a implementação de back-blur através da pilha, mas é difícil de entender, não gracioso, e acabou sendo mais lento nas arquiteturas atuais. Talvez o algoritmo de uma passagem seja mais rápido nos microcontroladores, além da capacidade de produzir o resultado progressivamente também será um plus.

O atual método de implementação em quatro direções, olhei para Habré do guru anterior sobre algoritmos de desfoque. habr.com/post/151157 Aproveito esta oportunidade para expressar minha solidariedade e profunda gratidão a ele.

Mas os hacks não terminaram aí. Agora, sobre como calcular os três canais de cores em uma instrução de processador! O fato é que o deslocamento de bits usado como divisão por dois permite controlar muito bem a posição dos bits resultantes. O único problema é que os bits mais baixos dos canais deslizam para os mais próximos, mas você pode simplesmente redefini-los, resolver o problema com alguma perda de precisão. E, de acordo com a fórmula de filtro descrita, a adição de metade do valor da unidade com metade do valor da próxima célula (sujeito à redefinição dos bits descarregados) nunca leva ao estouro, portanto, não se preocupe. E a fórmula do filtro para o cálculo simultâneo de todos os dígitos passa a ser a seguinte:

buf32 [i] = t = (((t >> 1) & 0x7F7F7F) + ((buf32 [i] >> 1) & 0x7F7F7F);

No entanto, é necessário mais um acréscimo: verificou-se experimentalmente que a perda de precisão nesta fórmula é muito significativa, o brilho da imagem aumenta visualmente significativamente. Tornou-se claro que o bit perdido precisa ser arredondado para o todo mais próximo e não descartado. Uma maneira fácil de fazer isso na aritmética inteira é adicionar metade do divisor antes da divisão. Nosso divisor é dois, então você precisa adicionar um, em todos os dígitos, - a constante 0x010101. Mas com qualquer adição, é preciso ter cuidado com o excesso. Portanto, não podemos usar essa correção para calcular metade do valor da próxima célula. (Se houver cor branca, o excesso será excedido e, portanto, não a corrigiremos). Mas aconteceu que o principal erro foi cometido pela divisão múltipla da unidade, que podemos corrigir. Porque, de fato, mesmo com essa correção, o valor no inversor não aumentará acima de 254. Mas, quando adicionado a 0x010101, o estouro não será garantido. E a fórmula do filtro com correção assume a forma:

buf32 [i] = t = (((((0x010101 + t) >> 1) & 0x7F7F7F) + ((buf32 [i] >> 1) & 0x7F7F7F);

De fato, a fórmula executa a correção muito bem; portanto, quando você aplica repetidamente esse algoritmo à imagem, os artefatos começam a ficar visíveis apenas nas dez últimas passagens. (não o fato de que repetir a blura gausiana não produzirá esses artefatos).

Além disso, há uma propriedade maravilhosa com muitos passes. (Isso não se deve ao meu algoritmo, mas à "normalidade" da distribuição normal). Já na segunda passagem do Laplace Blura, a função de densidade de probabilidade (se eu entendi tudo certo) será mais ou menos assim:



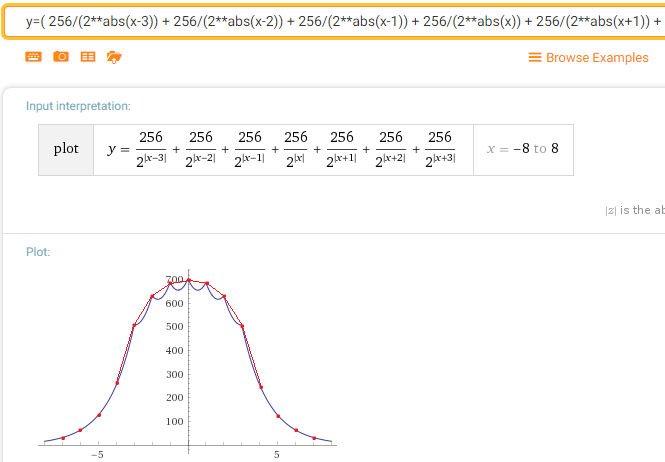
O qual, você vê, já está muito próximo do gaussiano.

Empiricamente, descobri que o uso de modificações com um raio grande é permitido em pares, porque a propriedade descrita acima compensa erros se a última passagem for mais precisa (o mais preciso é o algoritmo de desfoque x7 descrito aqui).

demonstração
rap
codpen

Um apelo para matemáticos legais:
O que seria interessante saber como é correto usar esse filtro separadamente, não tenho certeza se existe uma imagem de distribuição simétrica. Embora a heterogeneidade do olho não seja visível.

upd: Aqui levantarei links úteis, gentilmente apresentados por comentaristas e encontrados em outros khabrovitas.
1. Como os mestres da intel funcionam, contando com o poder do SSE - software.intel.com/en-us/articles/iir-gaussian-blur-filter-implementation-using-intel-advanced-vector-extensions (obrigado vladimirovich )
2. Base teórica sobre o tópico “Convoluções rápidas de imagens” + algumas de suas aplicações personalizadas em relação ao blues gaussiano honesto - blog.ivank.net/fastest-gaussian-blur.html (obrigado Grox )

Sugestões, comentários, críticas construtivas são bem-vindas!