Verificação numérica da hipótese abc (sim, essa)

Oi Habr.

Já existem vários artigos sobre a hipótese abc no Geektimes Habr (por exemplo, em 2013 e 2018 ). A própria história sobre um teorema que, a princípio, não pode ser provado por muitos anos, e depois não pode ser verificado pelo mesmo número de anos, certamente merece pelo menos um longa-metragem. Mas, à sombra dessa história maravilhosa, o próprio teorema é considerado superficialmente demais, embora não seja menos interessante. Já pelo menos pelo fato de a hipótese abc ser um dos poucos problemas não resolvidos da ciência moderna, a afirmação do problema que até um aluno do quinto ano pode entender. Se essa hipótese é realmente verdadeira, ela segue facilmente a prova de outros teoremas importantes, por exemplo, a prova do teorema de Fermat .

Sem reivindicar louros do Motizuki, também decidi tentar e verificar com um computador o quanto a igualdade prometida na hipótese é cumprida. Na verdade, por que não - os processadores modernos não servem apenas para jogar - por que não usar um computador para seu principal objetivo (computação) ...

Quem se importa com o que aconteceu, por favor, debaixo do gato.

Declaração do problema

Vamos começar do começo. Sobre o que é o teorema? Como a Wikipedia diz (a redação na versão em inglês é um pouco mais clara), para números mutuamente primos (sem divisores comuns) a, bec tais que a + b = c, para qualquer ε> 0, há um número limitado de triplos a + b = c, de modo que:



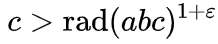
A função rad é chamada de radical e denota o produto dos fatores primos de um número. Por exemplo, rad (16) = rad (2 * 2 * 2 * 2) = 2, rad (17) = 17 (17 é primo), rad (18) = rad (2 * 3 * 3) = 2 * 3 = 6, rad (1.000.000) = rad (2 ^ 6 ⋅ 5 ^ 6) = 2 * 5 = 10.

Na verdade, a essência do teorema é que o número desses triplos é bastante pequeno. Por exemplo, se tomarmos aleatoriamente ε = 0,2 e a igualdade 100 + 27 = 127: rad (100) = rad (2 * 2 * 5 * 5) = 10, rad (27) = rad (3 * 3 * 3) = 3, rad (127) = 127, rad (a * b * c) = rad (a) * rad (b) * rad (c) = 3810, 3810 ^ 1,2 é claramente maior que 127, a desigualdade não é válida. Mas há exceções, por exemplo, para a igualdade 49 + 576 = 625, a condição do teorema é cumprida (aqueles que desejam podem verificar por conta própria).

O próximo momento chave para nós é um número limitado dessas igualdades, de acordo com o teorema. I.e. isso significa que você pode simplesmente tentar classificá-las em um computador. Como resultado, isso nos dá o Prêmio Nobel uma tarefa de programação bastante interessante.

Então, vamos começar.

Código fonte

A primeira versão foi escrita em Python e, embora essa linguagem seja muito lenta para esses cálculos, escrever código nela é fácil e simples, o que é conveniente para a criação de protótipos.

Obtendo o radical : decompomos o número em fatores primos, depois removemos as repetições, convertendo o array em um conjunto. Então é só pegar o produto de todos os elementos.

def prime_factors(n): factors = [] # Print the number of two's that divide n while n % 2 == 0: factors.append(int(2)) n = n / 2 # n must be odd at this point so a skip of 2 ( i = i + 2) can be used for i in range(3, int(math.sqrt(n)) + 1, 2): # while i divides n , print i ad divide n while n % i == 0: factors.append(int(i)) n = n / i # Condition if n is a prime number greater than 2 if n > 2: factors.append(int(n)) return set(factors) def rad(n): result = 1 for num in prime_factors(n): result *= num return result 

Números mutuamente primos : fatore os números e verifique a interseção dos conjuntos.

 def not_mutual_primes(a,b,c): fa, fb, fc = prime_factors(a), prime_factors(b), prime_factors(c) return len(fa.intersection(fb)) == 0 and len(fa.intersection(fc)) == 0 and len(fb.intersection(fc)) == 0 

Confira : usamos funções já criadas, tudo é simples aqui.

 def check(a,b,c): S = 1.2 # Eps=0.2 if c > (rad(a)*rad(b)*rad(c))**S and not_mutual_primes(a, b, c): print("{} + {} = {} - PASSED".format(a, b, c)) else: print("{} + {} = {} - FAILED".format(a, b, c)) check(10, 17, 27) check(49, 576, 625) 

Aqueles que desejam podem experimentar independentemente, copiando o código acima em qualquer editor de linguagem Python online. Obviamente, o código é executado conforme o esperado e enumerar todos os triplos para pelo menos um milhão seria muito longo. Abaixo do spoiler, há uma versão otimizada, é recomendável usá-lo.

A versão final foi reescrita em C ++ usando multithreading e alguma otimização (trabalhar em C com conjuntos que se cruzam seria muito grave, embora provavelmente mais rápido). O código fonte está sob o spoiler, pode ser compilado no compilador g ++ gratuito, o código funciona no Windows, OSX e até no Raspberry Pi.


Para quem tem preguiça de instalar o compilador C ++, é fornecida uma versão Python levemente otimizada, que pode ser iniciada em qualquer editor online (usei https://repl.it/languages/python ).

Resultados

Os triplos a, b, c são realmente muito poucos.

Alguns resultados são apresentados abaixo:
N = 10 : 1 "três", lead time <0,001c
1 + 8 = 9

N = 100 : 2 "triplos", tempo de execução <0,001c
1 + 8 = 9
1 + 80 = 81

N = 1000 : 8 "triplica", tempo de execução <0,01c
1 + 8 = 9
1 + 80 = 81
1 + 242 = 243
1 + 288 = 289
1 + 512 = 513
3 + 125 = 128
13 + 243 = 256
49 + 576 = 625

N = 10000 : 23 "triplica", tempo de execução 2s


N = 100000 : 53 triplos, tempo de execução 50c


Com N = 1.000.000, temos apenas 102 "triplos", uma lista completa é fornecida sob o spoiler.


Infelizmente, o programa ainda funciona devagar, não esperei resultados para N = 10.000.000, o tempo de cálculo é superior a uma hora (talvez eu tenha cometido um erro ao otimizar o algoritmo em algum lugar, e posso fazer melhor).

Ainda mais interessante para ver os resultados graficamente:



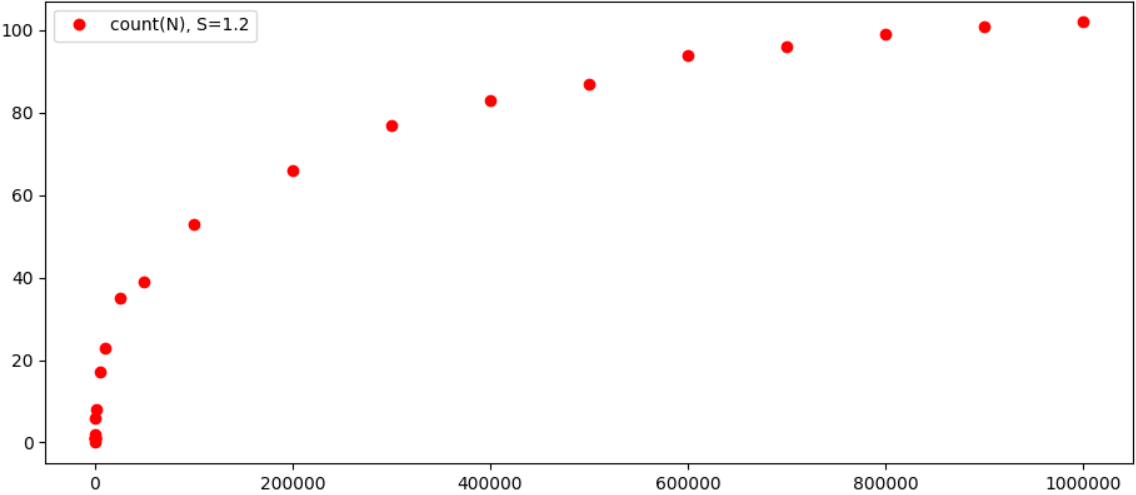
Em princípio, é bastante óbvio que a dependência do número possível de triplos em N cresce notavelmente mais lenta que o próprio N, e é provável que o resultado converja para algum número específico para cada ε. A propósito, com um aumento em ε, o número de "triplos" diminui visivelmente, por exemplo, para ε = 0,4, temos apenas 2 igualdades para N <100000 (1 + 4374 = 4375 e 343 + 59049 = 59392). Então, em geral, parece que o teorema realmente se mantém (bem, e provavelmente já foi testado em computadores mais poderosos, e talvez tudo isso tenha sido calculado há muito tempo).

Aqueles que desejam podem experimentar por conta própria, se alguém tiver resultados para números 10.000.000 e superiores, terei o prazer de adicioná-los ao artigo. Obviamente, seria interessante “contar” até o momento em que o conjunto de “triplos” parar completamente de crescer, mas pode levar um tempo muito longo, a velocidade de cálculo parece depender de N como N * N (ou talvez N ^ 3) e do processo muito longo No entanto, algo incrível está por perto, e aqueles que desejam podem muito bem participar da pesquisa.

Editar: conforme sugerido nos comentários, a Wikipedia já possui uma tabela com os resultados - no intervalo N até 10 ^ 18 o número de "triplos" ainda está crescendo, portanto o "fim" do conjunto ainda não foi encontrado. Ainda mais interessante - a intriga ainda é preservada.