Mais recentemente, tive que resolver outra tarefa trivial de treinamento do meu professor. No entanto, resolvendo isso, consegui chamar a atenção para coisas sobre as quais nunca havia pensado antes; talvez você também não tenha pensado nisso. É mais provável que este artigo seja útil para estudantes e para todos que iniciam sua jornada no mundo da programação paralela usando o MPI.

Nosso "dado:"
Portanto, a essência de nossa tarefa essencialmente computacional é comparar quantas vezes um programa que usa transferências ponto a ponto atrasadas e sem bloqueio é mais rápido do que aquele que usa transferências ponto a ponto de bloqueio. Realizaremos medições para matrizes de entrada das dimensões 64, 256, 1024, 4096, 8192, 16384, 65536, 262144, 1048576, 4194304, 16777216, 33554432 elementos. Por padrão, propõe-se resolvê-lo por quatro processos. E aqui, de fato, é o que consideraremos:
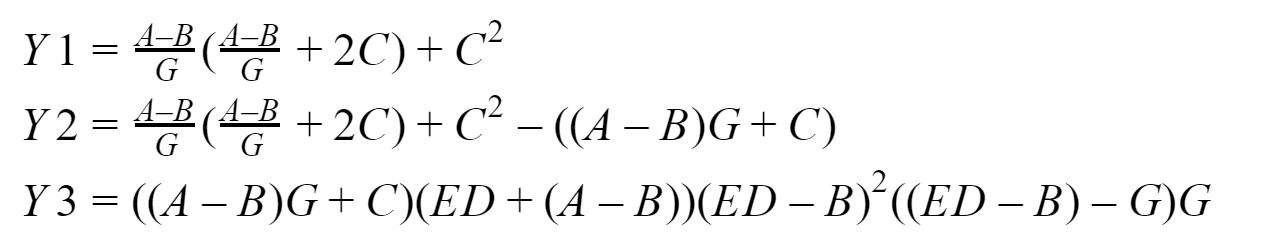
Na saída, devemos obter três vetores: Y1, Y2 e Y3, que o processo zero coletará. Vou testar tudo isso no meu sistema com base em
um processador Intel com 16 GB de RAM. Para desenvolver programas, usaremos a implementação do padrão
MPI da Microsoft versão 9.0.1 (no momento da redação deste documento, é relevante), o Visual Studio Community 2017 e não o Fortran.
Material
Eu não gostaria de descrever em detalhes como as funções MPI que serão usadas funcionam. Você sempre pode
consultar a documentação para isso , portanto, darei apenas uma breve visão geral do que usaremos.
Bloqueio de troca
Para bloquear mensagens ponto a ponto, usaremos as funções:MPI_Send - implementa o bloqueio do envio de mensagens, ou seja, depois de chamar a função, o processo é bloqueado até que os dados enviados sejam gravados da memória no buffer interno do sistema MPI, após o qual o processo continua a trabalhar mais;
MPI_Recv - executa o bloqueio da recepção de mensagens, ou seja, Após chamar a função, o processo é bloqueado até que os dados do processo de envio cheguem e até que esses dados sejam completamente gravados no buffer do processo de recebimento pelo ambiente MPI.
Troca não bloqueada diferida
Para mensagens ponto a ponto sem bloqueio adiadas, usaremos as funções:MPI_Send_init - em segundo plano prepara o ambiente para o envio de dados que ocorrerão em algum futuro e sem bloqueios;
MPI_Recv_init - esta função funciona de maneira semelhante à anterior, somente desta vez para receber dados;
MPI_Start - inicia o processo de recebimento ou transmissão de uma mensagem, também é executado em segundo plano de a.k.a. sem bloqueio;
MPI_Wait - é usado para verificar e, se necessário, aguardar a conclusão do envio ou recebimento de uma mensagem, mas apenas bloqueia o processo, se necessário (se os dados "não forem enviados" ou "não recebidos"). Por exemplo, um processo deseja usar dados que ainda não foram alcançados - nada bom, portanto, inserimos o MPI_Wait na frente do local em que esses dados serão necessários (os inserimos mesmo que exista apenas um risco de corrupção de dados). Outro exemplo: o processo iniciou a transferência de dados em segundo plano e, após iniciar a transferência, imediatamente começou a alterar esses dados de alguma forma - nada bom, então inserimos MPI_Wait na frente do local no programa em que começa a alterar esses dados (aqui também os inserimos, mesmo que existe simplesmente um risco de corrupção de dados).
Assim,
semanticamente ,
a sequência de chamadas com uma troca não bloqueada adiada é a seguinte:
- MPI_Send_init / MPI_Recv_init - preparando o ambiente para receber ou transmitir
- MPI_Start - inicia o processo de recebimento / transmissão
- MPI_Wait - corremos o risco de danos (incluindo "envio insuficiente" e "subnotificação") de dados transmitidos ou recebidos
Também usei
MPI_Startall ,
MPI_Waitall em meus programas de teste, o significado deles é basicamente o mesmo que MPI_Start e MPI_Wait, respectivamente, apenas eles operam em vários pacotes e / ou transmissões. Mas essa não é a lista completa das funções de início e espera, existem várias outras funções para verificar a conclusão das operações.
Arquitetura entre processos
Para maior clareza, construímos um gráfico para realizar cálculos por quatro processos. Nesse caso, deve-se tentar distribuir todas as operações aritméticas de vetor de maneira relativamente uniforme nos processos. Aqui está o que eu tenho:
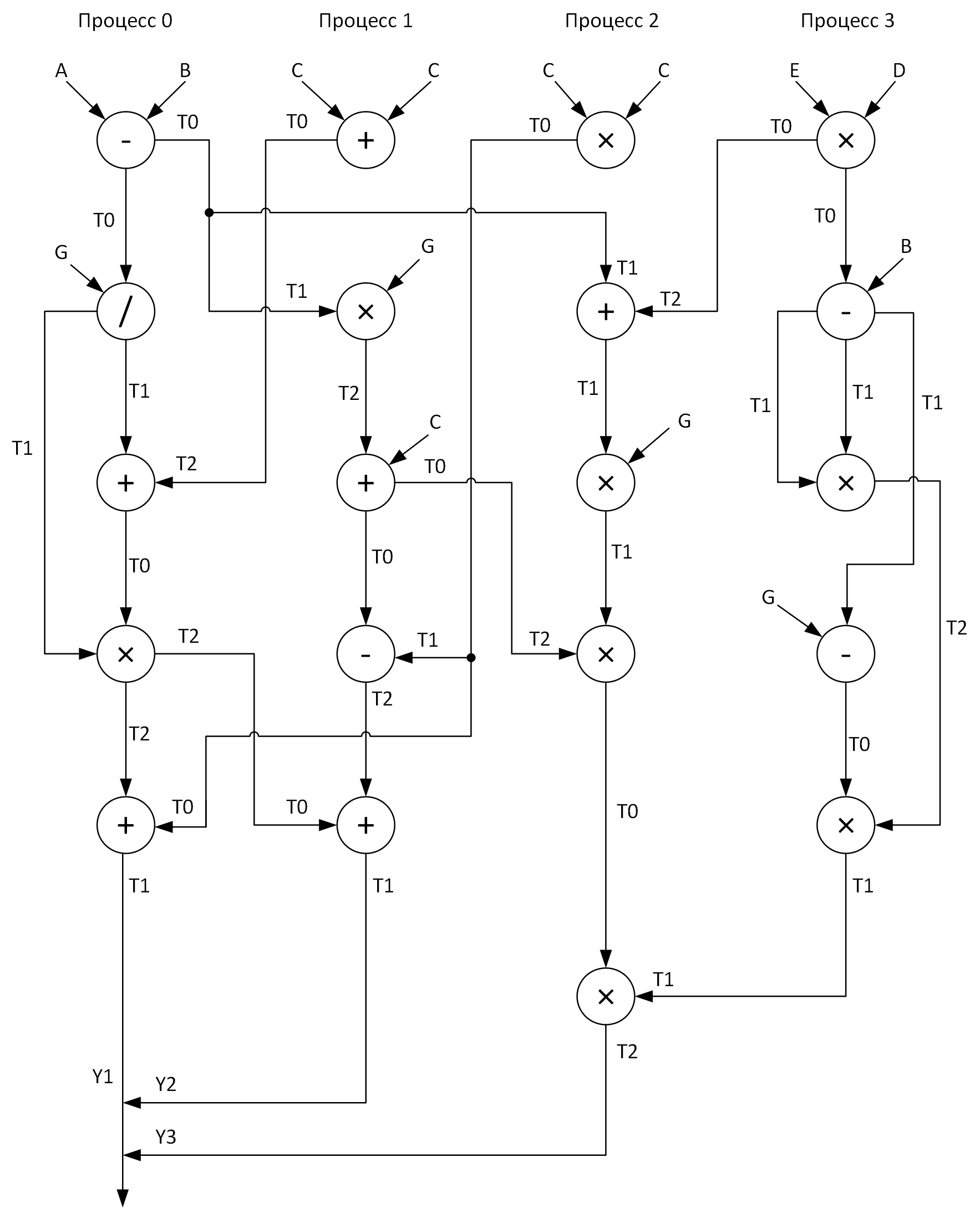
Veja essas matrizes T0-T2? Esses são buffers para armazenar resultados intermediários de operações. Além disso, no gráfico ao enviar mensagens de um processo para outro, no início da seta está o nome da matriz cujos dados são transmitidos e no final da seta está a matriz que recebe esses dados.
Bem, quando finalmente respondemos às perguntas:
- Que tipo de problema estamos resolvendo?
- Quais ferramentas usaremos para resolvê-lo?
- Como vamos resolver isso?
Resta apenas resolvê-lo ...
Nossa "solução:"
A seguir, apresentarei os códigos dos dois programas discutidos acima, mas, para começar, darei mais algumas explicações sobre o que e como.
Tirei todas as operações aritméticas de vetores em procedimentos separados (add, sub, mul, div) para aumentar a legibilidade do código. Todas as matrizes de entrada são inicializadas de acordo com as fórmulas que eu indiquei
quase aleatoriamente. Como o processo zero coleta os resultados do trabalho de todos os outros processos, portanto, funciona por mais tempo, portanto, é lógico considerar o tempo de seu trabalho igual ao tempo de execução do programa (como lembramos, estamos interessados em: aritmética + mensagens) no primeiro e no segundo casos.
Mediremos os intervalos de tempo usando a função
MPI_Wtime e, ao mesmo tempo, decidi exibir qual resolução dos relógios que tenho lá usando
MPI_Wtick (em algum lugar da minha alma espero que eles se encaixem no meu TSC invariante, neste caso, até estou pronto para perdoá-los pelo erro associado ao horário em que a função foi chamada MPI_Wtime). Então, reuniremos tudo o que escrevi acima e, de acordo com o gráfico, finalmente desenvolveremos esses programas (e depuraremos, é claro também).
Quem se importa em ver o código:
Programa com bloqueio de transferências de dados#include "pch.h" #include <iostream> #include <iomanip> #include <fstream> #include <mpi.h> using namespace std; void add(double *A, double *B, double *C, int n); void sub(double *A, double *B, double *C, int n); void mul(double *A, double *B, double *C, int n); void div(double *A, double *B, double *C, int n); int main(int argc, char **argv) { if (argc < 2) { return 1; } int n = atoi(argv[1]); int rank; double start_time, end_time; MPI_Status status; double *A = new double[n]; double *B = new double[n]; double *C = new double[n]; double *D = new double[n]; double *E = new double[n]; double *G = new double[n]; double *T0 = new double[n]; double *T1 = new double[n]; double *T2 = new double[n]; for (int i = 0; i < n; i++) { A[i] = double (2 * i + 1); B[i] = double(2 * i); C[i] = double(0.003 * (i + 1)); D[i] = A[i] * 0.001; E[i] = B[i]; G[i] = C[i]; } cout.setf(ios::fixed); cout << fixed << setprecision(9); MPI_Init(&argc, &argv); MPI_Comm_rank(MPI_COMM_WORLD, &rank); if (rank == 0) { start_time = MPI_Wtime(); sub(A, B, T0, n); MPI_Send(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD); MPI_Send(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD); div(T0, G, T1, n); MPI_Recv(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &status); add(T1, T2, T0, n); mul(T0, T1, T2, n); MPI_Recv(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &status); MPI_Send(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD); add(T0, T2, T1, n); MPI_Recv(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &status); MPI_Recv(T2, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &status); end_time = MPI_Wtime(); cout << "Clock resolution: " << MPI_Wtick() << " secs" << endl; cout << "Thread " << rank << " execution time: " << end_time - start_time << endl; } if (rank == 1) { add(C, C, T0, n); MPI_Recv(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &status); MPI_Send(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD); mul(T1, G, T2, n); add(T2, C, T0, n); MPI_Recv(T1, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &status); MPI_Send(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD); sub(T1, T0, T2, n); MPI_Recv(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &status); add(T0, T2, T1, n); MPI_Send(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD); } if (rank == 2) { mul(C, C, T0, n); MPI_Recv(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &status); MPI_Recv(T2, n, MPI_DOUBLE, 3, 0, MPI_COMM_WORLD, &status); MPI_Send(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD); MPI_Send(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD); add(T1, T2, T0, n); mul(T0, G, T1, n); MPI_Recv(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &status); mul(T1, T2, T0, n); MPI_Recv(T1, n, MPI_DOUBLE, 3, 0, MPI_COMM_WORLD, &status); mul(T0, T1, T2, n); MPI_Send(T2, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD); } if (rank == 3) { mul(E, D, T0, n); MPI_Send(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD); sub(T0, B, T1, n); mul(T1, T1, T2, n); sub(T1, G, T0, n); mul(T0, T2, T1, n); MPI_Send(T1, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD); } MPI_Finalize(); delete[] A; delete[] B; delete[] C; delete[] D; delete[] E; delete[] G; delete[] T0; delete[] T1; delete[] T2; return 0; } void add(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] + B[i]; } } void sub(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] - B[i]; } } void mul(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] * B[i]; } } void div(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] / B[i]; } }
Programa com transferências de dados não bloqueadas adiadas #include "pch.h" #include <iostream> #include <iomanip> #include <fstream> #include <mpi.h> using namespace std; void add(double *A, double *B, double *C, int n); void sub(double *A, double *B, double *C, int n); void mul(double *A, double *B, double *C, int n); void div(double *A, double *B, double *C, int n); int main(int argc, char **argv) { if (argc < 2) { return 1; } int n = atoi(argv[1]); int rank; double start_time, end_time; MPI_Request request[7]; MPI_Status statuses[4]; double *A = new double[n]; double *B = new double[n]; double *C = new double[n]; double *D = new double[n]; double *E = new double[n]; double *G = new double[n]; double *T0 = new double[n]; double *T1 = new double[n]; double *T2 = new double[n]; for (int i = 0; i < n; i++) { A[i] = double(2 * i + 1); B[i] = double(2 * i); C[i] = double(0.003 * (i + 1)); D[i] = A[i] * 0.001; E[i] = B[i]; G[i] = C[i]; } cout.setf(ios::fixed); cout << fixed << setprecision(9); MPI_Init(&argc, &argv); MPI_Comm_rank(MPI_COMM_WORLD, &rank); if (rank == 0) { start_time = MPI_Wtime(); MPI_Send_init(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[0]);// MPI_Send_init(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[1]);// MPI_Recv_init(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[2]);// MPI_Recv_init(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[3]);// MPI_Send_init(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[4]);// MPI_Recv_init(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[5]);// MPI_Recv_init(T2, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[6]);// MPI_Start(&request[2]); sub(A, B, T0, n); MPI_Startall(2, &request[0]); div(T0, G, T1, n); MPI_Waitall(3, &request[0], statuses); add(T1, T2, T0, n); mul(T0, T1, T2, n); MPI_Startall(2, &request[3]); MPI_Wait(&request[3], &statuses[0]); add(T0, T2, T1, n); MPI_Startall(2, &request[5]); MPI_Wait(&request[4], &statuses[0]); MPI_Waitall(2, &request[5], statuses); end_time = MPI_Wtime(); cout << "Clock resolution: " << MPI_Wtick() << " secs" << endl; cout << "Thread " << rank << " execution time: " << end_time - start_time << endl; } if (rank == 1) { MPI_Recv_init(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[0]);// MPI_Send_init(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[1]);// MPI_Recv_init(T1, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[2]);// MPI_Send_init(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[3]);// MPI_Recv_init(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[4]);// MPI_Send_init(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[5]);// MPI_Start(&request[0]); add(C, C, T0, n); MPI_Start(&request[1]); MPI_Wait(&request[0], &statuses[0]); mul(T1, G, T2, n); MPI_Start(&request[2]); MPI_Wait(&request[1], &statuses[0]); add(T2, C, T0, n); MPI_Start(&request[3]); MPI_Wait(&request[2], &statuses[0]); sub(T1, T0, T2, n); MPI_Wait(&request[3], &statuses[0]); MPI_Start(&request[4]); MPI_Wait(&request[4], &statuses[0]); add(T0, T2, T1, n); MPI_Start(&request[5]); MPI_Wait(&request[5], &statuses[0]); } if (rank == 2) { MPI_Recv_init(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[0]);// MPI_Recv_init(T2, n, MPI_DOUBLE, 3, 0, MPI_COMM_WORLD, &request[1]);// MPI_Send_init(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[2]);// MPI_Send_init(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[3]);// MPI_Recv_init(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[4]);// MPI_Recv_init(T1, n, MPI_DOUBLE, 3, 0, MPI_COMM_WORLD, &request[5]);// MPI_Send_init(T2, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[6]);// MPI_Startall(2, &request[0]); mul(C, C, T0, n); MPI_Startall(2, &request[2]); MPI_Waitall(4, &request[0], statuses); add(T1, T2, T0, n); MPI_Start(&request[4]); mul(T0, G, T1, n); MPI_Wait(&request[4], &statuses[0]); mul(T1, T2, T0, n); MPI_Start(&request[5]); MPI_Wait(&request[5], &statuses[0]); mul(T0, T1, T2, n); MPI_Start(&request[6]); MPI_Wait(&request[6], &statuses[0]); } if (rank == 3) { MPI_Send_init(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[0]); MPI_Send_init(T1, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[1]); mul(E, D, T0, n); MPI_Start(&request[0]); sub(T0, B, T1, n); mul(T1, T1, T2, n); MPI_Wait(&request[0], &statuses[0]); sub(T1, G, T0, n); mul(T0, T2, T1, n); MPI_Start(&request[1]); MPI_Wait(&request[1], &statuses[0]); } MPI_Finalize(); delete[] A; delete[] B; delete[] C; delete[] D; delete[] E; delete[] G; delete[] T0; delete[] T1; delete[] T2; return 0; } void add(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] + B[i]; } } void sub(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] - B[i]; } } void mul(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] * B[i]; } } void div(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] / B[i]; } }
Teste e análise
Vamos executar nossos programas para matrizes de tamanhos diferentes e ver o que acontece. Os resultados do teste estão resumidos na tabela, na última coluna da qual calculamos e escrevemos o coeficiente de aceleração, que definimos da seguinte forma: K
accele = T
ex. sem bloqueio. Bloco / T.
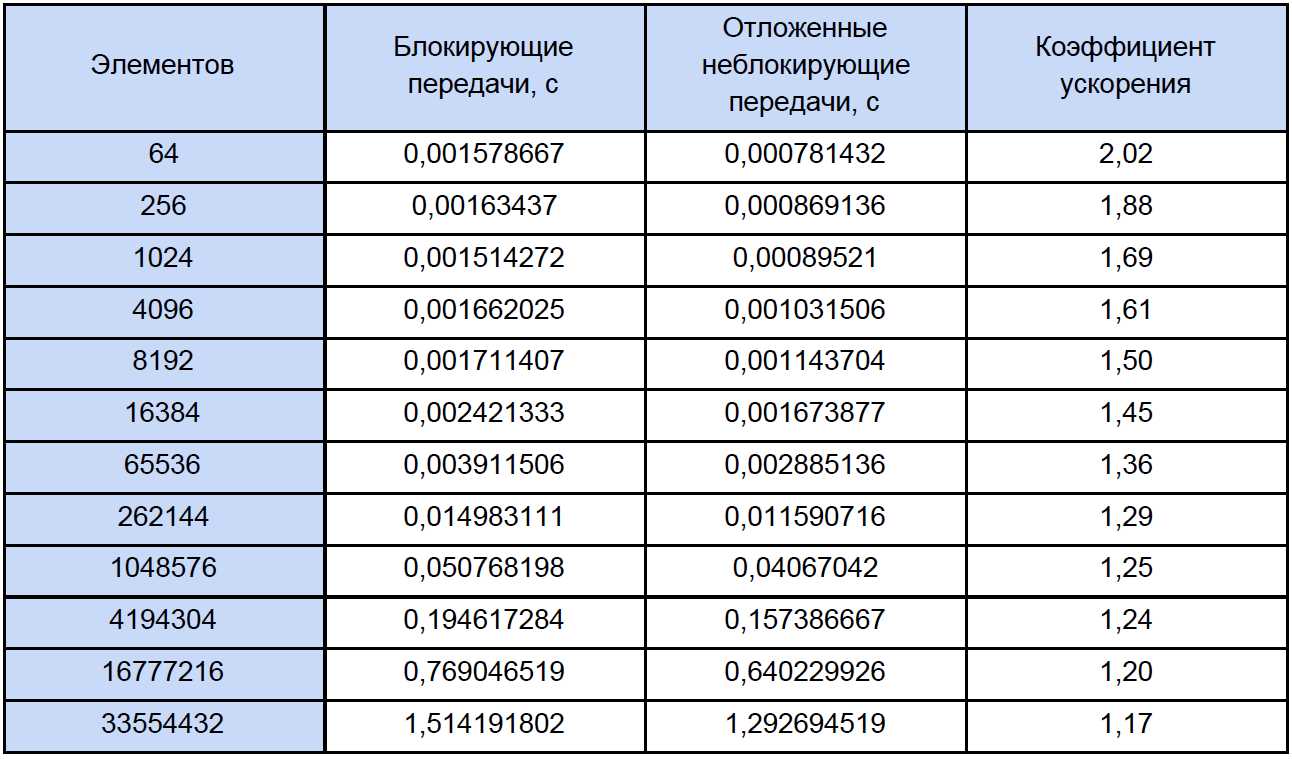
Se você observar esta tabela com um pouco mais de cuidado do que o habitual, notará que, com um aumento no número de elementos processados, o coeficiente de aceleração diminui de alguma forma da seguinte maneira:

Vamos tentar determinar qual é o problema? Para fazer isso, proponho escrever um pequeno programa de teste que medirá o tempo de cada operação aritmética de vetor e reduzirá cuidadosamente os resultados para um arquivo de texto comum.
Aqui, de fato, o próprio programa:
Medição do tempo #include "pch.h" #include <iostream> #include <iomanip> #include <Windows.h> #include <fstream> using namespace std; void add(double *A, double *B, double *C, int n); void sub(double *A, double *B, double *C, int n); void mul(double *A, double *B, double *C, int n); void div(double *A, double *B, double *C, int n); int main() { struct res { double add; double sub; double mul; double div; }; int i, j, k, n, loop; LARGE_INTEGER start_time, end_time, freq; ofstream fout("test_measuring.txt"); int N[12] = { 64, 256, 1024, 4096, 8192, 16384, 65536, 262144, 1048576, 4194304, 16777216, 33554432 }; SetConsoleOutputCP(1251); cout << " loop: "; cin >> loop; fout << setiosflags(ios::fixed) << setiosflags(ios::right) << setprecision(9); fout << " : " << loop << endl; fout << setw(10) << "\n " << setw(30) << ". (c)" << setw(30) << ". (c)" << setw(30) << ". (c)" << setw(30) << ". (c)" << endl; QueryPerformanceFrequency(&freq); cout << "\n : " << freq.QuadPart << " " << endl; for (k = 0; k < sizeof(N) / sizeof(int); k++) { res output = {}; n = N[k]; double *A = new double[n]; double *B = new double[n]; double *C = new double[n]; for (i = 0; i < n; i++) { A[i] = 2.0 * i; B[i] = 2.0 * i + 1; C[i] = 0; } for (j = 0; j < loop; j++) { QueryPerformanceCounter(&start_time); add(A, B, C, n); QueryPerformanceCounter(&end_time); output.add += double(end_time.QuadPart - start_time.QuadPart) / double(freq.QuadPart); QueryPerformanceCounter(&start_time); sub(A, B, C, n); QueryPerformanceCounter(&end_time); output.sub += double(end_time.QuadPart - start_time.QuadPart) / double(freq.QuadPart); QueryPerformanceCounter(&start_time); mul(A, B, C, n); QueryPerformanceCounter(&end_time); output.mul += double(end_time.QuadPart - start_time.QuadPart) / double(freq.QuadPart); QueryPerformanceCounter(&start_time); div(A, B, C, n); QueryPerformanceCounter(&end_time); output.div += double(end_time.QuadPart - start_time.QuadPart) / double(freq.QuadPart); } fout << setw(10) << n << setw(30) << output.add / loop << setw(30) << output.sub / loop << setw(30) << output.mul / loop << setw(30) << output.div / loop << endl; delete[] A; delete[] B; delete[] C; } fout.close(); cout << endl; system("pause"); return 0; } void add(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] + B[i]; } } void sub(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] - B[i]; } } void mul(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] * B[i]; } } void div(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] / B[i]; } }
Na inicialização, ele solicita que você insira o número de ciclos de medição, testei por 10.000 ciclos. Na saída, obtemos o resultado médio para cada operação:
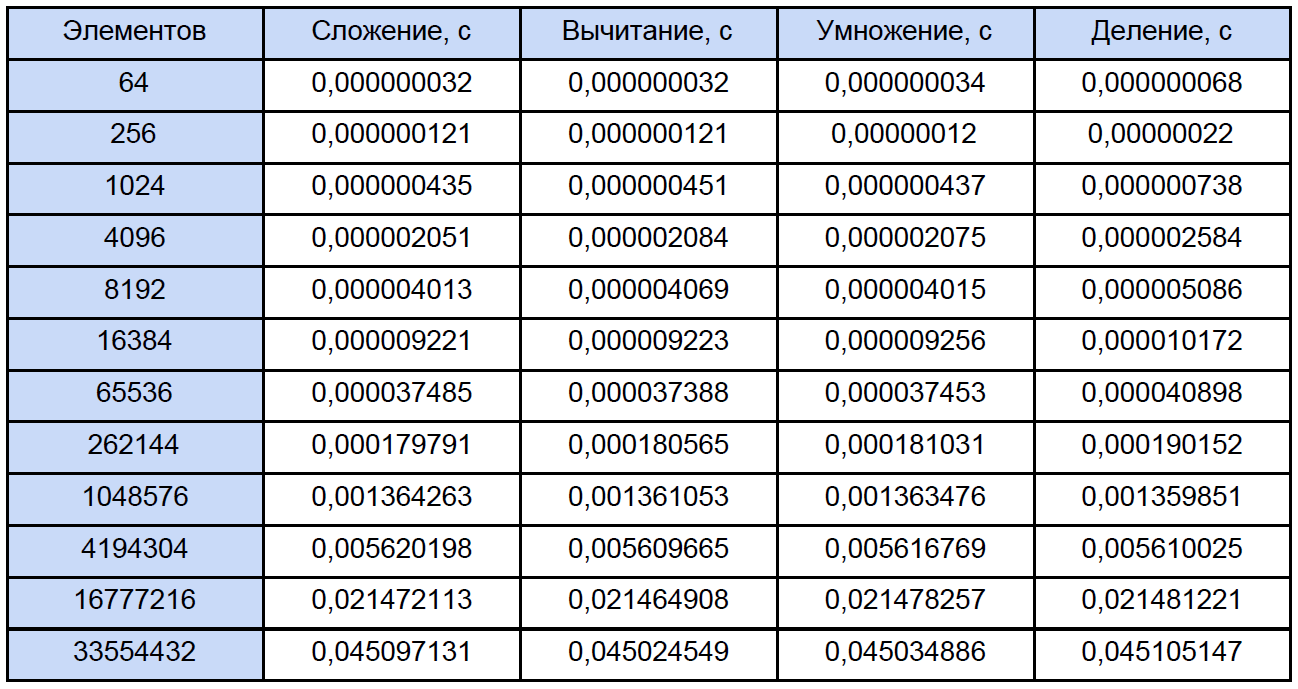
Para medir o tempo, usei o
QueryPerformanceCounter de alto nível. Eu recomendo fortemente a leitura
desta FAQ, para que a maioria das perguntas sobre a medição do tempo com esta função desapareça por conta própria. De acordo com minhas observações, ele se apega ao TSC (mas teoricamente pode não ser o caso), mas retorna, de acordo com a ajuda, o número atual de ticks do contador. Mas o fato é que meu contador fisicamente não pode medir o intervalo de tempo de 32 ns (consulte a primeira linha da tabela de resultados). Esse resultado se deve ao fato de que entre as duas chamadas dos ticks QueryPerformanceCounter 0. ou 1. Os ticks passam 1. Para a primeira linha da tabela, podemos concluir apenas que aproximadamente um terço dos 10.000 resultados são iguais a 1 tick.
Portanto, os dados nesta tabela para 64, 256 e até 1024 elementos são algo bastante aproximados. Agora, vamos abrir qualquer um dos programas e calcular quantas operações totais de cada tipo encontramos, tradicionalmente "espalharemos" tudo de acordo com a próxima tabela:
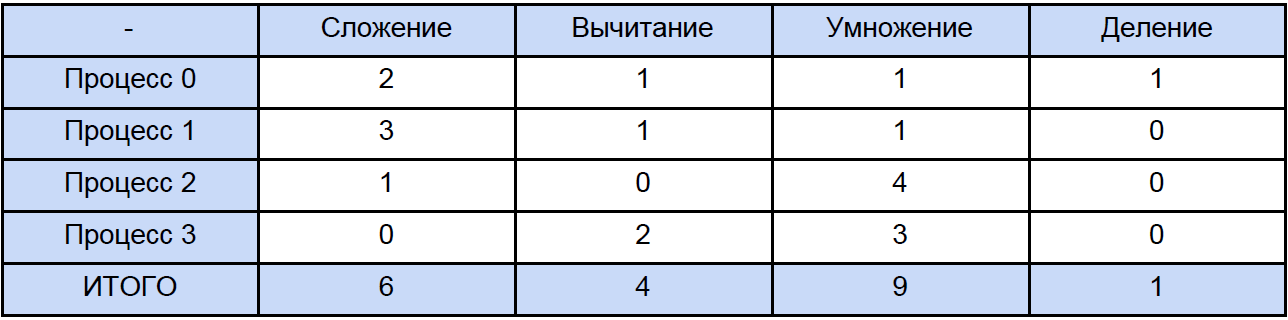
Por fim, sabemos o tempo de cada operação aritmética vetorial e quanto está em nosso programa, tentamos descobrir quanto tempo é gasto nessas operações em programas paralelos e quanto tempo é gasto no bloqueio e na troca de dados não-bloqueados adiados entre processos e, novamente, por questão de clareza, reduziremos isso para tabela:
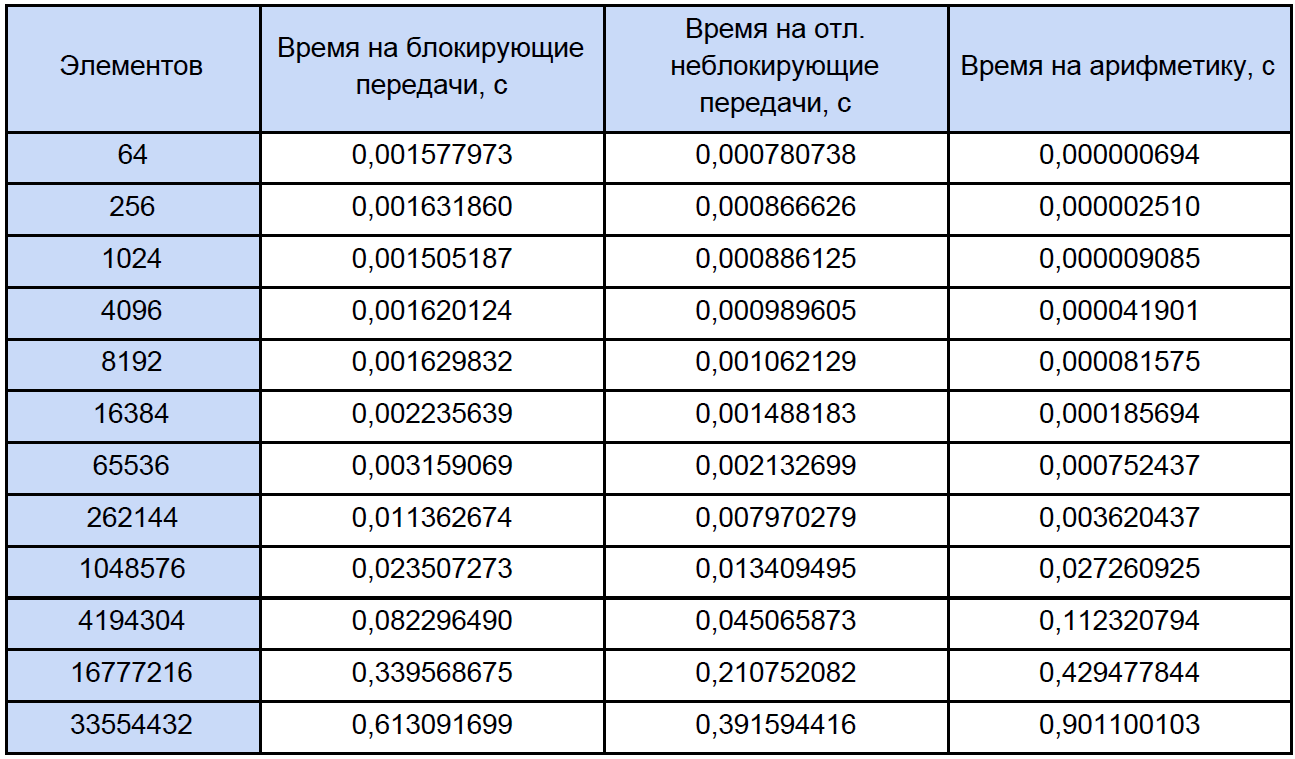
Com base nos resultados dos dados obtidos, construímos um gráfico de três funções: a primeira descreve a mudança no tempo gasto no bloqueio de transferências entre processos, a partir do número de elementos da matriz, a segunda descreve a mudança no tempo gasto em transferências não bloqueadas adiadas entre processos, no número de elementos da matriz e a terceira descreve a alteração no tempo, gastos em operações aritméticas, a partir do número de elementos de matrizes:
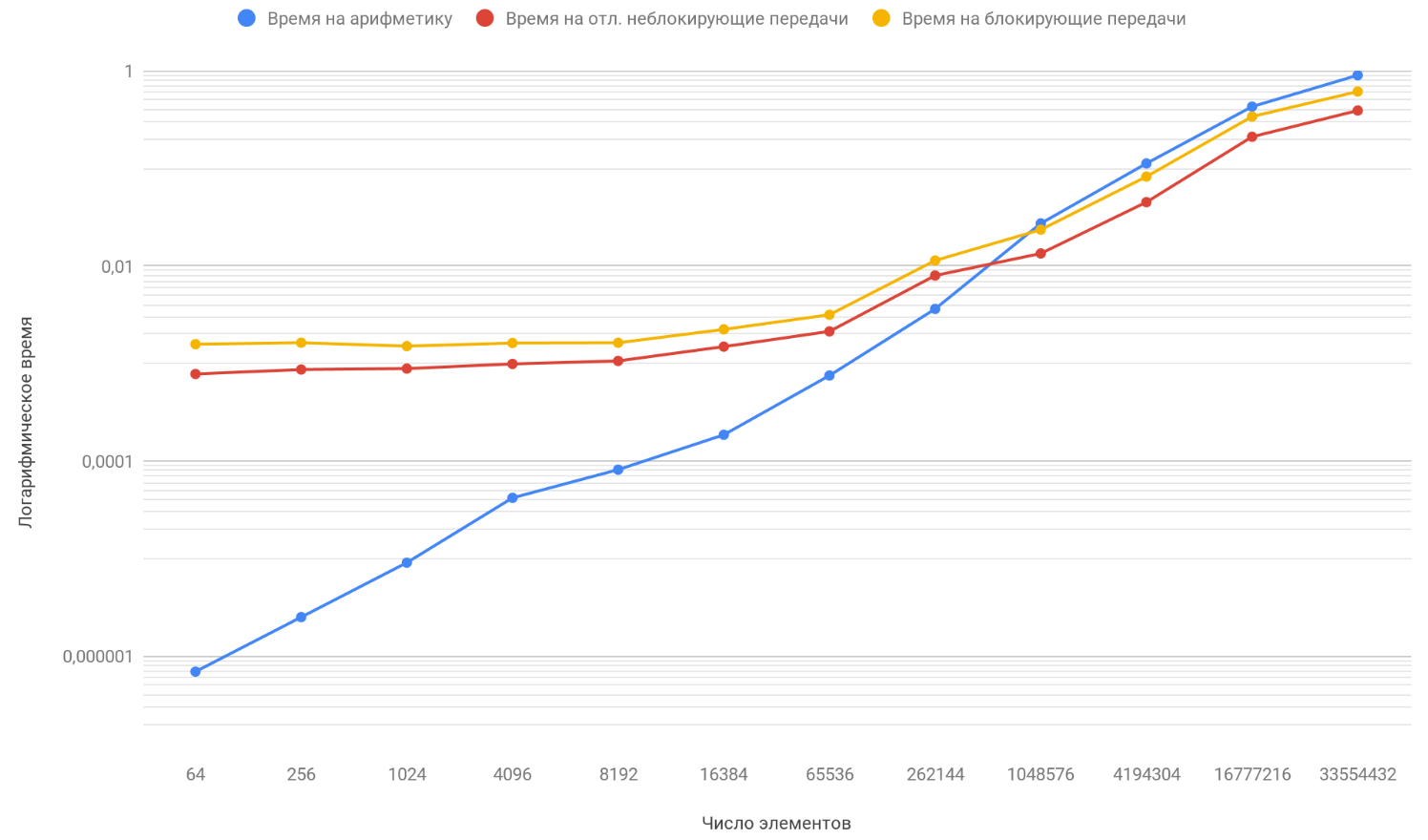
Como você já notou, a escala vertical do gráfico é logarítmica, é uma medida necessária, porque a dispersão dos tempos é muito grande e em um gráfico regular nada teria sido visível. Preste atenção à função da dependência do tempo gasto em aritmética no número de elementos, ele ultrapassa com segurança as outras duas funções em cerca de 1 milhão de elementos. O fato é que ele cresce no infinito mais rápido que seus dois oponentes. Portanto, com um aumento no número de elementos processados, o tempo de execução dos programas é cada vez mais determinado pela aritmética, e não pelas transferências. Suponha que você tenha aumentado o número de transferências entre processos; conceitualmente, você verá apenas que o momento em que a função aritmética ultrapassa as outras duas acontecerá mais tarde.
Sumário
Assim, continuando a aumentar o comprimento das matrizes, você chegará à conclusão de que um programa com transferências não bloqueadas adiadas será apenas um pouco mais rápido do que o que usa a troca de bloqueio. E se você direcionar o comprimento das matrizes para o infinito (bem, ou apenas realizar matrizes muito longas), o tempo de operação do seu programa será 100% determinado por cálculos, e o coeficiente de aceleração tenderá a 1.