Em março de 2016, Robert J. Lemke-Oliver e Kannan Sundararajan, da Universidade de Stanford,
abriram um novo padrão na distribuição de primos. Acontece que os números primos são distribuídos
especificamente pelo espaço numérico. Para mais detalhes, consulte a tradução do artigo
"Estrutura e aleatoriedade dos números primos" em Habré.
Especialistas de outras áreas, incluindo química, se juntaram ao estudo do tópico. E com sucesso. O professor de química teórica
Salvatore Torcuato, juntamente com o teórico dos números
Matthew de Courcy-Irlanda, encontrou
novos padrões na distribuição de primos que não eram conhecidos anteriormente. Descobriu-se que a distribuição de números primos forma um padrão de difração semelhante a fractal, algo semelhante ao padrão de difração de quasicristais exóticos.
O professor Torcuato é especialista no estudo de padrões nas estruturas dos sistemas físicos, como cristais e colóides. A maneira padrão de estudar a estrutura é a difração de raios-x. Moléculas aleatórias em líquidos ou gases refletem raios em todas as direções sem criar um padrão perceptível. Porém, átomos simetricamente localizados no cristal refletem sincronicamente as ondas de luz, criando pontos brilhantes periódicos de difração pronunciada (
picos de Bragg ). Uma análise dos picos de Bragg torna possível entender a estrutura interna de um cristal ou outro material que cria essa imagem.
Assim, em novos artigos científicos de Torkuato e outros (
1 ,
2 ,
3 ), é mostrado que a estrutura ordenada descoberta na distribuição de primos nada mais é do que um padrão de difração semelhante a fractal, semelhante ao dos quasicristais.
A imagem dos picos de Bragg em uma treliça de números primos é semelhante aos quase-cristais, mas ainda difere deles. Torcuato
diz que os primos como um sistema físico "são uma categoria completamente nova de estruturas". Os pesquisadores chamam esse novo padrão de fractal de "periodicidade limite efetiva".
A figura consiste em uma sequência periódica de picos brilhantes que refletem os intervalos primos mais comuns: todos são ímpares (exceto 2), muitos próximos um do outro. Os picos mais brilhantes (pares separados por dois dígitos) alternam-se a intervalos regulares com picos menos brilhantes, refletindo números primos separados por seis dígitos. Entre eles, há picos ainda mais fracos, correspondentes a pares de primos mais distantes, etc. Tudo isso é um número infinito de picos de Bragg, colocados um dentro do outro.
Uma estrutura semelhante dos picos de Bragg foi observada anteriormente - nos padrões de difração dos quasicristais.
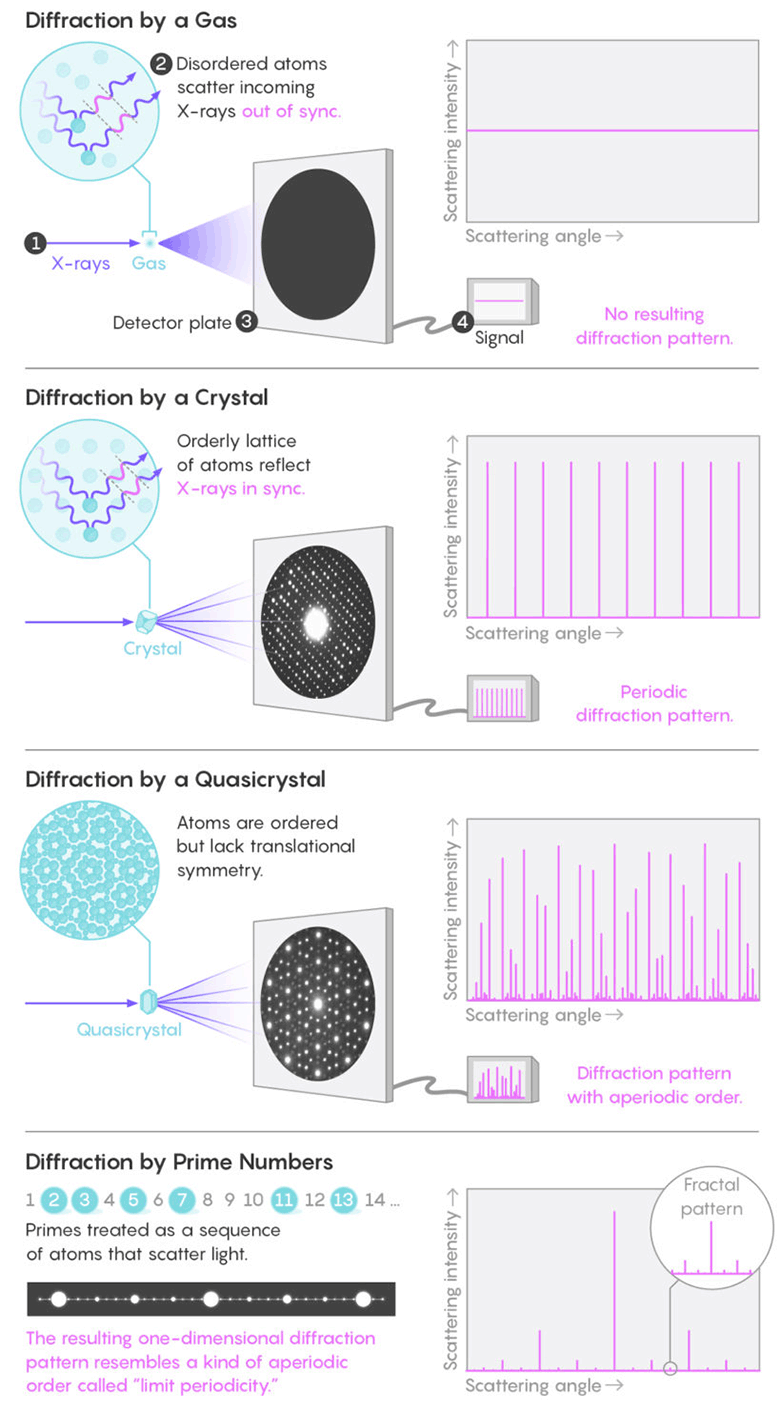Moléculas aleatórias em líquidos ou gases refletem raios em todas as direções sem criar um padrão perceptível. Porém, átomos simetricamente localizados em um cristal refletem sincronicamente as ondas de luz, criando pontos brilhantes periódicos de difração pronunciada. Como se viu, o padrão de distribuição dos primos forma um padrão de difração fractal, semelhante ao dos quase-cristaisOs quase-cristais são materiais estranhos descobertos na década de 1980. Eles são caracterizados pela simetria proibida na cristalografia clássica e pela presença de ordem de longo alcance. Mosaicos aperiódicos do tipo do famoso
mosaico de Penrose são um modelo matemático de quase-cristais. Nesses mosaicos, a simetria translacional está ausente, a repetibilidade e a quase cristalinidade estão presentes (simetria de quinta ordem).
Fragmento do mosaico de Penrose tipo P1 (de ladrilhos de seis tipos)No caso de números primos, as distâncias entre os picos são proporcionais entre si, em contraste com os picos de Bragg, espaçados irracionalmente, de quasicristais. "Os números primos na verdade implicam um estado completamente diferente das posições das partículas, semelhante aos quasicristais, mas não aos quasicristais",
disse Torcuato.
A descoberta do padrão de difração não pode ser chamada de descoberta inovadora para a teoria dos números, porque a parte principal desses padrões já foi descrita anteriormente, apenas por outros métodos matemáticos (não por difração de quasicristais). Portanto, usando o padrão de difração, é possível prever "duplas" dos tipos 17 e 19 - este é o equivalente matemático da
primeira hipótese de Hardy - Littlewood em relação à existência de tuplas de primos em um determinado segmento da linha numérica. Uma das regras proíbe trigêmeos de números ímpares consecutivos após {3, 5, 7}. Isso também explica por que o próximo pico de Bragg mais brilhante no padrão de difração corresponde a números separados por seis dígitos em vez de quatro.
Um novo trabalho científico é apenas uma nova visão do problema da distribuição uniforme de números primos e uma maneira mais fácil de derivar uma certa "lei única" para eles. Além disso, essa é uma maneira incomum de analisar um problema matemático do ponto de vista da cristalografia, ou seja, do ponto de vista de um campo de pesquisa relativamente jovem chamado de "ordem aperiódica", que estuda modelos não repetitivos e fica na interseção da cristalografia, sistemas dinâmicos, análise harmônica e geometria discreta. Esse ramo da ciência cresceu após a descoberta de quase-cristais, quando ficou claro que os métodos antigos não funcionavam aqui.
A distribuição dos primos se assemelha a uma ordem aperiódica especial, conhecida desde a década de 1950. É chamado periodicidade limite. Nesses sistemas, os intervalos periódicos são aninhados em uma hierarquia infinita, de modo que, em qualquer intervalo, o sistema contenha partes de padrões que são repetidas apenas em um intervalo maior, como no bloco Taylor-Sokolar.
Telha de Taylor-SokolarOs cálculos teóricos mostram que as fases periódicas máximas de uma substância devem ser capazes de se formar na natureza, e esses sistemas podem ter propriedades incomuns. Mas ninguém imaginou conectar a periodicidade limitante com números primos. Agora sabemos que existe essa conexão, e os números primos demonstram um novo tipo de periodicidade limite - periodicidade limite "efetiva", porque o sincronismo nas distâncias entre os primos no sistema é observado apenas estatisticamente.
Surge a pergunta: como os padrões na distribuição de números primos afetam a força dos algoritmos criptográficos?
“Recebo muitas cartas sobre esse assunto. Embora este seja um estudo interessante, não tem nada a ver com criptografia ”,
escreveu o famoso criptógrafo Bruce Schneier em seu blog. - Os criptografadores não estão interessados em encontrar números primos ou mesmo sua distribuição. A força dos algoritmos de criptografia de chave pública do tipo RSA está associada à complexidade de fatorar grandes números compostos, que são o produto de números primos. E este é um assunto completamente diferente. ”
Portanto, apesar do progresso no estudo da distribuição de números primos, ainda não há necessidade de se preocupar com a força dos códigos criptográficos.
