Problemas da escrita moderna de textos matemáticos

Em um artigo recente, o camarada KvanTTT levantou a questão :

Você pode explicar o que não gosta nas fórmulas modernas (declarações matemáticas e) e como pode ser melhorado?

Tentei responder em um comentário, mas o tamanho do campo de texto não me permitiu concluir os cálculos. Este artigo é uma resposta excessivamente detalhada.

Devo dizer que o material é holivarny. Em parte muito emocional. Muito controverso. Muito pessoal - geralmente baseado em experiência pessoal, não rico, embora diverso. O post se refere a livros escolares e universitários: a literatura “profissional” tem suas próprias especificidades, seu próprio público . Não há solução para o problema nas realidades atuais. Ao mesmo tempo, algumas de minhas observações muito antes de mim foram expressas por autoridades como Knut e Hamming; caras um pouco menos populares chegaram a ler a instrução " Como ler matemática ".

Portanto, na minha opinião, a principal reclamação não é tanto escrever fórmulas, como apresentar o material . Além disso, para a apresentação de material em quase todos os níveis de ensino, começando na escola e terminando com a ciência avançada. O início da situação atual foi marcado por Euclides, que declarou a ausência do caminho real na matemática. A estrada real ainda não foi pavimentada. Euclides fez, e nós podemos.

O primeiro problema é que o significado não é mostrado . Outro presente de Euclides: "Dê um centavo ao interlocutor se ele estiver procurando por benefícios, não por matemática". Os autores começam a introduzir definições, provar teoremas e fazer outras contas sem explicar por que é necessário. Exemplo: um livro de análise matemática de Fichtenholtz . Leia o primeiro capítulo: “do curso escolar você conhece números racionais, mas as necessidades da matemática nos forçam a introduzir números reais ...” e começou. Quais são as necessidades, que tipo de matemática, por que o racional não é feliz - sim, o cachorro o conhece. "Obviamente."

Ou outro exemplo do mesmo tutorial. "O número constante a é chamado limite de opções $$ se para cada positivo $$ por menor que seja, existe um número N tal que todos os valores $$ para o qual o número n> N satisfaz a igualdade $$ . ”

A maioria dos estudantes não entende a definição acima, mas depois de seis meses se acostuma. Ainda mais estudantes, mesmo no final de seus estudos, não sabem por que precisavam do conceito de limite de sequência. Da mesma forma, para funções, integrais, séries ... Fichtenholtz descreve alguns objetos matemáticos, às vezes dá exemplos particulares - e isso é tudo. Bem, sim, agora entendo que os limites são necessários, por exemplo, para a descrição correta das somas superior / inferior ao introduzir integrais, mas antes das integrais mais dois semestres!

Ou um determinante definido como uma função multilinear inclinada e simétrica. Gente, você está falando sério? A única resposta adequada de um aluno do primeiro ano a essa definição de "e daí"? Qual é o benefício dessa definição? Eu não discuto, há um benefício, mas qualquer calouro pode estar ciente disso?

Solução falsa para o problema : histórico. Aparece em todos os tipos de conferências. "O problema foi colocado por Jacó, examinado por seu discípulo Abel, e pelo discípulo de Caim, e pelas cento e quinhentas encarnações de Vishnu." Qual é a essência do problema, por que foi resolvido pelo autor original, por que é tão importante matar horas do professor nele - é omitido.

O próximo problema - os autores não apresentam problemas reais

Em princípio, é semelhante ao anterior. Lembre-se do curso da teoria das probabilidades. Que tarefas prevalecem lá? "Há 25 bolas pretas e 10 brancas na cesta ..." Exemplos de cassinos, cartas, D&D, econômicos - não, não ouvidos. Usaremos os exemplos mais politicamente corretos, embora a teoria das probabilidades tenha surgido a partir da pesquisa de dados.

Sobre exemplos ao vivo recentemente escreveu Free_Mic_RS


A matemática começa com uma tarefa. E tarefas mortas e unilaterais deixam a impressão de que a teoria só funciona com elas. A intenção dos autores é boa: dar um exemplo e depois passar para o geral. Resumo do exemplo. Mas alguns exemplos "vivos" tornariam a transição para a abstração muito mais útil. Pelo menos, acredito firmemente que o processo inverso (a transição de abstrato para particular) seria muito mais fácil.

Problema: brevidade excessiva e inconsistência

Lembra da escola? E a fórmula discriminante? E como é provado / derivado? Uma maneira: puramente algébrica . Tomamos a equação $$ , "Multiplique cada parte por $$ e adicione $$ "( Por que exatamente esses valores? ), Mais algumas transformações - e pronto. Depois de discriminantes, os alunos recebem discriminantes por pares. E então as fórmulas Vieta. E também quadrados completos. E um monte de exemplos. E longe de sempre explicar por que todos esses métodos são necessários.

Agora imagine a situação, é dito ao aluno: “hoje vamos aprender a resolver equações com $$ . Qualquer. E uma série de exemplos começa com complicações.

$$

Muitos exemplos que conduzem organicamente à solução da equação através de quadrados completos. Depois, você pode inserir o discriminante (como um algoritmo simples para resolver equações quando os alunos se cansam de destacar os quadrados completos) e o Viet com um discriminante ainda mais "know-how".

Uma abordagem semelhante é usada nos livros didáticos. Infelizmente, não em todos. E nem em todos os lugares uma sequência clara é visível. Segundo rumores, alguns autores perderam rascunhos em bondes e depois substituíram as peças perdidas por expressões como "é fácil mostrar isso ...". Como resultado, em vez de pular com calma de exemplo em exemplo, os alunos foram forçados a pular o abismo. Quantas pessoas quebraram e ainda quebram por 10 + 6 anos de escolaridade / universidade?

Exemplo pessoal (solicitado na postagem original). No primeiro ano de matan, sofri. Silenciosamente resolvendo os exemplos, ele não aprendeu a teoria. Pedi ajuda a um colega de classe para calcular o comprimento da curva através da integral. Ele pegou uma garrafa de cerveja, desenhou uma curva aleatória, endireitou-a com segmentos infinitamente pequenos, selecionou um desses segmentos, construiu-o no triângulo dl, dx, dy e perguntou: “Você se lembra do teorema de Pitágoras”? Então tudo foi simples.



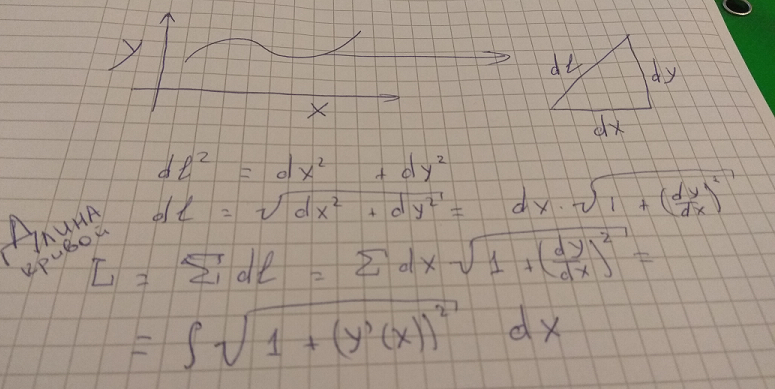
Perguntei-lhe: por que isso não é mostrado em pares / em livros didáticos? Ele mostrou alguns contra-exemplos, explicou por que o formalismo é necessário em matan - e eu fiquei atolado. Acabei de ler o teorema, destacar o principal, escrever / resolver exemplos triviais, depois lidar com o formalismo - e realmente entender o que estava acontecendo.

Não sei se é possível usar massivamente a abordagem geral da visão geral => contra-exemplos => formalismo . Não sei quanto e qual teoria / prática um aluno precisa obter antes do "avanço"; mal posso imaginar como colocar experimentos pedagógicos sobre esse tópico e quanto trabalho terei que investir em pesquisa. Mas a memória dessa explicação vive há 10 anos. E depois de todos esses anos, tento primeiro dar uma visão geral ao público, depois mostrar os problemas e depois mergulhar nos detalhes.

Você dirá que meus sentimentos pessoais podem estar errados. Além deles, tenho apenas idéias semelhantes de Hamming :

... Eu poderia estudar quais métodos eram eficazes e quais não eram. Ao participar de reuniões, já estudei por que alguns trabalhos são lembrados e a maioria não. Uma pessoa técnica deseja dar uma palestra técnica muito limitada. Como regra, o público quer uma palestra ampla de natureza geral e quer uma visão geral e apresentações muito mais gerais do que o orador deseja dar. Como resultado, muitas palestras são ineficazes. O palestrante chama o tópico e de repente mergulha nos detalhes. Poucas pessoas podem acompanhar. Você deve desenhar um quadro geral para explicar por que isso é importante e depois desdobrar lentamente um esboço do que foi feito. Mais pessoas dirão: “Sim, Joe fez” ou “Mary fez o que realmente vejo do que se trata. Sim, Mary deu uma palestra muito boa, eu entendo o que ela fez. " Como regra, as pessoas fazem uma palestra muito limitada e segura; geralmente é ineficaz. Além disso, muitas palestras são preenchidas com informações ...

Ideias em massa

Devo dizer que minha experiência no ensino é extremamente limitada. Você deve ter notado que eu me limitei ao currículo e matanaliz da escola. Infelizmente, são essas as áreas em que tive a oportunidade de colocar a teoria em contato com a prática. Ainda não entendo a essência do determinante na álgebra, não percebo a geometria projetiva e, apenas seis meses atrás, comecei a penetrar nas matrizes (logo após o treino, hein). Uma boa ilustração do ditado "teoria sem prática está morta".

Como me disseram, na NMU, um novo conceito sempre foi introduzido com uma dúzia de perguntas. E se sim? E se esta cláusula não for cumprida? O que é necessário para complementar nosso conceito em um semigrupo? Os ouvintes foram autorizados a brincar com o assunto. Acostume-se a isso. Eu acho que vale a pena pensar cuidadosamente sobre a experiência do NMU.

Certamente, nos ramos superiores da matemática, a abordagem “primeiro um exemplo, depois uma abstração” não funcionará. Portanto, exemplos em um pedaço de papel não ajudam a realizar a RSA. Mas o tempo de crescimento do programa com o aumento da duração das chaves ajuda a sentir os aspectos puramente práticos.

Há um medo de que os livros escolares “ideais / com efeito de estufa” levem a choque ao trabalhar com a “torre”. Parece que "um trabalhador hardcore precisa ser educado desde tenra idade".

É muito difícil desenvolver cursos, esperando que os alunos já saibam alguma coisa. Quanto maior a base necessária, maior a probabilidade de que algo da base seja mal interpretado pelo aluno.

Eles dizem que o pico da forma dos matemáticos é de 30 anos. Depois dos 30, você já pode carregá-los para escrever livros, dando a um parceiro um metodologista especialista.

A tecnologia atual permite escrever textos usando o git. Um artigo sobre a compilação do TeXa em pdf no processo de IC recentemente caiu em um hub Estou certo de que uma equipe de autores com boas ferramentas pode escrever livros muito melhores.

Além de professores, professores, alunos e alunos, há estados em matemática. E regulamentos. E os requisitos. E certificação. Tudo isso afeta os livros, autores, professores e a qualidade do material.

Como melhorar o fluxo de material em textos matemáticos

Nas realidades atuais (russas) - nada. Há entusiastas, profissionais, sem motivação.

Os professores de matemática têm tarefas suficientes para escrever livros didáticos. Às vezes, não há habilidades puramente humanitárias suficientes; os livros não são ensinados nas universidades. Além disso, deformação profissional: o "óbvio" para um professor pode ser esmagador para os alunos. Professores de matemática estão ocupados. E papéis. E aulas particulares. Não direi nada sobre o estado. Quase não encontrou seus representantes, então não há nada a dizer. A menos que eu mencione a política de substituir livros didáticos a cada três anos. Depois da escola, eu queria levar meus livros para a biblioteca, eles me disseram "são velhos, você não pode ficar com eles". A motivação para escrever bons livros didáticos não adiciona essa abordagem.

Em outras palavras, eu pessoalmente não espero progresso positivo do sistema educacional. Espero, é claro, mas não espero. O que ajuda são vislumbres de TI e outras engenharias. Em uma das conferências de matemática, recebi um livro sobre computação gráfica de um dos participantes. O autor trabalhou em um escritório desenvolvendo um núcleo gráfico de algum sistema de desenho, e o material era bastante bom. A matemática não era "pura", aplicada, mas o fato da existência de um bom material educacional era certamente agradável.

Outra abordagem: professores de empresas que trabalham em universidades. Textos matemáticos desses caras não podem ser esperados, os detalhes não são os mesmos. A menos que os desenvolvedores de jogos escrevam um manual sobre a teoria, ou os gráficos escreverão sobre a álgebra / geometria necessária para desenvolver os mesmos sistemas CAD (se houver projetos - chamada) .

Por fim, existem várias plataformas educacionais não estatais, como o mesmo Coursera. Esses caras podem fazer qualquer coisa, porque trabalham por dinheiro, competem e recebem feedback rapidamente. Mas eles têm sua própria desvantagem: o formato para enviar dados é diferente. Eles não escrevem textos diretamente.

E o que virá no futuro?

Mais interessante. Talvez tudo permaneça como está. Talvez haja um desvio dos textos em matemática. Ou talvez os autores se inspirem na idéia "o texto do produto deve ser conveniente para o cliente do leitor" e os pioneiros serão capazes de quebrar a tradição. Então, em 30-50-100 anos, teremos livros didáticos que são compreensíveis para a maioria dos leitores.

Upd1. Inseri uma foto com o cálculo do comprimento da seção da curva.

Upd2. Nos comentários, é freqüentemente mencionado que o texto é dedicado aos problemas do ensino, e não à matemática profissional. O motivo é simples: a maior parte do trabalho "profissional" que vi em termos de apresentação de material não difere dos livros didáticos. Ao mesmo tempo, a literatura da escola / universidade é conhecida pela maioria no habr e "profissional" por cento.