Robomobiles sem motoristas entregam pizza. Os táxis sem motoristas transportam pessoas. Caminhões sem motoristas transportam cargas de várias toneladas. Se analisarmos todos esses projetos espetaculares, chegaremos a diferentes tarefas típicas, a mais importante delas é a busca e otimização de rotas. Tais problemas são resolvidos usando a
teoria dos grafos . Este tópico não é simples, é estudado principalmente na universidade ou, pelo menos, nas classes especializadas sênior. Mas neste post, mostrarei como usar o LEGO EV3 para aprender teoria dos grafos já no ensino médio. E sem amontoar, mas em um nível aplicado fascinante.
 Transportador automotivo Danny's LAB EV3 Realmente coleta carros LEGO. Mas não é um pouco sobre ele.
Transportador automotivo Danny's LAB EV3 Realmente coleta carros LEGO. Mas não é um pouco sobre ele.Para que o transporte não tripulado chegue onde é necessário, ele deve ser capaz de construir uma rota entre os pontos determinados. O mais curto e consistente com as regras de tráfego é desejável. Para simular e resolver esse problema, precisamos da plataforma móvel LEGO EV3 e, de fato, o mapa no qual essa plataforma será movida.
Plataforma móvel LEGO EV3
Nossa plataforma móvel deve estar equipada com sensores e servos. Tudo o que você precisa pode ser encontrado no conjunto educacional básico do LEGO Mindstorms EV3 45544. Veja como é a plataforma:

A montagem não requer conhecimento de eletrônica e não leva mais que meia hora. A plataforma tem tudo o que você precisa para atingir um alto nível de abstração na solução de um problema.
Roteiro
Vamos desenhar um roteiro na forma de uma grade. Linhas são estradas, pontos de interseção são interseções de estradas:
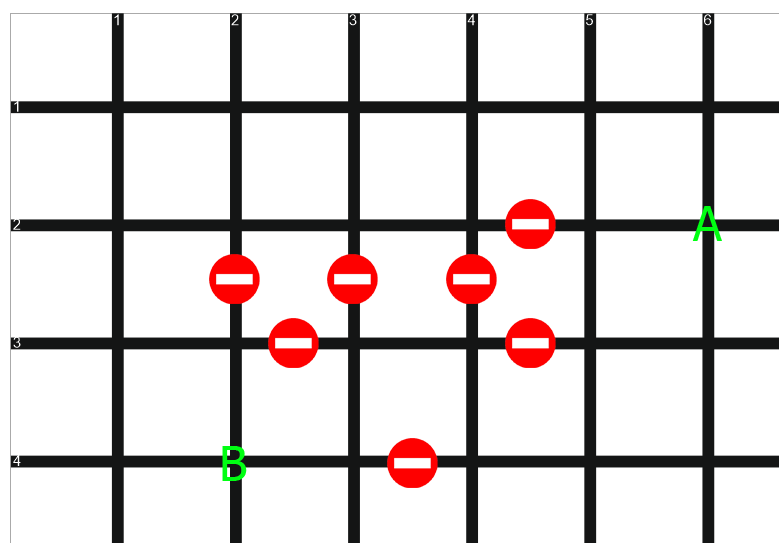
Todas as seções da estrada entre os cruzamentos têm o mesmo comprimento, o tráfego nelas é de mão dupla. Algumas estradas estão bloqueadas - elas são marcadas com um "tijolo". Além disso, todas as curvas no nosso mapa são múltiplos de 90 graus. A complicação da grade de estradas não afetará o princípio de resolver o problema e, para maior clareza, faremos com uma opção bastante simples. Nossa tarefa é dirigir do ponto A ao ponto B sobre o caminho mais curto.
Contagem
Cada interseção possui suas próprias coordenadas - os números das linhas horizontal e vertical. Na teoria dos grafos, essas interseções são chamadas
vértices . As estradas entre cruzamentos são indicadas por setas. Na teoria dos grafos, essas são
arestas . Todas as estradas são de mão dupla (setas nas duas direções) significa que o gráfico
não é
orientado . O custo (tempo de viagem) é o mesmo para todas as seções da estrada, o que significa que o gráfico
não está
ponderado .

Matriz de adjacência
O gráfico representado pela figura mostra claramente o mapa e as conexões dentro dele. Mas em um computador - incluindo o EV3 - é trabalhoso processar informações gráficas. É ideal codificar um gráfico com uma matriz, uma matriz de adjacência.
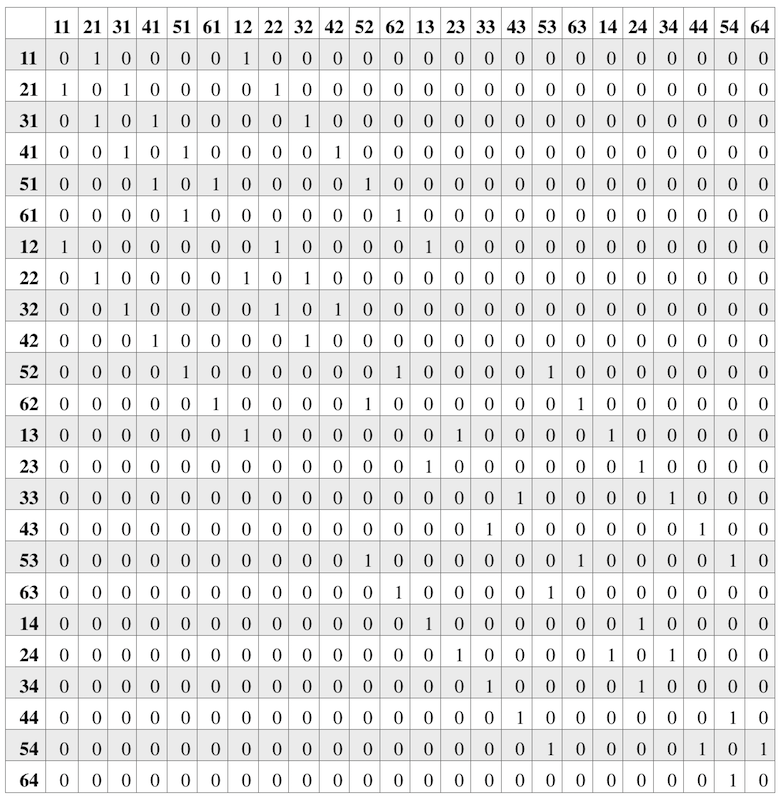
Se não houver conexão direta entre as interseções, colocaremos 0. Se houver - 1. Se houver - 1. Concordamos que todas as distâncias entre interseções adjacentes são iguais a 1. Se o gráfico for ponderado, em vez de uma em cada interseção, colocaremos “ peso ”da trama. E se a direção do movimento fosse levada em consideração, a matriz acima seria assimétrica - em uma direção poderia ser 1 e na outra 0.
Com uma matriz de adjacência, nosso robô já pode resolver o problema - encontre o caminho mais curto de A a B. Mas temos uma matriz bidimensional e, no EV3, apenas matrizes unidimensionais podem ser armazenadas. Podemos facilmente ir para uma matriz unidimensional através do deslocamento n * Y + X, onde n é o tamanho da matriz.
Algoritmo de Dijkstra
O algoritmo Dijkstra, o algoritmo para encontrar o caminho mais curto entre um vértice de um gráfico e todos os outros, será usado para resolver. O algoritmo foi inventado em 1956 pelo cientista holandês Edsger Dijkstroy. Se a explicação for o mais simples possível, o algoritmo será baseado no progresso seqüencial dos vértices vizinhos do gráfico, com uma avaliação constante da distância percorrida. Um bom exemplo ilustrativo e um fluxograma básico do algoritmo podem ser encontrados no artigo da Wikipedia.
No nosso caso, o fluxograma do algoritmo Dijkstra (nosso “Dijkstra”) ficará assim:
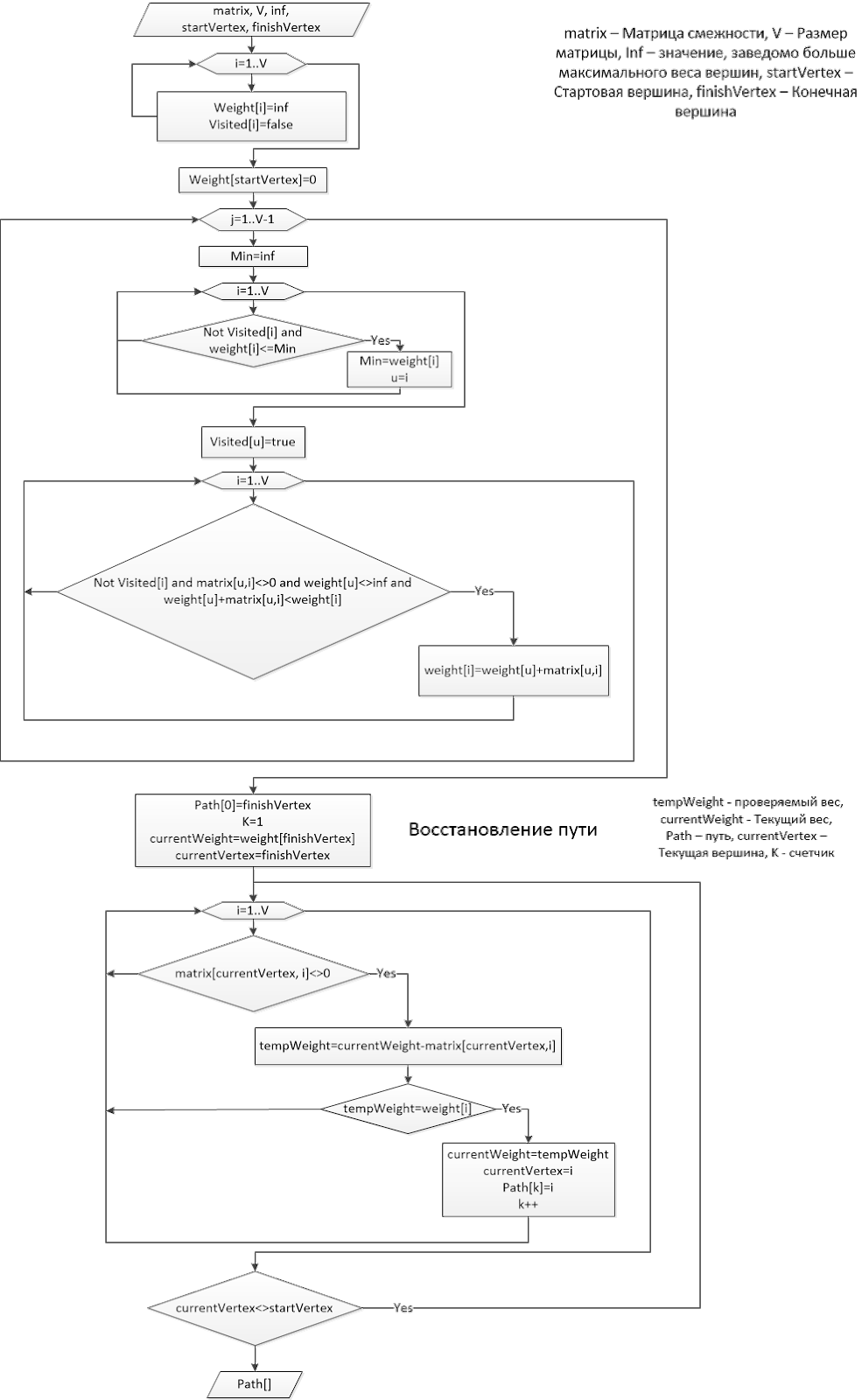
De acordo com o algoritmo, e melhor de acordo com seu modelo matemático, já podemos criar um programa para o robô. A entrada será a matriz de adjacência, os pontos inicial e final. Após todas as ações descritas, é possível encontrar rapidamente o caminho mais curto entre todos os pontos no mesmo mapa.
É claro que, além do algoritmo de Dijkstra, nosso robô baseado em LEGO EV3 precisará de vários módulos de programas (subprogramas) mais simples: movendo-se ao longo da linha até o cruzamento, contando cruzamentos, girando nas duas direções, determinando sua localização em relação ao sistema de coordenadas absolutas X, Y, where, onde X, Y - coordena na grade, Θ - a direção atual do robô (expressa através do código, por exemplo, 1 - para cima, 2 - para a direita, 3 - para baixo, 4 - para a esquerda).
E aqui está uma demonstração ao vivo da solução para o problema. Os dados de entrada são ligeiramente diferentes, mas isso não muda a essência.Tema bônus: odometria
Os recursos de odômetro podem ser integrados em tarefas de movimentação no solo - por exemplo, para que o robô no labirinto entenda onde está e para onde está se movendo. Usando a odometria, o movimento do robô é estimado com base em dados do movimento dos acionamentos (rotação dos motores). Conhecendo o diâmetro das rodas, podemos calcular a distância que o robô percorreu em um determinado período de tempo. Conhecendo a velocidade angular das rodas, podemos determinar o ângulo pelo qual o robô girou em relação ao original. E, definindo diferentes velocidades angulares, podemos ajustar o movimento do robô ao longo do arco e, ao mesmo tempo, determinar os "loops" ao mover o robô, como no vídeo abaixo:
Nas escolas, muita atenção é dada à trigonometria, mas sua aplicação prática não é abordada de forma alguma. Problemas de odometria resolvidos com o LEGO EV3 mostram por que a trigonometria pode ser necessária. Na prática, a odometria é usada não apenas no transporte, mas também, por exemplo, para rastrear a posição de uma ferramenta em máquinas CNC (controle numérico).
Onde posso aprender tudo isso?
Eu me permito alguma publicidade. A tarefa descrita acima e tarefas mais complexas podem muito bem ser resolvidas por crianças de 7 a 9 anos que foram treinadas em clubes de robótica. Dirijo um desses clubes, Robit, em Ecaterimburgo - este é o nosso
programa de treinamento . Filmamos o vídeo da demo para a tarefa acima em uma das classes. Então, um aluno da oitava série do nosso clube em 6 horas estudou os conceitos básicos da teoria dos grafos e resolveu um problema semelhante.
Como escolher um ambiente de programação LEGO EV3
A solução de problemas é impossível sem escolher o ambiente de programação certo para o LEGO EV3. Há
material separado sobre o mais recente nesta área. Tento ensinar as crianças a escolher uma linguagem de programação para a tarefa, e não uma tarefa para essa linguagem de programação, cuja sintaxe eles aprenderam. Porém, nas séries mais baixas, é difícil trabalhar imediatamente em uma linguagem de programação baseada em texto; portanto, começamos a estudar algoritmos em linguagens gráficas, onde o limiar de entrada é mais baixo. A partir dos 10 anos, os alunos aprendem o ambiente gráfico do EV3 Mindstorms. Algumas competições de robótica restringem os kits de ferramentas apenas a esse ambiente.
A partir dos 12 anos, os caras começam a dominar o ambiente básico do EV3. O ambiente é relativamente fácil de aprender e o Basic oferece uma funcionalidade poderosa para a plataforma LEGO EV3. Além disso, programamos no ambiente EV3Dev, onde você pode instalar muitas linguagens diferentes - Python, Java, C. Com o EV3Dev, os caras obtêm sua primeira experiência em linguagens populares e de tendências. O único ponto negativo do EV3Dev é uma taxa de pesquisa de sensor relativamente menor em comparação com outros ambientes. Com a abordagem correta, o LEGO EV3 se torna uma ótima ferramenta para conhecer a programação. Quando os alunos veem seu código dando vida a um construtor, essa é uma excelente motivação.
O que vem a seguir?
Depois de estudar esses algoritmos no ensino médio, as crianças serão capazes de consolidar ainda mais seus conhecimentos e, por exemplo, participar de olimpíadas de design e disciplinas que dão bônus reais - por exemplo, 100 pontos automaticamente no exame para admissão em universidades.