🤙 🧘🏽 👨🏾‍⚖️ Sobre a resolubilidade de problemas na via em tempo polinomial 🎀 🕋 👩🏽‍🎨

Os alunos conhecem o problema do caminho realizando cursos de bioinformática, em particular, um dos mais de alta qualidade e espírito mais próximo dos programadores - curso de bioinformática (Pavel Pevzner) sobre coursera da Universidade da Califórnia em San Diego. O problema chama a atenção pela simplicidade da declaração, pela importância prática e pelo fato de ainda ser considerado não resolvido com a aparente capacidade de resolvê-lo com codificação simples. O problema é colocado dessa maneira. É possível restaurar as coordenadas de um conjunto de pontos no tempo polinomial

$ inline $ X $ inline $ se o conjunto de todas as distâncias entre pares for conhecido

$ inline $ \ Delta X $ inline $ ?Essa tarefa aparentemente simples ainda está na lista de problemas não resolvidos da geometria computacional. Além disso, a situação nem sequer diz respeito a pontos em espaços multidimensionais, especialmente os curvos, o problema já é a opção mais simples - quando todos os pontos têm coordenadas inteiras e estão localizados na mesma linha.Nos últimos quase meio século desde que essa tarefa foi reconhecida pelos matemáticos como um desafio (Shamos, 1975), alguns resultados foram obtidos. Consideramos dois casos possíveis para um problema unidimensional:

pontos estão localizados em uma linha reta (problema na estrada)
pontos estão localizados em um círculo (problema da faixa)

Esses dois casos receberam nomes diferentes por um motivo - são necessários esforços diferentes para resolvê-los. De fato, a primeira tarefa foi resolvida com rapidez suficiente (em 15 anos) e um algoritmo de retorno foi construído, que restaura a solução em média em tempo quadrático

$ inline $ O (n ^ 2 \ log n) $ inline $ onde

$ inline $ n $ inline $ - o número de pontos (Skiena, 1990); para a segunda tarefa, isso ainda não foi feito e o melhor algoritmo proposto possui complexidade computacional exponencial

$ inline $ O (n ^ n \ log n) $ inline $ (Lemke, 2003). A imagem abaixo mostra uma estimativa de quanto tempo o seu computador funcionará para obter uma solução para um conjunto com um número diferente de pontos.

Ou seja, em um tempo psicologicamente aceitável (~ 10 s), você pode restaurar muitos

$ inline $ X $ inline $ até 10 mil pontos em uma caixa de pedágio e apenas ~ 10 pontos em uma caixa de cinto, o que é absolutamente inútil para aplicações práticas.Um pouco de esclarecimento. Acredita-se que o problema do turnpike seja resolvido em termos de uso prático, ou seja, para a grande maioria dos dados encontrados. Nesse caso, as objeções dos matemáticos puros ao fato de haver conjuntos de dados especiais para os quais o tempo para obter uma solução exponencialmente é ignorado

$ inline $ O (2 ^ n \ log n) $ inline $ (Zhang, 1982). Ao contrário do turnpike, o problema da via com seu algoritmo exponencial não pode ser considerado resolvido de forma alguma.

Importância da resolução de problemas de via em termos de bioinformática

No final do século 20, foi descoberta uma nova via para a síntese de biomoléculas, chamada via não-ribossômica de síntese. Sua principal diferença em relação à via clássica de síntese é que o resultado final da síntese não é codificado no DNA. Em vez disso, apenas o código de "ferramentas" (muitas sintetases diferentes) que podem coletar esses objetos é gravado no DNA. Assim, a engenharia de biomaquinas é significativamente enriquecida e, em vez de um único tipo de coletor (ribossomo), que trabalha com apenas 20 partes padrão (aminoácidos padrão, também chamados de proteinogênicos), muitos outros tipos de coletores aparecem que podem trabalhar com mais de 500 partes padrão e não padrão (aminoácidos não proteogênicos e suas várias modificações). E esses montadores podem não apenas conectar peças em cadeias, mas também obter estruturas muito complexas - cíclicas, ramificadas, bem como estruturas com muitos ciclos e ramificações. Tudo isso aumenta significativamente o arsenal da célula em vários casos de sua vida. A atividade biológica de tais estruturas é alta, a especificidade (seletividade da ação) e também uma variedade de propriedades não é limitada. A classe desses produtos celulares na literatura inglesa é denominada NRPs (produtos não ribossômicos ou peptídeos não ribossômicos). Os biólogos esperam que seja precisamente entre esses produtos do metabolismo celular que podem ser encontradas novas preparações farmacológicas que são altamente eficazes e não apresentam efeitos colaterais devido à especificidade.A única questão é: como e onde procurar NRPs? Eles são muito eficazes, portanto a célula não tem absolutamente nenhuma necessidade de produzi-los em grandes quantidades, e suas concentrações são insignificantes. Portanto, métodos de extração química com baixa precisão de ~ 1% e enormes custos com reagentes e tempo são inúteis. Próximo. Eles não são codificados no DNA, o que significa que todos os bancos de dados acumulados durante a decodificação do genoma e todos os métodos de bioinformática e genômica também são inúteis. A única maneira de encontrar algo é através de métodos físicos, a saber, espectroscopia de massa. Além disso, o nível de detecção de substâncias nos espectrômetros modernos é tão alto que permite encontrar quantidades insignificantes, no total> ~ 800 moléculas (faixa atto-molar ou concentração

$ inline $ 10 ^ {- 18} $ inline $ )

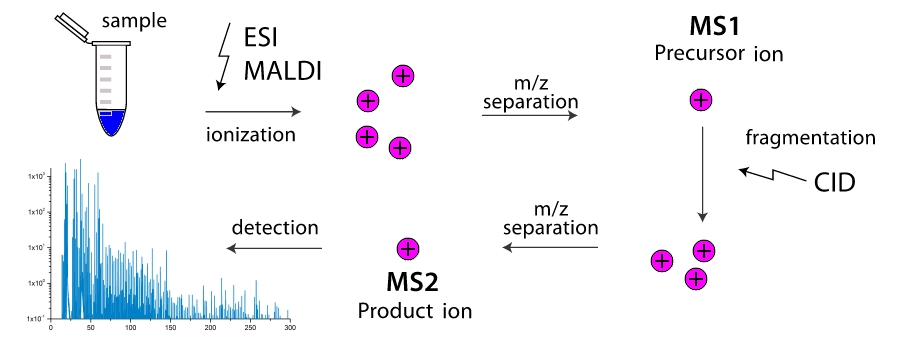
"Como um espectrômetro de massa funciona? Na câmara de trabalho do dispositivo, as moléculas são divididas em fragmentos (mais frequentemente através de colisões entre si, menos frequentemente devido a influências externas). Esses fragmentos são ionizados e depois acelerados e separados em um campo eletromagnético externo. A separação ocorre no momento em que o detector alcança ou no ângulo da curva no campo magnético, porque a massa do fragmento é maior e sua carga é menor, mais desajeitado. Assim, o espectrômetro de massa "pesa" as massas de fragmentos. Além disso, a "pesagem" pode ser feita em etapas, filtrando repetidamente fragmentos com a mesma massa (mais precisamente, com um valor

$ inline $ m / z $ inline $ ) e conduzi-los através da fragmentação com mais separação. Os espectrômetros de massa de dois estágios são amplamente distribuídos e são chamados espectrômetros de massa em tandem, os espectrômetros de massa de vários estágios são extremamente raros e são simplesmente designados como

$ inline $ ms ^ n $ inline $ onde

$ inline $ n $ inline $ - o número de etapas. E aqui surge a tarefa: como, conhecendo apenas as massas de todos os tipos de fragmentos de qualquer molécula, conhecer sua estrutura? Então, chegamos a problemas nas estradas e nas vias principais, para peptídeos lineares e cíclicos, respectivamente.Explicarei com mais detalhes como a tarefa de restaurar a estrutura de uma biomolécula é reduzida aos problemas indicados usando o exemplo de um peptídeo cíclico.

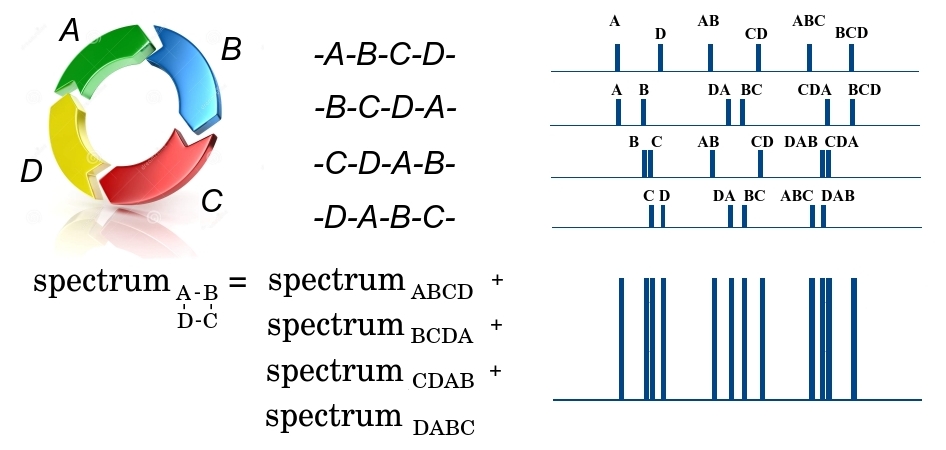
O peptídeo cíclico ABCD no primeiro estágio de fragmentação pode ser quebrado em 4 locais, por ligação DA, ou por AB, BC ou CD, formando 4 possíveis peptídeos lineares - ABCD, BCDA, CDAB ou DABC. Como um grande número de peptídeos idênticos passa pelo espectrômetro, teremos fragmentos de todos os 4 tipos na saída. Além disso, notamos que todos os fragmentos têm a mesma massa e não podem ser separados no primeiro estágio. No segundo estágio, o fragmento linear ABCD pode ser quebrado em três locais, formando fragmentos menores com diferentes massas A e BCD, AB e CD, ABC e D e formando o espectro de massa correspondente. Nesse espectro, a massa do fragmento é plotada ao longo do eixo x, e o número de pequenos fragmentos com uma dada massa ao longo do eixo y. Da mesma forma, os espectros são formados para os três fragmentos lineares restantes de BCDA, CDAB e DABC. Como todos os quatro fragmentos grandes passaram para o segundo estágio, todos os seus espectros são somados. Total, o resultado é alguma massa

$ inline $ \ {m_1 ^ {n_1}, m_2 ^ {n_2}, .., m_q ^ {n_q} \} $ inline $ onde

$ inline $ m_i $ inline $ - alguma massa, e

$ inline $ n_i $ inline $ - a frequência de sua repetição. Ao mesmo tempo, não sabemos a que fragmento essa massa pertence e se esse fragmento é único, pois fragmentos diferentes podem ter uma massa. Quanto mais as ligações no peptídeo estiverem uma da outra, maior a massa do fragmento peptídico está entre elas. Ou seja, a tarefa de restaurar a ordem dos elementos em um peptídeo cíclico reduz-se a um problema de canaleta, no qual os elementos do conjunto

$ inline $ X $ inline $ são ligações no peptídeo e elementos de uma multidão

$ inline $ \ Delta X $ inline $ - massas de fragmentos entre ligações.

Antecipação da existência de um algoritmo com tempo polinomial para a solução de problemas de via

Da minha própria experiência e da comunicação com pessoas que tentaram ou realmente fizeram algo para resolver esse problema, notei que a grande maioria das pessoas tenta resolvê-lo no caso geral ou para dados inteiros em um intervalo estreito, como este (1, 50) Ambas as opções estão fadadas ao fracasso. Para o caso geral, ficou provado que o número total de soluções para problemas de via no caso unidimensional

$ inline $ S_1 (n) $ inline $ limitado por valores (Lemke, 2003)

$$ display $$ e ^ {2 ^ {\ frac {\ ln n} {\ ln \ ln n} + o (1)}} \ leq S_1 (n) \ leq \ frac {1} {2} n ^ {n-2} $$ exibir $$o que significa a presença de um número exponencial de soluções nos assintóticos

$ inline $ n \ rightarrow \ infty $ inline $ . Obviamente, se o número de soluções cresce exponencialmente, o tempo de recebimento não pode crescer mais lentamente. Ou seja, para o caso geral, é impossível obter uma solução de tempo polinomial. Quanto aos dados inteiros em um intervalo estreito, tudo pode ser verificado experimentalmente, pois não é muito difícil escrever código que procura uma solução por meio de uma pesquisa exaustiva. Para pequenas

$ inline $ n $ inline $ esse código não levará muito tempo. Os resultados do teste desse código mostrarão que, nessas condições de dados, o número total de soluções diferentes para qualquer conjunto

$ inline $ \ Delta X $ inline $ já em pequeno

$ inline $ n $ inline $ também crescendo extremamente acentuadamente.Tendo aprendido sobre esses fatos, você pode desistir dessa tarefa. Admito que essa seja uma das razões pelas quais o problema do anel viário ainda é considerado não resolvido. No entanto, existem brechas. Lembre-se de que a função exponencial

$ inline $ e ^ {\ alpha x} $ inline $ comporta-se muito interessante. A princípio, cresce muito lentamente, subindo de 0 para 1 em um intervalo infinitamente grande de

$ inline $ \ infty $ inline $ para 0, então seu crescimento acelera cada vez mais. No entanto, quanto menor o valor

$ inline $ \ alpha $ inline $ quanto maior o valor deve ser

$ inline $ x $ inline $ para que o resultado da função ultrapasse algum valor definido

$ inline $ y = \ xi $ inline $ . Como tal valor, é conveniente escolher um número

$ inline $ \ xi = 2 $ inline $ , diante dele a única solução, depois dele existem muitas decisões. Pergunta E alguém verificou a dependência do número de decisões sobre quais dados chegam à entrada? Sim eu fiz. Há uma maravilhosa dissertação de doutorado pela matemática croata Tamara Dakis (Dakic, 2000), na qual ela determinou quais condições os dados de entrada devem satisfazer para que o problema seja resolvido em tempo polinomial. O mais importante deles é a exclusividade da solução e a ausência de duplicação no conjunto de dados de entrada.

$ inline $ \ Delta X $ inline $ . O nível de sua dissertação de doutorado é muito alto. É lamentável que essa aluna tenha se limitado apenas a um problema na estrada, estou convencido de que, se ela tivesse se interessado pelo problema da via, isso teria sido resolvido há muito tempo.

Obtenção de um algoritmo com tempo polinomial resolvendo problemas de pista

Foi possível encontrar os dados para os quais é possível construir o algoritmo desejado por acaso. Foram necessárias idéias adicionais. A idéia principal surgiu da observação (veja acima) de que o espectro de um peptídeo cíclico é a soma dos espectros de todos os peptídeos lineares que são formados em quebras de anel simples. Como a sequência de aminoácidos em um peptídeo pode ser restaurada a partir de qualquer peptídeo linear, o número total de linhas no espectro é significativo (em

$ inline $ n $ inline $ vezes em que

$ inline $ n $ inline $ - o número de aminoácidos no peptídeo) é excessivo. A questão é apenas quais linhas devem ser excluídas do espectro para não perder a capacidade de restaurar a sequência. Como ambas as tarefas (restauração da sequência peptídica cíclica do problema do espectro de massa e da via) são matematicamente isomórficas, também é possível afinar muitas

$ inline $ \ Delta X $ inline $ .Operações de desbaste

$ inline $ \ Delta X $ inline $ foram construídas usando simetrias locais do conjunto

$ inline $ \ Delta X $ inline $ (Fomin, 2016a).

Simetrização A primeira operação é selecionar um elemento arbitrário do conjunto $ inline $ x _ {\ mu} \ in \ Delta X $ inline $ e remova de $ inline $ \ Delta X $ inline $ todos os elementos, exceto aqueles que possuem pares simétricos em relação aos pontos $ inline $ x _ {\ mu} / 2 $ inline $ e $ inline $ (L + x _ {\ mu}) / 2 $ inline $ onde $ inline $ L $ inline $ - circunferência (lembro-me que, no caso do anel viário, todos os pontos estão localizados no círculo).
Convolução parcial da solução. A segunda operação utiliza as suposições sobre a solução, ou seja, o conhecimento dos pontos individuais que pertencem à solução, a chamada solução parcial. De muitos $ inline $ \ Delta X $ inline $ todos os elementos também são excluídos, exceto aqueles que satisfazem a condição - se medirmos a distância do ponto que está sendo testado a todos os pontos de uma solução parcial, todos os valores obtidos estarão em $ inline $ \ Delta X $ inline $ . Esclarecerei que, se pelo menos uma das distâncias obtidas estiver ausente em $ inline $ \ Delta X $ inline $ então o ponto é ignorado.

Os teoremas foram provados que ambas as operações afinam o conjunto

$ inline $ \ Delta X $ inline $ , mas ainda há elementos suficientes para restaurar a solução

$ inline $ X $ inline $ . Usando essas operações, um algoritmo foi construído e implementado em c ++ para resolver o problema da via (Fomin, 2016b). O algoritmo difere pouco do algoritmo de backtracking clássico (ou seja, tentamos criar uma solução enumerando as opções possíveis e retornando se recebermos um erro durante a construção). A única diferença é que, para restringir o conjunto

$ inline $ \ Delta X $ inline $ nos testar se torna significativamente menos opções.Aqui está um exemplo de quantas

$ inline $ \ Delta X $ inline $ quando desbaste.

Experimentos computacionais foram realizados para peptídeos cíclicos gerados aleatoriamente

$ inline $ n $ inline $ de 10 a 1000 aminoácidos (o eixo das ordenadas em escala logarítmica). A abscissa também mostra em escala logarítmica o número de elementos nos conjuntos diluídos por várias operações

$ inline $ \ Delta X $ inline $ em unidades

$ inline $ n $ inline $ . Essa representação é absolutamente incomum; portanto, decifrarei como é lida em um exemplo. Nós olhamos para o diagrama esquerdo. Deixe o peptídeo ter um comprimento

$ inline $ n = 100 $ inline $ . Para ele, o número de elementos no conjunto

$ inline $ \ Delta X $ inline $ é igual a

$ inline $ n ^ 2 = 10000 $ inline $ (este é um ponto na linha tracejada superior

$ inline $ y = n ^ 2 $ inline $ ) Depois de remover do conjunto

$ inline $ \ Delta X $ inline $ repetindo elementos, número de elementos em

$ inline $ \ Delta X $ inline $ diminui para

$ inline $ n_D \ approx n ^ {1.9} \ aproximadamente 6300 $ inline $ (círculos com cruzes). Após a simetrização, o número de elementos cai para

$ inline $ n_S \ approx n ^ {1,75} \ aproximadamente 3100 $ inline $ (círculos pretos) e após convolução por solução parcial para

$ inline $ n_C \ approx n ^ {1.35} \ aproximadamente 500 $ inline $ (cruza). Total, o volume total do conjunto

$ inline $ \ Delta X $ inline $ reduzido em apenas 20 vezes. Para um peptídeo do mesmo comprimento, mas no diagrama correto, a contração vem de

$ inline $ n ^ 2 = 10000 $ inline $ antes

$ inline $ N_C \ aproximadamente n \ aproximadamente 100 $ inline $ , ou seja, 100 vezes.Observe que a geração de casos de teste para o diagrama esquerdo é executada para que o nível de duplicação

$ inline $ k_ {dup} $ inline $ em

$ inline $ \ Delta X $ inline $ estava na faixa de 0,1 a 0,3 e, à direita - menos de 0,1. O nível de duplicação é definido como

$ inline $ k_ {dup} = 2- \ log {N_u} / \ log {n} $ inline $ onde

$ inline $ N_u $ inline $ - o número de elementos únicos no conjunto

$ inline $ \ Delta X $ inline $ . Essa definição fornece um resultado natural: na ausência de duplicatas no conjunto

$ inline $ \ Delta X $ inline $ seu poder é igual

$ inline $ N_u = n ^ 2 $ inline $ e

$ inline $ k_ {dup} = 0 $ inline $ na duplicação máxima possível

$ inline $ N_u = n $ inline $ e

$ inline $ k_ {dup} = 1 $ inline $ . Como tornar possível fornecer um nível diferente de duplicação, direi um pouco mais tarde. Os diagramas mostram que quanto menor o nível de duplicação, mais fino

$ inline $ \ Delta X $ inline $ às

$ inline $ k_ {dup} <0,1 $ inline $ número de elementos em diluído

$ inline $ \ Delta X $ inline $ geralmente atinge seu limite

$ inline $ O (n ^ 2) \ rightarrow O (n) $ inline $ , já que no conjunto dizimado é menor que

$ inline $ O (n) $ inline $ elementos não podem ser obtidos (as operações armazenam elementos suficientes para obter uma solução na qual

$ inline $ n $ inline $ elementos). O fato de restringir o poder do conjunto

$ inline $ \ Delta X $ inline $ até o limite inferior é muito importante, é ele quem leva a mudanças drásticas na complexidade computacional da obtenção de uma solução.Depois de inserir as operações de desbaste no algoritmo de retorno e resolver o problema da pista, foi revelado um análogo completo do que Tamara Dakis falou sobre o problema da rodovia. Deixe-me lembrá-lo. Ela disse que, para problemas de pedágio, é possível obter uma solução em tempo polinomial se a solução for única e não houver duplicação de

$ inline $ \ Delta X $ inline $ . Verificou-se que uma ausência completa de duplicação não é necessária (dificilmente é possível para dados reais), basta que seu nível seja bastante pequeno. A figura abaixo mostra quanto tempo é necessário para obter uma solução do problema da via, dependendo do comprimento do peptídeo e do nível de duplicação em

$ inline $ \ Delta X $ inline $ .

Na figura, a abscissa e a ordenada são dadas em uma escala logarítmica. Isso permite que você veja claramente se a dependência do tempo de contagem no comprimento da sequência

$ inline $ T = f (n) $ inline $ exponencial (linha reta) ou polinomial (curva em forma de log). Como pode ser visto nos diagramas, com baixo nível de duplicação (diagrama à direita), a solução é obtida em tempo polinomial. Bem, para ser mais preciso, a solução é obtida em tempo quadrático. Isso ocorre quando as operações de desbaste reduzem a potência do aparelho para um limite inferior.

O(n^2) \rightarrow O(n)

Sobre a resolubilidade de problemas na via em tempo polinomial

Importância da resolução de problemas de via em termos de bioinformática

Antecipação da existência de um algoritmo com tempo polinomial para a solução de problemas de via

Obtenção de um algoritmo com tempo polinomial resolvendo problemas de pista

More articles: