Implementação do algoritmo k-means (k-means) usando o exemplo de trabalho com pixels

Olá pessoal! Recentemente, foi necessário escrever um código para implementar a segmentação de imagens usando o método k-means (inglês k-means). Bem, a primeira coisa que o Google faz é ajudar. Encontrei muitas informações, como do ponto de vista matemático (todos os tipos de rabiscos matemáticos complexos lá, você entenderá o que diabos está escrito lá), bem como algumas implementações de software que estão na Internet em inglês. Esses códigos são certamente bonitos - sem dúvida, mas a essência da idéia é difícil de entender. De alguma forma, é tudo complicado lá, confuso e, no entanto, manualmente, manualmente, você não escreve o código, não entende nada. Neste artigo, quero mostrar uma implementação simples, não produtiva, mas, espero, compreensível desse maravilhoso algoritmo. Ok, vamos lá!

Então, o que é agrupar em termos de nossas percepções? Deixe-me dar um exemplo, digamos que há uma bela foto com flores do chalé da sua avó.



A questão é: determinar quantas áreas nesta foto são preenchidas aproximadamente com a mesma cor. Bem, não é nada difícil: pétalas brancas - uma, centros amarelos - duas (não sou bióloga, não sei como se chamam), três verdes. Essas seções são chamadas de clusters. Um cluster é uma combinação de dados com recursos comuns (cor, posição etc.). O processo de determinar e colocar cada componente de qualquer dado em tais clusters - seções é chamado de cluster.

Existem muitos algoritmos de agrupamento, mas o mais simples deles é o k - médio, que será discutido mais adiante. O K-means é um algoritmo simples e eficiente, fácil de implementar usando um método de software. Os dados que iremos distribuir em clusters são pixels. Como você sabe, um pixel colorido possui três componentes - vermelho, verde e azul. A imposição desses componentes e cria uma paleta de cores existentes.



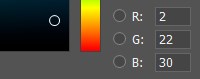
Na memória do computador, cada componente de cor é caracterizado por um número de 0 a 255. Ou seja, combinando diferentes valores de vermelho, verde e azul, obtemos uma paleta de cores na tela.

Usando pixels como exemplo, implementamos nosso algoritmo. K-means é um algoritmo iterativo, ou seja, fornecerá o resultado correto após um certo número de repetições de alguns cálculos matemáticos.

Algoritmo

1. Você precisa saber com antecedência quantos clusters precisa distribuir os dados. Essa é uma desvantagem significativa desse método, mas esse problema é resolvido por implementações aprimoradas do algoritmo, mas isso, como se costuma dizer, é uma história completamente diferente.
2. Precisamos escolher os centros iniciais de nossos clusters. Como Sim aleatoriamente. Porque Para que você possa encaixar cada pixel no centro do cluster. O centro é como o rei, em torno do qual seus súditos estão reunidos - pixels. É a “distância” do centro ao pixel que determina a quem cada pixel obedecerá.
3. Calculamos a distância de cada centro a cada pixel. Essa distância é considerada como a distância euclidiana entre pontos no espaço e, no nosso caso, como a distância entre os três componentes de cores:

   $$$$ display $$ \ sqrt {(R_ {2} -R_ {1}) ^ 2 + (G_ {2} -G_ {1}) ^ 2 + (B_ {2} -B_ {1}) ^ 2} . $$ display $$

   Calculamos a distância do primeiro pixel a cada centro e determinamos a menor distância entre esse pixel e os centros. Para o centro, a distância para a menor, recalculamos as coordenadas como a média aritmética entre cada componente do pixel - o rei e o pixel - o sujeito. Nosso centro muda no espaço de acordo com os cálculos.
4. Depois de contar todos os centros, distribuímos os pixels em grupos, comparando a distância de cada pixel aos centros. Um pixel é colocado em um cluster, ao centro do qual está mais próximo do que aos outros centros.
5. Tudo começa novamente, desde que os pixels permaneçam nos mesmos clusters. Frequentemente, isso pode não acontecer, uma vez que, com uma grande quantidade de dados, os centros se movem em um pequeno raio e os pixels ao longo das bordas dos clusters saltam para um ou outro cluster. Para fazer isso, determine o número máximo de iterações.

Implementação

Vou implementar este projeto em C ++. O primeiro arquivo é "k_means.h", nele eu defini os principais tipos de dados, constantes e a classe principal para trabalhar - "K_means".
Para caracterizar cada pixel, crie uma estrutura que consiste em três componentes de pixel, para os quais escolhi o tipo duplo para cálculos mais precisos e também determinei algumas constantes para o programa funcionar:

const int KK = 10; //  const int max_iterations = 100; //   typedef struct { double r; double g; double b; } rgb; 

A própria classe K_means:

 class K_means { private: std::vector<rgb> pixcel; int q_klaster; int k_pixcel; std::vector<rgb> centr; void identify_centers(); inline double compute(rgb k1, rgb k2) { return sqrt(pow((k1.r - k2.r),2) + pow((k1.g - k2.g), 2) + pow((k1.b - k2.b), 2)); } inline double compute_s(double a, double b) { return (a + b) / 2; }; public: K_means() : q_klaster(0), k_pixcel(0) {}; K_means(int n, rgb *mas, int n_klaster); K_means(int n_klaster, std::istream & os); void clustering(std::ostream & os); void print()const; ~K_means(); friend std::ostream & operator<<(std::ostream & os, const K_means & k); }; 

Vamos examinar os componentes da classe:

vectorpixcel - um vetor para pixels;
q_klaster - número de clusters;
k_pixcel - número de pixels;
vectorcentr - um vetor para centros de agrupamento, o número de elementos nele é determinado por q_klaster;
identity_centers () - um método para selecionar aleatoriamente os centros iniciais entre os pixels de entrada;
compute () e compute_s () são métodos internos para calcular a distância entre pixels e centros de recálculo, respectivamente;
três construtores: o primeiro é por padrão, o segundo é para inicializar pixels de uma matriz, o terceiro é para inicializar pixels de um arquivo de texto (na minha implementação, o arquivo é acidentalmente preenchido com dados no início e, em seguida, os pixels são lidos nesse arquivo para o programa funcionar, por que não diretamente no vetor - apenas necessário no meu caso);
clustering (std :: ostream & os) - método de clustering;
método e sobrecarga da instrução de saída para publicar os resultados.

Implementação do método:

 void K_means::identify_centers() { srand((unsigned)time(NULL)); rgb temp; rgb *mas = new rgb[q_klaster]; for (int i = 0; i < q_klaster; i++) { temp = pixcel[0 + rand() % k_pixcel]; for (int j = i; j < q_klaster; j++) { if (temp.r != mas[j].r && temp.g != mas[j].g && temp.b != mas[j].b) { mas[j] = temp; } else { i--; break; } } } for (int i = 0; i < q_klaster; i++) { centr.push_back(mas[i]); } delete []mas; } 

Este é um método para selecionar os centros de armazenamento em cluster inicial e adicioná-los ao vetor central. É realizada uma verificação para repetir os centros e substituí-los nesses casos.

 K_means::K_means(int n, rgb * mas, int n_klaster) { for (int i = 0; i < n; i++) { pixcel.push_back(*(mas + i)); } q_klaster = n_klaster; k_pixcel = n; identify_centers(); } 

Uma implementação de construtor para inicializar pixels de uma matriz.

 K_means::K_means(int n_klaster, std::istream & os) : q_klaster(n_klaster) { rgb temp; while (os >> temp.r && os >> temp.g && os >> temp.b) { pixcel.push_back(temp); } k_pixcel = pixcel.size(); identify_centers(); } 

Passamos um objeto de entrada para esse construtor para poder inserir dados do arquivo e do console.

 void K_means::clustering(std::ostream & os) { os << "\n\n :" << std::endl; /*             :        ,    -  ,    ,   ,        .*/ std::vector<int> check_1(k_pixcel, -1); std::vector<int> check_2(k_pixcel, -2); int iter = 0; /* .*/ while(true) { os << "\n\n----------------  №" << iter << " ----------------\n\n"; { for (int j = 0; j < k_pixcel; j++) { double *mas = new double[q_klaster]; /*  :          .      ,   .*/ for (int i = 0; i < q_klaster; i++) { *(mas + i) = compute(pixcel[j], centr[i]); os << "   " << j << "   #" << i << ": " << *(mas + i) << std::endl; } /*     m_k      .*/ double min_dist = *mas; int m_k = 0; for (int i = 0; i < q_klaster; i++) { if (min_dist > *(mas + i)) { min_dist = *(mas + i); m_k = i; } } os << "    #" << m_k << std::endl; os << "  #" << m_k << ": "; centr[m_k].r = compute_s(pixcel[j].r, centr[m_k].r); centr[m_k].g = compute_s(pixcel[j].g, centr[m_k].g); centr[m_k].b = compute_s(pixcel[j].b, centr[m_k].b); os << centr[m_k].r << " " << centr[m_k].g << " " << centr[m_k].b << std::endl; delete[] mas; } /*   .*/ int *mass = new int[k_pixcel]; os << "\n  : "<< std::endl; for (int k = 0; k < k_pixcel; k++) { double *mas = new double[q_klaster]; /*    .*/ for (int i = 0; i < q_klaster; i++) { *(mas + i) = compute(pixcel[k], centr[i]); os << "   №" << k << "   #" << i << ": " << *(mas + i) << std::endl; } /*  .*/ double min_dist = *mas; int m_k = 0; for (int i = 0; i < q_klaster; i++) { if (min_dist > *(mas + i)) { min_dist = *(mas + i); m_k = i; } } mass[k] = m_k; os << " №" << k << "     #" << m_k << std::endl; } /*            .*/ os << "\n    : \n"; for (int i = 0; i < k_pixcel; i++) { os << mass[i] << " "; check_1[i] = *(mass + i); } os << std::endl << std::endl; os << " : " << std::endl; int itr = KK + 1; for (int i = 0; i < q_klaster; i++) { os << " #" << i << std::endl; for (int j = 0; j < k_pixcel; j++) { if (mass[j] == i) { os << pixcel[j].r << " " << pixcel[j].g << " " << pixcel[j].b << std::endl; mass[j] = ++itr; } } } delete[] mass; /*    .*/ os << " : \n" ; for (int i = 0; i < q_klaster; i++) { os << centr[i].r << " " << centr[i].g << " " << centr[i].b << " - #" << i << std::endl; } } /*         –  .*/ iter++; if (check_1 == check_2 || iter >= max_iterations) { break; } check_2 = check_1; } os << "\n\n ." << std::endl; } 

O principal método de agrupamento.

 std::ostream & operator<<(std::ostream & os, const K_means & k) { os << " : " << std::endl; for (int i = 0; i < k.k_pixcel; i++) { os << k.pixcel[i].r << " " << k.pixcel[i].g << " " << k.pixcel[i].b << " - №" << i << std::endl; } os << std::endl << "   : " << std::endl; for (int i = 0; i < k.q_klaster; i++) { os << k.centr[i].r << " " << k.centr[i].g << " " << k.centr[i].b << " - #" << i << std::endl; } os << "\n : " << k.q_klaster << std::endl; os << " : " << k.k_pixcel << std::endl; return os; } 

A saída dos dados iniciais.

Exemplo de saída

Este exemplo é planejado com antecedência, os pixels são selecionados especificamente para demonstração. Duas iterações são suficientes para o programa agrupar os dados em três clusters. Observando os centros das duas últimas iterações, é possível ver que elas praticamente permaneceram no lugar.

Mais interessantes são os casos de pixels gerados aleatoriamente. Tendo gerado 50 pontos que precisam ser divididos em 10 grupos, obtive 5 iterações. Tendo gerado 50 pontos que precisam ser divididos em 3 grupos, obtive todas as 100 iterações máximas permitidas. Você pode perceber que quanto mais clusters, mais fácil é para o programa encontrar os pixels mais semelhantes e combiná-los em grupos menores, e vice-versa - se houver poucos clusters e muitos pontos, o algoritmo geralmente termina apenas quando o número máximo de iterações é excedido, pois alguns pixels saltam constantemente de um cluster para outro. No entanto, o volume ainda é determinado em seus clusters completamente.

Bem, agora vamos verificar o resultado do armazenamento em cluster. Tomando o resultado de alguns clusters do exemplo de 50 pontos por 10 clusters, direcionei o resultado desses dados para o Illustrator e foi o que aconteceu:



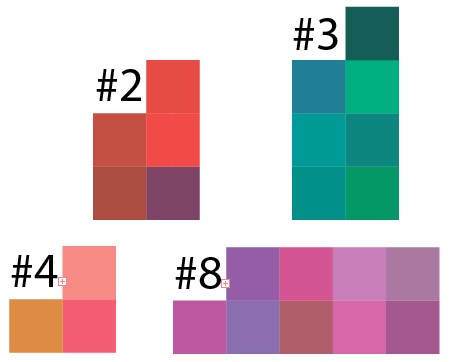
Pode-se observar que em cada cluster prevalece qualquer tom de cor, e aqui você precisa entender que os pixels foram selecionados aleatoriamente, o análogo dessa imagem na vida real é algum tipo de imagem na qual todas as cores foram acidentalmente pulverizadas e é difícil selecionar áreas de cores semelhantes.

Digamos que temos uma foto assim. Podemos definir uma ilha como um aglomerado, mas, com um aumento, vemos que ela consiste em diferentes tons de verde.



E este é o cluster 8, mas em uma versão menor, o resultado é semelhante:



A versão completa do programa pode ser visualizada no meu GitHub .