Matemática divertida. O sistema numérico mais econômico

Todos nós sabemos pelo curso da escola qual é o sistema numérico (SS). Mas nem todo mundo pensa em quanto a SS é. I.e. que conjunto de números precisamos representar o número nesta SS. Quando temos um conjunto limitado de elementos únicos (seixos multicoloridos de tamanhos diferentes) com os quais podemos representar um número, qual é o número máximo que podemos representar usando esses elementos? (todos os seixos vermelhos são zero, verde é um, azul são dois, etc., pequenos são zero, médios são primeiro, grandes são segundo, etc.). Onde está a linha na qual a base da SS desempenha um papel maior que a capacidade de dígitos do número?

Tomemos, por exemplo, n - o número de elementos igual a 60. Depois de dividir os elementos em 2 grupos (sistema de números binários), obtemos 30 dígitos. 30 unidades é o maior número de 30 bits com uma base de 2. Se você adicionar 1, obterá uma unidade com 30 zeros, ou seja, 2 no dia 30, uma vez que cada zero é uma potência de dois, e os dígitos começam em 0 e não se esqueça de subtrair a unidade que foi adicionada.

Para outros SSs, da mesma forma $$$y = x ^ {60 / x} -1$onde y é o número máximo, x é a base do grau.

Pontos de construção:

$$$2 ^ {30} -1 = 1 \, 073 \, 741 \, 823$.
$$$3 ^ {20} -1 = 3 \, 486 \, 784 \, 400$.
$$$4 ^ {15} -1 = 1 \, 073 \, 741 \, 823$
$$$5 ^ {12} -1 = 244 \, 140 \, 624$
$$$6 ^ {10} -1 = 60 \, 466 \, $ 17$
$$$10 ^ {6} -1 = 999 \, $ 99$
$$$12 ^ {5} -1 = 248 \, $ 83$

Gráfico de funções:



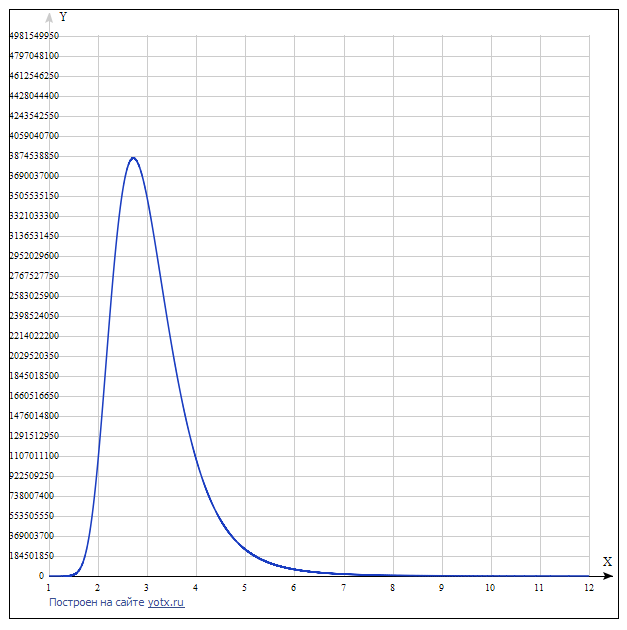
O gráfico mostra que, com um aumento na base da SS, começando com três, seu custo aumenta e a função possui um extremo superior. Trazendo-o para uma forma geral, você pode obter $$$y = (\ sqrt [x] x) ^ {n} -1$e a função máxima $$$\ sqrt [x] x$alcançado quando $$$x = e$.



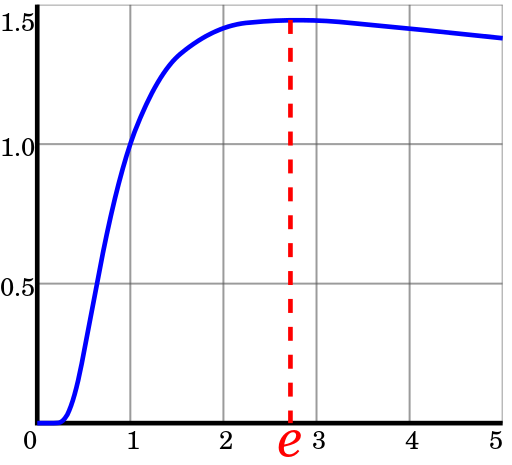
Gráfico de funções $$$y = \ sqrt [x] x$

I.e. o SS mais econômico é um sistema o mais próximo possível $$$e$ou 3.

PS: Além disso, o SS com base 3 é ímpar, o que significa que ele não tem um problema de arredondamento (leve 0,5 para 0 ou 1) e, se os números forem escritos simetricamente (-1,0.1 em vez de 0.1.2), a simplicidade aparecerá representa números negativos (10-1 é 8, -101 é -8, onde menos não é um sinal, mas parte de um dígito que pode ser substituído por Z), mas essa é uma aritmética completamente diferente)))