Como tornar ainda mais estados inválidos ainda mais indizíveis

Há pouco tempo, um artigo foi traduzido na Habr sobre como usar tipos de dados algébricos para garantir que estados incorretos sejam inexprimíveis. Hoje, olhamos para uma maneira um pouco mais generalizada, escalável e segura de expressar o inexprimível, e o Haskell nos ajudará nisso.

Em resumo, esse artigo discute alguma entidade com um endereço para correspondência e um endereço de email, além da condição adicional de que deve haver pelo menos um desses endereços. Como é proposto expressar essa condição no nível de tipo? Propõe-se escrever os endereços da seguinte maneira:

type ContactInfo = | EmailOnly of EmailContactInfo | PostOnly of PostalContactInfo | EmailAndPost of EmailContactInfo * PostalContactInfo 

Que problemas essa abordagem tem?

O mais óbvio (e observado várias vezes nos comentários sobre esse artigo) é que essa abordagem não é escalável. Imagine que não temos dois tipos de endereços, mas três ou cinco, e a condição de correção parece "deve haver um endereço para correspondência, ou um endereço de e-mail e um endereço comercial, e não deve haver vários endereços do mesmo tipo". Aqueles que desejam podem escrever o tipo apropriado como um exercício para autoteste. A tarefa com um asterisco é reescrever esse tipo no caso em que a condição sobre a ausência de duplicatas desapareceu do TOR.

Compartilhar

Como resolver este problema? Vamos tentar fantasiar. Primeiro decompomos e separamos a classe de endereço (por exemplo, número de email / email / mesa no escritório) e o conteúdo correspondente a essa classe:

 data AddrType = Post | Email | Office 

Ainda não pensamos no conteúdo, porque não há nada nos termos de referência para a validade da lista de endereços.

Se verificássemos a condição correspondente no tempo de execução de algum construtor de alguma linguagem OOP comum, simplesmente escreveríamos uma função como

 valid :: [AddrType] -> Bool valid xs = let hasNoDups = nub xs == xs --      hasPost = Post `elem` xs hasEmail = Email `elem` xs hasOffice = Office `elem` xs in hasNoDups && (hasPost || (hasEmail && hasOffice)) 

e lançaria alguma execução se retornar False .

Em vez disso, podemos verificar uma condição semelhante com a ajuda de um cronômetro ao compilar? Acontece que sim, podemos, se o sistema de tipos da linguagem for expressivo o suficiente, e no restante do artigo, escolheremos essa abordagem.

Aqui os tipos dependentes nos ajudarão bastante, e como a maneira mais adequada de escrever um código validado no Haskell é escrevê-lo primeiro no Agde ou no Idris, trocaremos de sapatos e escreveremos no Idris. A sintaxe idris está bem próxima do Haskell: por exemplo, com a função mencionada acima, você só precisa alterar ligeiramente a assinatura:

 valid : List AddrType -> Bool 

Agora lembre-se de que, além das classes de endereço, também precisamos do conteúdo e codificamos a dependência dos campos na classe de endereço como GADT:

 data AddrFields : AddrType -> Type where PostFields : (city : String) -> (street : String) -> AddrFields Post EmailFields : (email : String) -> AddrFields Email OfficeFields : (floor : Int) -> (desk : Nat) -> AddrFields Office 

Ou seja, se AddrFields t um valor de fields tipo AddrFields t , saberemos que t é uma AddrType AddrType e que esses fields contêm um conjunto de campos correspondentes a essa classe específica.

 addrFields : AddrType -> Type addrFields Post = PostFields addrFields Email = EmailFields addrFields Office = OfficeFields 

Qual é o endereço completo neste modelo? Este é um par da classe de endereço e dos campos correspondentes:

 Addr : Type Addr = (t : AddrType ** AddrFields t) 

Os fãs da teoria dos tipos dirão que este é um tipo dependente existencial: se AddrType algum valor do tipo Addr , isso significa que existe um valor t tipo AddrType e um conjunto correspondente de campos AddrFields t . Naturalmente, endereços de uma classe diferente são do mesmo tipo:

 someEmailAddr : Addr someEmailAddr = (Email ** EmailFields "that@feel.bro") someOfficeAddr : Addr someOfficeAddr = (Office ** OfficeFields (-2) 762) 

Além disso, se EmailFields for fornecido, a única classe de endereço adequada é o Email , para que você possa omiti-lo, o timer o imprimirá você mesmo:

 someEmailAddr : Addr someEmailAddr = (_ ** EmailFields "that@feel.bro") someOfficeAddr : Addr someOfficeAddr = (_ ** OfficeFields (-2) 762) 

Escrevemos uma função auxiliar que fornece a lista correspondente de classes de endereço da lista de endereços e a generalizamos imediatamente para trabalhar em um functor arbitrário:

 types : Functor f => f Addr -> f AddrType types = map fst 

Aqui, o tipo Addr existencial se comporta como um casal familiar: em particular, você pode solicitar seu primeiro componente AddrType (tarefa com um asterisco: por que não posso solicitar o segundo componente?).

Aumentar

Agora passamos para uma parte essencial da nossa história. Portanto, temos uma lista de endereços de valid : List AddrType -> Bool List Addr e algum predicado valid : List AddrType -> Bool , cuja execução dessa lista queremos garantir no nível dos tipos. Como os combinamos? Claro, outro tipo!

 data ValidatedAddrList : List Addr -> Type where MkValidatedAddrList : (lst : List Addr) -> (prf : valid (types lst) = True) -> ValidatedAddrList lst 

Agora vamos analisar o que escrevemos aqui.

data ValidatedAddrList : List Addr -> Type where significa que o tipo ValidatedAddrList parametrizado, de fato, pela lista de endereços.

Vejamos a assinatura do único construtor MkValidatedAddrList desse tipo: (lst : List Addr) -> (prf : valid (types lst) = True) -> ValidatedAddrList lst . Ou seja, é necessária uma lista de endereços lst e outro argumento prf do tipo valid (types lst) = True . O que esse tipo significa? Portanto, significa que o valor à esquerda de = é igual ao valor à direita de = , ou seja, valid (types lst) , de fato, é True.

Como isso funciona? Assinatura = parece (x : A) -> (y : B) -> Type . Ou seja, = assume dois valores arbitrários x e y (possivelmente até de tipos diferentes A e B , o que significa que a desigualdade nos idris é heterogênea e que é um tanto ambígua do ponto de vista da teoria dos tipos, mas esse é um tópico para outra discussão). O que então demonstra igualdade? E devido ao fato de que o único construtor = - Refl com uma assinatura de quase (x : A) -> x = x . Ou seja, se tivermos um valor do tipo x = y , sabemos que ele foi construído usando Refl (porque não há outros construtores), o que significa que x é realmente igual a y .

Observe que é por isso que, no Haskell, sempre fingimos que estamos provando alguma coisa, porque o Haskell undefined que habita qualquer tipo, de modo que o argumento acima não funciona lá: para qualquer x , y termo do tipo x = y pode ser criado via undefined (ou através de recursão infinita, digamos que em geral seja o mesmo em termos de teoria de tipos).

Também observamos que a igualdade aqui não é significada no sentido de Haskell Eq ou algum operator== em C ++, mas muito mais rigorosa: estrutural, que, simplificando, significa que os dois valores têm a mesma forma . Ou seja, enganá-lo de forma simples não funciona. Mas questões de igualdade são tradicionalmente atraídas para um artigo separado.

Para consolidar nossa compreensão da igualdade, escrevemos testes de unidade para a função valid :

 testPostValid : valid [Post] = True testPostValid = Refl testEmptyInvalid : valid [] = False testEmptyInvalid = Refl testDupsInvalid : valid [Post, Post] = False testDupsInvalid = Refl testPostEmailValid : valid [Post, Email] = True testPostEmailValid = Refl 

Esses testes são bons porque você nem precisa executá-los, basta que o taypcher os tenha verificado. De fato, vamos substituir True por False , por exemplo, no primeiro deles e ver o que acontece:

 testPostValid : valid [Post] = False testPostValid = Refl 

Typsekher jura

como esperado. Ótimo

Simplifique

Agora vamos refatorar nosso ValidatedAddrList pouco.

Em primeiro lugar, o padrão de comparação de um determinado valor com True bastante comum; portanto, existe um tipo especial So nos idris: você pode usar So x como sinônimo de x = True . Vamos corrigir a definição de ValidatedAddrList :

 data ValidatedAddrList : List Addr -> Type where MkValidatedAddrList : (lst : List Addr) -> (prf : So (valid $ types lst)) -> ValidatedAddrList lst 

Além disso, o So tem uma função auxiliar conveniente, que em essência eleva a verificação ao nível dos tipos:

 > :doc choose Data.So.choose : (b : Bool) -> Either (So b) (So (not b)) Perform a case analysis on a Boolean, providing clients with a So proof 

Será útil quando escrevermos funções que modificam esse tipo.

Em segundo lugar, algumas vezes (especialmente no desenvolvimento interativo) os idris podem encontrar o valor apropriado de prf conta própria. Para que, nesses casos, não fosse necessário construí-lo manualmente, existe um açúcar sintático correspondente:

 data ValidatedAddrList : List Addr -> Type where MkValidatedAddrList : (lst : List Addr) -> {auto prf : So (valid $ types lst)} -> ValidatedAddrList lst 

Aparelhos encaracolados significam que este é um argumento implícito que idris tentará sair do contexto, e auto significa que ele também tentará construí-lo.

Então, o que esse novo ValidatedAddrList nos fornece? E isso fornece uma cadeia de raciocínio: seja val um valor do tipo ValidatedAddrList lst . Isso significa que lst é uma lista de endereços e, além disso, val foi criado usando o construtor MkValidatedAddrList , para o qual passamos esse muito lst e outro valor prf do tipo So (valid $ types lst) , que é quase valid (types lst) = True . E para que possamos construir o prf , precisamos, de fato, provar que essa igualdade é válida.

E o mais bonito é que tudo isso é verificado por um tympher. Sim, a verificação de validade terá que ser feita em tempo de execução (porque os endereços podem ser lidos a partir de um arquivo ou da rede), mas o cronômetro garantirá que essa verificação seja feita: sem ela, você não pode criar um ValidatedAddrList . Pelo menos em idris. Em Haskell, infelizmente.

Inserir

Para verificar a inevitabilidade da verificação, tentaremos escrever uma função para adicionar um endereço à lista. Primeira tentativa:

 insert : (addr : Addr) -> ValidatedAddrList lst -> ValidatedAddrList (addr :: lst) insert addr (MkValidatedAddrList lst) = MkValidatedAddrList (addr :: lst) 

Não, o erro de digitação dá nos dedos (embora não seja muito legível, o custo da valid muito complicado):

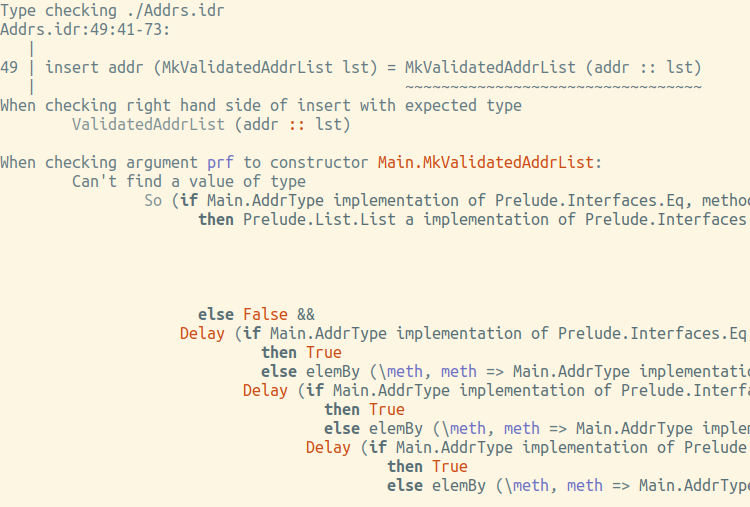
Como conseguimos uma cópia deste So ? Nada além da choose mencionada acima. Segunda tentativa:

 insert : (addr : Addr) -> ValidatedAddrList lst -> ValidatedAddrList (addr :: lst) insert addr (MkValidatedAddrList lst) = case choose (valid $ types (addr :: lst)) of Left l => MkValidatedAddrList (addr :: lst) Right r => ?rhs 

É quase typechetsya. "Quase" porque não está claro o que substituir por rhs . Pelo contrário, é claro: neste caso, a função deve de alguma forma relatar um erro. Portanto, você precisa alterar a assinatura e agrupar o valor de retorno, por exemplo, em Maybe :

 insert : (addr : Addr) -> ValidatedAddrList lst -> Maybe (ValidatedAddrList (addr :: lst)) insert addr (MkValidatedAddrList lst) = case choose (valid $ types (addr :: lst)) of Left l => Just $ MkValidatedAddrList (addr :: lst) Right r => Nothing 

Isso é lado a lado e funciona como deveria.

Mas agora surge o seguinte problema não muito óbvio, que estava, de fato, no artigo original. O tipo desta função não para de escrever essa implementação:

 insert : (addr : Addr) -> ValidatedAddrList lst -> Maybe (ValidatedAddrList (addr :: lst)) insert addr (MkValidatedAddrList lst) = Nothing 

Ou seja, sempre dizemos que não conseguimos criar uma nova lista de endereços. Typhechaetsya? Sim Está correto? Bem, dificilmente. Isso pode ser evitado?

Acontece que é possível, e temos todas as ferramentas necessárias para isso. Se for bem-sucedido, insert retorna um ValidatedAddrList , que contém evidências desse mesmo sucesso. Portanto, adicione simetria elegante e peça à função que retorne também uma prova de falha!

 insert : (addr : Addr) -> ValidatedAddrList lst -> Either (So (not $ valid $ types (addr :: lst))) (ValidatedAddrList (addr :: lst)) insert addr (MkValidatedAddrList lst) = case choose (valid $ types (addr :: lst)) of Left l => Right $ MkValidatedAddrList (addr :: lst) Right r => Left r 

Agora não podemos simplesmente pegar e sempre retornar Nothing .

Você pode fazer o mesmo para funções de remoção de endereço e similares.

Vamos ver como agora tudo parece no final.

Vamos tentar criar uma lista de endereços vazia:

É impossível, uma lista vazia não é válida.

Que tal uma lista de apenas um endereço para correspondência?

Ok, vamos tentar inserir o endereço para correspondência na lista que já possui o endereço para correspondência:

Vamos tentar inserir o email:

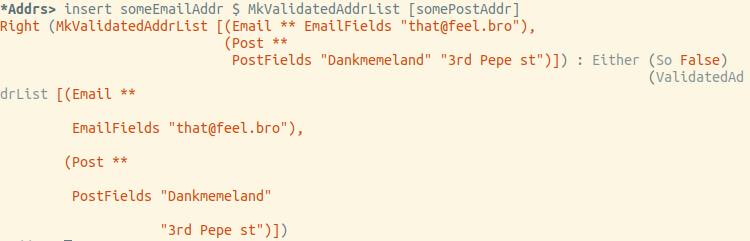
No final, tudo funciona exatamente como o esperado.

Ufa. Eu pensei que seriam três linhas, mas acabou um pouco mais. Para explorar até onde podemos chegar no Haskell, estaremos no próximo artigo. Enquanto isso, um pouco

Ponderar

No final, qual é o lucro dessa decisão em comparação com o dado no artigo, a que nos referimos no início?

1. Novamente, é muito mais escalável. Funções de validação complexas são mais fáceis de escrever.
2. É mais isolado. O código do cliente não precisa saber o que está dentro da função de validação, enquanto o formulário ContactInfo do artigo original exige que ele esteja vinculado.
3. A lógica de validação é escrita na forma de funções comuns e familiares, para que possa ser verificada imediatamente com leitura cuidadosa e testada com testes de tempo de compilação, em vez de derivar o significado da validação de um formulário de tipo de dados que representa um resultado já verificado.
4. Torna-se possível especificar com mais precisão o comportamento das funções que funcionam com o tipo de dados de seu interesse, principalmente no caso de falha na aprovação no teste. Por exemplo, a insert gravada como resultado é simplesmente impossível escrever incorretamente . Da mesma forma, pode-se escrever insertOrReplace , insertOrIgnore e similares, cujo comportamento é totalmente especificado no tipo.

Qual é o lucro comparado a uma solução de POO como essa?

 class ValidatedAddrListClass { public: ValidatedAddrListClass(std::vector<Addr> addrs) { if (!valid(addrs)) throw ValidationError {}; } }; 

1. O código é mais modularizado e seguro. No caso acima, uma verificação é uma ação que é verificada uma vez e sobre a qual eles se esqueceram posteriormente. Tudo se baseia na honestidade e no entendimento de que, se você possui um ValidatedAddrListClass , sua implementação fez uma verificação lá. O fato dessa verificação da classe não pode ser escolhido como um determinado valor. No caso de um valor de algum tipo, esse valor pode ser transferido entre diferentes partes do programa, usado para criar valores mais complexos (por exemplo, novamente, negar essa verificação), investigar (consulte o próximo parágrafo) e geralmente fazer o mesmo que costumávamos fazer. com valores.
2. Tais verificações podem ser usadas na correspondência de padrões (dependente). É verdade que não no caso dessa função valid e nem no caso de idris, é dolorosamente complicado e idris é dolorosamente monótono para que informações úteis para padrões possam ser extraídas da estrutura valid . No entanto, valid pode ser reescrito em um estilo de correspondência de padrões um pouco mais amigável, mas isso está além do escopo deste artigo e geralmente não é trivial por si só.

Quais são as desvantagens?

Vejo apenas uma falha fundamental séria: valid é uma função estúpida demais. Ele retorna apenas um bit de informação - se os dados passaram na validação ou não. No caso de tipos mais inteligentes, poderíamos conseguir algo mais interessante.

Por exemplo, imagine que o requisito de exclusividade de endereços desapareceu do TK. Nesse caso, é óbvio que adicionar um novo endereço à lista de endereços existente não tornará a lista inválida; portanto, poderíamos provar esse teorema escrevendo uma função com o tipo So (valid $ types lst) -> So (valid $ types $ addr :: lst) e use-o, por exemplo, para escrever com segurança de tipo sempre bem-sucedida

 insert : (addr : Addr) -> ValidatedAddrList lst -> ValidatedAddrList (addr :: lst) 

Mas, infelizmente, teoremas como recursão e indução, e nosso problema não possui nenhuma estrutura indutiva elegante; portanto, na minha opinião, o código com o valor booleano de carvalho valid também valid bom.