Neste artigo, criaremos um modelo de controlador baseado na biblioteca padrão de modelagem estrutural (sem usar uma biblioteca pronta de blocos de regulação nebulosos).
Como objeto de controle, um modelo de um motor de turbina a gás do livro de texto de V.I. Gosteva “Reguladores difusos em sistemas de controle automático”
Vamos fazer uma comparação com os reguladores PID e SDA.
Declaração do problema
A diferença entre um motor de turbina a gás (motor de turbina a gás) e um motor de turbojato (motor de turbojato) é que, em um motor de turbina a gás, toda a energia é removida através do eixo. Nos motores de turbojato, a energia é liberada na forma de um jato.
Os motores de turbina a gás (GTE) são amplamente utilizados nas indústrias de gás e aviação, onde são a base de unidades de bombeamento de gás e usinas de aeronaves, em acionamentos de turbogeradores industriais industriais de usinas de energia móvel e de pico, em usinas marítimas e outras instalações industriais onde é necessário o desenvolvimento de grandes capacidades (de 1 a 25 MW) em uma unidade com seu peso e dimensões mínimos.
Um conjunto de requisitos é imposto aos motores de turbina a gás relacionados à confiabilidade, eficiência energética, segurança e respeito ao meio ambiente durante a operação. Juntamente com esses requisitos, os requisitos para a qualidade dos transitórios associados ao lançamento da unidade, uma mudança acentuada na carga selecionada (potência) são relevantes. Em muitos aspectos, a satisfação desses requisitos está no sistema de controle automático (ACS) do motor de turbina a gás.
Um motor de turbina a gás típico usado na indústria é um motor de eixo turbo, cujo circuito é mostrado na Figura 1.
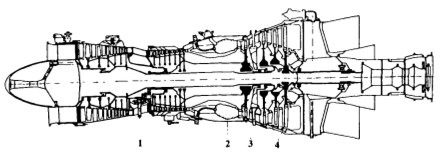
Figura 1. Esquema de um motor de turbina a gás industrial típico:
1- compressor; 2 - uma câmara de combustão; 3 - turbina do compressor; Turbina de 4 potências.
O motor é uma máquina rotativa na qual o ar é comprimido no compressor 1, o combustível fornecido ao ar é queimado na câmara de combustão 2, parte da energia é retirada dos gases quentes na turbina do compressor 3, consumidos pela unidade do compressor 1, 4 gases na turbina elétrica a expansão cria energia retirada do mecanismo pelo consumidor.
Na grande maioria dos motores de turbina a gás, a velocidade do rotor é uma quantidade controlada. Como fator de controle no ACS, a velocidade do rotor n é utilizada no consumo de combustível GT na câmara de combustão. Em diferentes modos de operação e sob várias condições externas, os parâmetros do motor mudam significativamente.
Considere um motor de turbina a gás (GTE) como um objeto de controle instável, para o qual a velocidade do rotor é n variável controlada e o consumo de combustível G T é a ação de controle. Linearizando a dependência do momento da turbina - M T e momento do compressor - M K , na velocidade do rotor e sem levar em consideração a influência da capacidade térmica e de massa do motor para um modo de operação específico, anote a função de transferência do motor da seguinte forma:
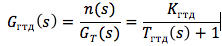
onde o ganho e a constante de tempo são definidos como:
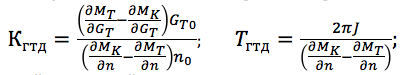
além disso, os sinais de entrada e saída são registrados em desvios adimensionais relativos do estado estacionário (n = Δn / n 0 ; G T = ΔG / G TO , em que os valores básicos dos parâmetros são selecionados para um modo de operação específico do motor, por exemplo, classificado ou máximo). Em diferentes modos de operação e sob várias condições externas, a constante de ganho e tempo do motor muda significativamente, portanto, para cada modo, é necessário determinar seus próprios valores de K GTD e T GTD .
Observe que a função de transferência G do (s) motor (es) de turbina a gás para um objeto de controle instável, como um motor de turbina a gás, é obtida pelo método de coeficientes "congelados" sob a condição de uma mudança bastante lenta nos parâmetros do objeto.
O diagrama de blocos de um sistema eletromecânico analógico para controlar automaticamente a velocidade do rotor de um motor é mostrado na Figura 2
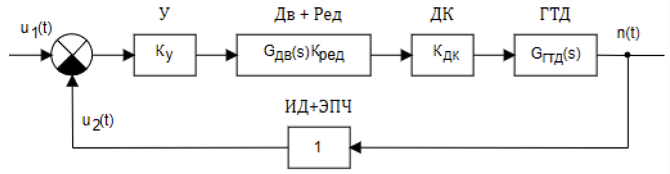
Figura 2. Diagrama de blocos de um SAR GTE analógico
A frequência de rotação é definida pela tensão u 1 (t) e é alterada por um sensor de identificação por pulso, cuja frequência do sinal de saída é determinada pela expressão:
f = kmn, onde n é o número de rotações do motor, m é o número de dentes da engrenagem, k é a relação da engrenagem. A tensão alternada obtida na saída de ID usando o conversor de freqüência eletrônico do EPC é convertida em um sinal u2 (t), cujo valor é proporcional ao número de rotações do motor - n. A tensão u2 (t) é comparada com a tensão de referência e o sinal de erro após o amplificador U ser fornecido ao motor assíncrono bifásico Dv, que regula a válvula de borboleta do DC através da caixa de engrenagens Red, alterando a vazão do combustível que entra no motor da turbina a gás. Um sensor de pulso junto com um conversor de frequência eletrônico pode ser descrito por um link proporcional com uma função de transferência igual à unidade. Nesse caso, o próprio sistema possui um único feedback.
Considerando a conexão serial do amplificador, motor de indução, válvula de borboleta, unidade de turbina a gás e sensor de frequência com um conversor de frequência eletrônico como um objeto de controle comum e usando um controlador fuzzy digital, todo o diagrama de blocos da Figura 2 pode ser reduzido ao diagrama de blocos na Figura 3. Além disso, todos os as funções de transferência dos links são reduzidas a uma função de transferência comum G 0 (s).
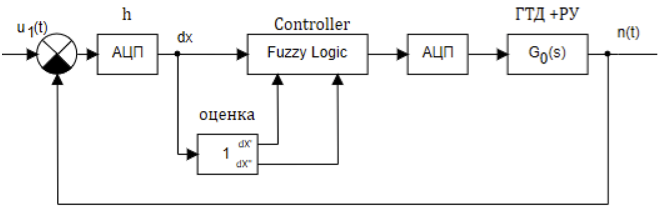
Figura 3. A estrutura do sistema de controle com um controlador difuso.
A função de transferência geral G0 (s) pode ser escrita como:
G 0 (s) = G (s) K EDITAR PARA G (s) = α [s (s + a) (s + b)] -1 , em que
α = ab K Ç K EDIT TO K ,
a = 1 / T DW ,
b = 1 / T GTE
Por exemplo, assumimos que as dependências da função de transferência no tempo de operação assumem os seguintes valores:
T GTD (t) = 0,9849 - 0,1888 × t + 0,0063 × t2 - 0,00012 × t3;
a (t) = 16,5475 - 4,4469 × t + 0,4843 × t2 - 0,02315 × t3 + 0,0004 × t4;
T DW = 0,35 s.
No estudo do sistema de controle, assumimos que a função dada de alterar a velocidade de rotação do rotor de um motor de turbina a gás é definida pela tensão de entrada u (t)
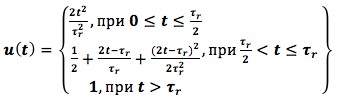
onde τ r é o tempo de aceleração do motor. Tomamos τ r = 6 seg.
Criando um modelo dinâmico
Um modelo simplificado do mecanismo é apresentado na Figura 4. Nesse modelo, usamos parâmetros variáveis de blocos típicos que mudam durante a simulação da dependência fornecida acima.
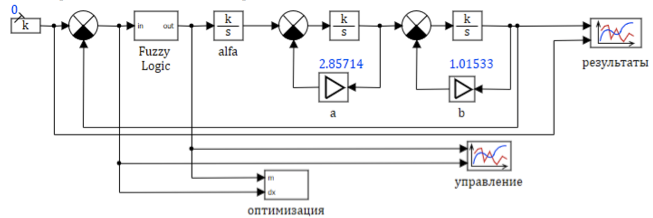
Figura 4. Diagrama estrutural de um modelo de motor de turbina a gás
Os coeficientes dos amplificadores alfa, a, b são calculados usando uma linguagem de script, o texto do programa abaixo:
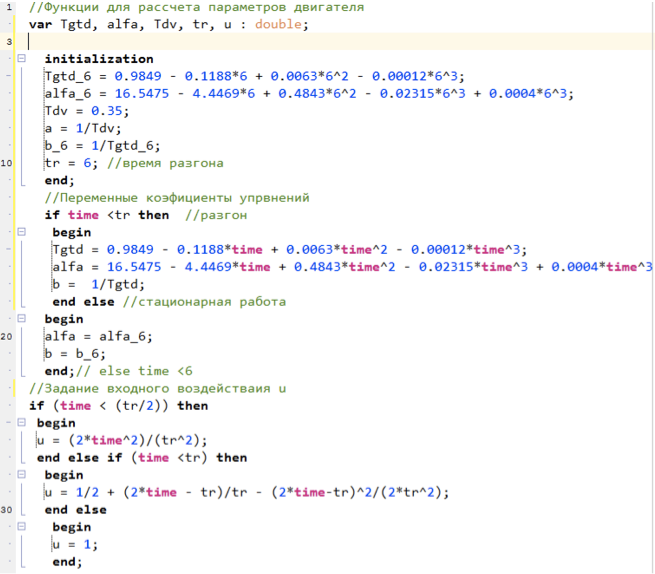
Figura 5. Script para calcular os parâmetros do modelo.
Botão de controle lógico difuso
O regulador de controle faz a entrada da incompatibilidade entre o valor ajustado e o valor obtido no modelo e deve calcular a ação de controle.
Vamos tentar montar um controlador com base na lógica difusa, usando apenas blocos matematicamente padrão de modelagem estrutural, sem usar uma biblioteca especializada.
Uma descrição dos princípios de controle com base na lógica difusa pode ser encontrada no artigo anterior no hub ou na descrição da criação de uma biblioteca especializada de blocos aqui (com cuidado, palavrões).
Qualquer controlador baseado na lógica difusa executa a seguinte sequência de transformações:
- Fase de variáveis de entrada. O valor da variável é substituído por um conjunto de termos.
- Ativação das conclusões das regras da lógica fuzzy.
- Acumulação de conclusões para cada variável linguística.
- Desfazificação de variáveis de saída.
Para controlar o mecanismo, usaremos três variáveis contínuas, que são calculadas com base em um sinal:
- desvio
- desvio derivado (desvio da taxa de variação);
- a segunda derivada do desvio (aceleração das mudanças nos desvios).
O esquema de cálculo é apresentado na Figura 6:
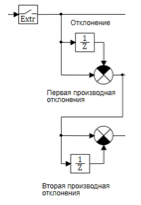
Figura 6. Cálculos do primeiro e do segundo desvio derivado.
O bloco extrapolador quantiza o sinal que entra no controlador com um período de 0,01 seg. As primeira e segunda derivadas são calculadas usando fórmulas de diferença:
 onde:
onde:
u (t) é o desvio atual no tempo t;
u (t-Δt) é o desvio no momento t - Δt;
u '(t) é o valor atual da derivada do desvio no tempo t;
u '(t-Δt) é o valor da derivada do desvio no tempo t - Δt;
u '' (t) é o valor atual da segunda derivada do desvio no tempo t;
u '' (t-Δt) é o valor da segunda derivada do desvio no tempo t - Δt;
Δt é o período de quantização.
A divisão por Δt é realizada na unidade de comparação.
Como resultado desse bloco, três variáveis linguísticas são criadas: desvio, primeira variável de desvio, segunda variável de desvio.
Para resolver o problema do controle difuso, usaremos apenas dois termos para cada variável linguística.
Desvio - menos, mais;
A primeira derivada do desvio está diminuindo, aumentando;
A segunda derivada do desvio - diminui a velocidade, acelera.
Para calcular o valor da função de associação μ para cada termo, usamos uma função linear com saturação. Esta função para o termo é maior que 0 quando o valor de entrada é mínimo e 1 quando o valor de entrada é máximo. Para um termo menor, essa função assume o valor 1 quando a variável é igual ao mínimo e 0 quando a variável é máxima. (ver fig. 7)
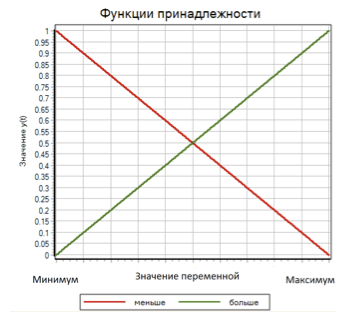
Figura 7. Funções de associação para termos cada vez menos.
Assim, para cada uma das três variáveis de entrada (desvio, a 1ª derivada do desvio, a 2ª derivada do desvio), existem dois termos mais e menos, o valor das funções de associação μ i, que variam linearmente de 0 a 1, dependendo do valor da entrada variável.
Como variável linguística de saída, usamos o efeito de saída, que também possui apenas dois termos para reduzir e aumentar.
A partir do diagrama de modelo da Fig. 4 é óbvio que, se o desvio for menor que 0, o valor será maior que o valor especificado e precisará ser reduzido. Se o desvio for maior que 0, a função será menor que a especificada e precisará ser aumentada.
As regras lógicas para os dois termos terão a seguinte aparência:
- Se menos e diminui e diminui a velocidade => diminui.
- Se mais e aumenta e acelera => aumenta.
Para ativar as regras de inferência difusa, usamos a função mínima para o operador difuso e. O valor das funções de associação para os termos da função de saída é calculado pelas fórmulas:
μ
diminuição = MIN (μ
menor , μ
diminui , μ
diminui )
μ
aumento = MIN (μ
mais , μ
aumenta , μ
acelera )
Para garantir a conversão de termos em valores de impacto específicos (acumulação e desnazificação), usamos o algoritmo Tsukamoto como centro de gravidade dos pontos.
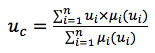 onde
onde
u c é a função resultante;
ui é o valor da função para o termo i;
μ i é o valor da função de associação para termos da função.
No nosso caso, a função resultante para dois termos é calculada pela fórmula:
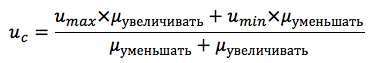
O esquema geral do algoritmo de inferência fuzzy é apresentado na Figura 8:
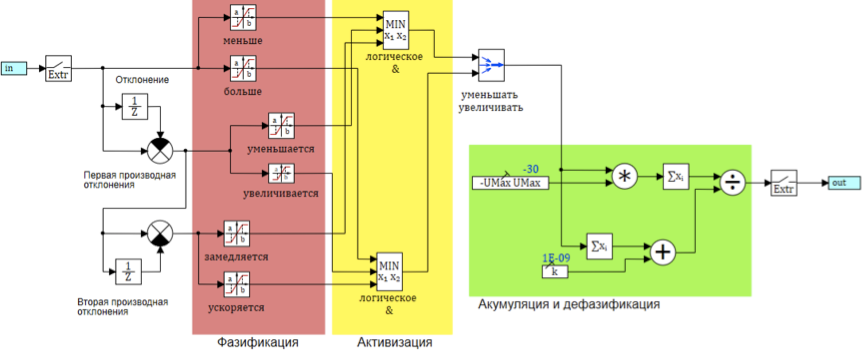
Figura 8. O esquema do algoritmo de inferência fuzzy
Para que esse algoritmo funcione, devemos definir os valores mínimo e máximo para 6 termos de três variáveis linguísticas (desvio, 1ª derivada do desvio, 2ª derivada do desvio). Para reduzir os cálculos, assumimos que o desvio é simétrico em relação a zero. Então é suficiente encontrarmos 3 valores absolutos, um para cada variável.
deltMax - desvio máximo. Define os valores dos termos less, more (-deltMax, deltaMax);
divMax é a derivada máxima do desvio. Define os valores dos termos diminui, aumenta (-divMax, divMax);
div2Max é a segunda derivada máxima. Define os valores dos termos diminui, acelera (-div2Max, div2Max).
O impacto máximo e mínimo de umin e umax são determinados pelos recursos de design e, neste exemplo, são considerados iguais a +30 e -30.
Ajuste do regulador por otimização.
Para selecionar os coeficientes, usamos o mesmo esquema de otimização que usamos em experimentos anteriores com lógica difusa.
Como critério de otimização, assumimos o desvio padrão não superior a 0,001 e o número de comutações na unidade de controle não superior a 25. Para a comutação, alteramos o sinal da ação de controle.
O circuito do bloco de configurações do controlador é mostrado na Fig. 9
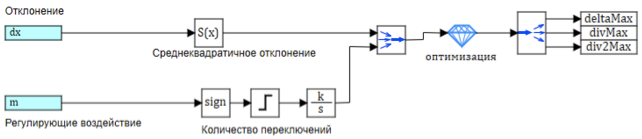
Figura 9. Configurando parâmetros de saída difusa.
Como resultado da operação do bloco, os seguintes parâmetros foram obtidos
deltMax = 0,00746;
divMax = 0,2657;
div2Max = 25,13;
Os resultados da transição são apresentados na Figura 10.
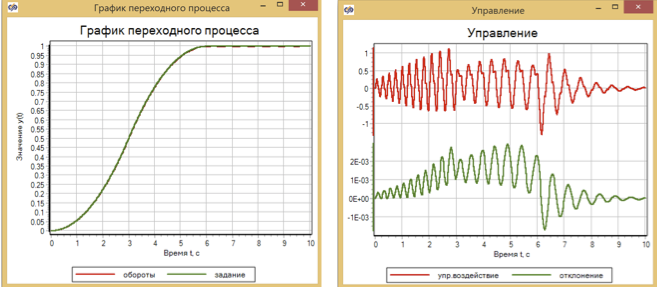
Figura 10. Controle transitório e motor usando lógica fuzzy.
O desvio máximo das revoluções do conjunto após a otimização foi de 2,5 × 10 -3 . O que, em princípio, não é ruim, mas no livro de V.I. Os desvios de convidado no modelo após as configurações eram duas ordens de magnitude menores: o máximo era 5 × 10 -5 .
Para comparação, apresentamos os resultados da operação do controlador PID Fig. 11 e regras de tráfego Fig. 12 para o mesmo modelo de um motor simplificado. Os parâmetros desses reguladores também foram selecionados pelo método de otimização.
Como resultado, é obtido um desvio maior para o controlador PID do que para um controlador baseado na lógica fuzzy - cerca de 6 × 10 -3 , e para um controlador de tráfego que usa a segunda derivada, o desvio é de cerca de 3 × 10 -3 (consulte 13). Além disso, em todos os gráficos, é possível observar que, quando o impacto especificado é alterado (alterações nas seções 3 s e 6 s), a qualidade da regulação muda.
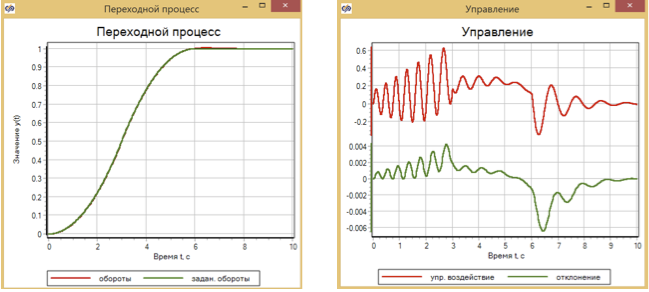
Figura 11. Controle transitório e do motor usando um controlador PID.
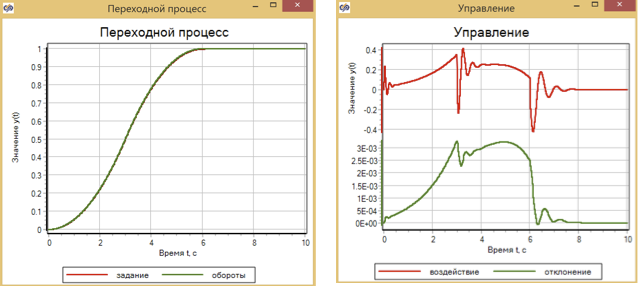
Figura 12. Processo transitório e controle do mecanismo com a ajuda do controlador de tráfego.
Para dar partida no motor, a função de transição é usada na forma de uma mudança suave na velocidade. Também ajustamos os reguladores pelo método de otimização para otimizar o controle de acordo com esta lei. Vamos tentar aplicar um efeito gradual e ver como os reguladores, inicialmente otimizados para um processo de transição suave, podem lidar.
Como efeito, usamos uma etapa de 0 a 1 em 3 segundos do processo.
Os resultados do experimento são apresentados nas figuras 13-15.
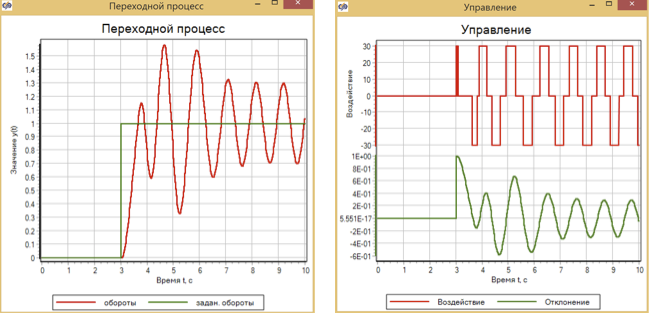
Figura 13. Processo e controle transientes com uma ação de controle gradual com um controlador lógico difuso.
Pode-se observar que um regulador ajustado para uma aceleração suave do motor não lida com o controle durante uma ação gradual, e o sistema entra no modo de oscilação automática.
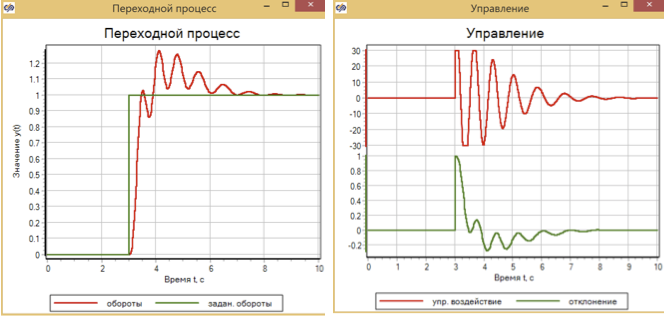
Figura 14. Processo e controle transitório com ação de controle de etapa com controlador PID.
Um controlador PID ajustado para um processo suave, com um efeito gradual, fornece uma transição para um tempo predeterminado, mas, ao mesmo tempo, há uma superação de 30% e um processo oscilatório em 4 segundos.
O controlador de tráfego, configurado para uma regulação suave, com um efeito gradual fornece uma transição suave sem ultrapassagem (Fig. 14)
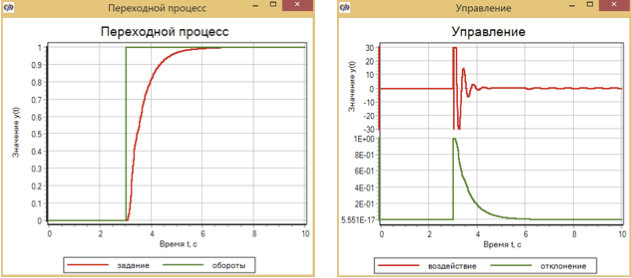
Figura 15. O processo e controle de transição com uma ação de controle escalonada com um controlador de tráfego.
Conclusões
Essas experiências numéricas mostraram que um controlador baseado em lógica nebulosa fornece um controle mais preciso das rotações de um modelo de motor simples, com uma mudança suave no valor definido do que PID e SDA.
No entanto, essa configuração, como se viu, não garante a estabilidade do regulador durante uma ação gradual.
Ao mesmo tempo, para um modelo simplificado do mecanismo, um controlador baseado em lógica nebulosa no caso de uma ação passo a passo mostrou-se pior do que um controlador PID ou SDA.
Link para o arquivo com os projetos do artigo para auto-estudo