Implementação de árvore C de prefixo astuto

1. Introdução

Quatro meses se passaram desde a publicação do artigo sobre minha tentativa de implementação de baixo nível da árvore de prefixos . Apesar de todos os meus esforços, o teto no qual minha implementação anterior da árvore de prefixos acabou sendo capaz era de aproximadamente 80 mil palavras por segundo. Passei muito tempo e energia, mas o resultado seria adequado apenas como um trabalho de laboratório em ciência da computação.

Muitos então me disseram: “Não invente uma bicicleta que já inventamos! Use a solução chave na mão. ” A dificuldade é que eu não poderia usar algo que não entendi, pelo menos em termos gerais.

Acho que entendi a árvore de prefixos, e foi isso que consegui alcançar.

Princípio de funcionamento

Eu não sei muito bem o inglês; portanto, dos muitos artigos que li sobre o tópico prefixos de árvores, algumas das informações provavelmente não chegaram a mim. Portanto, inventei como organizar tudo, entendendo apenas o princípio básico da árvore de prefixos. Para quem não sabe, tentarei descrevê-lo mais claramente do que está escrito na Wikipedia. Então eu expliquei o que estava fazendo com minha esposa.

A árvore de prefixos é uma estrutura lógica para armazenar dados que podem ser representados como um índice de cartão de livros em uma biblioteca. Cada caixa tem um número. Cada caixa corresponde a uma letra específica do alfabeto. No interior estão os números das seguintes gavetas, abertura que você pode descobrir a seguir e assim por diante. Quando não há nada dentro da caixa, isso significa que a letra dessa caixa é a última da palavra. O problema é que algumas caixas permanecem quase vazias, porque contêm 1 ou 2 números e o espaço restante está vazio.

Para resolver esse problema, muitas variedades de árvores de prefixo apareceram, incluindo: HAT-trie, double-array trie, tripple-array trie. Foi precisamente o fato de eu não entender completamente o princípio do trabalho deles que me levou a uma árvore tão simples quanto um arquivo de cartão de biblioteca.

Na última vez, consegui implementar uma implementação de consumo de memória bastante econômica de uma árvore de prefixos simples. Continuando essa metáfora com um arquivo de biblioteca, fiz gavetas de tamanhos diferentes, para o alfabeto completo a caixa é a maior, para uma letra a menor.

Consegui implementar exatamente o mesmo esquema PHP em C.

1. Cada letra da palavra de acordo com a tabela estabelecida é codificada com um número de 2 a 95. Por exemplo, a palavra “abv” é codificada com três números: 11, 12, 13. Para obter o desempenho máximo, uint8_t abc[256][256] = {}; uma matriz bidimensional de números com 1 byte de uint8_t abc[256][256] = {}; Para converter um programa, ele lê uma linha por 1 byte, tenta pegar o valor de cada byte em nossa matriz. Por exemplo, o código do dígito é 1 = 49, então procuramos abc[49][0]; . Se houver um valor diferente de '\ 0', então este é o código da nossa letra, lembre-se e vá para o próximo byte. No nosso caso, a palavra “abv” consiste em uma sequência de 6 bytes, dois bytes por letra: 208, 176, 208, 177, 208, 178. Como a codificação utf-8 foi projetada para que os primeiros bytes de caracteres de byte único nunca coincidam com os primeiros bytes de bytes múltiplos , em nossa matriz abc[208][0] = 0; .

No entanto, para pares de bytes, existem algumas correspondências:

 /*  [11] */ abc[208][176] = 11; /*  [12] */ abc[208][177] = 12; /*  [13] */ abc[208][178] = 13; 

2. Agora precisamos escrever os números 11, 12 e 13 nas caixas da nossa árvore. A árvore consiste em 2 blocos de memória não explosivos separados, o primeiro é um bloco de nós, o segundo é um bloco de links, além de dois contadores de nós ocupados e células ocupadas de um bloco de links. Cada nó da árvore consiste em 16 bytes, 12 bytes de uma máscara de bits e 4 bytes para armazenar o ID do bloco de link. A máscara permite armazenar números de 2 a 96 bits. O primeiro bit da máscara é usado para sinalizar o final da palavra neste nó. Cada nó pode corresponder ao ID do bloco de links se pelo menos 1 letra for escrita nesse nó ou não corresponder se o nó for uma “folha” em termos de árvores, ou seja, uma palavra simplesmente termina nele. Expressa em uma biblioteca, uma gaveta vazia.

3. Pegue a máscara do primeiro nó (raiz). trie-> nós [0] .mask; Contamos os bits gerados nessa máscara, começando do segundo (o primeiro para o sinalizador de fim de palavra). Se não forem levantados bits na máscara, ou seja, Como o nó está vazio, precisamos de um bloco de links de tamanho 1 para armazenar nosso número 11, pegar o número no contador de referência de links do bloco e aumentar o valor antigo em um (porque precisamos do tamanho 1). Pegamos o número no contador do nó e também aumentamos o valor antigo em 1. Escrevemos o ID do bloco de link, que é o número obtido no contador do bloco de link, em nosso nó raiz. E nesse id do bloco de link, escreva o id do novo nó, ou seja, o número obtido no contador do nó. Agora, além do nó raiz (id 0), temos um nó da letra "a" (id 1). Para escrever o número 12 correspondente à letra "b", fazemos o mesmo, mas com o nó da letra "a".

4. Na última letra "c", não precisamos de um lugar no bloco de links, pois teremos o último nó na ramificação ou na folha de nós. Esse nó possui apenas 1 bit na máscara levantada.

5. A parte mais difícil do trabalho de uma árvore ocorre quando é gravada em um nó no qual algumas letras já foram escritas. Nesse caso, o esquema de operação é o seguinte:

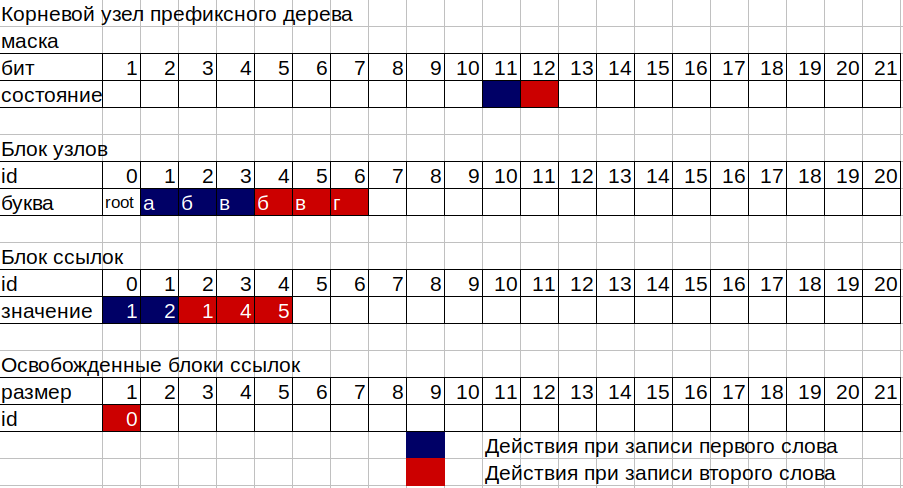
Suponha que desejemos adicionar a palavra "bvg" (12, 13, 14) à nossa árvore, na qual a palavra "abv" (11, 12, 13) já está escrita. Contamos os bits na máscara do nó raiz até o bit da carta de interesse para nós. Temos a letra "b" com o código 12, o que significa que o bit desta letra é 12, na máscara de 1 a 12 bits, o bit 11 da letra "a" já foi aumentado. Portanto, temos o tamanho atual do bloco de links para o nó raiz 1. Escrevemos a segunda letra, agora precisamos de um bloco de links de tamanho 2. Aqui o registro de blocos liberados entra em jogo, no qual o ID e o tamanho das seções no bloco de links não são mais usados ​​pelos nós árvore Nosso antigo ID do bloco de links para o nó raiz do tamanho 1 acaba de entrar no registro de seções livres do tamanho 1, pois nosso nó raiz precisa de um tamanho maior. Nosso registro não possui uma seção adequada do tamanho 2 e, novamente, tomamos o valor do contador do bloco de links como o novo ID do bloco de links, aumentando o contador em 2. No novo endereço do bloco de links na mesma ordem em que os bits da máscara do nó estão localizados, escrevemos o valor do ID nó do antigo bloco de links para a letra "a" da primeira palavra e o valor do nó recém-criado da letra "b" da segunda palavra.

Velocidade de trabalho

O tambor toca ... Lembra do último resultado? Cerca de 80 mil palavras por segundo. A árvore foi criada a partir do dicionário de todas as palavras em russo OpenCorpora 3 039 982 palavras. E aqui está o que aconteceu agora:

 yatrie creation time: 4.588216s (666k wps) yatrie search time 1 mln. rounds: 0.565618s (1.76m wps) 

ATUALIZAÇÃO 11/01/2018:
Na versão 0.0.2, foi possível aumentar a velocidade quase duas vezes, substituindo funções completas por funções macro, além de alterar a estrutura da máscara do nó para uint32_t mask [3], anteriormente era uint8_t mask [12].
Também foram adicionadas macros LIKELY () UNLIKELY () para prever os resultados esperados nos blocos if (), sempre que possível.
ATUALIZAÇÃO 11/05/2018:
Torceu um pouco mais. Consegui fazê-lo funcionar bem, mesmo ao compilar -O3 e -Ofast. A velocidade de pesquisa na árvore é de ~ 0,2 μs ou 0,2c por 1 milhão de repetições. Aparentemente, essa velocidade foi obtida devido à transição para um formato diferente da máscara. Anteriormente, havia 12 bytes de 8 bits e agora 3 int32 e uma função muito rápida para contar bits no int32.

Quão compacto é esse?

O dicionário OpenCorpora especificado ocupa ~ 84MB, o que não é muito pior que libdatrie, que fornece ~ 80MB.

→ Código Fonte

Bem-vindo