Este é um tutorial da biblioteca TensorFlow. Considere um pouco mais profundo do que nos artigos sobre reconhecimento de números manuscritos. Este é um tutorial sobre métodos de otimização. Aqui você não pode prescindir da matemática. Tudo bem se você esqueceu completamente. Lembre-se. Não haverá evidência formal e conclusões complexas, apenas o mínimo necessário para a compreensão intuitiva. Para começar, um pequeno histórico de como esse algoritmo pode ser útil para otimizar uma rede neural.

Seis meses atrás, um amigo me pediu para mostrar como criar uma rede neural em Python. Sua empresa produz instrumentos para medições geofísicas. Várias sondas diferentes durante a perfuração medem um conjunto de sinais associados aos parâmetros do ambiente ao redor do poço. Em alguns casos complexos, calcule com precisão os parâmetros ambientais dos sinais por um longo tempo, mesmo em um computador potente, e é necessário interpretar os resultados das medições em campo. Havia uma idéia de contar centenas de milhares de casos em um cluster e treinar uma rede neural neles. Como a rede neural é muito rápida, ela pode ser usada para determinar parâmetros consistentes com os sinais medidos, exatamente no processo de perfuração. Os detalhes estão no artigo:
Kushnir, D., Velker, N., Bondarenko, A., Dyatlov, G., & Dashevsky, Y. (2018, 29 de outubro). Simulação em tempo real da ferramenta de resistividade azimutal profunda no modelo de falhas 2D usando redes neurais (russo). Sociedade de Engenheiros de Petróleo. doi: 10.2118 / 192573-RU
Uma noite, mostrei como as keras poderiam implementar uma rede neural simples, e um amigo no trabalho começou a treinar nos dados contados. Depois de alguns dias, discutimos o resultado. Do meu ponto de vista, ele parecia promissor, mas um amigo disse que precisava de cálculos com a precisão do dispositivo. E se o erro quadrático médio fosse em torno de 1, seria necessário 1e-3. 3 pedidos menos. Mil vezes.
Experimentos com arquitetura de rede neural, normalização de dados e abordagens de otimização renderam quase nada. Depois de algumas semanas, um amigo ligou e disse que instalou o MatLab e resolveu o problema pelo método Levenberg-Marquardt (a seguir, chamaremos LM ). Foi otimizado por um longo tempo (vários dias), não funcionou na GPU, mas o resultado foi o correto. Pareceu um desafio.
A pesquisa rápida de um otimizador LM pronto para keras ou TensorFlow falhou. Encontrei apenas a biblioteca pyrenn, mas sua funcionalidade me pareceu fraca. Eu decidi implementá-lo eu mesmo. À primeira vista, tudo parecia simples, e duas noites deveriam ter sido suficientes. Demorou mais tempo. Havia dois problemas:
- TensorFlow. Um monte de artigos, mas quase todos os níveis ", mas vamos escrever um
olá mundo reconhecimento de dígitos manuscritos". - Matemática Eu esqueci muito, e os autores de artigos matemáticos não se importam com pessoas como eu: fórmulas sólidas sem explicação, “obviamente!” e assim por diante.
Como resultado, ele escreveu um artigo para aqueles que esqueceram a matemática e querem entender o TensorFlow um pouco mais fundo, mas sem hardcore. O artigo tem muito texto e pouco código. A opção oposta, quando há pouco texto e muito código, é aqui o Jupyter Notebook Levenberg-Marquardt .
Conheça o recurso Rosenbrock
Geraremos dados de treinamento pela função Rosenbrock , que geralmente é usada como referência para algoritmos de otimização:
f ( x , y ) = ( a - x ) 2 + b ( y - x 2 ) 2
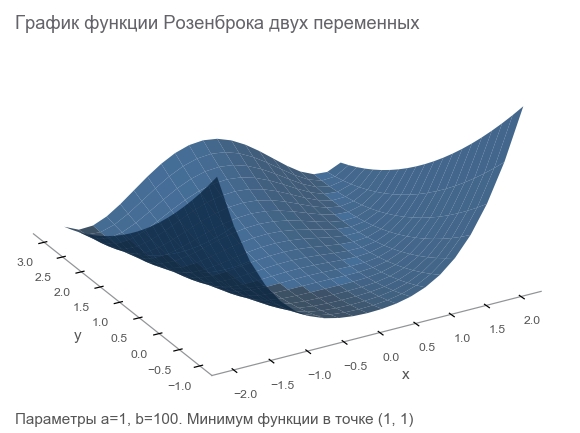
Por que ela é boa?
- Horário bonito. É chamado Vale de Rosenbrock e a função banana intraduzível de Rosenbrock .
- O mínimo global está dentro de um vale longo, estreito e parabólico. Encontrar um vale é trivial e um mínimo global é difícil.
- Existe uma opção multidimensional. Não é tão fácil criar uma boa função para muitas variáveis.
Começaremos a escrever o código dele, conectando as bibliotecas necessárias para mais trabalhos:
import numpy as np import tensorflow as tf import math def rosenbrock(x, y, a, b): return (a - x)**2 + b*(y - x**2)**2
Afirmamos o problema
Como estávamos falando de um dispositivo de medição, vamos continuar usando a analogia. Nosso dispositivo em um mundo fictício pode medir coordenadas ( x , y ) e altura z . Os físicos estudaram o mundo e disseram: " Sim, é Rosenbrock! Conhecendo as coordenadas, você pode calcular com precisão a altura, não é necessário medi-la ". Em outras palavras, os cientistas nos deram um modelo z = r o s e n b r o c k ( x , y , a , b ) que depende dos parâmetros ( a , b ) . Esses parâmetros, embora constantes em um mundo fictício, são desconhecidos. Eles precisam ser encontrados.
Realizamos uma série de experimentos que deram m pontos (x1,y1,z1),(x2,y2,z2),...,(xm,ym,zm) :
A primeira maneira de otimizar é tentar adivinhar os parâmetros. Usamos a biblioteca Numpy:
x, y = data_points[:, 0], data_points[:, 1] z = data_points[:, 2]
Como entender como estamos errados? Contagem de resíduos - tamanhos de erro. m pontos dão m resíduos - você precisa de um indicador integral. Nós quadrado cada resíduo em um quadrado e calculamos a média:
MSE(a,b)= frac1m summi=1(zi− widehatzi)2
Essa medida de proximidade é chamada de erro médio quadrático (a seguir denominado mse ):
[Out]: 3868.2291666666665
Ao minimizar o mse , resolvemos o problema dos mínimos quadrados ( minimização de quadrados não lineares ):
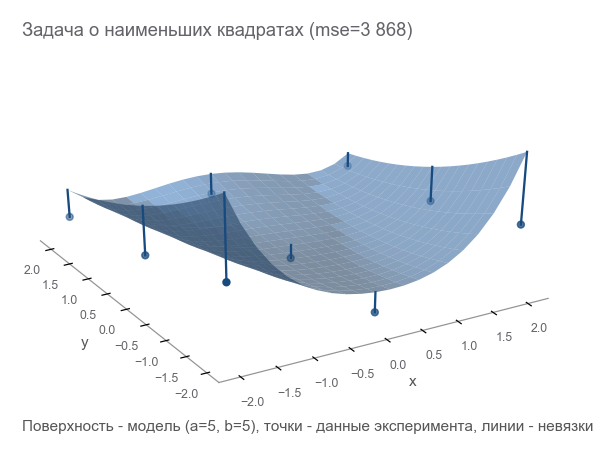
Pode-se ver que os parâmetros não foram adivinhados.
Formulamos o problema no TensorFlow
O modelo tem a forma z=rosenbrock(x,y,a,b) . Trazemos para o formulário y=f(x,p) (geralmente matemática escreve beta em vez de p mas os programadores não usam beta). Agora o modelo tem a forma y=rosenbrock(x,p) onde y - altura x É o vetor de coordenadas de dois elementos (componente) e p - vetor de parâmetros.
Os programadores costumam pensar em vetores como matrizes unidimensionais. Isso não está totalmente correto. Uma matriz de números é um meio de representar um vetor. Você pode representar um vetor como uma matriz de dimensão N matriz bidimensional 1 vezesN e até uma matriz N vezes1 nos casos em que o fato de o vetor ser um vetor de coluna (por exemplo, multiplicar uma matriz por ele) é importante:
beginbmatrixx1 vdotsxN endbmatrix
O TensorFlow usa o conceito de tensor . Um tensor , como uma matriz, pode ser unidimensional (para representar um vetor ), bidimensional (para um vetor de matriz ou coluna ) e qualquer dimensão maior.
O código TensorFlow não é diferente no código Numpy. O conteúdo é enorme. O código numpy calcula o valor mse. O código TensorFlow não realiza nenhum cálculo, forma um gráfico de fluxo de dados que mse pode calcular . Um momento muito tolerante ao cérebro é o trabalho da função rosenbrock . Usamos nos dois casos. Mas quando passamos as matrizes Numpy, ele executa os cálculos pela fórmula e retorna os números. E quando transferimos os tensores para o TensorFlow, ele forma um subgráfico do fluxo de dados e retorna sua borda na forma de um tensor. Milagres de polimorfismo, mas não os abuse:
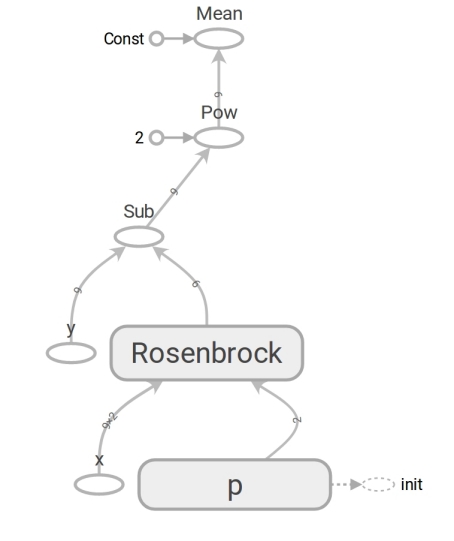
Graças à presença de um gráfico de fluxo de dados, o TensorFlow, em particular, pode calcular derivadas automaticamente (usando a técnica de diferenciação automática no modo reverso ).
Um momento de matemática. Blocos "para quem esqueceu" serão escondidos em um spoiler.
Derivada (número digitado - número restante)Muito provavelmente você se lembra da definição da derivada de uma função escalar (retornando um número) de uma variável: para f: mathbbR rightarrow mathbbR derivado f no ponto x in mathbbR definido como:
f′(x)= limh to0 fracf(x+h)−f(x)h$
Derivados são uma maneira de medir mudanças . No caso escalar, a derivada mostra quanto a função mudará f se x mude para um valor pequeno varepsilon :
f(x+ varepsilon) aproxf(x)+ varepsilonf′(x)
Por conveniência, denotamos y=f(x) e o derivado y por x vamos escrever como frac parcialy parcialx . Esse registro enfatiza que frac parcialy parcialx - taxa de variação entre variáveis x e y . Mais especificamente, se x mude para varepsilon então y mude para aproximadamente varepsilon frac parcialy parcialx . Você também pode escrever assim:
x rightarrowx+ Deltax rightarrow rightarrow aproximadamentey+ frac parcialy parcialx Deltax
Lê como: "mudando x em x+ Deltax mudar y aproximadamente y+ Deltax frac parcialy parcialx ". Esse registro destaca claramente o vínculo entre a mudança x e mudar y .
Construímos um gráfico de fluxo de dados, vamos executar o cálculo do mse:
[Out]: 3868.2291666666665
O resultado é o mesmo que com o Numpy. Então eles não estavam enganados.
Comece a otimizar
Infelizmente, não foi possível adivinhar os parâmetros. Mas então nós:
- Definimos o critério de otimização - o valor mínimo de mse.
- Os parâmetros variáveis foram determinados: vetor p com componentes a , b Funções Rosenbrock.
- Ainda não pensamos em limitações, mas elas não estão lá.
Na última etapa, construímos um gráfico de fluxo de dados com um tensor de perda finita ( função de perda ). O objetivo da otimização é encontrar o valor do vetor de parâmetros p em que o valor da função de perda é mínimo. Tivemos sorte, o gráfico desta função é muito simples (côncavo e sem mínimos locais):
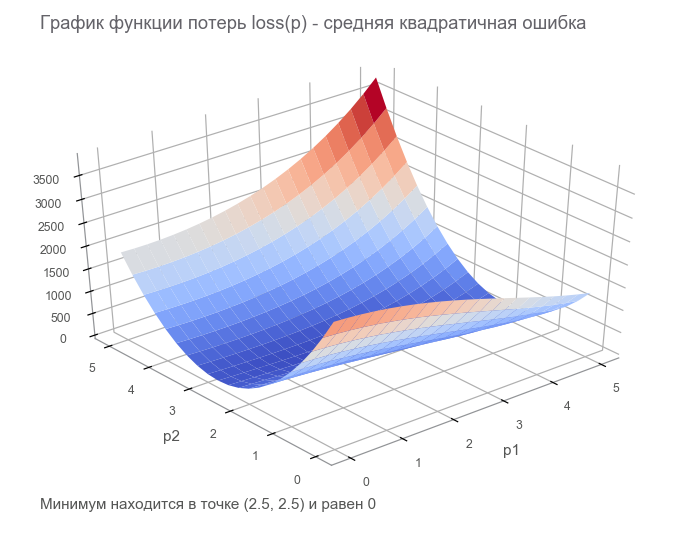
Introdução à otimização. Para começar, escrevemos um ciclo generalizado:
Otimizamos pelo método da descida de gradiente mais rápida (SGD)
As ações desse método podem ser comparadas ao montar um esquiador ousado, que sempre desce a ladeira (na direção mais íngreme). Nesse caso, apenas a inclinação no ponto de localização é levada em consideração. E se a inclinação for forte, o esquiador voa uma longa distância antes da próxima mudança. Com uma inclinação fraca, ele se move em pequenos passos. Talvez como voar para longe em uma árvore (o algoritmo diverge ) e fica preso em um poço ( mínimo local ).

Você pode escrever da seguinte forma (alterar boldsymbolp em boldsymbolp−... ):
boldsymbolp rightarrow boldsymbolp− alpha[ nablapperda( boldsymbolp)]
Gorduroso boldsymbolp enfatiza que este é o ponto da localização real - o valor do vetor de parâmetro na etapa atual. No primeiro passo, esse é o nosso palpite (5, 5). Existem dois pontos interessantes na fórmula: alpha - taxa de aprendizagem ( taxa de aprendizagem ), nablapperda - gradiente ( gradiente ) da função de perda pelo vetor de parâmetros.
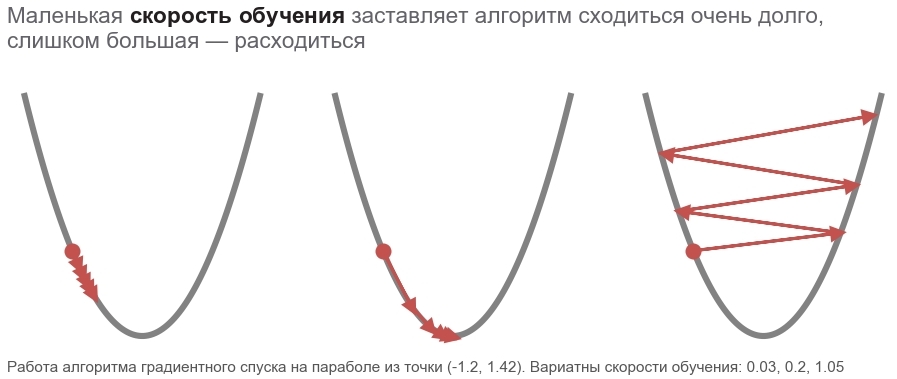
Gradiente (vetor inserido - número restante)Considere uma função que recebe um vetor como entrada e produz um escalar: f: mathbbRN rightarrow mathbbR . Derivada f no ponto x in mathbbRN agora chamado de gradiente e é um vetor [ nablaxf(x)] in mathbbRN (lido como "nabla") composto por derivadas parciais :
nablaxy=( frac parcialy parcialx1, frac parcialy parcialx2,..., frac parcialy parcialxN)
Nesse caso, o registro da dependência da alteração da função na alteração do argumento tem a seguinte forma:
x rightarrowx+ Deltax rightarrow rightarrow aproximadamentey+ nablaxy cdot Deltax
O registro mudou bastante para levar em conta que x , Deltax e nablaxy - vetores em mathbbRN e y - escalar. Ao multiplicar vetores nablaxy e Deltax o produto escalar é usado (a soma dos produtos dos componentes).
[Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 1381.5379689135807 [...] ENDED ON STEP: 582, FINAL LOSS: 9.698531012270816e-11 PARAMETERS: [2.50000205 2.49999959]
Foram necessárias 582 etapas:
Movimento na direção do anti-gradientePor que estamos nos movendo na direção oposta ao gradiente? Lembre-se da entrada com o produto escalar: x rightarrowx+ Deltax rightarrow rightarrow aproximadamentey+ nablaxy cdot Deltax . Minimizar y . Como o comportamento da função é conhecido apenas em uma vizinhança pequena por meio da derivada, é necessário avançar em etapas pequenas, porém ótimas, minimizando o produto nablaxy cdot Deltax . Por definição de escola, o produto escalar de dois vetores é o número igual ao produto dos comprimentos desses vetores pelo cosseno do ângulo entre eles : a cdotb= esquerda|a direita| esquerda|b direita|cos ângulo(a,b) . Para um comprimento fixo de vetores, este produto atinge um mínimo com um cosseno de -1, ou seja, em um ângulo de 180 graus, quando os vetores são direcionados em direções opostas. Consequentemente, o produto escalar mínimo nablaxy cdot Deltax alcançado quando Deltax na direção do anti-gradiente .
Otimizamos pelo método Adam
Não vamos avançar nos métodos de gradiente, mas há muitas variações. Você pode ler sobre eles no artigo Métodos de otimização de redes neurais . No TensorFlow, muitos otimizadores já estão implementados. Por exemplo, Adam:
[Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 34205.72916492336 [...] ENDED ON STEP: 317, FINAL LOSS: 2.424142714263483e-12 PARAMETERS: [2.49999969 2.50000008]
Gerenciado em 317 etapas. Muito mais rapido
Otimizamos pelo método de Newton
As ações dos métodos de segunda ordem podem ser comparadas à pilotagem de um snowboardista de freeride racional que pondera o próximo ponto de sua rota por um longo tempo e leva em consideração não apenas a inclinação do local, mas também a curvatura.
De fato, os métodos de descida de gradiente e os de segunda ordem tentam adivinhar ( aproximar ) a função no ponto atual. Os métodos de gradiente focam apenas a inclinação do gráfico da função no ponto - a primeira derivada. Os métodos de segunda ordem, além do viés, levam em consideração a curvatura , a segunda derivada: "se a curvatura persistir, onde será o mínimo?" Nós calculamos e vamos lá:
Para construir essa aproximação e calcular o ponto mínimo estimado, você pode usar a série de Taylor . Para o caso unidimensional, a aproximação por um polinômio de segunda ordem no ponto a é assim:
f(x) approxf(a)+ fracf′(a)(x−a)1!+ fracf″(a)(x−a)22!
O mínimo é atingido em x=a− fracf′(a)f″(a) . O caso multidimensional parece mais sério:
Matriz Hessiana (vetor inserido - número à esquerda)A matriz hessiana é uma matriz quadrada composta de segundas derivadas:
\ boldsymbol {H} y_ {x} = \ begin {bmatrix} \ frac {\ parcialmente ^ 2y} {\ parcial x_1 ^ 2} & \ frac {\ parcial ^ 2y} {\ parcial x_1 \ parcial x_2} & \ cdots e \ frac {\ parcial ^ 2y} {\ parcial x_1 \ parcial x_N} \\ \ frac {\ parcial ^ 2y} {\ parcial x_2 \ parcial x_1} & \ frac {\ parcial ^ 2y} {\ parcial x_2 ^ 2} & \ cdots & \ frac {\ parcial ^ 2y} {\ parcial x_2 \ parcial x_N} \\ \ vdots e \ vdots e \ ddots e \ vdots \\ \ frac {\ parcial ^ 2y} {\ parcial x_N \ parcial x_1} & \ frac {\ parcial ^ 2y} {\ parcial x_N \ parcial x_2} & \ cdots & \ frac {\ parcial ^ 2y} {\ parcial x_N ^ 2} \ end {bmatrix}
Aproximação de um polinômio de segunda ordem para uma função de um vetor por meio de um gradiente e uma matriz Hessiana em um ponto a é assim:
f(x) aproximadamentef(a)+(xa) intercal[ nablaxf(a)]+ frac12!(xa) intercal[ boldsymbolHfx(a)](xa)
O mínimo é atingido em x=a−[ boldsymbolHfx(a)]−1[ nablaxf(a)] . A forma praticamente coincide com o caso unidimensional: substituímos a primeira derivada por um gradiente, a segunda por uma matriz Hessiana e fizemos uma correção para trabalhar com vetores. É impossível dividir um vetor por uma matriz, portanto, a multiplicação pela matriz inversa é usada. T significa transpor . A fórmula implica que, por padrão, um vetor é uma coluna. Transpose transforma um vetor de coluna em um vetor de linha . Ao implementar no TensorFlow, isso deve ser levado em consideração, mas na direção oposta: por padrão, o vetor é uma sequência (tensor unidimensional). Apenas no caso: a transposição não é uma rotação de 90 graus, é a transformação de linhas em colunas na mesma ordem.
Portanto, a etapa do método Newton tem a seguinte forma:
boldsymbolp rightarrow boldsymbolp−[ boldsymbolHlossp( boldsymbolp)]−1[ nablapperda( boldsymbolp)]
O TensorFlow tem tudo para implementar este método:
[Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 105.04357496954218 step: 4, current loss: 9.96663526704236 ENDED ON STEP: 6, FINAL LOSS: 5.882202372519996e-20 PARAMETERS: [2.5 2.5]
Bastante 6 etapas:
Otimizado pelo algoritmo de Gauss-Newton
O método de Newton tem uma desvantagem - a matriz hessiana. Graças ao TensorFlow, podemos contá-lo em uma linha de código. Segundo o wiki, Johann Karl Friedrich Gauss fez a primeira menção de seu método em 1809. O cálculo da matriz de Hessian para vários parâmetros para o método dos mínimos quadrados pode levar muito tempo. Agora podemos assumir que o algoritmo de Gauss-Newton usa a aproximação da matriz de Hessian através da matriz de Jacobi para simplificar os cálculos. Mas, do ponto de vista da história, não é assim: Ludwig Otto Hesse (que desenvolveu a matriz com o nome dele) nasceu em 1811 - 2 anos após a primeira menção do algoritmo. E Carl Gustav Jacobi tinha 5 anos.
O algoritmo de Gauss-Newton não funciona com a função de perda. Funciona com a função residual r(p) . Esta função aceita um vetor de entrada de parâmetros p e retorna um vetor de resíduos . No nosso caso, o vetor p consiste em 2 componentes (parâmetros a e b Funções de Rosenbrock) e o vetor residual de m componente (de acordo com o número de experiências). A função vetorial do argumento vetorial é obtida. Sua derivada:
Matriz Jacobi (vetor inserido - vetor liberado)Considere uma função que recebe um vetor como entrada e também produz um vetor: f: mathbbRN rightarrow mathbbRM . Derivada f no ponto x agora tem tamanho N vezesM , chamada matriz de Jacobi , e consiste em todas as combinações de derivadas parciais:
\ boldsymbol {J} y_ {x} = \ begin {pmatrix} \ frac {\ parcial y_ {1}} {\ parcial x_ {1}} & \ cdots & \ frac {\ parcial y_ {1}} {\ x_ parcial {N}} \\ \ vdots e \ pontos e \ vdots \\ \ frac {\ parcial y_ {M}} {\ parcial x_ {1}} & \ cdots & \ frac {\ parcial y_ {M}} {\ parcial x_ {N}} \ end {pmatrix}
Você pode perceber que as linhas da matriz Jacobi são os gradientes dos componentes y . Item (i,j) matrizes frac parcialy parcialx é igual a frac parcialyi parcialxj e nos diz quanto vai mudar yi quando mudar xj em um pequeno valor. Como nos casos anteriores, você pode escrever:
x rightarrowx+ Deltax rightarrow rightarrow aproximadamentey+ boldsymbolJyx Deltax
Aqui boldsymbolJyx matriz N vezesM e Deltax tamanho do vetor N assim o produto boldsymbolJyx Deltax É o produto da matriz pelo vetor, resultando em um vetor de tamanho M .
Para não nos confundirmos com a abundância de caracteres, assumimos que boldsymbolJr - matriz de Jacobi de funções residuais no ponto atual boldsymbolp . Então o algoritmo de Gauss-Newton pode ser escrito da seguinte maneira:
boldsymbolp rightarrow boldsymbolp−[ boldsymbolJ rintercal boldsymbolJr]−1 boldsymbolJ rintercalr( boldsymbolp)
A gravação na forma coincide completamente com a gravação do método de Newton. Somente em vez da matriz Hessiana é usada boldsymbolJ rintercal boldsymbolJr em vez do gradiente boldsymbolJ rintercalr( boldsymbolp) . A seguir, veremos por que essa aproximação pode ser usada. Enquanto isso, vamos prosseguir com a implementação no TensorFlow:
[Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 14.653025157673625 step: 4, current loss: 4.3918079172783016e-07 ENDED ON STEP: 4, FINAL LOSS: 3.374364957618591e-17 PARAMETERS: [2.5 2.5]
Suficiente 4 etapas. Menor que para o método de Newton.
Como pode ser visto no código, a função de perda não é usada na otimização, apenas nos critérios de parada e registro. Como o algoritmo de otimização sabe qual função minimizar? A resposta é surpreendente: de jeito nenhum! Gauss-Newton minimiza apenas o erro quadrático médio .
Corrija a parte matemática do artigo
Repetimos toda a matemática que precisávamos. Vamos corrigi-lo um pouco para focar ainda mais a programação e o TensorFlow. Você pode precisar de um lápis para rastrear a sequência de ações matemáticas.
Existe um modelo y=f(x,p) onde x - vetor p - vetor de parâmetros de dimensão n e y - escalar. Das experiências recebidas m pontos (x1,y1),...,(xm,ym) ( pares de dados ). A função residual do vetor depende apenas do vetor de parâmetro: r(p)=(r1(p),...rm(p)) onde rk(p)=yk− widehatyk=yk−f(xk,p) . , p , xk,yk ? , xk,yk , .
p , ( sum of squared error — sse residual sum-of-squares — rss ) . mse sse , m . . :
loss(p)=r21(p)+⋯+r2m(p)=m∑k=1r2k(p)
p (p) .
, . — . — , r2 2r∂r∂p . :
∇ploss=(m∑k=12rk∂rk∂p1,⋯,m∑k=12rk∂rk∂pn)
. :
[Hlossp]ij=∂2loss∂pi∂pj=m∑k=1(2∂rk∂pi∂rk∂pj+2rk∂2rk∂pi∂pj)
. , , (uv)′=u′v+uv′ .
Ótimo! .
, , , — 2rk∂2rk∂pi∂pj . , , rk , . — . , ? -.
:
Jr=(∂r1∂p1⋯∂r1∂pn⋮⋱⋮∂rm∂p1⋯∂pm∂pn)
, , . Note que:
2Jr⊺
"" . ( ). , — , .
( ):
, , - — , mse .
. , , . , . , .
, : " . - ! ". , , , ( supervised learning ). , . : ( training set ) — ; — ( prediction model ) ; — , .
( multi-layer perceptron neural network mlp ). , , :
- ( starting values ) . Xavier'a, .
- ( overfitting ). — . , . — .
- ( scaling of the input ). , .
9 . 500:
500 . — ( learner ), ( outcome measurement ) ( features ) .
( network diagram ). MatLab:
( input ). ( weights ) 2x10, ( bias ) 10, ( activation ). () ( hidden layer ) 10 . , , ( output ).
, , ( ):
:
. "" , - . 41 . , .
, . - de :
Adam
Adam . mse :
[Out]: step: 1, current loss: 671.4242576535694 [...] ENDED ON STEP: 40000, FINAL LOSS: 0.22862158574440725 VALIDATION LOSS: 0.29000289644978866
. : , , .
2 . :
:
. , 4 . 4 tf.concat .
. tf.while_loop , , , stack .
: . tf.reshape (-1,) .
. - . — TensorFlow . — - - . -. Levenberg-Marquardt Jupyter Notebook rosenbrock_train.py . , TensorFlow . - , ( ) , , .
-
hess_approx grad_approx -. , . :
- :
- :
, , , . - , :
, - .
[Out]: step: 1, current loss: 548.8468777701685 step: 2, current loss: 49648941.340197295 InvalidArgumentError: Input is not invertible.
- . , . - , .
, .
-
. Matlab trainlm . . MathWorks.
- : . - :
( ). , -. , . , LM -.
:
mu = tf.placeholder(tf.float64, shape=[1]) n = tf.add_n(parms_sizes) I = tf.eye(n, dtype=tf.float64)
? LM - . , . , , . — , mse . , :
[Out]: step: 1, mu: 3.0 current loss: 692.6211687622557 [...] ENDED ON STEP: 100, FINAL LOSS: 0.012346989371823602 VALIDATION LOSS: 0.01859463694102034
100 LM mse 10 , 40 .
. , . , rosenbrock_train.py .
2D . . . , " " ( curse of dimentionality , Bellman, 1961). . .
:
rosenbrock_train.py get_rand_rosenbrock_points .
-
- : " ! 4 , 300! ". , ( ) -. , , . - . . : ? , . . , - :
- 10 000 6D .
- 3 12, 10, 8 (311 ).
- .
- 3.5 .
. - 2 . LM . 20 .
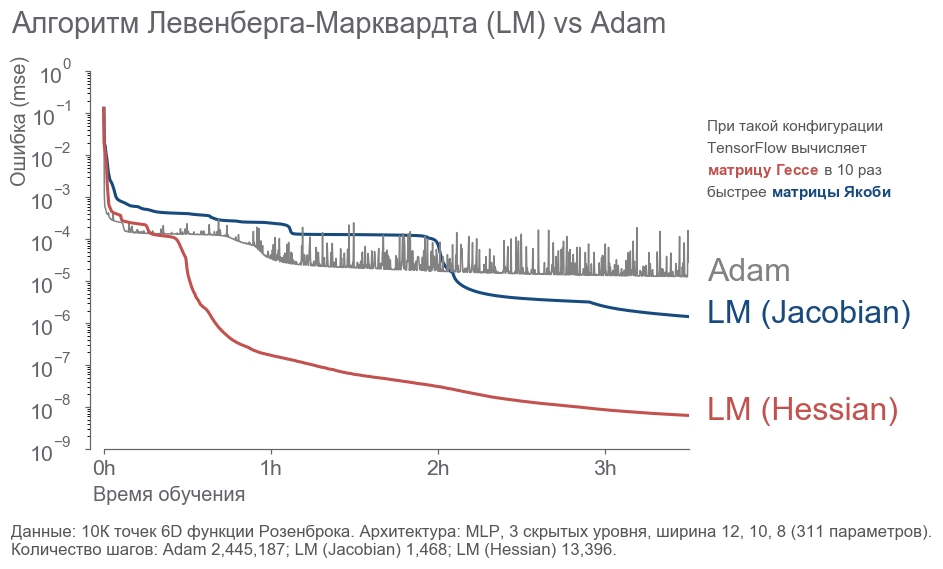
rosenbrock_train.py . . , .
Conclusão
, . " ", , . , . , 273 . - , .
, :
- .
- ( ) -:
[1] Petros Drineas, Ravi Kannan, and Michael W. Mahoney. 2006. Fast Monte Carlo Algorithms for Matrices I: Approximating Matrix Multiplication. SIAM J. Comput. 36, 1 (July 2006), 132-157. DOI= http://dx.doi.org/10.1137/S0097539704442684
[2] Adelman, M., & Silberstein, M. (2018). Faster Neural Network Training with Approximate Tensor Operations. CoRR, abs/1805.08079.
, - . , . "".