Aproximamos a função usando uma rede neural

Para desenvolver bibliotecas para trabalhar com redes neurais, resolveremos o problema de aproximar a função de um único argumento usando algoritmos de redes neurais para treinamento e previsão.

Entrada

Seja dada uma função f: [x0, x1] -> R

Nós aproximamos a função dada f pela fórmula

P(x) = SUM W[i]*E(x,M[i]) 

onde

• i = 1..n
• M [i] de R
• W [i] de R
• E (x, M) = {0, para x <M; 1/2, com x = M; 1, para x> M

Obviamente, com uma distribuição uniforme dos valores de M [i] no intervalo (x0, x1), existem valores de W [i] tais que a fórmula P (x) se aproxima melhor da função f (x). Além disso, para determinados valores de M [i] definidos no intervalo (x0, x1) e ordenados em ordem crescente, podemos descrever um algoritmo seqüencial para calcular as quantidades W [i] para a fórmula P (x).

E aqui está a rede neural

Transformamos a fórmula P (x) = SUM W [i] * E (x, M [i]) em um modelo de rede neural com um neurônio de entrada, um neurônio de saída ne neurônios de camada oculta

 P(x) = SUM W[i]*S(K[i]*x + B[i]) + C 

onde

• variável x - camada "entrada" composta por um neurônio
• {K, B} - parâmetros da camada "oculta", composta por n neurônios e função de ativação - sigmoide
• {W, C} - parâmetros da camada "output", consistindo em um neurônio, que calcula a soma ponderada de suas entradas.
• S é um sigmóide,

enquanto

• parâmetros iniciais da camada "oculta" K [i] = 1
• os parâmetros iniciais da camada "oculta" B [i] são distribuídos igualmente no segmento (-x1, -x0)

Todos os parâmetros da rede neural K, B, W e C são determinados pelo treinamento da rede neural nas amostras (x, y) dos valores da função f.

Sigmoid

Sigmoide é uma função não-linear crescente monotônica suave

• S (x) = 1 / (1 + exp (-x)).

O programa

Usamos o pacote Tensorflow para descrever nossa rede neural.

 #        x = tf.placeholder(tf.float32, [None, 1], name="x") #        y = tf.placeholder(tf.float32, [None, 1], name="y") #   nn = tf.layers.dense(x, hiddenSize, activation=tf.nn.sigmoid, kernel_initializer=tf.initializers.ones(), bias_initializer=tf.initializers.random_uniform(minval=-x1, maxval=-x0), name="hidden") #   model = tf.layers.dense(nn, 1, activation=None, name="output") #    cost = tf.losses.mean_squared_error(y, model) train = tf.train.GradientDescentOptimizer(learn_rate).minimize(cost) 

Treinamento

 init = tf.initializers.global_variables() with tf.Session() as session: session.run(init) for _ in range(iterations): train_dataset, train_values = generate_test_values() session.run(train, feed_dict={ x: train_dataset, y: train_values }) 

Texto completo

 import math import numpy as np import tensorflow as tf import matplotlib.pyplot as plt x0, x1 = 10, 20 #    test_data_size = 2000 #      iterations = 20000 #    learn_rate = 0.01 #   hiddenSize = 10 #    #     def generate_test_values(): train_x = [] train_y = [] for _ in range(test_data_size): x = x0+(x1-x0)*np.random.rand() y = math.sin(x) #   train_x.append([x]) train_y.append([y]) return np.array(train_x), np.array(train_y) #        x = tf.placeholder(tf.float32, [None, 1], name="x") #        y = tf.placeholder(tf.float32, [None, 1], name="y") #   nn = tf.layers.dense(x, hiddenSize, activation=tf.nn.sigmoid, kernel_initializer=tf.initializers.ones(), bias_initializer=tf.initializers.random_uniform(minval=-x1, maxval=-x0), name="hidden") #   model = tf.layers.dense(nn, 1, activation=None, name="output") #    cost = tf.losses.mean_squared_error(y, model) train = tf.train.GradientDescentOptimizer(learn_rate).minimize(cost) init = tf.initializers.global_variables() with tf.Session() as session: session.run(init) for _ in range(iterations): train_dataset, train_values = generate_test_values() session.run(train, feed_dict={ x: train_dataset, y: train_values }) if(_ % 1000 == 999): print("cost = {}".format(session.run(cost, feed_dict={ x: train_dataset, y: train_values }))) train_dataset, train_values = generate_test_values() train_values1 = session.run(model, feed_dict={ x: train_dataset, }) plt.plot(train_dataset, train_values, "bo", train_dataset, train_values1, "ro") plt.show() with tf.variable_scope("hidden", reuse=True): w = tf.get_variable("kernel") b = tf.get_variable("bias") print("hidden:") print("kernel=", w.eval()) print("bias = ", b.eval()) with tf.variable_scope("output", reuse=True): w = tf.get_variable("kernel") b = tf.get_variable("bias") print("output:") print("kernel=", w.eval()) print("bias = ", b.eval()) 

Foi o que aconteceu

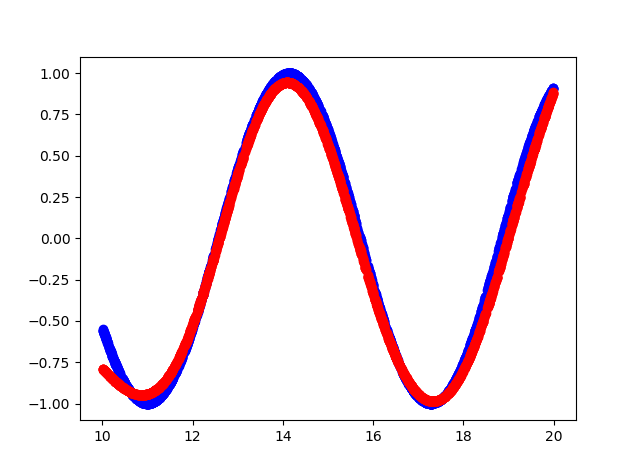
• Azul é a função original.
• Cor vermelha - aproximação da função

Saída do console

 cost = 0.15786637365818024 cost = 0.10963975638151169 cost = 0.08536215126514435 cost = 0.06145831197500229 cost = 0.04406769573688507 cost = 0.03488277271389961 cost = 0.026663536205887794 cost = 0.021445846185088158 cost = 0.016708852723240852 cost = 0.012960446067154408 cost = 0.010525770485401154 cost = 0.008495906367897987 cost = 0.0067353141494095325 cost = 0.0057082874700427055 cost = 0.004624188877642155 cost = 0.004093789495527744 cost = 0.0038146725855767727 cost = 0.018593043088912964 cost = 0.010414039716124535 cost = 0.004842184949666262 hidden: kernel= [[1.1523403 1.181032 1.1671464 0.9644377 0.8377886 1.0919508 0.87283015 1.0875995 0.9677301 0.6194152 ]] bias = [-14.812331 -12.219926 -12.067375 -14.872566 -10.633507 -14.014006 -13.379829 -20.508204 -14.923473 -19.354435] output: kernel= [[ 2.0069902 ] [-1.0321712 ] [-0.8878887 ] [-2.0531905 ] [ 1.4293027 ] [ 2.1250408 ] [-1.578137 ] [ 4.141281 ] [-2.1264815 ] [-0.60681605]] bias = [-0.2812019] 

Código fonte

https://github.com/dprotopopov/nnfunc