Apresento a você a tradução de um capítulo do livro Hands-On Data Science with Anaconda
“Análise preditiva de dados - modelagem e validação”
Nosso principal objetivo na condução de várias análises de dados é procurar padrões para prever o que pode acontecer no futuro. Para o mercado de ações, pesquisadores e especialistas realizam vários testes para entender os mecanismos de mercado. Nesse caso, você pode fazer muitas perguntas. Qual será o nível do índice de mercado nos próximos cinco anos? Qual será a próxima faixa de preço para a IBM? A volatilidade do mercado aumentará ou diminuirá no futuro? Qual seria o efeito se os governos mudarem suas políticas tributárias? Quais são os ganhos e perdas em potencial se um país iniciar uma guerra comercial com outro? Como prevemos o comportamento do consumidor analisando algumas variáveis relacionadas? Podemos prever a probabilidade de um aluno se formar com sucesso? Podemos encontrar uma conexão entre o comportamento específico de uma doença em particular?
Portanto, consideraremos os seguintes tópicos:
- Compreendendo a análise preditiva de dados
- Conjuntos de dados úteis
- Previsão de eventos futuros
- Seleção de modelo
- Teste de Causalidade de Granger
Compreendendo a análise preditiva de dados
As pessoas podem ter muitas perguntas sobre eventos futuros.
- Um investidor, se conseguir prever o movimento futuro dos preços das ações, poderá obter um grande lucro.
- As empresas, se pudessem prever a tendência de seus produtos, poderiam aumentar o preço de suas ações e sua participação de mercado.
- Os governos, se pudessem prever o impacto de uma população em envelhecimento na sociedade e na economia, teriam mais incentivos para desenvolver melhores políticas em termos de orçamento do Estado e outras decisões estratégicas relevantes.
- As universidades, se pudessem entender bem a demanda do mercado em termos de qualidade e habilidades definidas para seus graduados, poderiam desenvolver um conjunto de programas melhores ou lançar novos programas para atender às necessidades futuras da força de trabalho.
Para um melhor prognóstico, os pesquisadores devem considerar muitas questões. Por exemplo, os dados de amostra são muito pequenos? Como remover variáveis ausentes? Esse conjunto de dados é tendencioso em termos de procedimentos de coleta de dados? Como nos sentimos sobre extremos ou emissões? O que é sazonalidade e como lidamos com isso? Quais modelos devemos usar? Este capítulo abordará alguns desses problemas. Vamos começar com um conjunto de dados útil.
Conjuntos de dados úteis
Uma das melhores fontes de dados é o
Repositório de Aprendizado de Máquina da
UCI . Tendo visitado o site, veremos a seguinte lista:

Por exemplo, se você selecionar o primeiro conjunto de dados (Abalone), veremos o seguinte. Para economizar espaço, apenas a parte superior é exibida:

A partir daqui, os usuários podem baixar o conjunto de dados e encontrar definições de variáveis. O código a seguir pode ser usado para carregar um conjunto de dados:
dataSet<-"UCIdatasets" path<-"http://canisius.edu/~yany/RData/" con<-paste(path,dataSet,".RData",sep='') load(url(con)) dim(.UCIdatasets) head(.UCIdatasets)
A saída correspondente é mostrada aqui:

Da conclusão anterior, sabemos que no conjunto de dados existem 427 observações (conjuntos de dados). Para cada uma delas, temos 7 funções relacionadas, como
Nome, Tipos de dados, Tarefa padrão, Tipos de atributo, N_Instances (número de instâncias),
N_Attributes (número de atributos) e
Ano . Uma variável chamada
Default_Task pode ser interpretada como o uso principal de cada conjunto de dados. Por exemplo, um primeiro conjunto de dados chamado
Abalone pode ser usado para
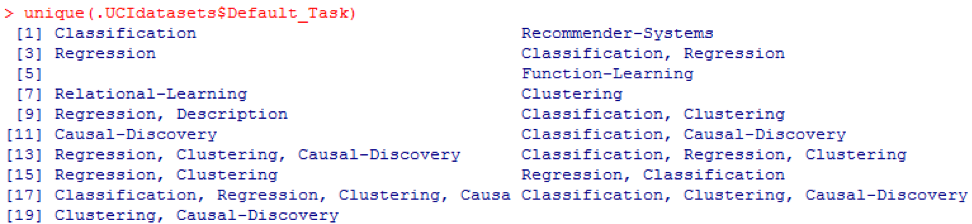
Classificação . A função
unique () pode ser usada para procurar todas as
tarefas padrão possíveis mostradas aqui:
Pacote R AppliedPredictiveModeling
Este pacote inclui muitos conjuntos de dados úteis que podem ser usados para este capítulo e outros. A maneira mais fácil de encontrar esses conjuntos de dados é com a função
help () mostrada aqui:
library(AppliedPredictiveModeling) help(package=AppliedPredictiveModeling)
Aqui mostramos alguns exemplos de carregamento desses conjuntos de dados. Para carregar um conjunto de dados, usamos a função
data () . Para o primeiro conjunto de dados chamado
abalone , temos o seguinte código:
library(AppliedPredictiveModeling) data(abalone) dim(abalone) head(abalone)
A saída é a seguinte:

Às vezes, um grande conjunto de dados inclui vários conjuntos de sub-dados:
library(AppliedPredictiveModeling) data(solubility) ls(pattern="sol")
[1] "solTestX" "solTestXtrans" "solTestY" [4] "solTrainX" "solTrainXtrans" "solTrainY"
Para carregar cada conjunto de dados, poderíamos usar as funções
dim () ,
head () ,
tail () e
summary () .
Análise de séries temporais
As séries temporais podem ser definidas como um conjunto de valores obtidos em momentos consecutivos, geralmente com intervalos iguais entre eles. Existem diferentes períodos, como anual, trimestral, mensal, semanal e diário. Para séries temporais do PIB (produto interno bruto), geralmente usamos trimestralmente ou anualmente. Para cotações - frequências anuais, mensais e diárias. Usando o código a seguir, podemos obter dados do PIB dos EUA trimestralmente e por um período anual:
ath<-"http://canisius.edu/~yany/RData/" dataSet<-"usGDPannual" con<-paste(path,dataSet,".RData",sep='') load(url(con)) head(.usGDPannual)
YEAR GDP 1 1930 92.2 2 1931 77.4 3 1932 59.5 4 1933 57.2 5 1934 66.8 6 1935 74.3
dataSet<-"usGDPquarterly" con<-paste(path,dataSet,".RData",sep='') load(url(con)) head(.usGDPquarterly)
DATE GDP_CURRENT GDP2009DOLLAR 1 1947Q1 243.1 1934.5 2 1947Q2 246.3 1932.3 3 1947Q3 250.1 1930.3 4 1947Q4 260.3 1960.7 5 1948Q1 266.2 1989.5 6 1948Q2 272.9 2021.9
No entanto, temos muitas perguntas para análise de séries temporais. Por exemplo, do ponto de vista da macroeconomia, temos ciclos econômicos ou de negócios. Indústrias ou empresas podem ter sazonalidade. Por exemplo, usando a indústria agrícola, os agricultores gastam mais na primavera e no outono e menos no inverno. Para os varejistas, eles teriam um enorme fluxo de dinheiro no final do ano.
Para manipular séries temporais, poderíamos usar os muitos recursos úteis incluídos no pacote R, chamados
timeSeries . No exemplo, usamos os dados médios diários com uma frequência semanal:
library(timeSeries) data(MSFT) x <- MSFT by <- timeSequence(from = start(x), to = end(x), by = "week") y<-aggregate(x,by,mean)
Também poderíamos usar a função
head () para ver algumas observações:
head(x)
GMT Open High Low Close Volume 2000-09-27 63.4375 63.5625 59.8125 60.6250 53077800 2000-09-28 60.8125 61.8750 60.6250 61.3125 26180200 2000-09-29 61.0000 61.3125 58.6250 60.3125 37026800 2000-10-02 60.5000 60.8125 58.2500 59.1250 29281200 2000-10-03 59.5625 59.8125 56.5000 56.5625 42687000 2000-10-04 56.3750 56.5625 54.5000 55.4375 68226700
head(y)
GMT Open High Low Close Volume 2000-09-27 63.4375 63.5625 59.8125 60.6250 53077800 2000-10-04 59.6500 60.0750 57.7000 58.5500 40680380 2000-10-11 54.9750 56.4500 54.1625 55.0875 36448900 2000-10-18 53.0375 54.2500 50.8375 52.1375 50631280 2000-10-25 61.7875 64.1875 60.0875 62.3875 86457340 2000-11-01 66.1375 68.7875 65.8500 67.9375 53496000
Previsão de eventos futuros
Existem muitos métodos que poderíamos usar ao tentar prever o futuro, como média móvel, regressão, regressão automática, etc. Primeiro, vamos começar com o mais simples para a média móvel:
movingAverageFunction<- function(data,n=10){ out= data for(i in n:length(data)){ out[i] = mean(data[(i-n+1):i]) } return(out) }
No código anterior, o valor padrão para o número de períodos é 10. Poderíamos usar um conjunto de dados chamado MSFT incluído no pacote R chamado
timeSeries (consulte o código a seguir):
library(timeSeries) data(MSFT) p<-MSFT$Close
[1] 60.6250 61.3125 60.3125 59.1250 56.5625 55.4375
head(ma)
[1] 60.62500 61.31250 60.75000 60.25000 58.66667 57.04167
mean(p[1:3])
[1] 60.75
mean(p[2:4])
[1] 60.25
No modo manual, descobrimos que a média dos três primeiros valores de
x corresponde ao terceiro valor de
y . De certa forma, poderíamos usar uma média móvel para prever o futuro.
No exemplo a seguir, mostraremos como avaliar os retornos de mercado esperados no próximo ano. Aqui, usamos o índice S & P500 e o valor médio anual histórico como nossos valores esperados. Os primeiros comandos são usados para carregar um conjunto de dados relacionado chamado
.sp500monthly . O objetivo do programa é avaliar a média anual média e o intervalo de confiança de 90%:
library(data.table) path<-'http://canisius.edu/~yany/RData/' dataSet<-'sp500monthly.RData' link<-paste(path,dataSet,sep='') load(url(link))
[min mean max ]
cat(min2,ourMean,max2,"\n")
0.05032956 0.09022369 0.1301178
Como você pode ver nos resultados, o retorno anual médio histórico para o S & P500 é de 9%. Mas não podemos dizer que a rentabilidade do índice no próximo ano será de 9%, porque pode variar de 5% a 13%, e são enormes flutuações.
Sazonalidade
No exemplo a seguir, mostramos o uso de autocorrelação. Primeiro,
baixamos um pacote R chamado
astsa , que significa análise estatística de séries temporais aplicada. Em seguida, carregamos o PIB dos EUA com uma frequência trimestral:
library(astsa) path<-"http://canisius.edu/~yany/RData/" dataSet<-"usGDPquarterly" con<-paste(path,dataSet,".RData",sep='') load(url(con)) x<-.usGDPquarterly$DATE y<-.usGDPquarterly$GDP_CURRENT plot(x,y) diff4 = diff(y,4) acf2(diff4,24)
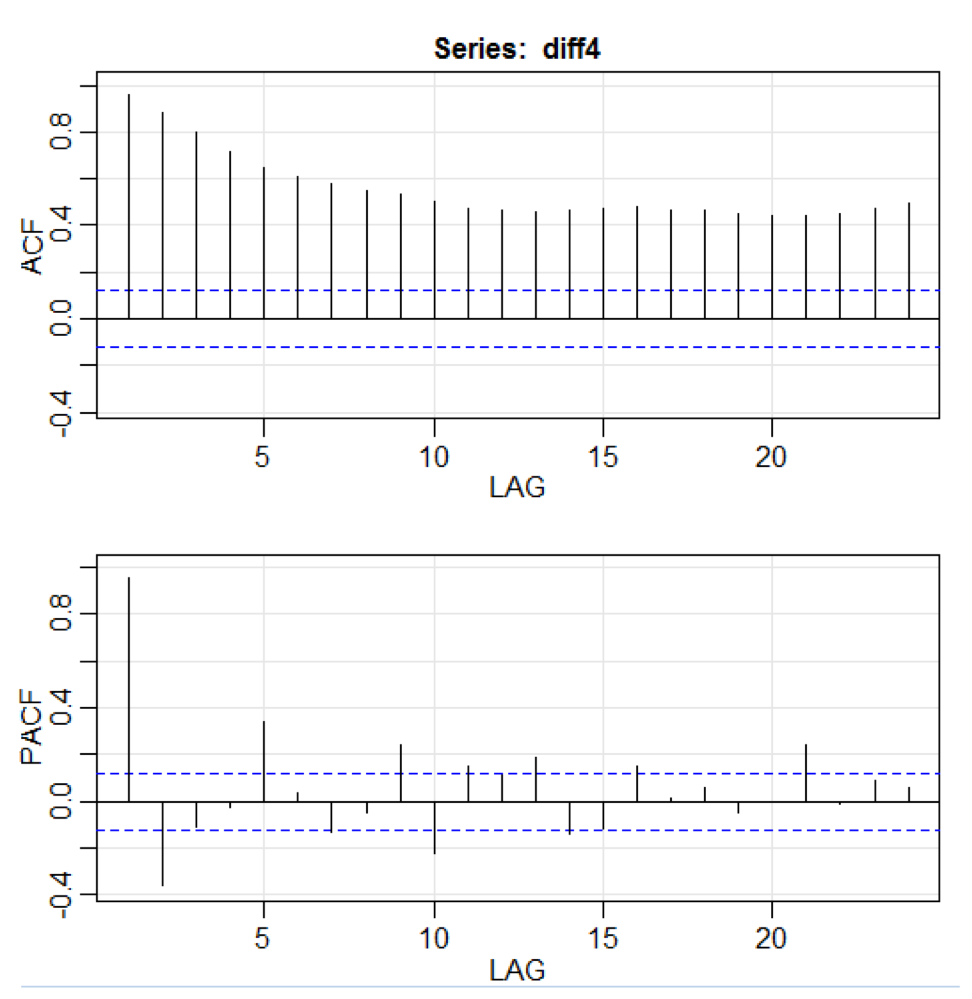
No código acima, a função
diff () aceita a diferença, por exemplo, o valor atual menos o valor anterior. Um segundo valor de entrada indica um atraso. Uma função chamada
acf2 () é usada para criar e imprimir as séries temporais do ACF e PACF. ACF significa função de autocovariância e PACF significa função de autocorrelação parcial. Os gráficos relevantes são mostrados aqui:
Visualização de componentes
Claramente, conceitos e conjuntos de dados seriam muito mais compreensíveis se pudéssemos usar gráficos. O primeiro exemplo mostra flutuações no PIB dos EUA nas últimas cinco décadas:
path<-"http://canisius.edu/~yany/RData/" dataSet<-"usGDPannual" con<-paste(path,dataSet,".RData",sep='') load(url(con)) title<-"US GDP" xTitle<-"Year" yTitle<-"US annual GDP" x<-.usGDPannual$YEAR y<-.usGDPannual$GDP plot(x,y,main=title,xlab=xTitle,ylab=yTitle)
A programação correspondente é mostrada aqui:
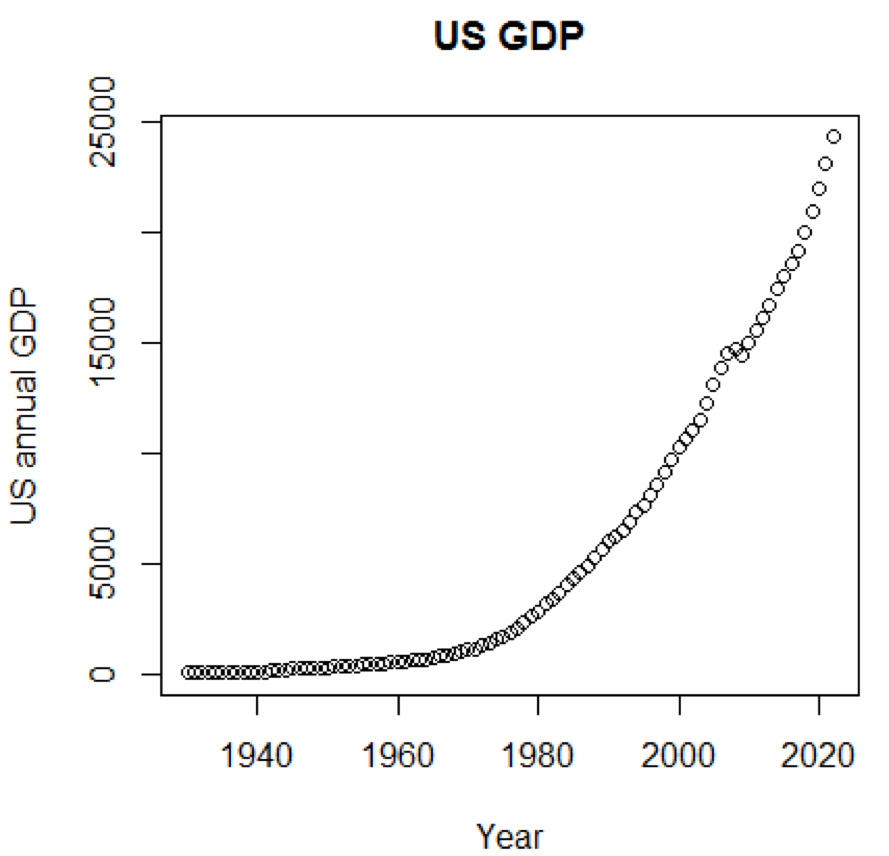
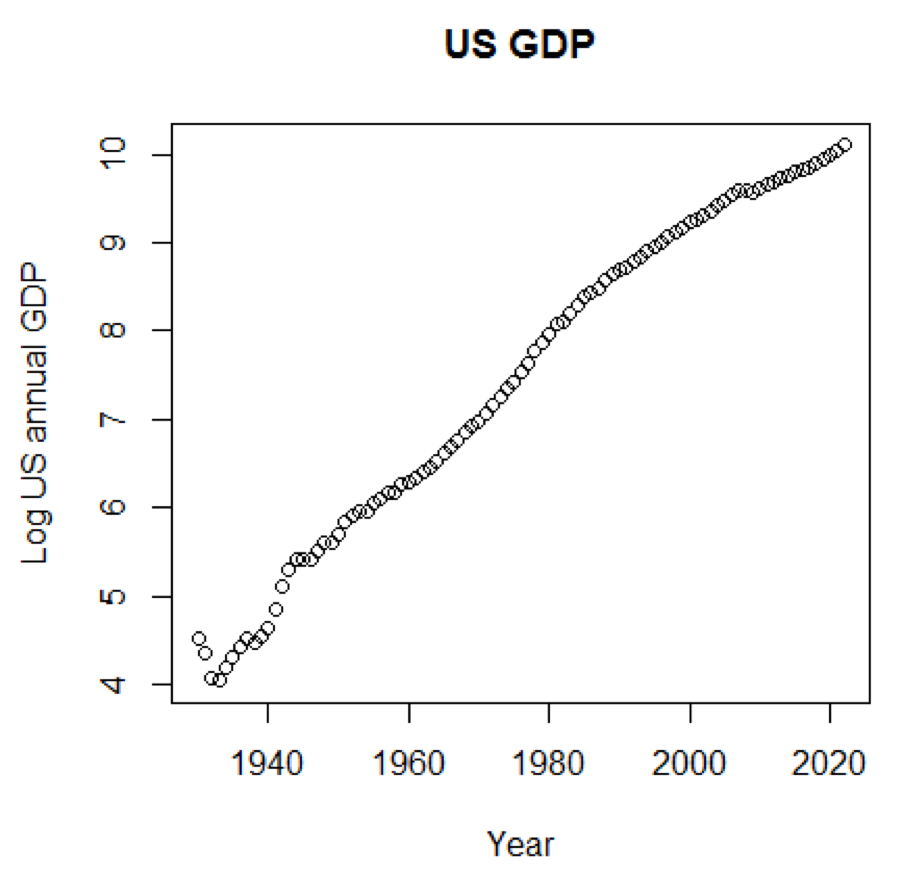
Se usássemos a escala logarítmica para o PIB, teríamos o seguinte código e gráfico:
yTitle<-"Log US annual GDP" plot(x,log(y),main=title,xlab=xTitle,ylab=yTitle)
O gráfico a seguir está próximo de uma linha reta:
Pacote R - LiblineaR
Este pacote é um modelo preditivo linear baseado na biblioteca LIBLINEAR C / C ++. Aqui está um exemplo de uso do conjunto de dados da
íris . O programa tenta prever a qual categoria uma planta pertence usando dados de treinamento:
library(LiblineaR) data(iris) attach(iris) x=iris[,1:4] y=factor(iris[,5]) train=sample(1:dim(iris)[1],100) xTrain=x[train,];xTest=x[-train,] yTrain=y[train]; yTest=y[-train] s=scale(xTrain,center=TRUE,scale=TRUE)
A conclusão é a seguinte. BCR é uma taxa de classificação equilibrada. Para esta aposta, quanto maior, melhor:
cat("Best model type is:",bestType,"\n")
Best model type is: 4
cat("Best cost is:",bestCost,"\n")
Best cost is: 1
cat("Best accuracy is:",bestAcc,"\n")
Best accuracy is: 0.98
print(res) yTest setosa versicolor virginica setosa 16 0 0 versicolor 0 17 0 virginica 0 3 14 print(BCR)
[1] 0.95
Pacote R - eclust
Este pacote é um cluster de orientação média para modelos preditivos interpretados em dados de alta dimensão. Primeiro, vejamos um conjunto de dados chamado
simdata que contém dados simulados para um pacote:
library(eclust) data("simdata") dim(simdata)
[1] 100 502
simdata[1:5, 1:6]
YE Gene1 Gene2 Gene3 Gene4 [1,] -94.131497 0 -0.4821629 0.1298527 0.4228393 0.36643188 [2,] 7.134990 0 -1.5216289 -0.3304428 -0.4384459 1.57602830 [3,] 1.974194 0 0.7590055 -0.3600983 1.9006443 -1.47250061 [4,] -44.855010 0 0.6833635 1.8051352 0.1527713 -0.06442029 [5,] 23.547378 0 0.4587626 -0.3996984 -0.5727255 -1.75716775
table(simdata[,"E"])
0 1 50 50
A conclusão anterior mostra que a dimensão dos dados é de 100 por 502.
Y é o vetor de resposta contínua e
E é a variável de ambiente binária para o método ECLUST.
E = 0 para não exposto (n = 50) e
E = 1 para exposto (n = 50).
O seguinte programa R avalia a transformação z de Fisher:
library(eclust) data("simdata") X = simdata[,c(-1,-2)] firstCorr<-cor(X[1:50,]) secondCorr<-cor(X[51:100,]) score<-u_fisherZ(n0=100,cor0=firstCorr,n1=100,cor1=secondCorr) dim(score)
[1] 500 500
score[1:5,1:5]
Gene1 Gene2 Gene3 Gene4 Gene5 Gene1 1.000000 -8.062020 6.260050 -8.133437 -7.825391 Gene2 -8.062020 1.000000 9.162208 -7.431822 -7.814067 Gene3 6.260050 9.162208 1.000000 8.072412 6.529433 Gene4 -8.133437 -7.431822 8.072412 1.000000 -5.099261 Gene5 -7.825391 -7.814067 6.529433 -5.099261 1.000000
Definimos a transformada z de Fisher. Supondo que tenhamos um conjunto de
n pares
x i e
y i , podemos estimar sua correlação usando a seguinte fórmula:
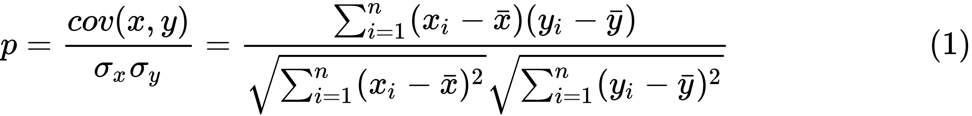
Aqui
p é a correlação entre duas variáveis e

e
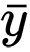
são médias amostrais para variáveis aleatórias
x e
y . O valor de
z é definido como:
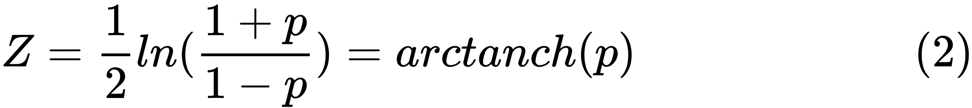 Ln
Ln é a função natural do logaritmo e
arctanh () é a função tangente hiperbólica inversa.
Seleção de modelo
Ao encontrar um bom modelo, às vezes nos deparamos com uma falta / excesso de dados. O exemplo a seguir é emprestado
daqui . Ele demonstra os problemas de trabalhar com isso e como podemos usar a regressão linear com recursos polinomiais para aproximar funções não lineares. Função especificada:
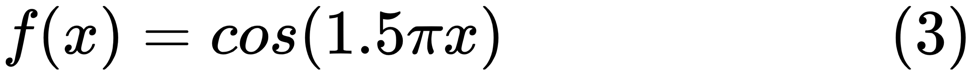
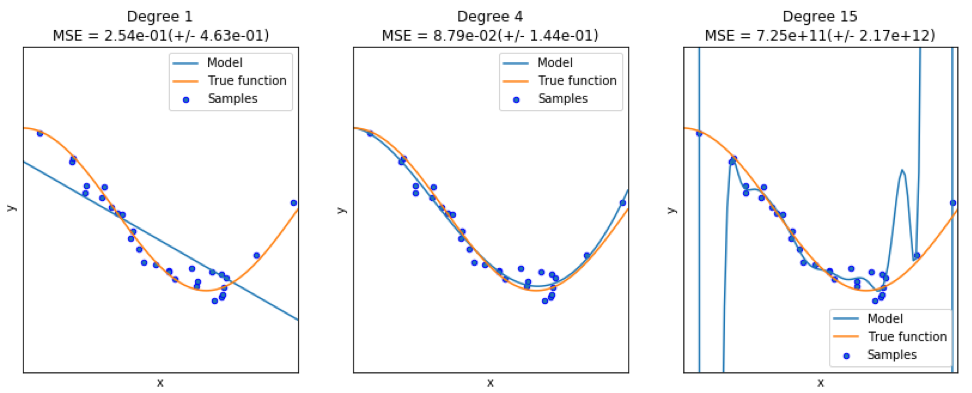
No próximo programa, tentamos usar modelos lineares e polinomiais para aproximar uma equação. Um código ligeiramente modificado é mostrado aqui. O programa ilustra o efeito da falta / excesso de oferta de dados no modelo:
import sklearn import numpy as np import matplotlib.pyplot as plt from sklearn.pipeline import Pipeline from sklearn.preprocessing import PolynomialFeatures from sklearn.linear_model import LinearRegression from sklearn.model_selection import cross_val_score
Os gráficos resultantes são mostrados aqui:
Pacote Python - model-catwalk
Um exemplo pode ser encontrado
aqui .
As primeiras linhas de código são mostradas aqui:
import datetime import pandas from sqlalchemy import create_engine from metta import metta_io as metta from catwalk.storage import FSModelStorageEngine, CSVMatrixStore from catwalk.model_trainers import ModelTrainer from catwalk.predictors import Predictor from catwalk.evaluation import ModelEvaluator from catwalk.utils import save_experiment_and_get_hash help(FSModelStorageEngine)
A conclusão correspondente é mostrada aqui. Para economizar espaço, apenas a parte superior é apresentada:
Help on class FSModelStorageEngine in module catwalk.storage: class FSModelStorageEngine(ModelStorageEngine) | Method resolution order: | FSModelStorageEngine | ModelStorageEngine | builtins.object | | Methods defined here: | | __init__(self, *args, **kwargs) | Initialize self. See help(type(self)) for accurate signature. | | get_store(self, model_hash) | | ----------------------------------------------------------------------
| Data descriptors inherited from ModelStorageEngine: | | __dict__ | dictionary for instance variables (if defined) | | __weakref__ | list of weak references to the object (if defined)
Pacote Python - sklearn
Como o
sklearn é um pacote muito útil, vale a pena mostrar mais exemplos do uso deste pacote. O exemplo dado aqui mostra como usar o pacote para classificar documentos por tópico, usando a abordagem de palavras-chave.
Este exemplo usa a matriz
scipy.sparse para armazenar objetos e demonstra vários classificadores que podem processar eficientemente matrizes esparsas. Este exemplo usa um conjunto de dados de 20 grupos de notícias. Será baixado automaticamente e armazenado em cache. O arquivo zip contém arquivos de entrada e pode ser baixado
aqui . O código está disponível
aqui . Para economizar espaço, apenas as primeiras linhas são mostradas:
import logging import numpy as np from optparse import OptionParser import sys from time import time import matplotlib.pyplot as plt from sklearn.datasets import fetch_20newsgroups from sklearn.feature_extraction.text import TfidfVectorizer from sklearn.feature_extraction.text import HashingVectorizer from sklearn.feature_selection import SelectFromModel
A saída correspondente é mostrada aqui:
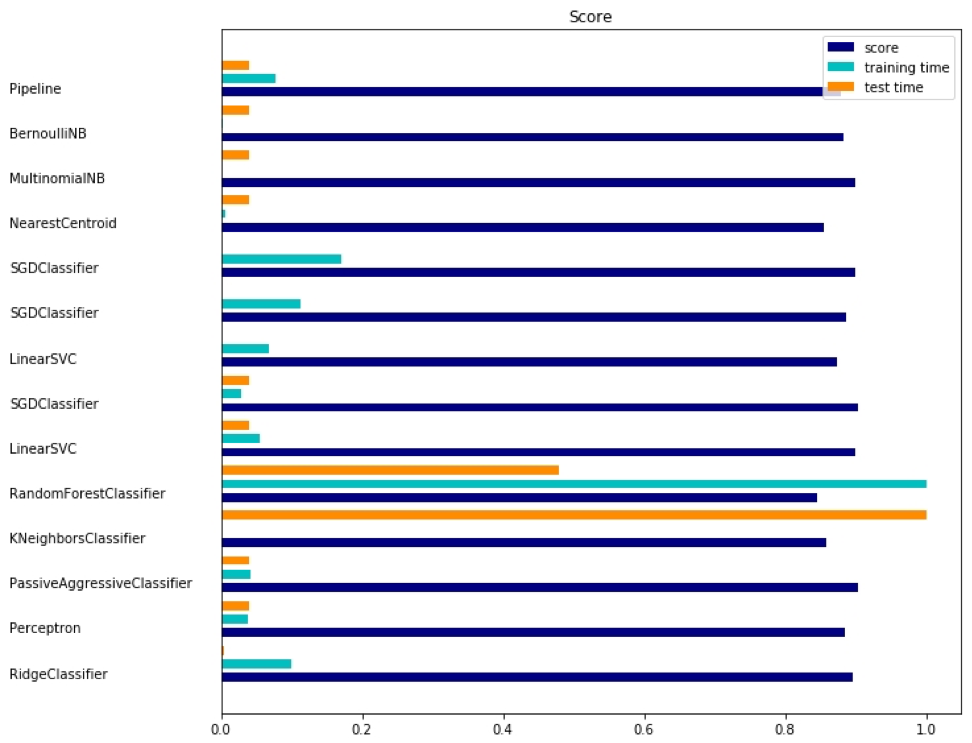
Existem três indicadores para cada método: avaliação, tempo de treinamento e tempo de teste.
Pacote Julia - QuantEcon
Tomemos, por exemplo, o uso de cadeias de Markov:
using QuantEcon P = [0.4 0.6; 0.2 0.8]; mc = MarkovChain(P) x = simulate(mc, 100000); mean(x .== 1)
Resultado:
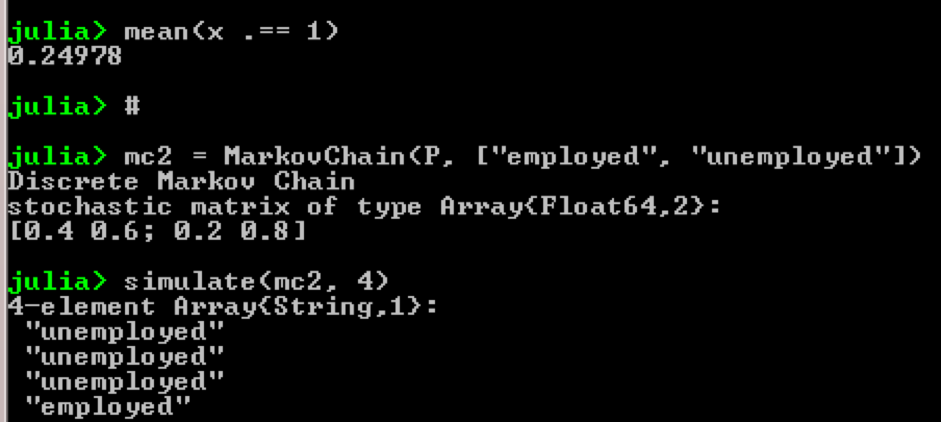
O objetivo do exemplo é ver como uma pessoa de um status econômico no futuro se transforma em outro. Primeiro, vamos olhar para o seguinte gráfico:
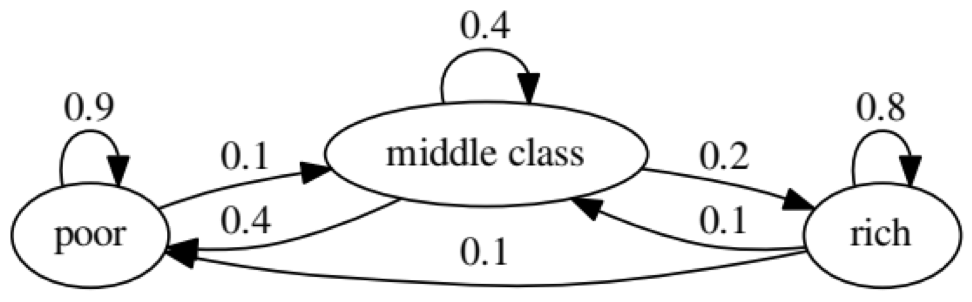
Vejamos o oval mais à esquerda com o status "ruim". 0,9 significa que uma pessoa com esse status tem 90% de chance de permanecer pobre e 10% entra na classe média. Pode ser representado pela seguinte matriz, zeros são onde não há arestas entre os nós:
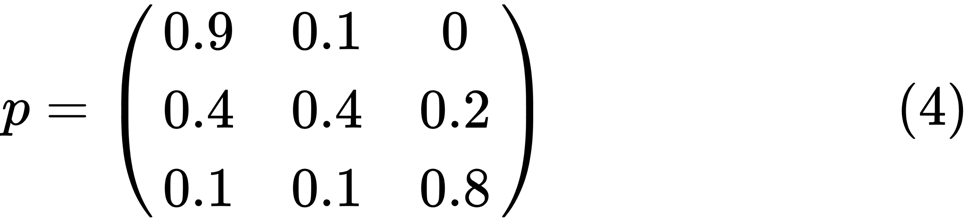
Diz-se que dois estados, x e y, são relacionados entre si se houver números inteiros positivos j e k, como:

Uma cadeia de Markov
P é chamada irredutível se todos os estados estiverem conectados; isto é, se
x e
y são relatados para cada (x, y). O código a seguir confirmará isso:
using QuantEcon P = [0.9 0.1 0.0; 0.4 0.4 0.2; 0.1 0.1 0.8]; mc = MarkovChain(P) is_irreducible(mc)
O gráfico a seguir representa um caso extremo, pois o status futuro de uma pessoa pobre será 100% ruim:

O código a seguir também confirmará isso, pois o resultado será
falso :
using QuantEcon P2 = [1.0 0.0 0.0; 0.1 0.8 0.1; 0.0 0.2 0.8]; mc2 = MarkovChain(P2) is_irreducible(mc2)
Teste de Causalidade de Granger
O teste de causalidade de Granger é usado para determinar se uma série temporal é um fator e fornece informações úteis para prever a segunda. O código a seguir usa um
conjunto de dados chamado
ChickEgg como uma ilustração. O conjunto de dados possui duas colunas, o número de galinhas e o número de ovos, com um registro de data e hora:
library(lmtest) data(ChickEgg) dim(ChickEgg)
[1] 54 2
ChickEgg[1:5,]
chicken egg [1,] 468491 3581 [2,] 449743 3532 [3,] 436815 3327 [4,] 444523 3255 [5,] 433937 3156
A questão é: podemos usar o número de ovos este ano para prever o número de galinhas no próximo ano?
Nesse caso, o número de galinhas será o motivo de Granger para o número de ovos. Se não for esse o caso, dizemos que o número de galinhas não é uma razão Granger para o número de ovos. Aqui está o código relevante:
library(lmtest) data(ChickEgg) grangertest(chicken~egg, order = 3, data = ChickEgg)
Granger causality test Model 1: chicken ~ Lags(chicken, 1:3) + Lags(egg, 1:3) Model 2: chicken ~ Lags(chicken, 1:3) Res.Df Df F Pr(>F) 1 44 2 47 -3 5.405 0.002966 ** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
No modelo 1, tentamos usar os atrasos dos pintinhos mais os atrasos dos ovos para explicar o número de pintinhos.
Porque Se o valor de
P é muito pequeno (é significativo em 0,01), dizemos que o número de ovos é a razão de Granger para o número de galinhas.
O teste a seguir mostra que os dados sobre galinhas não podem ser usados para prever o seguinte período:
grangertest(egg~chicken, order = 3, data = ChickEgg)
Granger causality test Model 1: egg ~ Lags(egg, 1:3) + Lags(chicken, 1:3) Model 2: egg ~ Lags(egg, 1:3) Res.Df Df F Pr(>F) 1 44 2 47 -3 0.5916 0.6238
No exemplo a seguir, verificamos a lucratividade da IBM e do S & P500 para descobrir que eles são motivo de Granger para outro.
Primeiro, definimos a função yield:
ret_f<-function(x,ticker=""){ n<-nrow(x) p<-x[,6] ret<-p[2:n]/p[1:(n-1)]-1 output<-data.frame(x[2:n,1],ret) name<-paste("RET_",toupper(ticker),sep='') colnames(output)<-c("DATE",name) return(output) }
>x<-read.csv("http://canisius.edu/~yany/data/ibmDaily.csv",header=T) ibmRet<-ret_f(x,"ibm") x<-read.csv("http://canisius.edu/~yany/data/^gspcDaily.csv",header=T) mktRet<-ret_f(x,"mkt") final<-merge(ibmRet,mktRet) head(final)
DATE RET_IBM RET_MKT 1 1962-01-03 0.008742545 0.0023956877 2 1962-01-04 -0.009965497 -0.0068887673 3 1962-01-05 -0.019694350 -0.0138730891 4 1962-01-08 -0.018750380 -0.0077519519 5 1962-01-09 0.011829467 0.0004340133 6 1962-01-10 0.001798526 -0.0027476933
Agora a função pode ser chamada com valores de entrada. O objetivo do programa é testar se podemos usar defasagens de mercado para explicar a lucratividade da IBM. Da mesma forma, verificamos para explicar o atraso da IBM na receita de mercado:
library(lmtest) grangertest(RET_IBM ~ RET_MKT, order = 1, data =final)
Granger causality test Model 1: RET_IBM ~ Lags(RET_IBM, 1:1) + Lags(RET_MKT, 1:1) Model 2: RET_IBM ~ Lags(RET_IBM, 1:1) Res.Df Df F Pr(>F) 1 14149 2 14150 -1 24.002 9.729e-07 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Os resultados mostram que o S & P500 pode ser usado para explicar a lucratividade da IBM para o próximo período, uma vez que é estatisticamente significativo em 0,1%. O código a seguir verificará se o atraso da IBM explica a alteração no S & P500:
grangertest(RET_MKT ~ RET_IBM, order = 1, data =final)
Granger causality test Model 1: RET_MKT ~ Lags(RET_MKT, 1:1) + Lags(RET_IBM, 1:1) Model 2: RET_MKT ~ Lags(RET_MKT, 1:1) Res.Df Df F Pr(>F) 1 14149 2 14150 -1 7.5378 0.006049 ** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
O resultado sugere que, durante esse período, os retornos da IBM podem ser usados para explicar o índice S & P500 para o próximo período.