Visão geral do SVM (algoritmo de aprendizado de máquina)

Prefácio

Neste artigo, exploraremos vários aspectos do SVM:

• componente teórico da SVM;
• como o algoritmo funciona em amostras que não podem ser divididas em classes linearmente;
• Exemplo de Python e implementação do algoritmo na biblioteca do SciKit Learn.

Nos artigos a seguir, tentarei falar sobre o componente matemático desse algoritmo.

Como você sabe, as tarefas de aprendizado de máquina são divididas em duas categorias principais - classificação e regressão. Dependendo de qual dessas tarefas estamos enfrentando e de qual conjunto de dados temos para essa tarefa, escolhemos qual algoritmo usar.

O Support Vector Machines Method ou SVM (do English Support Vector Machines) é um algoritmo linear usado em problemas de classificação e regressão. Este algoritmo é amplamente utilizado na prática e pode resolver problemas lineares e não lineares. A essência das "Máquinas" dos vetores de suporte é simples: o algoritmo cria uma linha ou hiperplano que divide os dados em classes.

Teoria

A principal tarefa do algoritmo é encontrar a linha mais correta, ou hiperplano, dividindo os dados em duas classes. SVM é um algoritmo que recebe dados na entrada e retorna essa linha divisória.

Considere o seguinte exemplo. Suponha que tenhamos um conjunto de dados e queremos classificar e separar os quadrados vermelhos dos círculos azuis (digamos positivo e negativo). O principal objetivo desta tarefa será encontrar a linha "ideal" que separará essas duas classes.



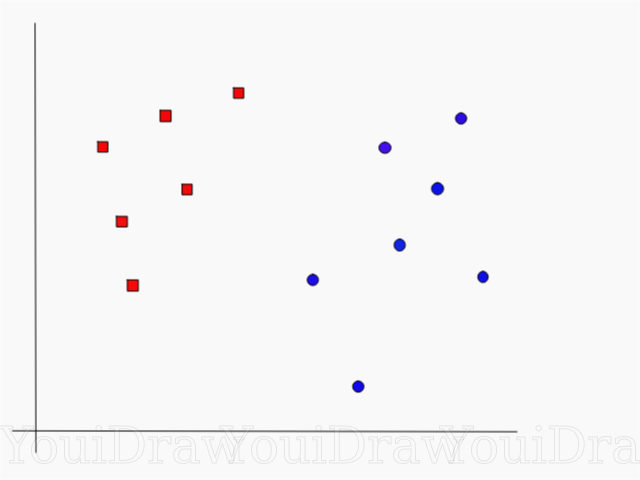
Encontre a linha perfeita, ou hiperplano, que divide o conjunto de dados em classes azul e vermelha.

À primeira vista, não é tão difícil, certo?

Mas, como você pode ver, não há uma linha única que resolveria esse problema. Podemos captar um número infinito de linhas que podem separar essas duas classes. Como exatamente o SVM encontra a linha "ideal" e o que é "ideal" em seu entendimento?

Dê uma olhada no exemplo abaixo e pense qual das duas linhas (amarela ou verde) melhor separa as duas classes e se encaixa na descrição do “ideal”?



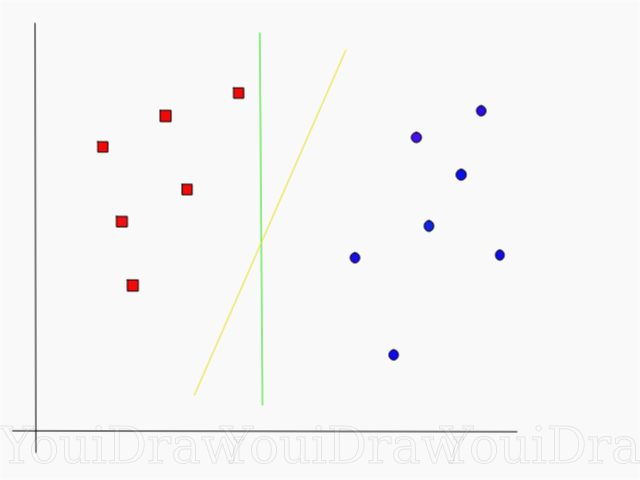
Qual linha separa melhor o conjunto de dados na sua opinião?

Se você escolheu a linha amarela, parabenizo: esta é a linha que o algoritmo escolheria. Neste exemplo, podemos entender intuitivamente que a linha amarela separa e, consequentemente, classifica as duas classes melhor que a verde.

No caso da linha verde - ela está localizada muito perto da classe vermelha. Apesar de ela ter classificado corretamente todos os objetos do conjunto de dados atual, essa linha não será generalizada - ela não se comportará tão bem quanto em um conjunto de dados desconhecido. A tarefa de encontrar uma separação generalizada de duas classes é uma das principais tarefas do aprendizado de máquina.

Como o SVM encontra a melhor linha

O algoritmo SVM é projetado de forma a procurar pontos no gráfico localizados diretamente na linha de separação mais próxima. Esses pontos são chamados vetores de referência. Em seguida, o algoritmo calcula a distância entre os vetores de suporte e o plano de divisão. Essa é a distância chamada lacuna. O objetivo principal do algoritmo é maximizar a distância da folga. O melhor hiperplano é considerado um hiperplano para o qual esse intervalo é o maior possível.



Muito simples, certo? Considere o exemplo a seguir, com um conjunto de dados mais complexo que não pode ser dividido linearmente.



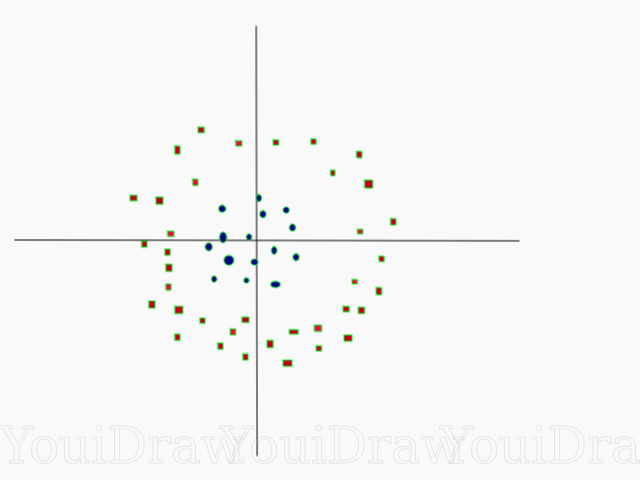
Obviamente, esse conjunto de dados não pode ser dividido linearmente. Não podemos desenhar uma linha reta que classifique esses dados. Mas, esse conjunto de dados pode ser dividido linearmente, adicionando uma dimensão adicional, que chamaremos de eixo Z. Imagine que as coordenadas no eixo Z sejam reguladas pela seguinte restrição:

$$

$$z = x² + y²$$

Assim, a ordenada Z é representada a partir do quadrado da distância do ponto até o início do eixo.
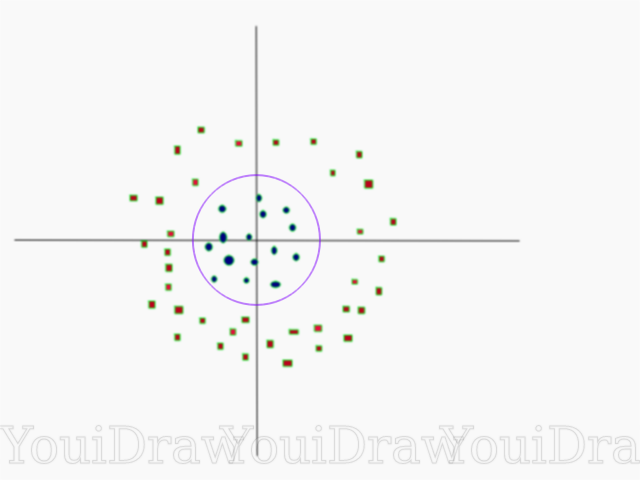
Abaixo está uma visualização do mesmo conjunto de dados no eixo Z.



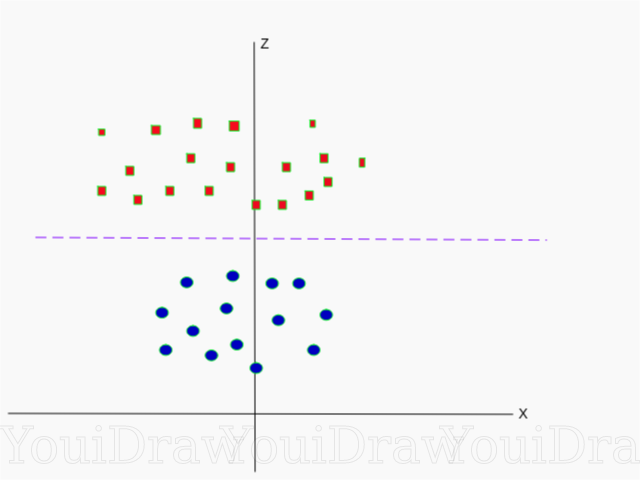
Agora os dados podem ser divididos linearmente. Suponha que a linha magenta que separa os dados z = k, onde k é uma constante. Se

$$

$$z = x² + y²$$

então

$$

$$k = x² + y²$$

- fórmula circular. Assim, podemos projetar nosso divisor linear, de volta ao número original de dimensões da amostra, usando essa transformação.



Como resultado, podemos classificar um conjunto de dados não lineares adicionando uma dimensão adicional a ele e, em seguida, devolvê-lo à sua forma original usando transformação matemática. No entanto, nem todos os conjuntos de dados são tão fáceis de iniciar essa transformação. Felizmente, a implementação desse algoritmo na biblioteca sklearn resolve esse problema para nós.

Hyperplane

Agora que nos familiarizamos com a lógica do algoritmo, passamos à definição formal de um hiperplano

Um hiperplano é um subplano n-1 dimensional em um espaço euclidiano n-dimensional que divide o espaço em duas partes separadas.

Por exemplo, imagine que nossa linha seja representada como um espaço euclidiano unidimensional (ou seja, nosso conjunto de dados está em uma linha reta). Selecione um ponto nesta linha. Este ponto dividirá o conjunto de dados, no nosso caso a linha, em duas partes. A linha tem uma medida e o ponto tem 0 medidas. Portanto, um ponto é um hiperplano de uma linha.

Para o conjunto de dados bidimensional que conhecemos anteriormente, a linha divisória era o mesmo hiperplano. Simplificando, para um espaço n-dimensional, há um hiperplano n-1 dimensional dividindo esse espaço em duas partes.

CÓDIGO

import numpy as np X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]]) y = np.array([1, 1, 2, 2]) 

Os pontos são representados como uma matriz de X e as classes às quais pertencem como uma matriz de y.
Agora vamos treinar nosso modelo com esta amostra. Neste exemplo, defino o parâmetro linear do "kernel" do classificador (kernel).

 from sklearn.svm import SVC clf = SVC(kernel='linear') clf = SVC.fit(X, y) 

Previsão de classe de um novo objeto

 prediction = clf.predict([[0,6]]) 

Parameter Setting

Parâmetros são os argumentos que você passa ao criar o classificador. Abaixo, forneci algumas das configurações SVM personalizadas mais importantes:

"C"

Este parâmetro ajuda a ajustar essa linha tênue entre "suavidade" e a precisão da classificação de objetos na amostra de treinamento. Quanto maior o valor "C", mais objetos no conjunto de treinamento serão classificados corretamente.



Neste exemplo, existem vários limites de decisão que podemos definir para esta amostra específica. Preste atenção ao limite de decisão direto (apresentado no gráfico como uma linha verde). É bastante simples e, por esse motivo, vários objetos foram classificados incorretamente. Esses pontos que foram classificados incorretamente são chamados de discrepantes nos dados.

Também podemos ajustar os parâmetros de forma que, no final, obtenha uma linha mais curva (limite de decisão em azul claro), que classificará absolutamente todos os dados da amostra de treinamento corretamente. Obviamente, nesse caso, as chances de nosso modelo ser capaz de generalizar e mostrar resultados igualmente bons em novos dados são catastroficamente pequenas. Portanto, se você estiver tentando obter precisão ao treinar o modelo, deve procurar algo mais uniforme e direto. Quanto maior o número "C", mais emaranhado o hiperplano estará no seu modelo, mas maior será o número de objetos classificados corretamente no conjunto de treinamento. Portanto, é importante “torcer” os parâmetros do modelo para um conjunto de dados específico, a fim de evitar reciclagem, mas, ao mesmo tempo, obter alta precisão.

Gamma

Na documentação oficial, a biblioteca SciKit Learn diz que a gama determina até que ponto cada um dos elementos do conjunto de dados influencia na determinação da "linha ideal". Quanto menor a gama, mais elementos, mesmo aqueles que estão longe o suficiente da linha divisória, participam do processo de escolha dessa mesma linha. Se a gama for alta, o algoritmo “confiará” apenas nos elementos que estão mais próximos da própria linha.
Se o nível gama estiver muito alto, apenas os elementos mais próximos à linha participarão do processo de tomada de decisão no local da linha. Isso ajudará a ignorar os valores discrepantes nos dados. O algoritmo SVM é projetado para que os pontos localizados mais próximos entre si tenham mais peso ao tomar uma decisão. No entanto, com a configuração correta de “C” e “gama”, é possível obter um resultado ideal que criará um hiperplano mais linear que ignora valores extremos e, portanto, é mais generalizável.

Conclusão

Espero sinceramente que este artigo tenha ajudado você a entender a essência do trabalho do SVM ou o Método do vetor de referência. Espero de você quaisquer comentários e conselhos. Nas publicações subsequentes, falarei sobre o componente matemático do SVM e os problemas de otimização.

Fontes:
Documentação oficial do SVM no SciKit Learn
TowardsDataScience Blog
Siraj Raval: Máquinas de vetores de suporte
Introdução ao Machine Learning Udacity SVM: vídeo do curso Gamma
Wikipedia: SVM