Fonte : Licença da Wikipedia CC-BY-SA 3.0

Se você costuma viajar de transporte público, provavelmente já se deparou com esta situação:

Você pára. Está escrito que o ônibus opera a cada 10 minutos. Anote o tempo ... Finalmente, após 11 minutos, o ônibus chega e o pensamento: por que sou sempre azarado?

Em teoria, se os ônibus chegarem a cada 10 minutos e você chegar em um horário aleatório, a espera média deverá ser de aproximadamente 5 minutos. Mas, na realidade, os ônibus não chegam dentro do cronograma, então você pode esperar mais. Acontece que, com algumas suposições razoáveis, pode-se chegar a uma conclusão surpreendente:

Ao esperar um ônibus que chega em média a cada 10 minutos, seu tempo médio de espera é de 10 minutos.

Isto é o que às vezes é chamado de paradoxo do tempo de espera .

Eu já tive uma idéia antes e sempre me perguntei se isso é realmente verdade ... quanto essas "suposições razoáveis" correspondem à realidade? Neste artigo, examinamos o paradoxo da latência em termos de modelagem e argumentos probabilísticos e, em seguida, examinamos alguns dos dados reais de ônibus em Seattle para (espero) resolver o paradoxo de uma vez por todas.

Inspeção do paradoxo

Se os ônibus chegarem exatamente a cada dez minutos, o tempo médio de espera será de 5 minutos. É fácil entender por que adicionar variações ao intervalo entre os ônibus aumenta o tempo médio de espera.

O paradoxo do tempo de espera é um caso especial de um fenômeno mais geral - o paradoxo da inspeção , que é discutido em detalhes no artigo sensato de Allen Downey, "O paradoxo da inspeção em todos os lugares" .

Em resumo, o paradoxo da inspeção surge sempre que a probabilidade de observar uma quantidade estiver relacionada à quantidade observada. Allen dá um exemplo de uma pesquisa com estudantes universitários sobre o tamanho médio de suas aulas. Embora a escola fale sinceramente do número médio de 30 alunos em um grupo, o tamanho médio do grupo do ponto de vista dos alunos é muito maior. O motivo é que, em turmas grandes (naturalmente), há mais alunos, o que é revelado durante a pesquisa.

No caso de um horário de ônibus com um intervalo declarado de 10 minutos, às vezes o intervalo entre as chegadas é superior a 10 minutos e, às vezes, mais curto. E se você parar aleatoriamente, é mais provável que encontre um intervalo maior que o menor. E, portanto, é lógico que o intervalo médio entre os intervalos de espera seja maior que o intervalo médio entre os barramentos, porque intervalos maiores são mais comuns na amostra.

Mas o paradoxo da latência faz uma afirmação mais forte: se o espaçamento médio do barramento é $$$N$ minutos, o tempo médio de espera para passageiros é de $$$2N$ minutos. Isso pode ser verdade?

Simulação de latência

Para nos convencermos da razoabilidade disso, primeiro simulamos o fluxo de ônibus que chegam em média 10 minutos. Para maior precisão, colete uma amostra grande: um milhão de ônibus (ou cerca de 19 anos de tráfego contínuo de 10 minutos):

import numpy as np N = 1000000 # number of buses tau = 10 # average minutes between arrivals rand = np.random.RandomState(42) # universal random seed bus_arrival_times = N * tau * np.sort(rand.rand(N)) 

Verifique se o intervalo médio está próximo de $$$\ tau = 10$ :

 intervals = np.diff(bus_arrival_times) intervals.mean() 

9.9999879601518398

Agora podemos simular a chegada de um grande número de passageiros em um ponto de ônibus durante esse período e calcular o tempo de espera que cada um deles experimenta. Encapsule o código em uma função para uso posterior:

 def simulate_wait_times(arrival_times, rseed=8675309, # Jenny's random seed n_passengers=1000000): rand = np.random.RandomState(rseed) arrival_times = np.asarray(arrival_times) passenger_times = arrival_times.max() * rand.rand(n_passengers) # find the index of the next bus for each simulated passenger i = np.searchsorted(arrival_times, passenger_times, side='right') return arrival_times[i] - passenger_times 

Em seguida, simulamos o tempo de espera e calculamos a média:

 wait_times = simulate_wait_times(bus_arrival_times) wait_times.mean() 

10.001584206227317

O tempo médio de espera é de aproximadamente 10 minutos, como o paradoxo previu.

Indo mais fundo: probabilidades e processos de Poisson

Como simular tal situação?

De fato, este é um exemplo de um paradoxo da inspeção, em que a probabilidade de observar um valor está relacionada ao próprio valor. Denotar por $$$p (T)$ espaçamento $$$T$ entre os ônibus quando eles chegam ao ponto de ônibus. Nesse registro, o valor esperado da hora de chegada será:

$$

$$E [T] = \ int_0 ^ \ infty T ~ p (T) ~ dT$$

Na simulação anterior, selecionamos $$$E [T] = \ tau = 10$ minutos.

Quando um passageiro chega a um ponto de ônibus a qualquer momento, a probabilidade de tempo de espera dependerá não apenas $$$p (T)$ mas também de $$$T$ : quanto maior o intervalo, maior número de passageiros.

Assim, podemos escrever a distribuição do tempo de chegada do ponto de vista dos passageiros:

$$

$$p_ {exp} (T) \ propto para T ~ p (T)$$

A constante de proporcionalidade é derivada da normalização da distribuição:

$$

$$p_ {exp} (T) = \ frac {T ~ p (T)} {\ int_0 ^ \ infty T ~ p (T) ~ dT}$$

Simplifica para

$$

$$p_ {exp} (T) = \ frac {T ~ p (T)} {E [T]}$$

Então o tempo de espera $$$E [W]$ será metade do intervalo esperado para os passageiros, para que possamos gravar

$$

$$E [W] = \ frac {1} {2} E_ {exp} [T] = \ frac {1} {2} \ int_0 ^ \ infty T ~ p_ {exp} (T) ~ dT$$

que pode ser reescrito de uma maneira mais compreensível:

$$

$$E [W] = \ frac {E [T ^ 2]} {2E [T]}$$

e agora resta apenas escolher um formulário para $$$p (T)$ e calcule as integrais.

A escolha de p (T)

Tendo recebido um modelo formal, qual é uma distribuição razoável para $$$p (T)$ ? Vamos desenhar uma imagem da distribuição $$$p (T)$ dentro de nossas chegadas simuladas, plotando um histograma dos intervalos entre as chegadas:

 %matplotlib inline import matplotlib.pyplot as plt plt.style.use('seaborn') plt.hist(intervals, bins=np.arange(80), density=True) plt.axvline(intervals.mean(), color='black', linestyle='dotted') plt.xlabel('Interval between arrivals (minutes)') plt.ylabel('Probability density'); 

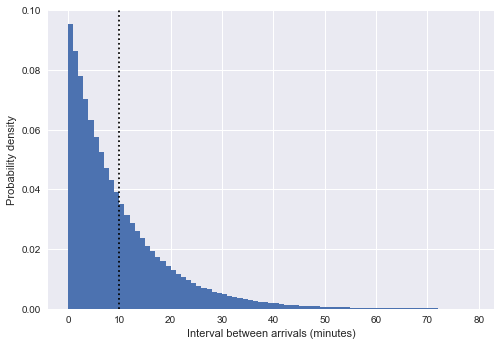
Aqui, a linha tracejada vertical mostra um intervalo médio de cerca de 10 minutos. Isso é muito semelhante a uma distribuição exponencial, e não por acidente: nossa simulação da hora de chegada do ônibus na forma de números aleatórios uniformes está muito próxima do processo de Poisson e, para esse processo, a distribuição de intervalos é exponencial.

(Nota: no nosso caso, este é apenas um expoente aproximado; de fato, os intervalos $$$T$ entre $$$N$ pontos uniformemente selecionados dentro de um intervalo de tempo $$$N \ tau$ combinar distribuição beta $$$T / (N \ tau) \ sim \ mathrm {Beta} [1, N]$ que está no grande limite $$$N$ aproximando $$$T \ sim \ mathrm {Exp} [1 / \ tau]$ . Para obter mais informações, você pode ler, por exemplo, uma postagem no StackExchange ou este tópico no Twitter ).

A distribuição exponencial de intervalos implica que o horário de chegada segue o processo de Poisson. Para verificar esse raciocínio, verificamos a presença de outra propriedade do processo de Poisson: se o número de chegadas em um período fixo de tempo é uma distribuição de Poisson. Para fazer isso, dividimos as chegadas simuladas em blocos de tempo:

 from scipy.stats import poisson # count the number of arrivals in 1-hour bins binsize = 60 binned_arrivals = np.bincount((bus_arrival_times // binsize).astype(int)) x = np.arange(20) # plot the results plt.hist(binned_arrivals, bins=x - 0.5, density=True, alpha=0.5, label='simulation') plt.plot(x, poisson(binsize / tau).pmf(x), 'ok', label='Poisson prediction') plt.xlabel('Number of arrivals per hour') plt.ylabel('frequency') plt.legend(); 

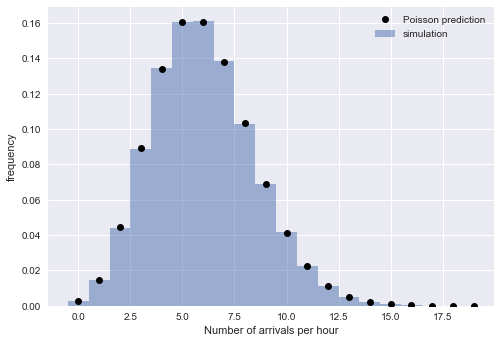
A estreita correspondência de valores empíricos e teóricos nos convence da correção de nossa interpretação: para grandes $$$N$ O tempo de chegada simulado é bem descrito pelo processo de Poisson, que implica intervalos distribuídos exponencialmente.

Isso significa que a distribuição de probabilidade pode ser escrita:

$$

$$p (T) = \ frac {1} {\ tau} e ^ {- T / \ tau}$$

Se substituirmos o resultado na fórmula anterior, encontraremos o tempo médio de espera para passageiros na parada:

$$

$$E [W] = \ frac {\ int_0 ^ \ infty T ^ 2 ~ e ^ {- T / \ tau}} {2 \ int_0 ^ \ infty T ~ e ^ {- T / \ tau}} = \ frac {2 \ tau ^ 3} {2 (\ tau ^ 2)} = \ tau$$

Para voos com chegadas pelo processo de Poisson, o tempo de espera esperado é idêntico ao intervalo médio entre as chegadas.

Esse problema pode ser argumentado da seguinte forma: o processo de Poisson é um processo sem memória , ou seja, a história dos eventos não tem nada a ver com o tempo esperado do próximo evento. Portanto, na chegada a um ponto de ônibus, o tempo médio de espera de um ônibus é sempre o mesmo: no nosso caso, são 10 minutos, independentemente de quanto tempo se passou desde o ônibus anterior! Não importa quanto tempo você está esperando: o tempo esperado para o próximo ônibus é sempre exatamente 10 minutos: no processo Poisson, você não recebe um "crédito" pelo tempo gasto em espera.

Tempo limite da realidade

O exposto acima é bom se as chegadas reais de ônibus forem realmente descritas pelo processo de Poisson, mas é isso?


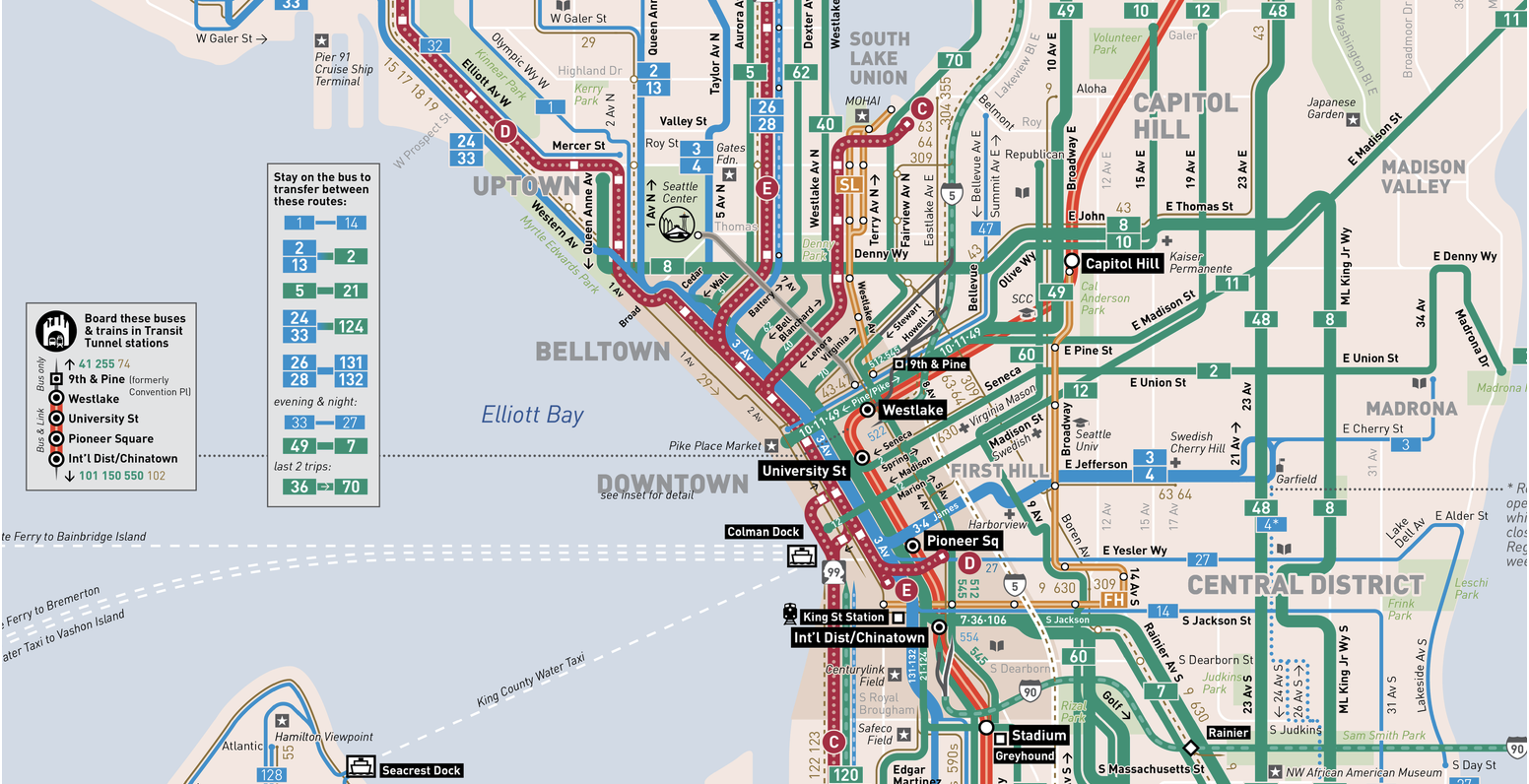Fonte: Esquema de transporte público de Seattle

Vamos tentar determinar como o paradoxo do tempo de espera é consistente com a realidade. Para fazer isso, examinaremos alguns dos dados disponíveis para download aqui: arrival_times.csv (arquivo CSV de 3 MB). O conjunto de dados contém os horários de chegada planejados e reais para os ônibus RapidRide C, D e E na 3ª e Pike Bus Stop, no centro de Seattle. Os dados foram registrados no segundo trimestre de 2016 (muito obrigado a Mark Hallenback, do Washington State Transportation Center, por esse arquivo!).

 import pandas as pd df = pd.read_csv('arrival_times.csv') df = df.dropna(axis=0, how='any') df.head() 

	OPD_DATE	VEHICLE_ID	RTE	DIR	TRIP_ID	STOP_ID	STOP_NAME	SCH_STOP_TM	ACT_STOP_TM
0 0	26-03-2016	6201	673	S	30908177	431	3RD AVE & PIKE ST (431)	01:11:57	01:13:19
1	26-03-2016	6201	673	S	30908033	431	3RD AVE & PIKE ST (431)	23:19:57	23:16:13
2	26-03-2016	6201	673	S	30908028	431	3RD AVE & PIKE ST (431)	21:19:57	21:18:46
3	26-03-2016	6201	673	S	30908019	431	3RD AVE & PIKE ST (431)	19:04:57	19:01:49
4	26-03-2016	6201	673	S	30908252	431	3RD AVE & PIKE ST (431)	16:42:57	16:42:39

Escolhi os dados do RapidRide, inclusive porque, na maior parte do dia, os ônibus circulam em intervalos regulares de 10 a 15 minutos, sem mencionar o fato de eu ser um passageiro frequente da rota C.

Limpeza de dados

Primeiro, faremos uma pequena limpeza de dados para convertê-los em uma visualização conveniente:

 # combine date and time into a single timestamp df['scheduled'] = pd.to_datetime(df['OPD_DATE'] + ' ' + df['SCH_STOP_TM']) df['actual'] = pd.to_datetime(df['OPD_DATE'] + ' ' + df['ACT_STOP_TM']) # if scheduled & actual span midnight, then the actual day needs to be adjusted minute = np.timedelta64(1, 'm') hour = 60 * minute diff_hrs = (df['actual'] - df['scheduled']) / hour df.loc[diff_hrs > 20, 'actual'] -= 24 * hour df.loc[diff_hrs < -20, 'actual'] += 24 * hour df['minutes_late'] = (df['actual'] - df['scheduled']) / minute # map internal route codes to external route letters df['route'] = df['RTE'].replace({673: 'C', 674: 'D', 675: 'E'}).astype('category') df['direction'] = df['DIR'].replace({'N': 'northbound', 'S': 'southbound'}).astype('category') # extract useful columns df = df[['route', 'direction', 'scheduled', 'actual', 'minutes_late']].copy() df.head() 

	Rota	Direção	Graph	Fato chegada	Atraso (min)
0 0	C	sul	2016-03-26 01:11:57	2016-03-26 01:13:19	1,366667
1	C	sul	2016-03-26 23:19:57	2016-03-26 23:16:13	-3.733333
2	C	sul	2016-03-26 21:19:57	2016-03-26 21:18:46	-1.183333
3	C	sul	2016-03-26 19:04:57	2016-03-26 19:01:49	-3.133333
4	C	sul	2016-03-26 16:42:57	2016-03-26 16:42:39	-0,300000

Até que horas são os ônibus?

Existem seis conjuntos de dados nesta tabela: direções norte e sul para cada rota C, D e E. Para se ter uma idéia de suas características, vamos construir um histograma do tempo real menos planejado de chegada para cada um desses seis:

 import seaborn as sns g = sns.FacetGrid(df, row="direction", col="route") g.map(plt.hist, "minutes_late", bins=np.arange(-10, 20)) g.set_titles('{col_name} {row_name}') g.set_axis_labels('minutes late', 'number of buses'); 

É lógico supor que os ônibus estejam mais próximos do horário no início do percurso e se desviem mais dele até o final. Os dados confirmam isso: nossa parada na rota sul C, bem como no norte e D e perto do início da rota, e na direção oposta, não muito longe do destino final.

Intervalos programados e observados

Dê uma olhada nos intervalos de ônibus observados e planejados para essas seis rotas. Vamos começar com a função groupby no Pandas para calcular estes intervalos:

 def compute_headway(scheduled): minute = np.timedelta64(1, 'm') return scheduled.sort_values().diff() / minute grouped = df.groupby(['route', 'direction']) df['actual_interval'] = grouped['actual'].transform(compute_headway) df['scheduled_interval'] = grouped['scheduled'].transform(compute_headway) 

 g = sns.FacetGrid(df.dropna(), row="direction", col="route") g.map(plt.hist, "actual_interval", bins=np.arange(50) + 0.5) g.set_titles('{col_name} {row_name}') g.set_axis_labels('actual interval (minutes)', 'number of buses'); 

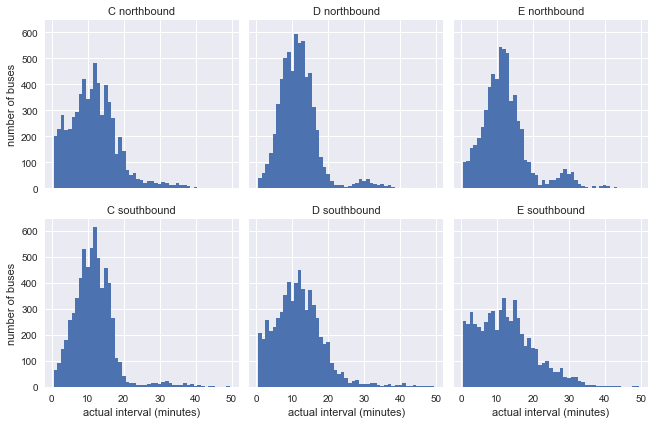
Já é evidente que os resultados não são muito semelhantes à distribuição exponencial do nosso modelo, mas isso ainda não diz nada: as distribuições podem ser afetadas por intervalos inconsistentes no gráfico.

Vamos repetir a construção dos diagramas, considerando os intervalos de chegada planejados e não os observados:

 g = sns.FacetGrid(df.dropna(), row="direction", col="route") g.map(plt.hist, "scheduled_interval", bins=np.arange(20) - 0.5) g.set_titles('{col_name} {row_name}') g.set_axis_labels('scheduled interval (minutes)', 'frequency'); 

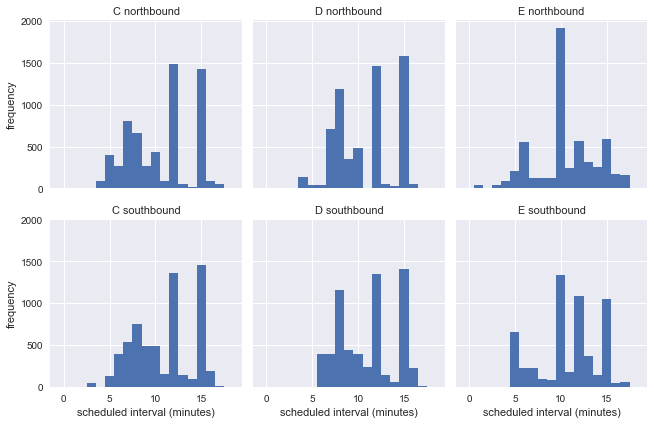
Isso mostra que, durante a semana, os ônibus circulam em intervalos diferentes, para que não possamos estimar a precisão do paradoxo do tempo de espera usando informações reais do ponto de ônibus.

Criando horários uniformes

Embora o cronograma oficial não forneça intervalos uniformes, existem vários intervalos de tempo específicos com um grande número de ônibus: por exemplo, quase 2.000 ônibus com rotas E indo para o norte com um intervalo planejado de 10 minutos. Para descobrir se o paradoxo da latência é aplicável, vamos agrupar os dados em rotas, direções e no intervalo planejado e, em seguida, empilhá-los novamente como se eles tivessem acontecido sequencialmente. Isso deve preservar todas as características relevantes dos dados de origem, facilitando a comparação direta com as previsões do paradoxo da latência.

 def stack_sequence(data): # first, sort by scheduled time data = data.sort_values('scheduled') # re-stack data & recompute relevant quantities data['scheduled'] = data['scheduled_interval'].cumsum() data['actual'] = data['scheduled'] + data['minutes_late'] data['actual_interval'] = data['actual'].sort_values().diff() return data subset = df[df.scheduled_interval.isin([10, 12, 15])] grouped = subset.groupby(['route', 'direction', 'scheduled_interval']) sequenced = grouped.apply(stack_sequence).reset_index(drop=True) sequenced.head() 

	Rota	Direção	Horário	Fato chegada	Atraso (min)	Fato intervalo	Intervalo agendado
0 0	C	norte	10.0	12.400000	2.400.000	NaN	10.0
1	C	norte	20,0	27.150000	7.150000	0,183333	10.0
2	C	norte	30,0	26.966667	-3.033333	14.566667	10.0
3	C	norte	40,0	35.516667	-4,483333	8.366667	10.0
4	C	norte	50,0	53.583333	3.583333	18.066667	10.0

Nos dados apagados, é possível fazer um gráfico da distribuição da aparência real dos ônibus ao longo de cada rota e direção com uma frequência de chegada:

 for route in ['C', 'D', 'E']: g = sns.FacetGrid(sequenced.query(f"route == '{route}'"), row="direction", col="scheduled_interval") g.map(plt.hist, "actual_interval", bins=np.arange(40) + 0.5) g.set_titles('{row_name} ({col_name:.0f} min)') g.set_axis_labels('actual interval (min)', 'count') g.fig.set_size_inches(8, 4) g.fig.suptitle(f'{route} line', y=1.05, fontsize=14) 

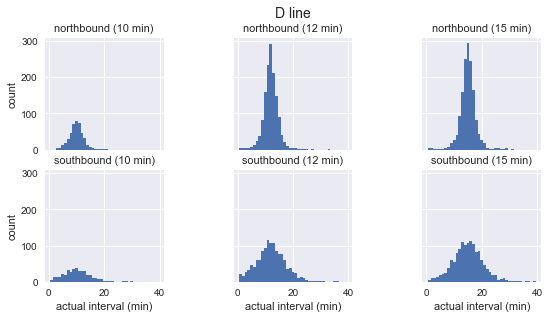
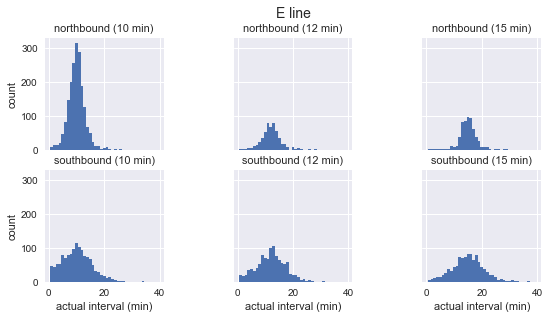
Vemos que, para cada rota, a distribuição dos intervalos observados é quase gaussiana. Ele atinge o pico próximo ao intervalo planejado e possui um desvio padrão menor no início da rota (sul para C, norte para D / E) e mais no final. Mesmo à vista, os intervalos reais de chegada definitivamente não correspondem à distribuição exponencial, que é a principal suposição na qual se baseia o paradoxo do tempo de espera.

Podemos usar a função de simulação do tempo de espera que usamos acima para encontrar o tempo médio de espera para cada rota, direção e horário de ônibus:

 grouped = sequenced.groupby(['route', 'direction', 'scheduled_interval']) sims = grouped['actual'].apply(simulate_wait_times) sims.apply(lambda times: "{0:.1f} +/- {1:.1f}".format(times.mean(), times.std())) 

  Intervalo agendado da direção da rota
 C norte 10,0 7,8 +/- 12,5
                       12,0 7,4 +/- 5,7
                       15,0 8,8 +/- 6,4
          sul 10,0 6,2 +/- 6,3
                       12,0 6,8 +/- 5,2
                       15,0 8,4 +/- 7,3
 D norte 10,0 6,1 +/- 7,1
                       12,0 6,5 +/- 4,6
                       15,0 7,9 +/- 5,3
          sul 10,0 6,7 +/- 5,3
                       12,0 7,5 +/- 5,9
                       15,0 8,8 +/- 6,5
 E norte 10,0 5,5 +/- 3,7
                       12,0 6,5 +/- 4,3
                       15,0 7,9 +/- 4,9
          sul 10,0 6,8 +/- 5,6
                       12,0 7,3 +/- 5,2
                       15,0 8,7 +/- 6,0
 Nome: real, dtype: object 

O tempo médio de espera, talvez um minuto ou dois, é mais da metade do intervalo planejado, mas não é igual ao intervalo planejado, como implica o paradoxo do tempo de espera. Em outras palavras, o paradoxo da inspeção é confirmado, mas o paradoxo do tempo de espera não é verdadeiro.

Conclusão

O paradoxo da latência foi um ponto de partida interessante para uma discussão que incluiu modelagem, teoria das probabilidades e comparação de suposições estatísticas com a realidade. Embora tenhamos confirmado que, no mundo real, as rotas de ônibus obedecem a algum tipo de paradoxo da inspeção, a análise acima mostra de forma bastante convincente: a principal suposição subjacente ao paradoxo do tempo de espera - que a chegada de ônibus segue as estatísticas do processo de Poisson - não é justificada.

Em retrospecto, isso não é surpreendente: o processo de Poisson é um processo sem memória que assume que a probabilidade de chegada é completamente independente do tempo desde a chegada anterior. De fato, um sistema de transporte público bem gerenciado possui horários especialmente estruturados para evitar esse comportamento: os ônibus não iniciam suas rotas em horários aleatórios durante o dia, mas iniciam de acordo com o horário escolhido para o transporte mais eficiente dos passageiros.

A lição mais importante é ter cuidado com as suposições que você faz sobre qualquer tarefa de análise de dados. Às vezes, o processo de Poisson é uma boa descrição para os dados da hora de chegada. Mas apenas porque um tipo de dados soa como outro tipo de dados não significa que as suposições permitidas para um sejam necessariamente válidas para o outro. Frequentemente, suposições que parecem corretas podem levar a conclusões que não são verdadeiras.