Há um ano e meio, publiquei o artigo
“Matemática nos dedos: métodos dos mínimos quadrados” , que recebeu uma resposta bastante decente, que, entre outros, consistia no fato de que eu propus desenhar uma coruja. Bem, desde uma coruja, você precisa explicá-la novamente. Em uma semana, exatamente sobre esse assunto, começarei a dar várias palestras para estudantes de geologia; Aproveito esta oportunidade, apresento aqui os principais pontos (adaptados) como um rascunho. Meu principal objetivo não é fornecer uma receita pronta de um livro sobre comida saborosa e saudável, mas explicar por que é assim e o que mais existe na seção correspondente, porque as conexões entre as diferentes seções da matemática são as mais interessantes!
No momento, pretendo quebrar o texto da seguinte maneira:
Vou aos mínimos quadrados um pouco de lado, através do princípio da máxima probabilidade, e requer orientação mínima na teoria das probabilidades. Este texto foi elaborado para o terceiro ano de nossa faculdade de geologia, o que significa (do ponto de vista do equipamento envolvido!) Que um estudante do ensino médio interessado com o zelo apropriado deve ser capaz de entendê-lo.
Qual é o som do teórico ou você acredita na teoria da evolução?
Um dia me perguntaram se acredito na teoria da evolução. Faça uma pausa agora, pense em como você responderá.

Pessoalmente, fiquei surpreso, respondi que considero crível e que a questão da fé não surge aqui. A teoria científica tem pouco a ver com fé. Em suma, a teoria apenas constrói um modelo do mundo ao nosso redor, não há necessidade de acreditar nela. Além disso,
o critério de Popper exige que uma teoria científica seja capaz de refutar. E também uma teoria sólida deve possuir, antes de tudo, poder preditivo. Por exemplo, se você modificar geneticamente as culturas de tal maneira que elas mesmas produzam pesticidas, é lógico que os insetos resistentes a elas apareçam. No entanto, é significativamente menos óbvio que esse processo pode ser retardado pelo crescimento de plantas comuns, lado a lado com as geneticamente modificadas. Com base na teoria da evolução, a simulação correspondente fez
essa previsão , e parece estar
confirmada .
E o que os mínimos quadrados têm a ver com isso?
Como mencionei anteriormente, irei aos mínimos quadrados através do princípio da máxima verossimilhança. Vamos ilustrar com um exemplo. Suponha que estejamos interessados em dados sobre o crescimento de pinguins, mas podemos medir apenas alguns desses lindos pássaros. É bastante lógico introduzir um modelo de distribuição de crescimento na tarefa - na maioria das vezes é normal. A distribuição normal é caracterizada por dois parâmetros - valor médio e desvio padrão. Para cada valor fixo dos parâmetros, podemos calcular a probabilidade de que exatamente essas medições que fizemos serão geradas. Além disso, variando os parâmetros, encontramos aqueles que maximizam a probabilidade.
Assim, para trabalhar com a máxima probabilidade, precisamos operar em termos da teoria das probabilidades. Um pouco mais baixo, nos dedos, definimos o conceito de probabilidade e probabilidade, mas primeiro eu gostaria de focar em outro aspecto. Surpreendentemente, raramente vejo pessoas pensando sobre a palavra "teoria" na frase "teoria das probabilidades".
O que é o teorizador da aprendizagem?
Com relação às origens, significados e escopo das estimativas de probabilidade, há um debate violento há mais de cem anos. Por exemplo,
Bruno De Finetti afirmou que a probabilidade nada mais é do que uma análise subjetiva da probabilidade de que algo aconteça e que essa probabilidade não existe fora da mente. Essa é a disposição de uma pessoa para apostar em algo que está acontecendo. Essa opinião é diretamente oposta à visão dos
clássicos / freventistas sobre a probabilidade de um resultado específico de um evento, no qual é assumido que o mesmo evento pode ser repetido várias vezes, e a "probabilidade" de um resultado específico está relacionada à frequência de um resultado específico cair durante testes repetidos. Além de subjetivistas e freventistas, também existem objetivistas que argumentam que as probabilidades são aspectos reais do universo, e não apenas descrições do grau de confiança do observador.
Seja como for, mas todas as três escolas científicas na prática usam o mesmo aparato baseado nos axiomas de Kolmogorov. Vamos dar um argumento indireto, de um ponto de vista subjetivista, a favor da teoria das probabilidades, construído sobre os axiomas de Kolmogorov. Damos os axiomas um pouco mais tarde, mas, para começar, assumiremos que temos uma casa de apostas que aceitará apostas na próxima Copa do Mundo. Vamos ter dois eventos: a = o time do Uruguai se tornará o campeão, b = o time alemão se tornará o campeão. A casa de apostas estima as chances da equipe uruguaia vencer em 40%, as chances da equipe alemã em 30%. Obviamente, a Alemanha e o Uruguai não podem vencer ao mesmo tempo, portanto a chance de a∧b é zero. Bem, ao mesmo tempo, a casa de apostas acredita que a probabilidade de Uruguai ou Alemanha (e não Argentina ou Austrália) vencerem é de 80%. Vamos escrever da seguinte forma:

Se o apostador afirma que seu grau de confiança no evento
a é 0,4, ou seja,
P (a) = 0,4, o jogador pode escolher se apostará a favor ou contra o de
a , valores de apostas compatíveis com o grau de confiança do apostador. Isso significa que o jogador pode apostar que o evento acontecerá apostando quatro rublos contra seis rublos da casa de apostas. Ou um jogador pode apostar seis rublos em vez de quatro rublos de uma casa de apostas que o evento não acontecerá.
Se o grau de confiança da casa de apostas não refletir com precisão o estado do mundo, podemos contar com o fato de que, a longo prazo, perderá dinheiro para jogadores cujas crenças são mais precisas. Além disso, neste exemplo em particular, o jogador tem uma estratégia na qual a casa de apostas
sempre perde dinheiro. Vamos ilustrar:

O jogador faz três apostas e, independentemente do resultado do campeonato, ele sempre vence. Observe que a consideração dos ganhos em princípio não inclui se o Uruguai ou a Alemanha são os favoritos do campeonato, a perda da casa de apostas é garantida! Essa situação foi liderada pelo fato de a casa de apostas não ter sido guiada pelos princípios da teoria das probabilidades, por ter violado o terceiro axioma de Kolmogorov, vamos trazer os três:
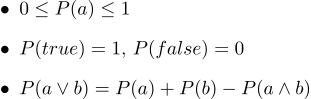
Em forma de texto, eles ficam assim:
- 1. Todas as probabilidades variam de 0 a 1
- 2. Certamente, declarações verdadeiras têm uma probabilidade de 1 e certamente uma probabilidade falsa de 0.
- 3. O terceiro axioma é o axioma da disjunção, é fácil entender intuitivamente, observando que os casos em que a afirmação a é verdadeira, juntamente com os casos em que b é verdadeira, certamente abrangem todos os casos em que a afirmação a∨b é verdadeira; mas na soma de dois conjuntos de casos, sua interseção ocorre duas vezes; portanto, é necessário subtrair P (a∧b).
Em 1931, de Finetti
provou uma afirmação muito forte:
Se o apostador é guiado por muitos graus de confiança, o que viola os axiomas da teoria da probabilidade, existe uma combinação de apostas de jogador que garante a perda do apostador (o jogador ganha) a cada aposta.
Os axiomas das probabilidades podem ser considerados como limitantes do conjunto de crenças probabilísticas que algum agente pode sustentar. Observe que seguir o apostador não implica os axiomas de Kolmogorov de que ele vencerá (deixaremos os problemas de comissão de lado), mas se você não segui-los, será garantido que ele perderá. Observe que outros argumentos foram apresentados em favor da aplicação de probabilidades; mas foi o sucesso
prático dos sistemas de raciocínio baseados na teoria das probabilidades que acabou sendo um incentivo atraente que causou uma revisão de muitas visões.
Então, abrimos um pouco o véu de
por que o Theorver pode fazer sentido, mas que tipo de objetos ele manipula? A teoria inteira é construída em apenas três axiomas; todos os três envolvem alguma função mágica
P. Além disso, olhando para esses axiomas, isso me lembra muito a função da área da forma. Vamos tentar ver se a área funciona para determinar a probabilidade.
Definimos a palavra "evento" como "um subconjunto de um quadrado de unidade". Definimos a palavra "probabilidade de um evento" como "a área do subconjunto correspondente". Grosso modo, temos um grande alvo de papelão e, tendo fechado os olhos, atiramos nele. As chances de uma bala cair em um determinado conjunto são diretamente proporcionais à área do conjunto. Um evento confiável nesse caso é o quadrado inteiro e, obviamente, falso, por exemplo, qualquer ponto do quadrado. Segue-se da nossa definição de probabilidade que é impossível chegar ao ponto perfeitamente (nossa bala é um ponto material). Eu realmente gosto de imagens e desenho muitas delas, e o teor teórico não é exceção! Vamos ilustrar todos os três axiomas:
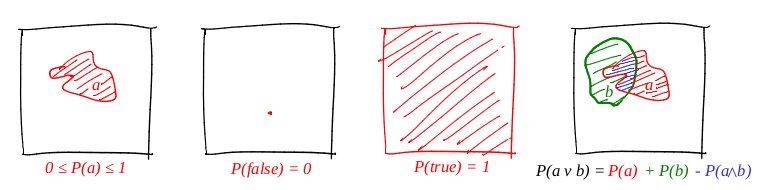
Portanto, o primeiro axioma é cumprido: a área é não negativa e não pode exceder unidades. Um evento confiável é o quadrado inteiro e deliberadamente falso é qualquer conjunto de área zero. E funciona perfeitamente com o disjuntor!
Credibilidade máxima com exemplos
Exemplo 1: Inversão de moeda
Vejamos o exemplo mais simples de um sorteio, também conhecido como
o esquema de Bernoulli .
N experimentos são realizados, em cada um dos quais um dos dois eventos pode ocorrer ("sucesso" ou "falha"), um com probabilidade
p e o segundo com probabilidade
1-p . Nossa tarefa é encontrar a probabilidade de obter exatamente
k sucessos nesses
n experimentos. Essa probabilidade nos dá a fórmula de Bernoulli:
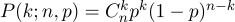
Pegue uma moeda comum (
p = 0,5 ), jogue-a dez vezes (
n = 10 ) e considere quantas vezes as caudas caem:
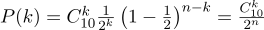
Aqui está um gráfico da densidade de probabilidade:
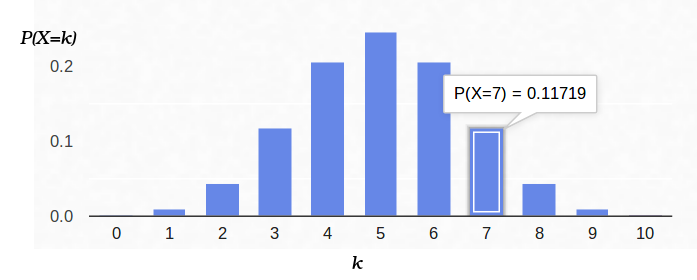
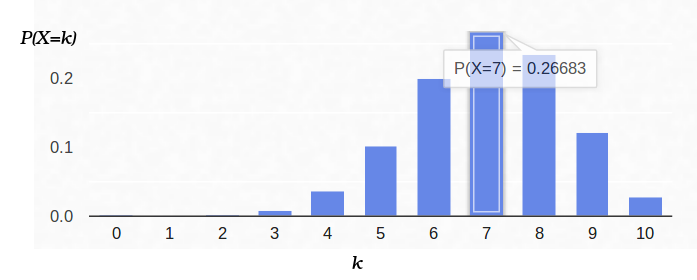
Assim, se fixamos a probabilidade do início de "sucesso" (0,5) e também registramos o número de experimentos (10), o número possível de "sucessos" pode ser qualquer número inteiro entre 0 e 10, no entanto, esses resultados não são igualmente prováveis. É óbvio que obter cinco "sucessos" é muito mais provável do que não um. Por exemplo, a probabilidade de contar sete caudas é de aproximadamente 12%.
Agora, vamos olhar para a mesma tarefa do outro lado. Temos uma moeda real, mas não sabemos sua distribuição da probabilidade a priori de "sucesso" / "fracasso". No entanto, podemos jogá-lo dez vezes e contar o número de "sucessos". Por exemplo, temos sete caudas. Como isso nos ajuda a avaliar
p ?
Podemos tentar corrigir
n = 10
ek = 7 na fórmula de Bernoulli, deixando
p um parâmetro livre:

Então a fórmula de Bernoulli pode ser interpretada como a
probabilidade do parâmetro estimado (neste caso,
p ). Eu até mudei a letra da função, agora é
L (da semelhança em inglês). Ou seja, a probabilidade é a probabilidade de gerar dados de observação (7 caudas de 10 experimentos) para um dado valor do (s) parâmetro (s).
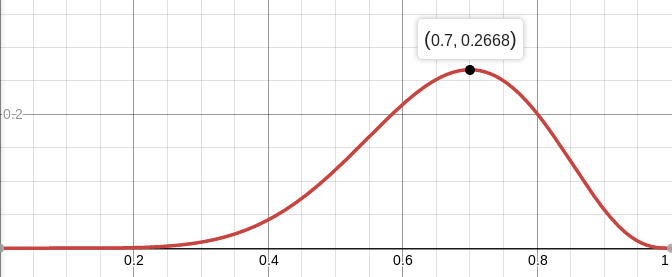
Por exemplo, a probabilidade de uma moeda equilibrada (
p = 0,5), desde que ocorram sete caudas em cada dez arremessos, é de aproximadamente 12%. Você pode plotar a função
L :
Então, estamos procurando um valor de parâmetros que maximize a probabilidade de obter essas observações que temos. Nesse caso em particular, temos a função de uma variável, estamos procurando seu máximo. Para facilitar a pesquisa, procurarei no máximo não
L , mas
log L. O logaritmo é uma função estritamente monotônica, portanto, maximizar um e o outro é exatamente a mesma coisa. E o logaritmo divide o produto em uma quantidade muito mais conveniente para diferenciar. Então, estamos procurando o máximo dessa função:

Para fazer isso, equiparamos sua derivada a zero:
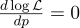
A derivada de log x = 1 / x, obtemos:

Ou seja, a probabilidade máxima (aproximadamente 27%) é alcançada em

Apenas no caso, calculamos a segunda derivada:
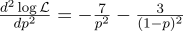
No ponto p = 0,7, é negativo, portanto esse ponto é realmente o máximo da função L.
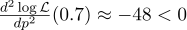
E aqui está a densidade de probabilidade para o esquema de Bernoulli com
p = 0,7:
Exemplo dois: ADC
Vamos imaginar que temos uma certa quantidade física constante que queremos medir, seja um comprimento com uma régua ou uma tensão com um voltímetro. Qualquer medida fornece uma
aproximação dessa quantidade, mas não a quantidade em si. Os métodos que descrevo aqui foram desenvolvidos por Gauss no final do século 18, quando ele mediu as órbitas dos corpos celestes.
Por exemplo, se medirmos a tensão da bateria N vezes, obtemos N medições diferentes. Qual levar? Isso é tudo! Então, vamos ter N quantidades Uj:
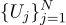
Suponha que cada medida Uj seja igual a um valor ideal, mais um ruído gaussiano, caracterizado por dois parâmetros - a posição do sino gaussiano e sua “largura”. Aqui está a densidade de probabilidade:
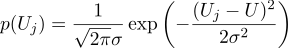
Ou seja, tendo N dados valores de Uj, nossa tarefa é encontrar esse parâmetro, U que maximize o valor da probabilidade. A credibilidade (imediatamente retiro o logaritmo) pode ser escrita da seguinte maneira:
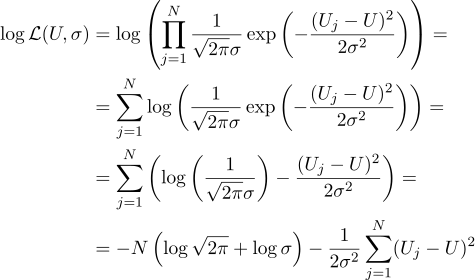
Bem, então tudo está estritamente como antes, equacionamos zero derivadas parciais em relação aos parâmetros que estamos procurando:
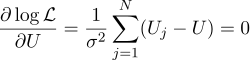
Concluímos que a estimativa mais provável da quantidade desconhecida U pode ser encontrada como a média de todas as medições:
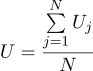
Bem, o parâmetro sigma mais provável é o desvio padrão usual:
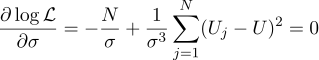

Valeu a pena se preocupar em obter uma média simples de todas as medidas na resposta? Para o meu gosto, valeu a pena. A propósito, calcular a média de várias medições de um valor constante para aumentar a precisão das medições é uma prática padrão. Por exemplo, a
média da ADC . A propósito, para esse ruído gaussiano não é necessário, basta que o ruído seja imparcial.
Exemplo três e, novamente, unidimensional
Continuamos a conversa, vamos dar o mesmo exemplo, mas complicamos um pouco. Queremos medir a resistência de um determinado resistor. Com a ajuda de uma fonte de alimentação de laboratório, somos capazes de passar um número padrão de amperes por ela e medir a tensão necessária para isso. Ou seja, teremos N pares de números (Ij, Uj) na entrada do nosso avaliador de resistência.
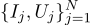
Desenhe esses pontos no gráfico; A lei de Ohm nos diz que estamos procurando a inclinação da linha azul.
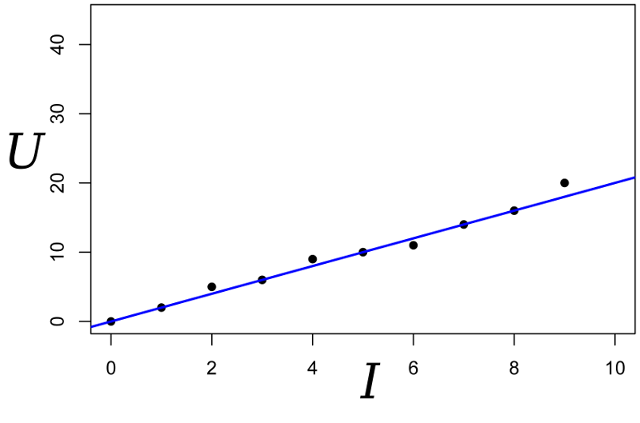
Escrevemos a expressão para a probabilidade do parâmetro R:
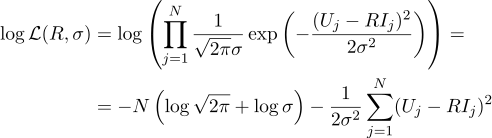
E, novamente, igualamos a zero a derivada parcial correspondente:
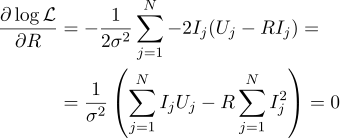
Então a resistência mais plausível R pode ser encontrada pela seguinte fórmula:
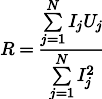
Esse resultado já é um pouco menos óbvio do que a média simples de todas as medições. Observe que, se fizermos cem medições na região de um ampère e uma na região de um quilo ampère, as cem medições anteriores praticamente não afetarão o resultado. Vamos lembrar deste fato, será útil para nós no próximo artigo.
Quarto Exemplo: Voltar para os Mínimos Quadrados
Certamente você já notou que, nos dois últimos exemplos, maximizar o logaritmo de probabilidade é equivalente a minimizar a soma dos quadrados do erro de estimativa. Vejamos outro exemplo. Faça a calibração da balança romana usando pesos de referência. Suponha que temos N cargas de referência de massa xj, pendure-as em uma balança e meça o comprimento da mola, obtemos N comprimentos de mola yj:

A lei de Hooke nos diz que a extensão da mola depende linearmente da força aplicada, e essa força inclui o peso das mercadorias e o peso da própria mola. Seja a rigidez da mola o parâmetro
a , mas a tensão da mola sob seu próprio peso é o parâmetro b. Então, podemos escrever a expressão da probabilidade de nossas medidas desta maneira (como antes, sob a hipótese do ruído de medição gaussiano):
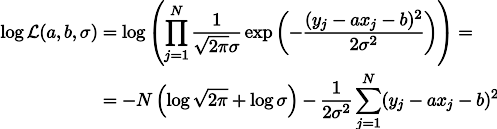
A maximização da probabilidade de L é equivalente a minimizar a soma dos quadrados dos erros de estimativa, ou seja, podemos procurar o mínimo da função S definida da seguinte forma:
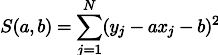
Em outras palavras, estamos procurando uma linha reta que minimize a soma dos quadrados dos comprimentos dos segmentos verdes:
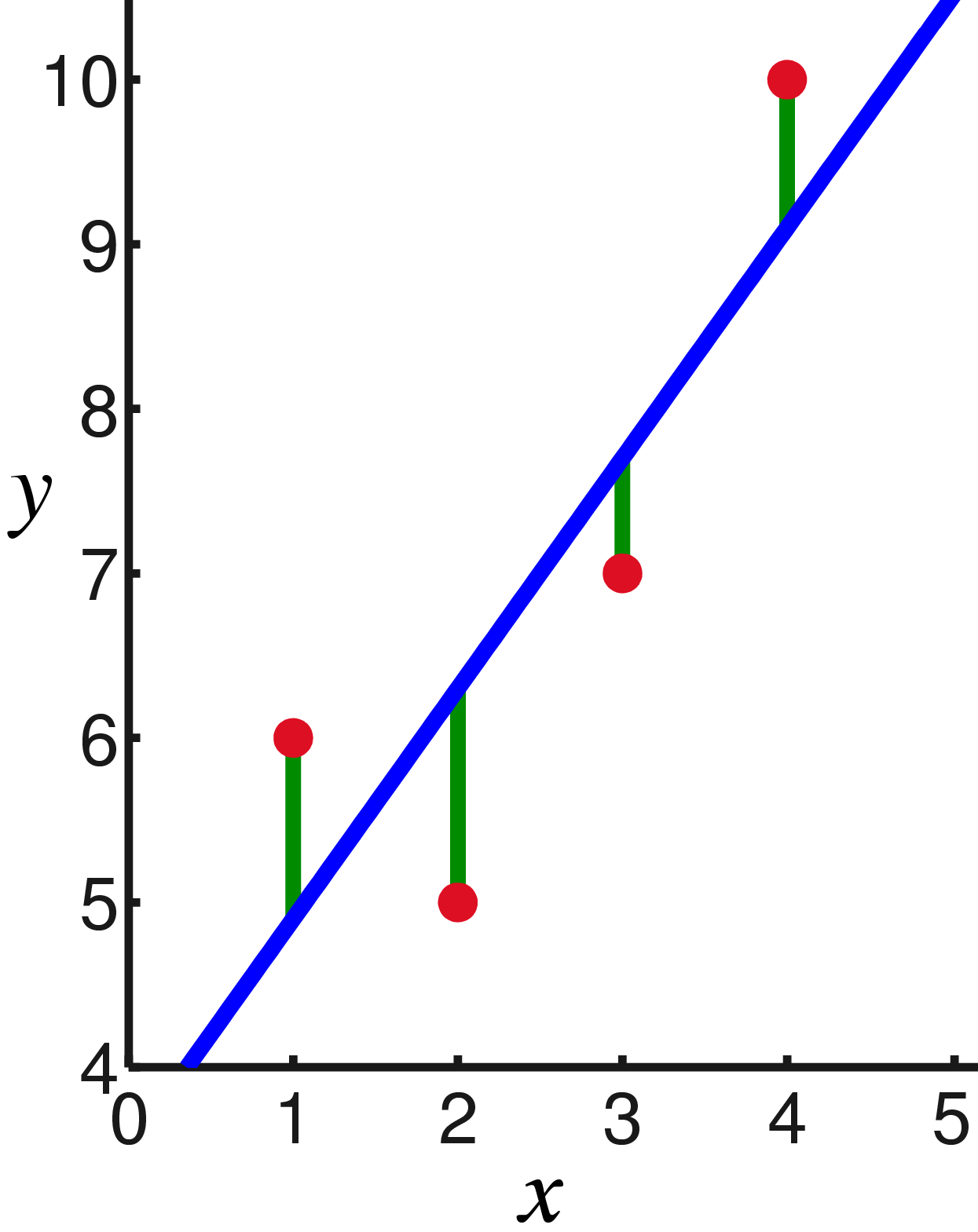
Bem, então, sem surpresas, definimos derivadas parciais para zero:
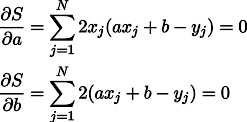
Temos um sistema de duas equações lineares com duas incógnitas:
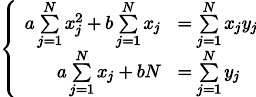
Recordamos a sétima série da escola e escrevemos a solução:

Conclusão
Métodos de mínimos quadrados são um caso especial de maximização de probabilidade para aqueles casos em que a densidade de probabilidade é gaussiana. No caso em que a densidade é (de maneira alguma) gaussiana, os mínimos quadrados fornecem uma estimativa que difere da MLE (estimativa máxima de similaridade). By the way, ao mesmo tempo, Gauss hipótese de que a distribuição não desempenha um papel, apenas a independência dos testes é importante.
Como você pode ver neste artigo, quanto mais longe na floresta, mais pesadas são as soluções analíticas para esse problema. Bem, sim, não estamos no século XVIII, temos computadores! Da próxima vez, veremos uma abordagem geométrica e, em seguida, programática para o problema do OLS, permanecer na linha.