Eu me preparei por um longo tempo e coletei material, espero que desta vez tenha ficado melhor. Dedico este artigo aos métodos básicos para resolver problemas de otimização matemática com limitações. Portanto, se você ouviu que o método simplex é um método
muito importante , mas ainda não sabe o que faz, esse artigo provavelmente o ajudará.
PS O artigo contém fórmulas matemáticas adicionadas pelo editor de macro. Eles dizem que às vezes não são exibidos. Existem também muitas animações em formato gif.
Preâmbulo
O problema da otimização matemática é um problema da forma “Localizar no conjunto
mathcalK o elemento
x∗ tal que para todos
x de
mathcalK realizado
f(x∗) leqf(x) ", Que na literatura científica provavelmente será escrito algo como isto
\ begin {array} {rl} \ mbox {minimiza} & f (x) \\ \ mbox {fornecido} & x \ in \ mathcal {K}. \ end {array}
\ begin {array} {rl} \ mbox {minimiza} & f (x) \\ \ mbox {fornecido} & x \ in \ mathcal {K}. \ end {array}
Historicamente, métodos populares, como descida por gradiente ou método de Newton, funcionam apenas em espaços lineares (e de preferência simples, por exemplo
mathbbRn ) Na prática, geralmente há problemas em que você precisa encontrar um mínimo, não no espaço linear. Por exemplo, você precisa encontrar o mínimo de alguma função nesses vetores
x=(x1, ldots,xn) para qual
xi geq0 , isso pode ser devido ao fato de que
xi denotar os comprimentos de qualquer objeto. Ou, por exemplo, se
x representam as coordenadas de um ponto que não deve exceder
r de
y isto é
|x−y | leqr . Para esses problemas, a descida do gradiente ou o método de Newton não é mais diretamente aplicável. Descobriu-se que uma classe muito grande de problemas de otimização é convenientemente coberta por "restrições", semelhantes às que descrevi acima. Em outras palavras, é conveniente representar o conjunto
mathcalK sob a forma de um sistema de igualdade e desigualdade
beginarraylgi(x) leq0, 1 leqi leqm,hi(x)=0, 1 leqi leqk. endarray
Problemas de minimização em um espaço do formulário
mathbbRn assim, começaram a chamá-los arbitrariamente de "problema irrestrito" e problemas sobre conjuntos definidos por conjuntos de igualdades e desigualdades - "problemas restritos".
Tecnicamente, absolutamente qualquer multidão
mathcalK pode ser representado como uma única igualdade ou desigualdade usando a função de
indicador , que é definida como
I_ \ mathcal {K} (x) = \ begin {cases} 0, & x \ notin \ mathcal {K} \\ 1, e x \ in \ mathcal {K}, \ end {cases}
no entanto, essa função não possui várias propriedades úteis (convexidade, diferenciabilidade etc.). No entanto, muitas vezes podemos imaginar
mathcalK na forma de várias igualdades e desigualdades, cada uma das quais possui essas propriedades. A teoria básica é resumida no caso
\ begin {array} {rl} \ mbox {minimiza} & f (x) \\ \ mbox {fornecido} & g_i (x) \ leq 0, ~ 1 \ leq i \ leq m \\ & Ax = b , \ end {array}
onde
f,gi - funções convexas (mas não necessariamente diferenciáveis),
A - matriz. Para demonstrar como os métodos funcionam, usarei dois exemplos:
- Tarefa de programação linear
$$ display $$ \ begin {array} {rl} \ mbox {minimize} & -2 & x ~~~ - & y \\ \ mbox {fornecido} & -1,0 & ~ x -0,1 & ~ y \ leq -1,0 \ \ & -1.0 & ~ x + ~ 0.6 & ~ y \ leq -1.0 \\ & -0.2 & ~ x + ~ 1.5 & ~ y \ leq -0.2 \\ & ~ 0.7 & ~ x + ~ 0.7 & ~ y \ Se a resposta ajudou de alguma forma, por favor, marque como resposta, caso a sua dúvida não tenha sido solucionada, por favor, poste novamente. 1.0 \\ \ end {array} $$ display $$
Em essência, esse problema consiste em encontrar o ponto mais distante do polígono na direção (2, 1), a solução para o problema é o ponto (4.7, 3.5) - o mais "correto" no polígono). Mas o próprio polígono
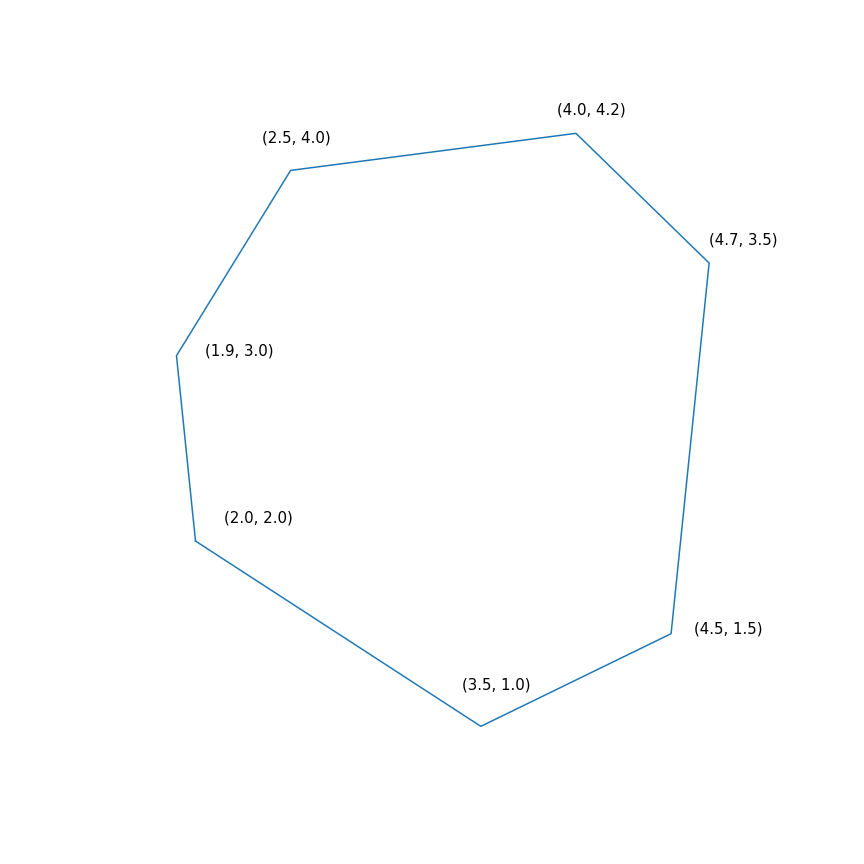
- Minimização de uma função quadrática com uma restrição quadrática
\ begin {array} {rl} \ mbox {minimize} e 0,7 (x - y) ^ 2 + 0,1 (x + y) ^ 2 \\ \ mbox {fornecido} & (x-4) ^ 2 + ( y-6) ^ 2 \ leq 9 \ end {array}
Método simplex
De todos os métodos que abordo com esta revisão, o método simplex é provavelmente o mais famoso. O método foi desenvolvido especificamente para programação linear e o único dos apresentados alcança a solução exata em um número finito de etapas (desde que a aritmética exata seja usada para cálculos, na prática isso geralmente não é assim, mas na teoria é possível). A ideia de um método simplex consiste em duas partes:
- Sistemas de desigualdades e igualdades lineares definem poliedros convexos multidimensionais (políttopos). No caso unidimensional, este é um ponto, raio ou segmento; no caso bidimensional, um polígono convexo; no caso tridimensional, um poliedro convexo. Minimizar a função linear é essencialmente encontrar o ponto "mais distante" em uma determinada direção. Penso que a intuição deve sugerir que esse ponto mais distante seja um certo pico, e é esse mesmo. Em geral, para um sistema de m desigualdades em n tridimensional um vértice é um ponto que satisfaz um sistema para o qual exatamente n dessas desigualdades se transformam em igualdade (desde que entre as desigualdades não haja equivalentes). Sempre há um número finito de tais pontos, embora possa haver muitos deles.
- Agora, temos um conjunto finito de pontos, de um modo geral, você pode simplesmente selecioná-los e ordená-los, ou seja, fazer algo assim: para cada subconjunto de n desigualdades, resolva o sistema de equações lineares compiladas nas desigualdades escolhidas, verifique se a solução se encaixa no sistema original de desigualdades e compare com outros pontos. Este é um método bastante simples, ineficiente, mas funcional. O método simplex, em vez de iterar, move-se de cima para cima ao longo das arestas, para que os valores da função objetivo melhorem. Acontece que, se um vértice não possui "vizinhos" nos quais os valores da função são melhores, é ideal.
O método simplex é iterativo, ou seja, melhora sequencialmente ligeiramente a solução. Para tais métodos, você precisa começar em algum lugar, no caso geral, isso é feito através da resolução de um problema auxiliar
\ begin {array} {rl} \ mbox {minimiza} & s \\ \ mbox {fornecido} & g_i (x) \ leq s, ~ 1 \ leq i \ leq m \\ \ end {array}
Se para resolver este problema
x∗,s∗ tal que
s∗ leq0 então executado
gi(x∗) leqs leq0 caso contrário, o problema original é geralmente fornecido em um conjunto vazio. Para resolver o problema auxiliar, você também pode usar o método simplex, mas o ponto de partida pode ser tomado
s= maxigi(x) com arbitrário
x . Encontrar o ponto de partida pode ser arbitrariamente chamado de primeira fase do método, encontrar a solução para o problema original pode ser arbitrariamente chamado de segunda fase do método.
A trajetória do método simplex de duas fasesA trajetória foi gerada usando scipy.optimize.linprog.
Descida Projetiva Gradiente
Sobre a descida do gradiente, escrevi recentemente um
artigo separado, no qual também descrevi brevemente esse método. Agora, esse método é bastante animado, mas está sendo estudado como parte de uma
descida mais geral do
gradiente proximal . A própria idéia do método é bastante banal: se aplicarmos descida gradiente a uma função convexa
f , com a escolha correta dos parâmetros, obtemos um mínimo global
f . Se, após cada passo da descida do gradiente, o ponto obtido for corrigido, levando sua projeção para um conjunto convexo fechado
mathcalK , como resultado, obtemos o mínimo da função
f em
mathcalK . Bem, ou mais formalmente, a descida de gradiente projetiva é um algoritmo que calcula sequencialmente
begincasesxk+1=yk− alphak nablaf(yk)yk+1=P mathcalK(xk+1), endcases
onde
P mathcalK(x)= mboxargminy in mathcalK |x−y |.
A última igualdade define o operador padrão de projeção no conjunto; de fato, é uma função que, de acordo com o ponto
x calcula o ponto mais próximo do conjunto
mathcalK . O papel da distância desempenha aqui
| ldots | , é importante notar que qualquer
norma pode ser usada aqui, no entanto, projeções com normas diferentes podem diferir!
Na prática, a descida do gradiente projetivo é usada apenas em casos especiais. Seu principal problema é que o cálculo da projeção pode ser ainda mais difícil que o original e precisa ser calculado várias vezes. O caso mais comum para o qual é conveniente usar a descida de gradiente projetiva são as "restrições de caixa", que têm a forma
elli leqxi leqri, 1 leqi leqn.
Nesse caso, a projeção é calculada com muita simplicidade, para cada coordenada
[P _ {\ mathcal {K}} (x)] _ i = \ begin {cases} r_i, & x_i> r_i \\ \ ell_i, & x_i <\ ell_i \\ x_i, e x_i \ em [\ ell_i, r_i ] \ end {cases}
O uso da descida do gradiente projetivo para problemas de programação linear é completamente sem sentido; no entanto, se você fizer isso, será algo parecido com isto
Trajetória de descida de gradiente projetiva para um problema de programação linear E aqui está a trajetória da descida do gradiente projetivo para o segundo problema, se
escolha tamanho de passo grande e se
escolha um tamanho pequeno passo Método elipsóide
Este método é digno de nota por ser o primeiro algoritmo polinomial para problemas de programação linear, podendo ser considerado uma generalização multidimensional do
método de bissecção . Vou começar com um
método mais geral
de separar o hiperplano :
- Em cada etapa do método, há um conjunto que contém a solução para o problema.
- Em cada etapa, um hiperplano é construído, após o qual todos os pontos situados em um lado do hiperplano selecionado são removidos do conjunto e alguns novos pontos podem ser adicionados a esse conjunto
Para problemas de otimização, a construção do "hiperplano de separação" é baseada na seguinte desigualdade para funções convexas
f(y) geqf(x)+ nablaf(x)T(y−x).
Se consertar
x , então para uma função convexa
f meio espaço
nablaf(x)T(y−x) geq0 contém apenas pontos com um valor não inferior a um ponto
x , o que significa que eles podem ser cortados, pois esses pontos não são melhores do que o que já encontramos. Para problemas com restrições, você também pode se livrar dos pontos que violam uma das restrições.
A versão mais simples do método de hiperplano de separação é simplesmente cortar meios espaços sem adicionar pontos. Como resultado, a cada passo, teremos um certo poliedro. O problema com esse método é que o número de faces do poliedro provavelmente aumentará de uma etapa para outra. Além disso, pode crescer exponencialmente.
O método elipsóide realmente armazena um elipsóide em cada etapa. Mais precisamente, após a construção do hiperplano, é construído um elipsóide de volume mínimo, que contém uma das partes do original. Isso pode ser alcançado adicionando novos pontos. Um elipsóide sempre pode ser definido por uma matriz definida positiva e um vetor (centro de um elipsóide) da seguinte maneira
\ mathcal {E} (P, x) = \ {z ~ | ~ (z-x) ^ TP (z-x) \ leq 1 \}.
A construção de um elipsóide mínimo em volume, contendo a interseção de meio espaço e outro elipsóide, pode ser feita usando
fórmulas moderadamente pesadas . Infelizmente, na prática, esse método ainda era tão bom quanto o método simplex ou o método de ponto interno.
Mas, na verdade, como funciona para
e para
Método do ponto interno
Esse método tem uma longa história de desenvolvimento, um dos primeiros pré-requisitos apareceu na mesma época em que o método simplex foi desenvolvido. Mas naquela época ainda não era eficaz o suficiente para ser usado na prática. Mais tarde, em 1984, uma
variante do método foi desenvolvida especificamente para programação linear, o que era bom tanto na teoria quanto na prática. Além disso, o método do ponto interno não se limita apenas à programação linear, diferentemente do método simplex, e agora é o principal algoritmo para problemas de otimização convexos com restrições.
A idéia básica do método é substituir as restrições por uma multa na forma da chamada
função de barreira . Função
F:Int mathcalK rightarrow mathbbR chamada de
função de barreira para o conjunto
mathcalK se
F(x) rightarrow+ infty mboxatx rightarrow parcial mathcalK.
Aqui
Int mathcalK - dentro
mathcalK ,
parcial mathcalK - fronteira
mathcalK . Em vez do problema original, propõe-se resolver o problema
mboxminimizarporx varphi(x,t)=tf(x)+F(x).
F e
varphi dada apenas no interior
mathcalK (de fato, é daí que o nome vem), a propriedade da barreira garante que
varphi pelo menos
x existe. Além disso, quanto mais
t quanto maior o impacto
f . Sob condições razoavelmente razoáveis, você pode conseguir isso se pretender
t ao infinito, em seguida, o mínimo
varphi convergirá para a solução do problema original.
Se o conjunto
mathcalK dado como um conjunto de desigualdades
gi(x) leq0, 1 leqi leqm então a escolha padrão da função de barreira é a
barreira logarítmicaF(x)=− summi=1 ln(−gi(x)).
Pontos mínimos
x∗(t) as funções
varphi(x,t) para diferentes
t forma uma curva, que geralmente é chamada de
caminho central , o método do ponto interno, por assim dizer, está tentando seguir esse caminho. É assim que parece
Exemplos de programação linear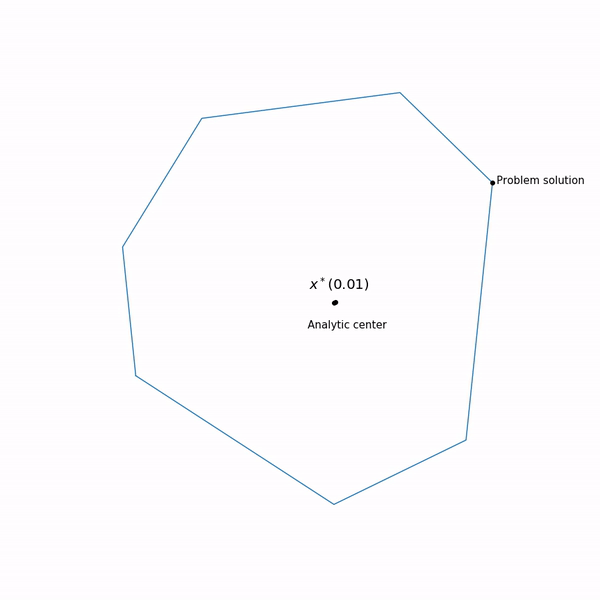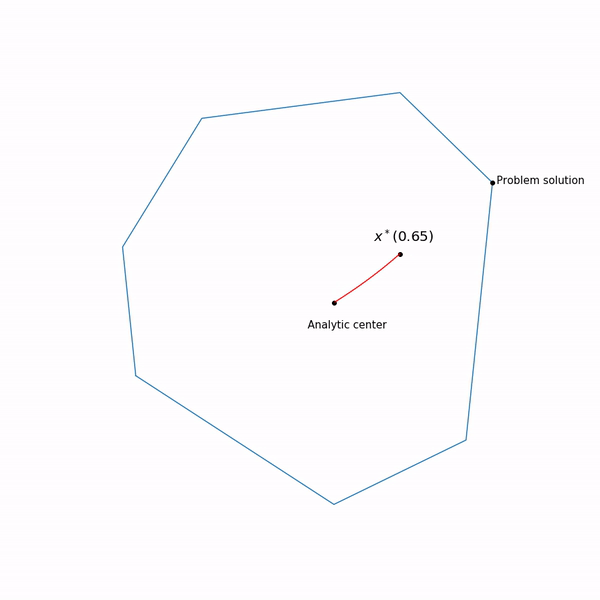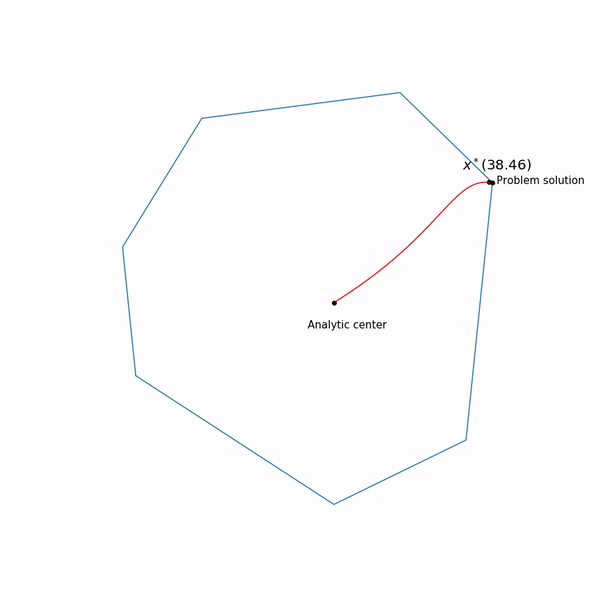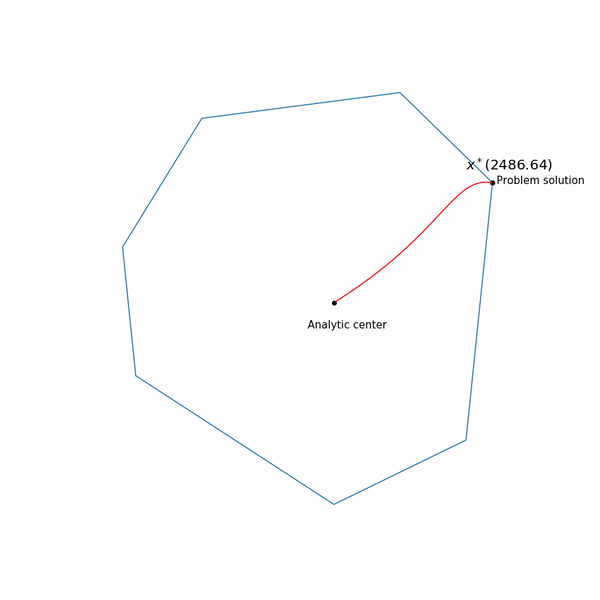 O centro analítico
O centro analítico é apenas
x∗(0) Finalmente, o próprio método de ponto interno tem a seguinte forma
- Selecione uma aproximação inicial x0 , t0>0
- Escolha uma nova aproximação usando o método Newton
xk+1=xk−[ nabla2x varphi(xk,tk)]−1 nablax varphi(xk,tk)
- Clique para ampliar t
tk+1= alphatk, alpha>1
O uso do método Newton é muito importante aqui: o fato é que, com a escolha certa da função barreira, a etapa do método Newton gera um ponto
que permanece dentro do nosso conjunto , experimentamos, nem sempre é emitido dessa forma. E, finalmente, é assim que a trajetória do método do ponto interno se parece
Tarefa de programação linearO ponto preto saltitante é
x∗(tk) , ou seja, ponto para o qual estamos tentando abordar a etapa do método de Newton na etapa atual.
Problema de programação quadrática