Em 2018, realizamos três concursos Yandex.Blitz - em aprendizado de máquina, desenvolvimento móvel e front-end. A terceira competição foi realizada recentemente - parabéns aos vencedores! Enquanto isso, queremos voltar para o segundo deles, onde tarefas foram propostas na junção de algoritmos e software de escrita para Android / iOS. Os candidatos ao cargo de desenvolvedor móvel na Yandex se beneficiarão da experiência na solução desses problemas. Leia a análise detalhada de alguns deles. E se você não participou do Blitz, é melhor primeiro tentar resolvê-los .

A tarefa do "suprimento de gás"
| Entrar | Conclusão | Prazo | Limite de memória |
|---|
| entrada padrão ou input.txt | saída padrão ou output.txt | 15 segundos | 15 megabytes |
A Nika está desenvolvendo um aplicativo para os principais gerentes de uma grande empresa de gás para ajudá-los a planejar a produção.
A empresa está considerando n campos que estão a 1 d d ... d d km de distância do oleoduto e podem produzir unidades de gás v 1 ... v i ... v n . Uma licença separada é vendida para cada campo - as licenças são s 1 ... s i ... s n .
Para conectar os campos à rodovia, você precisa construir gasodutos. Um empreiteiro que pode instalar m diferentes tipos de tubos ajuda essa empresa. Os tubos diferem entre si em comprimento (l 1 ... l i ... l m ) e preço (p 1 ... p i ... p m ). Eles podem ser combinados um com o outro como você quiser.
A empresa possui k moedas e deseja obter o máximo de gás possível.
Quanto a empresa será capaz de produzir se der ótimos pedidos ao contratado?
O pipeline pode ser maior que a distância do campo ao pipeline.
A primeira linha contém um número inteiro k ≤ 10 5 .
A segunda linha contém um número inteiro n ≤ 15.
As próximas n linhas contêm três números inteiros d i ≤ 100, v i ≤ 100 e s i ≤ 100.
Os números são separados por um espaço.
A próxima linha contém um número inteiro m ≤ 15.
As próximas m linhas contêm dois números inteiros l i ≤ 100 ep p ≤ 100. Os números são separados por um espaço.
A única linha com a resposta.
Exemplos
| Entrar | Conclusão |
116
3
58 7 50
81 71 56
52 57 31
3
47 9
1 25
18 61 | 57 |
Análise
Para começar, vamos definir a notação. Haja uma classe de objetos Depósito (depósito) com parâmetros $ inline $ Dd_ {i} $ inline $ (afastamento) $ inline $ Dv_ {i} $ inline $ (volume de produção) e $ inline $ Ds_ {i} $ inline $ (custo da licença). Objetos de índice desse tipo serão a variável i. Há também uma classe de objeto Pipeliner com parâmetros $ inline $ PPl_ {j} $ inline $ (o comprimento do tubo que o contratado pode construir) e $ inline $ PPp_ {j} $ inline $ (preço desse canal), indexe através de j. Os participantes da blitz muitas vezes perguntaram se um tipo de tubo pode ser usado duas vezes. Supõe-se que não, e este exemplo mostra claramente. Portanto, pelos termos desta tarefa, aceitar $ inline $ D_ {i} = {0, 1} $ inline $ (escolha um campo ou não) e $ inline $ PP_ {j} = {0, 1} $ inline $ (escolha ou não um contratado), você pode executar uma tarefa de programação linear:
$ inline $ \ sum \ limits_ {i} D_ {i} * Dv_ {i} \ rightarrow max \\ \ sum \ limits_ {i} D_ {i} * Ds_ {i} + \ sum \ limits_ {j} PP_ { j} * PPp_ {j} \ leq k \\ \ sum \ limits_ {i} D_ {i} * Dd_ {i} \ leq \ sum \ limits_ {j} PP_ {j} * PPl_ {j} \\ D_ { i} = {0, 1}, PP_ {j} = {0, 1} $ inline $
Pode ser resolvido, por exemplo, pelo método simplex. No entanto, pelos termos da tarefa, somos obrigados a retornar apenas o volume máximo de produção (ou seja, o valor da função objetivo) e não é necessário indicar quais campos e quais contratados devem ser selecionados. Juntamente com as restrições na condição, o problema pode ser resolvido pelo método de programação dinâmica, construindo uma tabela dp [length] [money], em que length é o comprimento do pipeline, dinheiro é dinheiro. Após a construção correta da tabela, basta encontrar o valor máximo nela, que será a resposta. As restrições de memória da tarefa são suficientes para criar.
A tarefa de "Torres e IA"
| Entrar | Conclusão | Prazo | Limite de memória |
|---|
| entrada padrão ou input.txt | saída padrão ou output.txt | 1 segundo | 64 megabytes |
Artem está desenvolvendo inteligência artificial jogando um jogo competitivo para celular. As regras do jogo são simples.
Antes dos jogadores, existem n torres com uma altura de c 1 ... c i ... c n . Por sua vez, o jogador pode quebrar uma das torres para que várias torres menores sejam obtidas. Os jogadores têm medo de ficar confusos nas torres, então concordaram com uma limitação: após a separação, duas torres da mesma altura não devem ser obtidas. Por exemplo, uma torre com uma altura de 7 pode ser dividida em (1, 2, 4), mas não em (1, 3, 3). A altura é sempre um número inteiro.
Perde quem não tem torres que podem ser destruídas.
Artem tem um amigo muito inteligente que joga da melhor maneira - é com ele que a inteligência artificial de Artem luta. Para avaliar o trabalho da IA, Artyom precisa saber se o robô deve ganhar se ambos os jogadores agirem de maneira ideal. Ajude-o com isso.
O homem sempre anda primeiro. Ele jogará com jogos de IA.
A primeira linha contém um número inteiro k <500.
Isto é seguido por k blocos de duas linhas.
A primeira linha de cada bloco é um número inteiro 0 <n ≤ 50.
A segunda linha de cada bloco possui n números inteiros 0 <c i ≤ 50. Os números são separados por espaços.
k linhas, cada uma das quais contém verdadeiro ou falso, dependendo se uma pessoa vence o jogo.
Exemplos
| Entrar | Conclusão |
2
1
4
2
1 1 | falsa
falsa |
Análise
O jogo de torre proposto é um jogo final justo para dois jogadores nos quais é impossível desenhar.
Portanto, a vitória de um determinado jogador no jogo é determinada pelo estado do jogo e pela ordem dos movimentos dos dois jogadores. Para os leitores que estão familiarizados com a teoria dos jogos, é óbvio que qualquer um dos jogos iguais de dois jogadores é realmente equivalente ao jogo "ele", o que também significa o nosso jogo.
Aqui está uma breve descrição dele - um jogo ( link para a fonte - clique nele para uma revisão detalhada):
Existem várias pilhas, cada uma com várias pedras. Em um movimento, o jogador pode pegar qualquer número diferente de zero de pedras de qualquer pilha e jogá-las fora. Consequentemente, ocorre uma perda quando não há mais movimentos restantes, ou seja, todas as pilhas estão vazias.
Portanto, o estado do jogo "ele" é descrito exclusivamente por um conjunto não ordenado de números naturais. Em um movimento, é permitido reduzir estritamente qualquer um dos números (se, como resultado, o número se tornar zero, então ele será removido do conjunto).
A solução para o jogo nim é encontrar a soma xor a partir do tamanho das pilhas, e somente se essa soma for diferente de zero podemos afirmar claramente que estamos em um estado vencedor.
Além disso, o teorema de Sprag-Grandi vem em nosso auxílio, que afirma que o estado U de qualquer jogo igual de dois jogadores pode ser associado a um punhado de jogos dele do tamanho X. Assim que uma função que especifica o mapeamento dos estados do nosso jogo para ele é um jogo, a solução para o problema será reduzida para resolvê-lo - um jogo que já é conhecido.
Tarefa “Indicação de Rating”
| Entrar | Conclusão | Prazo | Limite de memória |
|---|
| entrada padrão ou input.txt | saída padrão ou output.txt | 1 segundo | 64 megabytes |
Galya está desenvolvendo um agregador de análises. Ela decidiu designar as classificações das instituições com a ajuda de estrelas de sete pontas.
O sistema de renderização de entrada recebe um retângulo de altura he largura w, cujo canto superior esquerdo está localizado no ponto (x, y). Uma estrela deve ser desenhada de acordo com as seguintes regras:
- O tamanho de uma estrela é determinado pela largura ou altura do retângulo - ou seja, menor. (Veja os desenhos.)
- Se uma das dimensões do retângulo for maior que a dimensão correspondente da estrela, a estrela deve ser centralizada nessa dimensão.
- A estrela está apontada para cima.
O sistema de renderização espera as coordenadas dos vértices da estrela a partir do código Gali. Ajude Gale a calculá-los.
Para construir uma estrela de sete pontas, Galya toma o contorno externo da figura obtida conectando os vértices de um heptágono regular a um. No sistema de coordenadas, o eixo X é direcionado da esquerda para a direita, o eixo Y de cima para baixo. O programa Gali não falha, recebendo valores incorretos de largura e altura como entrada.
Uma única linha contém números inteiros x, y, weh, separados por espaços.
Exemplo: a entrada 150 0 50 100 indica um retângulo com uma largura de 50 pontos, uma altura de 100 pontos e com o canto superior esquerdo no ponto (150, 0).
A única linha que contém 28 números separados por espaços é a coordenada dos vértices da estrela, começando do topo e depois no sentido horário. Os números devem ser arredondados para o número inteiro mais próximo. Veja um exemplo da saída e uma ilustração do problema antes de prosseguir com a solução.
Exemplo: a saída de três pontos (1, 2), (3, 4), (5, 6) deve ser assim: 1 2 3 4 5 6.
Exemplos
| Entrar | Conclusão |
0 0 100 100 | 50 1 65 21 90 21 85 45 100 64 78 75 72 99 50 88 28 99 22 75 0 64 15 45 10 21 35 21 |
Anotações
A precisão necessária é de 10 dígitos significativos.
Sistema de coordenadas: o eixo X é direcionado da esquerda para a direita, o eixo Y de cima para baixo:
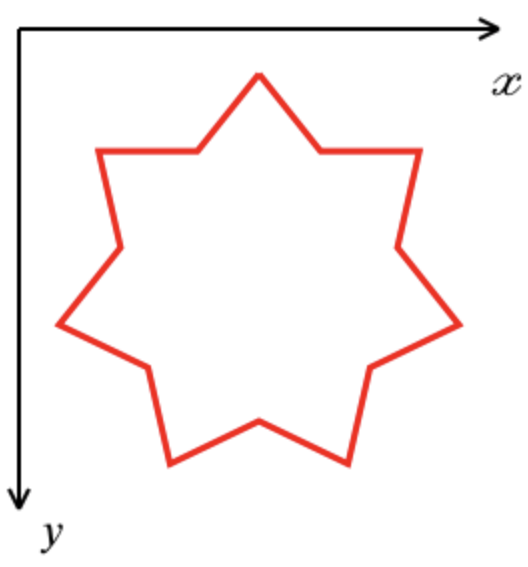
- Ordem esperada do vértice:
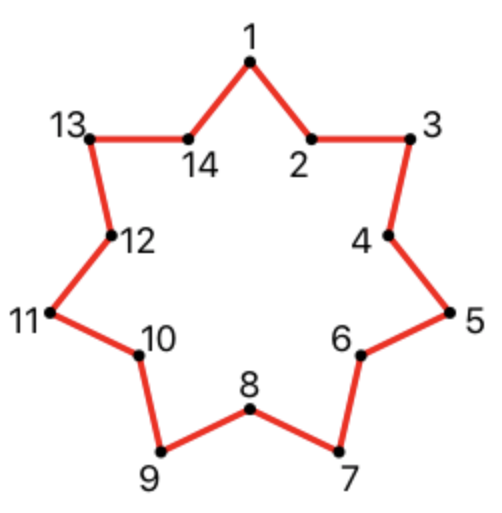
Exemplos de estrelas inscritas:
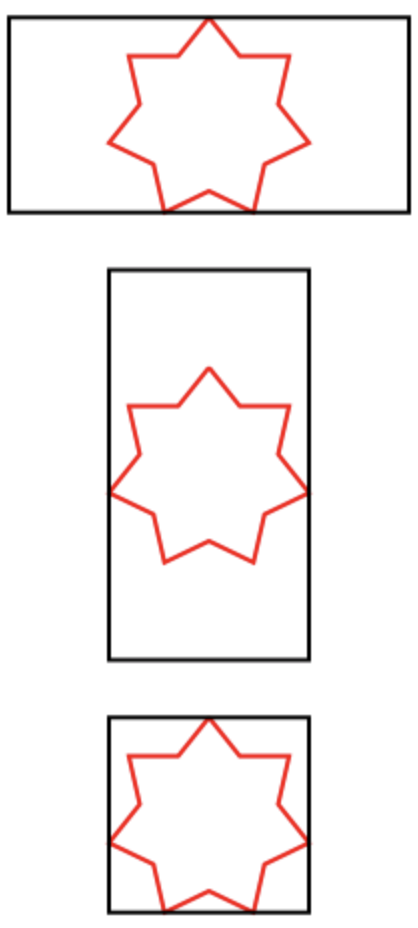
Análise
A solução para o problema é reduzida para três estágios: construir uma estrela de referência com a orientação desejada no espaço, escalar os pontos resultantes, calcular e aplicar o deslocamento.
Construindo uma estrela
A maneira mais fácil é construir uma estrela inscrita em um círculo com um raio unitário centrado na origem. Os pontos dos vértices externos são calculados usando trigonometria trivial, mas com os internos a tarefa é um pouco mais complicada. Eles podem ser encontrados em pelo menos duas maneiras. Uma maneira mais fácil é encontrar as interseções dos segmentos que conectam os vértices externos. Mais complicado é encontrar uma fórmula para calcular o raio de um círculo inscrito a partir do raio de um círculo circunscrito. A maneira mais fácil de fazer isso é primeiro, por exemplo, para uma estrela de 5 pontas e generalizada para a estrela de N pontas com um intervalo arbitrário entre os vértices conectados.
Dimensionamento
Em todos os casos, é dado o tamanho em que precisamos encaixar na estrela. Portanto, precisamos escalar os pontos obtidos para que a distância da esquerda para a direita não exceda a largura especificada e a distância da mais alta para a mais baixa não exceda a altura especificada. Tomamos os fatores de escala para trazer a largura e a altura aos valores desejados e selecionamos o menor. Como construímos prudentemente uma estrela de referência com o centro na origem, basta multiplicar as coordenadas de cada ponto pelo coeficiente selecionado.
Deslocamento
A última coisa que resta é mover nossos pontos para que a estrela fique dentro dos quadros dados. Os dados de entrada de todas as opções podem ser reduzidos para uma caixa delimitadora com uma determinada coordenada do canto superior esquerdo. Tudo é simples aqui: pegamos o ponto mais alto dos resultados obtidos na última etapa, consideramos a diferença de sua coordenada y com a coordenada y do canto superior esquerdo e mudamos todos os pontos verticalmente pelo valor obtido. Fazemos o mesmo com a coordenada x, basta pegar não o ponto mais alto, mas o ponto mais à esquerda. Há um toque final: centralize a estrela neste retângulo.
Outras ações dependem do coeficiente que escolhemos no estágio anterior:
- se escalado em altura - calculamos a diferença entre a largura do retângulo e a distância da esquerda ao ponto mais à direita;
- se tiverem escala em largura - calculamos a diferença entre a altura do retângulo e a distância do ponto mais alto ao mais baixo.
Divida o valor obtido por 2 e mude os pontos de acordo com a medida correspondente. Resposta recebida.
A tarefa "Rotação e escala de um círculo"
| Entrar | Conclusão | Prazo | Limite de memória |
|---|
| entrada padrão ou input.txt | saída padrão ou output.txt | 1 segundo | 64 megabytes |
A Vika está desenvolvendo um editor de gráficos para smartphones e tablets. Ela quer dar ao usuário a oportunidade de girar um círculo na tela com dois dedos e alterar seu tamanho, assim:
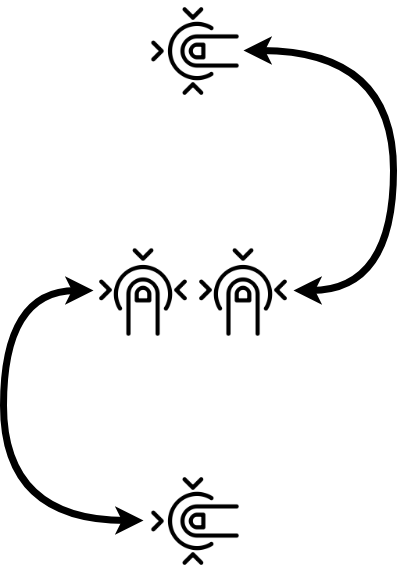
A figura gira no mesmo ângulo que o segmento que conecta os dedos. O tamanho da figura muda em proporção ao comprimento do segmento. Primeiro, a figura é girada e, em seguida, seu tamanho é alterado. Inicialmente, o círculo possui coordenadas (x, y) e raio r. É fornecida uma lista de eventos de toque que descrevem o gesto do usuário. Ajude o Vika a calcular as coordenadas finais do centro do círculo e seu raio. O círculo gira em relação ao ponto (a, b).
A descrição do evento de toque contém a identificação do dedo, coordenadas e tipo de evento. O primeiro dedo anexado pelo usuário recebe a identificação 0, a segunda - identificação 1 e assim por diante.
Um exemplo:
0 337 490 ACTION_DOWN - significa que, com o dedo 0 no ponto (337, 490), ocorreu o evento ACTION_DOWN.
Os eventos de toque são dos seguintes tipos:
- ACTION_DOWN - o usuário aplicou o primeiro dedo na tela em um determinado ponto.
- ACTION_POINTER_DOWN - o usuário aplicou um segundo dedo na tela em um determinado ponto.
- ACTION_MOVE - o usuário moveu o dedo para um determinado ponto.
- ACTION_POINTER_UP - o usuário moveu o segundo dedo para o ponto especificado e o soltou.
- ACTION_UP - o usuário moveu o primeiro dedo para o ponto especificado e o soltou.
- ACTION_CANCEL - gesto anulado pelo usuário.
A primeira linha contém os números x, ye er, separados por espaços. A segunda linha contém os números aeb separados por espaços. As próximas linhas contêm eventos de toque consecutivos.
A única linha com coordenadas e raio. Os números são separados por espaços.
Exemplo
| Entrar | Conclusão |
252 194 78
445.559
0 337.490 ACTION_DOWN
1.599.490 ACTION_POINTER_DOWN
1.576.564 ACTION_MOVE
1.552.590 ACTION_MOVE
0 407.375 ACTION_MOVE
1 505 615 ACTION_MOVE
1 482 620 ACTION_MOVE
0 477 360 ACTION_MOVE
1.435.616 ACTION_MOVE
1.411.607 ACTION_MOVE
0 547 386 ACTION_MOVE
1 364 548 ACTION_POINTER_UP
0 571 387 ACTION_UP | 831 704 73 |
Anotações
Ao exibir o resultado, é necessário arredondar todos os valores de ponto flutuante para um valor inteiro de acordo com as regras do arredondamento matemático.
Análise
Apesar de o gesto parecer complicado, ele pode ser dividido em dois componentes: rotação e escala. Para girar a figura, precisamos calcular o ângulo de rotação, que pode ser obtido usando a seguinte fórmula:
a = atan2 (prevTouchX2 - prevTouchX1, prevTouchY2 - prevTouchY1) - atan2 (currentTouchX2 - currentTouchX1, currentTouchY2 - currentTouchY1).
Após receber o ângulo de rotação, é necessário girar a própria figura, o que reduz a rotação de cada ponto da figura pelo ângulo de rotação. Depois de girarmos a figura, precisamos escalá-la. Escalar uma figura é bastante trivial. É necessário lembrar a distância entre o primeiro e o segundo dedo ao receber o evento ACTION_POINTER_DOWN para o segundo dedo. Depois disso, rastreando a distância entre os dois primeiros dedos, é possível calcular o coeficiente pelo qual você precisa dimensionar a figura.
A tarefa "Construção de estradas"
| Entrar | Conclusão | Prazo | Limite de memória |
|---|
| entrada padrão ou input.txt | saída padrão ou output.txt | 1 segundo | 64 megabytes |
Em um jogo para celular, o personagem principal constrói uma base em um planeta distante. Ele começa com as torres de perímetro conectadas por paredes diretas de laser. Os arquitetos da sede enviam a ele um plano mostrando n torres com coordenadas (x 1 , y 1 ) ... (x i , y i ) ... (x n , y n ). Do ponto de vista da defesa da base, não faz sentido colocar três ou mais torres vizinhas em uma linha reta. Os arquitetos da equipe, no entanto, às vezes posicionam as torres dessa maneira, de modo que o próprio jogador precisa remover as torres intermediárias extras.
Tendo terminado o perímetro, o herói começa a equipar a base por dentro. Ele quer construir k estradas entre as torres - a estrada pode conectar duas torres não adjacentes, mas não pode atravessar outra estrada ou muro. Quantas estradas você quiser pode sair de uma torre.
O herói tem p robôs de estrada. Para escolher o plano ideal de construção de estradas, o herói os instrui a classificar todas as opções possíveis. Os robôs começam a trabalhar simultaneamente e repetidamente trazem opções únicas para a localização das estradas. Se, antes da próxima iteração, houver menos opções do que robôs, os robôs extras serão liberados e enviados à cozinha para preparar o jantar. Os robôs restantes finalizam as últimas opções e desligam.
Se acontecer que você pode pavimentar a estrada fora da base, o herói declara a base insegura e voa para longe do planeta.
Quantos robôs trabalharão na cozinha?
A primeira linha contém três números inteiros 4 ≤ n ≤ 10 7 , 1 ≤ k ≤ n e um número primo 105 <p <11 × 104. Os números são separados por espaços.
As próximas n linhas contêm dois números inteiros 0 <x i , y i <109. Os números são separados por espaços.
A única linha com a resposta. Se a base não for segura, imprima -1.
Exemplo 1
| Entrar | Conclusão |
4 1 101363
0 0
1 0
1 1
0 1 | 101361 |
Existem duas maneiras de pavimentar a única estrada: (0, 0) - (1, 1) e (1, 0) - (0, 1). Dois robôs estarão envolvidos neles e o restante irá para a cozinha: p - 2 = 101 361.
Exemplo 2
| Entrar | Conclusão |
4 1 101363
1 0
2 0
0 1
1 2 | -1 |
Aqui você pode construir uma estrada entre (1, 0) - (0, 1), e isso fica fora da base. O herói reconhece a base como insegura, a resposta é -1.
Exemplo 3
| Entrar | Conclusão |
4 1 101363
0 0
1 0
2 0
0 1 | 101363 |
Torres (0, 0), (1, 0) e (2, 0) estão na mesma linha, então o herói não construirá a torre do meio (1, 0). Nenhuma estrada pode ser pavimentada, portanto, todos os robôs irão imediatamente para a cozinha: p = 101 363.
Análise
Dividimos a solução do problema em três etapas.
A primeira etapa é determinar para o conjunto de dados do vértice de entrada se o polígono é convexo e, em caso afirmativo, quantos vértices reais ele possui. Um polígono é convexo se todos os seus vértices estiverem localizados em um lado da linha que suporta qualquer aresta. Para cada triplo de vértices adjacentes $ inline $ (x_ {i-1}, y_ {i-1}), (x_ {i}, y_ {i}), (x_ {i + 1}, y_ {i + 1}) $ inline $ construa alguns vetores $ inline $ ab = ((x_ {i-1}, y_ {i-1}), (x_ {i}, y_ {i})) e bc = ((x_ {i}, y_ {i}), (x_ {i + 1}, y_ {i + 1})) $ inline $ e calcule o sinal da expressão ab.x bc.y - bc.x ab.y. Se a expressão for 0, os vértices ficam em uma linha reta e, de acordo com a condição do problema, a torre que fica no vértice do meio desaparece, reduzindo o número total de torres. Se para todos os triplos vértices o sinal do produto for 0 ou sempre o mesmo, vá para a segunda etapa, caso contrário, consideraremos a base insegura e imprimiremos a resposta -1.
Segundo passo. O número de maneiras de construir k diagonais disjuntas dentro de um N-gon convexo é $ inline $ V = 1 / (k + 1) {N-3 \ escolha k} {N + k-1 \ escolha k} $ inline $ , mas precisamos calcular a expressão p - V mod p, em que p é primo.
Imagine N! como $ inline $ a * p ^ e $ inline $ , onde o maior fator comum é a e p gcd (a, p) = 1.
$ inline $ {n \ escolhe r} = (n!) / (r! (nr)!) = a_ {1} * p ^ {e_ {1}} / a_ {2} * p ^ {e_ {2} } * a_ {3} * p ^ {e_ {3}} = (a_ {1} / a_ {2} * a_ {3}) * p ^ {e_ {1} -e_ {2} -e_ {3} } $ inline $
Se $ inline $ e_ {1} -e_ {2} -e_ {3}> 0 $ inline $ , a expressão é divisível por p e a resposta no problema é p.
Para o caso $ inline $ e_ {1} -e_ {2} -e_ {3}> 0 $ inline $ = 0 a resposta será $ inline $ a_ {1} / a_ {2} * a_ {3} $ inline $ mod p.
No cálculo, levamos em consideração que a b mod p = (a mod p) (b mod p) mod p e $ inline $ k ^ {- 1} $ inline $ mod p = $ inline $ (k) ^ {p-2} $ inline $ mod p para prime p.
Terceiro passo. Para calcular a expressão $ inline $ e_ {1} -e_ {2} -e_ {3} $ inline $ imagine n! como 1 2 ... p (p + 1) ... 2p (2p + 1) ..., enquanto (p + 1) ... (2p-1) mod p = 1 2 ... (p-1 ) = (p-1)! .. Total, n mod p = ( $ inline $ (p-1)! ^ k $ inline $ k (n mod p)!) mod p, onde k = piso (n / p).
Tarefa “Super Simple Scheduler”
| Entrar | Conclusão | Prazo | Limite de memória |
|---|
| entrada padrão ou input.txt | saída padrão ou output.txt | 10 segundos | 224 megabytes |
Não há tarefas a serem executadas no processador do smartphone. Sua implementação requer t 1 ... t i ... t unidades de tempo e, no início da d-ésima unidade de tempo, a i-ésima tarefa deve ser concluída.
Para chegar a tempo, as tarefas podem ser executadas em vários threads, no entanto, cada novo thread cria uma carga crescente na bateria. Na primeira corrente, uma unidade de energia é consumida por unidade de tempo, na segunda unidade e meia de energia, na terceira unidade e meia mais do que na segunda, etc.
As tarefas podem ser divididas em unidades de tempo: primeiro, conclua parcialmente uma, depois passe para outra e depois retorne à primeira. Você não pode executar diferentes partes de uma tarefa em diferentes segmentos ao mesmo tempo.
O planejador recebe tarefas uma de cada vez; Depois de receber uma tarefa, ele imediatamente aloca horários para ela. Depois que a tarefa é distribuída, o planejador não pode transferi-lo para outros slots.
Quanta energia será necessária para concluir todas as tarefas se elas forem distribuídas de maneira ideal?
A primeira linha contém o número inteiro 1 <n ≤ 3 × 10 3 .
As próximas n linhas contêm dois números inteiros 0 ≤ t i ≤ 10 4 e 0 ≤ d i ≤ 10 4 . Os números são separados por espaços.
A única linha com a resposta. Precisão - oito casas decimais.
Exemplo
| Entrar | Conclusão |
5
2 2
1 1
3 4
1 10
1 2 | 10.25000000 |
Análise
Como, de acordo com as condições do problema, basta calcular apenas a quantidade de energia consumida, podemos usar o método da solução calculando a quantidade de energia consumida para cada unidade de tempo. Ao planejar a tarefa, pegamos o valor mínimo da energia consumida k = 1 e, a partir do prazo final da tarefa, classificamos todos os intervalos do intervalo de tempo.
Se o consumo de energia do slot for menor que o coeficiente (k) e esse intervalo de tempo não foi usado no planejamento da tarefa, ocupamos esse slot para concluir a tarefa aumentando o coeficiente do slot em K. Quando atingimos o início do período, precisamos aumentar o coeficiente k em 1,5 vezes e repita a busca por horários, começando no prazo e até que a tarefa esteja completamente planejada. Após a conclusão do planejamento de todas as tarefas, resta apenas calcular o consumo total de energia adicionando os coeficientes obtidos de cada unidade de tempo.
A tarefa de objetos destrutíveis
| Entrar | Conclusão | Prazo | Limite de memória |
|---|
| entrada padrão ou input.txt | saída padrão ou output.txt | 2 segundos | 64 megabytes |
2D- . , : n- (x 1 , y 1 )...(x i , y i )...(x n , y n ). — , . . , — , .
, [0 1 2 3 4], 1 3 1 3, [1 2 3] [0 1 3 4].
, . . , , .
, ?
n ≤ 500. n x y. .
. — .
Exemplo 1
| Conclusão |
4
100 100
200 100
200 200
100 200 | 0.000000 |
Exemplo 2
| Conclusão |
6
167 84
421 84
283 192
433 298
164 275
320 133 | 326.986753 |
, , . « » : — . : , ( ) .
, ? ( , , ). : , , , . , , ( ) . even-odd rule: . — , ( ) , — .
, , — , . (, , ):
- ( );
- : , - ;
- ( , 10-5 );
- even-odd rule — ;
- : 180 .
«DNA»
| Conclusão | | |
|---|
| input.txt | output.txt | 8 | 128 |
, . , , . n . , . : A, T, G C. . .
n. n . . 6⋅10 6 .
. . . . . , .
( , ):
5
TTT
GAAGCT
CAAT
AGA
AGGCA
:
2 TTT
6 AGA
28 AGA
30 AGA
57 CAAT
86 AGA
100 GAAGCT
190 TTT
191 TTT
196 AGA
219 TTT
232 AGA
271 TTT
284 TTT
285 TTT
298 TTT
320 TTT
330 TTT
331 TTT
342 TTT
373 AGA
397 AGA
488 AGA
509 AGA
524 AGA
565 TTT
574 AGA
605 AGA
625 CAAT
630 AGA
681 CAAT
718 TTT
719 TTT
744 AGGCA
754 AGA
784 AGA
808 TTT
821 CAAT
833 AGA
861 CAAT
879 AGA
921 AGA
955 AGA
, . — , — . , . . , .
, .
«QR Quest»
| Conclusão | | |
|---|
| input.txt | output.txt | 1 | 64 |

t, . t n i , .
t , .
Exemplo 1
| Conclusão |
4
8 10 1 9 2 6 7 8
14 2 0 11 10 4 1 0
6 6 4 1 10 0 11 6
11 4 3 4 14 8 12 5 | 0 0
13
15
5 |
Exemplo 2
| Conclusão |
4
9 10 6 2 12 11 7 2
3 10 1 14 13 13 1 1
6 8 8 5 3 2 6 4
5 11 5 5 3 1 10 7 | 3
9
2
7 |
, . QR- , . - .
Um total de oito números foram inseridos - as coordenadas das células nessas tabelas, ou seja, 4 pares com as coordenadas da coluna e da linha. Era necessário adivinhar qual operação foi realizada com essas células e de qual tabela uma célula extra.
Usando manipulações simples, foi possível verificar que esse é o xoroma para quatro células das tabelas A, B e C, abordadas pelos índices a 0 ... a 7 :
R = A [a 0 , a 1 ] ^ B [a 2 , a 3 ] ^ B [a 4 , a 5 ] ^ C [a 6 , a 7 ].