Prova de locais onde não existem simetrias

Uma grande conquista matemática foi a hipótese de Zimmer encontrada por uma pequena equipe de pesquisadores.

Para grades em dimensões mais altas de simetria, nem sempre é possível transferir para dimensões abaixo da classificação

O sucesso de Robert Zimmer pode ser definido de várias maneiras. Como presidente da Universidade de Chicago desde 2006, ele chegou às manchetes, encontrando quantias de nove dígitos para financiar e publicar artigos em apoio à liberdade de expressão no campus. Mas antes de se tornar presidente da universidade, ele era matemático. E muito tempo depois que ele deixou uma pesquisa séria, o plano de pesquisa que ele lançou finalmente apresenta seus resultados.

Há um ano, três matemáticos provaram a hipótese de Zimmer relacionada a circunstâncias nas quais os espaços geométricos têm simetrias de um determinado tipo. Sua prova se tornou uma das maiores realizações matemáticas dos últimos anos. Põe fim à questão que surgiu diante de Zimmer durante sua intensa atividade mental no final da década de 1970 e no início da década de 1980.

"Eu diria que fui para a cama cinco anos com pensamentos sobre essa tarefa, todas as noites, então fiquei obcecado por ela, e é ótimo observar como as pessoas a resolveram", disse Zimmer.

Geralmente, quanto maior o espaço da dimensão geométrica, mais simetrias podem estar nele. Isso pode ser imaginado pelo estudo de um círculo existente em um plano bidimensional e de uma bola que se estende em três dimensões: existem mais maneiras de girar a bola do que maneiras de girar um círculo. Dimensões adicionais da esfera criam simetrias adicionais.

A conjectura de Zimmer refere-se a simetrias de um tipo especial, conhecidas como redes de alto escalão. Ela pergunta se a medida do espaço geométrico limita o uso de simetrias desse tipo. Os autores do novo trabalho - Aaron Brown e Sebastian Hurtado-Salazar, da Universidade de Chicago e David Fisher, da Universidade de Indiana - mostraram que, com o número de medições, menos de certas simetrias específicas não são observadas. Assim, eles provaram a exatidão da hipótese de Zimmer.


Robert Zimmer, agora presidente da Universidade de Chicago, desenvolveu uma hipótese com seu nome há quase 40 anos

Seu trabalho responde a uma pergunta importante e duradoura, abrindo novas maneiras de estudar muitas outras. Também revela as propriedades intrínsecas dos espaços geométricos. A simetria é uma das propriedades mais simples de tais espaços. O novo trabalho diz que simetrias podem existir em espaços de um tipo e não em outros. Essa conquista foi alcançada após décadas de inatividade.

"A hipótese parecia que poderia manter as pessoas ocupadas por muito tempo", disse Amy Wilkinson, matemática da Universidade de Chicago, que organizou a conferência deste ano sobre essa prova. "E eles simplesmente destruíram essa questão".

Simetrias satisfatórias

A simetria é um dos primeiros conceitos geométricos que as crianças encontram em matemática. Com as próprias mãos, eles aprendem que você pode girar, virar e mudar o formulário e, no final, obter o mesmo formulário com o qual eles começaram. Preservar a forma do objeto como resultado de mudanças responde com uma certa satisfação interna - essa é uma sugestão de uma ordem mais profunda no Universo.

Os matemáticos têm sua própria linguagem formal para estudar simetria. Isso lhes dá a oportunidade de discutir de forma concisa sobre várias simetrias aplicáveis ​​em um determinado espaço geométrico.

Um quadrado, por exemplo, possui oito simetrias - oito maneiras de girá-lo ou girá-lo, obtendo novamente o quadrado. O círculo pode ser girado qualquer número de graus; ela tem um número infinito de simetrias. Os matemáticos coletam todas as simetrias de um determinado objeto geométrico, ou espaço, e as agrupam em um "grupo".

Os grupos são interessantes por si só. Eles geralmente aparecem como resultado do estudo de certos espaços geométricos, mas às vezes aparecem em um contexto que não tem nenhuma relação com a geometria. Por exemplo, grupos podem formar conjuntos numéricos (por exemplo, existe uma certa simetria na adição de 5 ou subtração de 5 de um número).

"Um grupo, em princípio, pode aparecer como uma simetria de coisas completamente diferentes", disse Zimmer.

Existem formas de simetria mais exóticas do que aquelas que estudamos na escola. Considere, por exemplo, a simetria das redes. A rede mais simples é uma grade bidimensional. No plano, a treliça pode ser deslocada para cima, baixo, esquerda, direita por qualquer número de quadrados e obter uma treliça que se pareça exatamente igual à original. Você também pode refletir a grade através de qualquer número de células individuais. Os espaços com grades têm um número infinito de diferentes simetrias de grades.



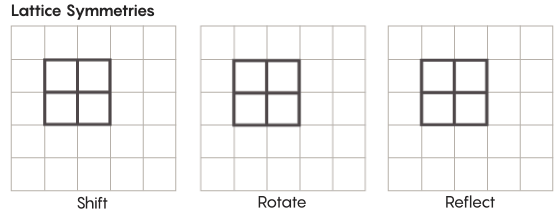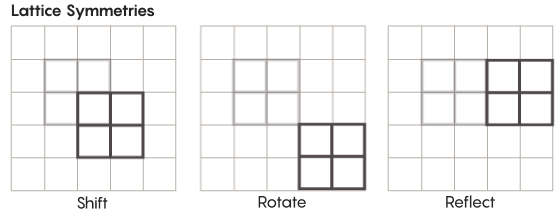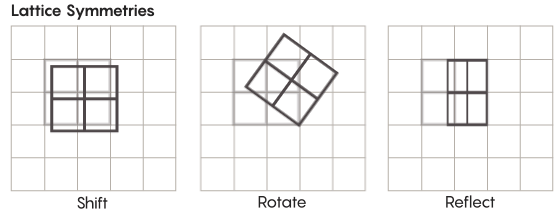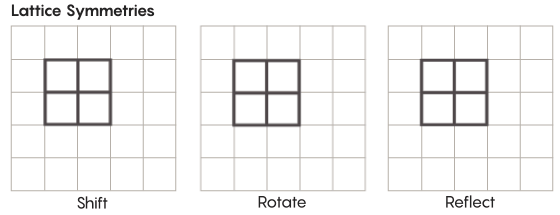
As redes podem existir em qualquer número de dimensões. No espaço tridimensional, uma treliça pode consistir em cubos, não quadrados. Em quatro ou mais dimensões, não será possível apresentar a rede, mas funciona da mesma maneira; matemáticos podem descrevê-lo exatamente. Grupos de interesse para a hipótese de Zimmer incluem redes de “classificação mais alta” ou redes em certos espaços de dimensões mais altas. "Essa estrutura estranha seria muito bonita, se pudesse ser vista, mesmo que não me fosse dada", disse Khurtado-Salazar. "Parece-me que olhá-la seria muito bom."

No século 20, os matemáticos descobriram esses grupos sob várias condições - não apenas na geometria, mas também na teoria dos números, lógica e ciência da computação. Ao abrir novos grupos, é lógico fazer a pergunta - que tipo de espaço possui esses conjuntos de simetrias?

Às vezes, os grupos são obviamente impossíveis de combinar com o espaço. Pode-se entender rapidamente que o grupo de simetrias de um círculo não pode ser aplicado a um quadrado. Gire o quadrado 10 graus e você não obterá o quadrado original. Mas uma mistura de um grupo com um número infinito de simetrias e espaço com muitas dimensões dificulta a determinação da aplicabilidade do grupo.

"Quando se muda para um grupo mais complexo em mais dimensões", disse Zimmer, "essas questões se tornam muito complicadas".

Conexão indireta

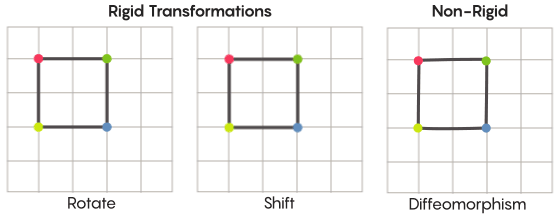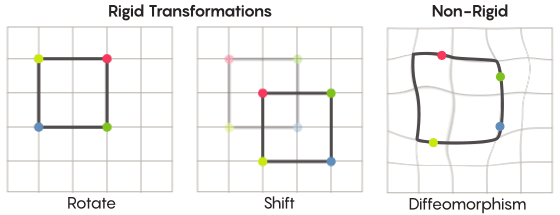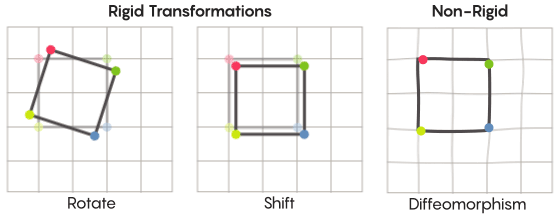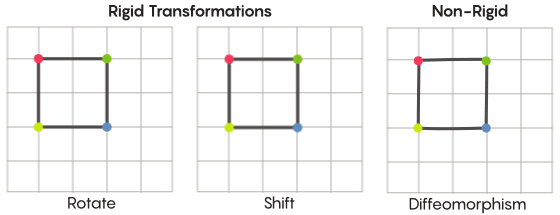
Imaginando simetria, imaginamos a rotação de toda a forma - por exemplo, um quadrado girado 90 graus. Mas em um nível básico, a simetria depende de pontos em movimento. A transformação simétrica do espaço significa que você precisa pegar todos os pontos dele e movê-lo para outro ponto. Nesse sentido, uma rotação de 90 graus do quadrado significa que você precisa pegar cada ponto do quadrado e girá-lo 90 graus para que não fique na aresta a partir da qual você começou.


David fisher

O problema dos pontos móveis pode ser resolvido mais ou menos estritamente. As transformações simétricas mais familiares - o reflexo de um quadrado em relação à diagonal ou sua rotação em 90 graus - são muito rigorosas. Rigoroso no sentido de que eles não confundem pontos. Os pontos que eram vértices antes da reflexão permanecem vértices depois (eles se tornam vértices diferentes) e os pontos que compunham as arestas retas, após a reflexão, ainda compõem as arestas retas (apenas diferentes).

Existem tipos menos rígidos e flexíveis de transformações simétricas e são interessantes no contexto da hipótese de Zimmer. Em tais transformações, os pontos mudam sua organização mais fortemente; eles não mantêm necessariamente suas conexões anteriores após a transformação. Por exemplo, você pode mover cada ponto do quadrado por três unidades de comprimento ao longo do perímetro do quadrado - isso satisfaz os requisitos básicos de uma transformação simétrica, ou seja, basta deslocar cada ponto no espaço para outro lugar. Aaron Brown, co-autor da prova, descreveu como essas transformações de forma mais livre podem parecer no contexto da bola.

“Você pode pegar os pólos norte e sul e torcer em direções opostas. Então a distância entre os pontos aumentará ”, disse Brown.

No caso de uma grade, em vez de simplesmente movê-la ao longo do plano, você pode dobrá-la, esticá-la em alguns lugares e apertá-la em outros, para que a malha transformada não se sobreponha mais à malha original. Tais transformações são menos rigorosas e são denominadas diffeomorfismos .



Zimmer tinha boas razões para usar essa versão menos rigorosa da simetria em sua hipótese. Malhas especiais do mais alto nível relacionadas a essa hipótese foram estudadas pela primeira vez na década de 1960 por Grigory Alexandrovich Margulis , que recebeu o Prêmio Fields por seu trabalho. Margulis fez uma descrição completa de que tipo de espaço pode ser transformado usando essas redes de classificação mais alta, se apenas transformações estritas forem permitidas.

A hipótese de Zimmer tornou-se uma continuação natural do trabalho de Margulis. Começa com uma lista de espaços nos quais as treliças de primeira linha podem funcionar - Margulis descobriu essa lista - e pergunta se essa lista está se expandindo, se é permitido que as treliças tenham transformações menos estritas.

No novo trabalho, três matemáticos provaram que o enfraquecimento da definição de simetria não altera o escopo das simetrias das redes de ordem superior. Mesmo que as redes tenham transformações muito irregulares - para deslocar, dobrar, esticar - as redes ainda terão uma restrição estrita no escopo.

“Depois de adicionar essa flexibilidade à declaração do problema, intuitivamente, é claro, parece que as grades podem atuar mais amplamente. Portanto, é surpreendente que, na realidade, a resposta seja "não" - em alguns casos, eles não podem ", disse Fisher.

Os matemáticos estabeleceram correspondências exatas entre a dimensão do espaço e a dimensão, ou posição, das redes, para redes que podem desempenhar o papel de simetria em um determinado espaço. Em geral, eles mostraram que quanto maior a classificação da rede, mais medidas são necessárias para o espaço que pode acomodá-la. Mesmo com considerável flexibilidade na transformação do espaço, as transformações de redes de alto escalão são limitadas a dimensões mais altas.

"Isso sugere que há algo muito fundamental na estrutura dos espaços, o que implica sua capacidade de acomodar essas transformações", disse Wilkinson.

A hipótese de Zimmer é apenas o primeiro passo para um programa maior. Tendo lidado com isso, os co-autores do trabalho impuseram uma restrição grosseira aos espaços em que redes de alto escalão podem ser transformadas. A próxima fase mais ambiciosa do trabalho será a concentração nos espaços em que as redes podem existir - e, em seguida, a classificação de todas as diferentes maneiras de transformar as redes desses espaços.

“No final, o programa deve ser capaz de classificar todos esses métodos. Existem muitas questões interessantes além do simples estabelecimento do fato da existência de certos lugares em que as grades não podem operar ”, disse Zimmer.