Julia e retratos de fase de sistemas dinâmicos

Continuamos a dominar a jovem e promissora linguagem de propósito geral Julia . Mas, para começar, precisamos apenas da possibilidade muito estreita de aplicação - para resolver problemas típicos da física. Esta é a tática mais conveniente para dominar o instrumento: para obter uma mão, resolveremos problemas prementes, aumentando gradualmente a complexidade e encontrando maneiras de facilitar nossa vida. Resumindo, resolveremos difusões e construiremos gráficos.

Para começar, baixe o pacote gráfico Gadfly e imediatamente a versão completa do desenvolvedor, para que funcione bem com a nossa Julia 1.0.1. Dirigimos em nosso notebook REPL, JUNO ou Jupyter:

using Pkg pkg"add Compose#master" pkg"add Gadfly#master" 

Não é a opção mais conveniente, mas enquanto aguarda a atualização do PlotlyJS , você pode tentar fazer uma comparação.

Você também precisa de uma ferramenta poderosa para resolver equações diferenciais .

 ]add DifferentialEquations #     

Este é o pacote mais extenso e suportado que oferece muitos métodos para solucionar diferenças. Agora vá para os retratos de fase.

Soluções de equações diferenciais ordinárias costumam ser mais convenientes para representar de forma incomum $$$y ^ 1 (t), ..., y ^ L (t)$, e no espaço de fase ao longo dos eixos em que os valores de cada uma das funções encontradas são plotados. Além disso, o argumento t é incluído nos gráficos apenas parametricamente. No caso de dois EDOs, esse gráfico - o retrato de fase do sistema - é uma curva no plano de fase e, portanto, é especialmente evidente.

Oscilador

Dinâmica do oscilador harmônico $$$\ gama$é descrito pelo seguinte sistema de equações:

e independentemente das condições iniciais (x0, y0), chega a um estado de equilíbrio, um ponto (0,0) com ângulo de deflexão zero e velocidade zero.

At $$$\ gama = 0$a solução assume a forma característica de um oscilador clássico.

 using DifferentialEquations, Gadfly #     -    function garmosc(ω = pi, γ = 0, x0 = 0.1, y0 = 0.1) A = [0 1 -ω^2 γ] syst(u,p,t) = A * u # ODE system u0 = [x0, y0] # start cond-ns tspan = (0.0, 4pi) # time period prob = ODEProblem(syst, u0, tspan) # problem to solve sol = solve(prob, RK4(),reltol=1e-6, timeseries_steps = 4) N = length(sol.u) J = length(sol.u[1]) U = zeros(N, J) for i in 1:N, j in 1:J U[i,j] = sol.u[i][j] #      end U end 

Vamos analisar o código. A função aceita os valores do parâmetro de frequência e atenuação, bem como as condições iniciais. A função syst () aninhada define o sistema. Para que isso acontecesse, eles usaram a multiplicação de matrizes de uma linha. A função resolve () , usando um grande número de parâmetros, é configurada com muita flexibilidade para solucionar o problema, mas apenas indicamos o método da solução - Runge-Kutta 4 ( existem muitos outros ), o erro relativo e o fato de que nem todos os pontos devem ser salvos, mas apenas a cada quarto . A matriz de resposta é armazenada na variável sol , além disso, sol.t contém um vetor de vezes e sol.u resolve o sistema nesses momentos. Tudo isso é desenhado com calma em Gráficos , e para o Gadfly você precisa completar a resposta em uma matriz mais conveniente. Como não precisamos de tempo, retornamos apenas soluções.

Vamos criar um retrato de fase:

 Ans0 = garmosc() plot(x = Ans0[:,1], y = Ans0[:,2]) 

Entre as funções de alta ordem, a broadcast(f, [1, 2, 3]) é especialmente notável para nós, que substitui alternadamente os valores da matriz [1, 2, 3] na função f . Gravação curta f.([1, 2, 3]) . Isso é útil para variar a frequência, o parâmetro de atenuação, a coordenada inicial e a velocidade inicial.

 L = Array{Any}(undef, 3)#     (  ) clr = ["red" "green" "yellow"] function ploter(Answ) for i = 1:3 L[i] = layer(x = Answ[i][:,1], y = Answ[i][:,2], Geom.path, Theme(default_color=clr[i]) ) end p = plot(L[1], L[2], L[3]) end Ans1 = garmosc.( [pi 2pi 3pi] )#  p1 = ploter(Ans1) Ans2 = garmosc.( pi, [0.1 0.3 0.5] )#  p2 = ploter(Ans2) Ans3 = garmosc.( pi, 0.1, [0.2 0.5 0.8] ) p3 = ploter(Ans3) Ans4 = garmosc.( pi, 0.1, 0.1, [0.2 0.5 0.8] ) p4 = ploter(Ans4) set_default_plot_size(16cm, 16cm) vstack( hstack(p1,p2), hstack(p3,p4) ) #     

Agora consideramos não pequenas oscilações, mas oscilações de amplitude arbitrária:

O diagrama de fases da solução não é uma elipse (que indica a não linearidade do oscilador). Quanto menos escolhermos a amplitude das oscilações (ou seja, as condições iniciais), menos não linearidade aparecerá (portanto, pequenas oscilações do pêndulo podem ser consideradas harmônicas).

 function ungarmosc(ω = pi, γ = 0, x0 = 0.1, y0 = 0.1) function syst(du,u,p,t) du[1] = u[2] du[2] = -sin( ω*u[1] )+γ*u[2] end u0 = [x0, y0] # start cond-ns tspan = (0.0, 2pi) # time period prob = ODEProblem(syst, u0, tspan) # problem to solve sol = solve(prob, RK4(),reltol=1e-6, timeseries_steps = 4) N = length(sol.u) J = length(sol.u[1]) U = zeros(N, J) for i in 1:N, j in 1:J U[i,j] = sol.u[i][j] #      end U end Ans1 = ungarmosc.( [pi 2pi 3pi] ) p1 = ploter(Ans1) Ans2 = ungarmosc.( pi, [0.1 0.4 0.7] ) p2 = ploter(Ans2) Ans3 = ungarmosc.( pi, 0.1, [0.1 0.5 0.9] ) p3 = ploter(Ans3) Ans4 = ungarmosc.( pi, 0.1, 0.1, [0.1 0.5 0.9] ) p4 = ploter(Ans4) vstack( hstack(p1,p2), hstack(p3,p4) ) 

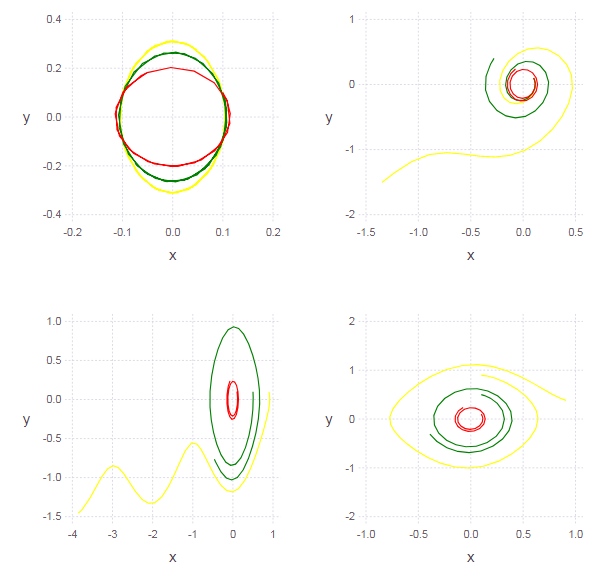
Brusselator

Este modelo descreve uma certa reação química autocatalítica na qual a difusão desempenha um papel. O modelo foi proposto em 1968 por Lefebvre e Prigozhin.

Funções desconhecidas $$$u_1 (t), \, u_2 (t)$refletem a dinâmica da concentração de produtos intermediários de uma reação química. Parâmetro do modelo $$$\ mu$a concentração inicial do catalisador (terceira substância) faz sentido.

Mais detalhadamente, a evolução do retrato de fase do Bruxelas pode ser observada através da realização de cálculos com vários parâmetros. $$$\ mu$. Com o aumento, o nó primeiro mudará gradualmente para um ponto com coordenadas (1, $$$\ mu$) até atingir um valor de bifurcação $$$\ mu$= 2. Nesse ponto, há uma reestruturação qualitativa do retrato, expressa no nascimento do ciclo limite. Com mais aumento $$$\ mu$apenas uma mudança quantitativa nos parâmetros deste ciclo ocorre.

 function brusselator(μ = 0.1, u0 = [0.1; 0.1]) function syst(du,u,p,t) du[1] = -(μ+1)*u[1] + u[1]*u[1]*u[2] + 1 du[2] = μ*u[1] - u[1]*u[1]*u[2] end tspan = (0.0, 10) # time period prob = ODEProblem(syst, u0, tspan) # problem to solve sol = solve(prob, RK4(),reltol=1e-6, timeseries_steps = 1) N = length(sol.u) J = length(sol.u[1]) U = zeros(N, J) for i in 1:N, j in 1:J U[i,j] = sol.u[i][j] #      end U end L = Array{Any}(undef, 10) function ploter(Answ) for i = 1:length(Answ) L[i] = layer(x = Answ[i][:,1], y = Answ[i][:,2], Geom.path ) end plot(L[1], L[2], L[3], L[4], L[5], L[6], L[7], L[8], L[9], L[10]) end SC = [ [0 0.5], [0 1.5], [2.5 0], [1.5 0], [0.5 1], [1 0], [1 1], [1.5 2], [0.1 0.1], [0.5 0.2] ] Ans1 = brusselator.( 0.1, SC ) Ans2 = brusselator.( 0.8, SC ) Ans3 = brusselator.( 1.6, SC ) Ans4 = brusselator.( 2.5, SC ) p1 = ploter(Ans1) p2 = ploter(Ans2) p3 = ploter(Ans3) p4 = ploter(Ans4) set_default_plot_size(16cm, 16cm) vstack( hstack(p1,p2), hstack(p3,p4) ) 

O suficiente por hoje. Da próxima vez, tentaremos aprender a usar outro pacote gráfico para novas tarefas, enquanto digitamos nossa mão na sintaxe de Julia. No processo de solução de problemas, lentamente começando a ser rastreado, não que os prós e os contras sejam diretos ... ao contrário, comodidades e inconvenientes - uma conversa separada deve ser dedicada a isso. E, é claro, eu gostaria de ver algo mais sério no meu habra do que nos meus jogos com funções - portanto, peço aos julistas que nos digam mais sobre projetos mais sérios, isso ajudaria muitos, e em particular, o aprendizado dessa linguagem maravilhosa.