🎬 🌫️ 🍘 Julia e equações diferenciais parciais 🧚 ⛎ 🤦🏾

No exemplo dos modelos físicos mais típicos, consolidaremos as habilidades de trabalhar com funções e nos familiarizaremos com o visualizador rápido, conveniente e bonito do PyPlot, que fornece todo o poder do Matplotlib Python. Haverá muitas fotos (escondidas sob os spoilers)

Garantimos que tudo esteja limpo e fresco sob o capô:

Sob o capô

]status Status `C:\Users\\.julia\environments\v1.0\Project.toml` [537997a7] AbstractPlotting v0.9.0 [ad839575] Blink v0.8.1 [159f3aea] Cairo v0.5.6 [5ae59095] Colors v0.9.5 [8f4d0f93] Conda v1.1.1 [0c46a032] DifferentialEquations v5.3.1 [a1bb12fb] Electron v0.3.0 [5789e2e9] FileIO v1.0.2 [5752ebe1] GMT v0.5.0 [28b8d3ca] GR v0.35.0 [c91e804a] Gadfly v1.0.0+ #master (https://github.com/GiovineItalia/Gadfly.jl.git) [4c0ca9eb] Gtk v0.16.4 [a1b4810d] Hexagons v0.2.0 [7073ff75] IJulia v1.13.0+ [`C:\Users\\.julia\dev\IJulia`] [6218d12a] ImageMagick v0.7.1 [c601a237] Interact v0.9.0 [b964fa9f] LaTeXStrings v1.0.3 [ee78f7c6] Makie v0.9.0+ #master (https://github.com/JuliaPlots/Makie.jl.git) [7269a6da] MeshIO v0.3.1 [47be7bcc] ORCA v0.2.0 [58dd65bb] Plotly v0.2.0 [f0f68f2c] PlotlyJS v0.12.0+ #master (https://github.com/sglyon/PlotlyJS.jl.git) [91a5bcdd] Plots v0.21.0 [438e738f] PyCall v1.18.5 [d330b81b] PyPlot v2.6.3 [c4c386cf] Rsvg v0.2.2 [60ddc479] StatPlots v0.8.1 [b8865327] UnicodePlots v0.3.1 [0f1e0344] WebIO v0.4.2 [c2297ded] ZMQ v1.0.0

Caso contrário, teremos tudo o que precisamos hoje

 julia>] pkg> add PyCall pkg> add LaTeXStrings pkg> add PyPlot pkg> build PyPlot #     build #    -      ,    pkg> add Conda #    Jupyter -    pkg> add IJulia #      pkg> build IJulia #     build

Agora para as tarefas!

Carregar equação

Na física, o termo transferência é entendido como processos irreversíveis, como resultado do qual ocorre um movimento espacial (transferência) de massa, momento, energia, carga ou alguma outra quantidade física no sistema físico.
A equação linear unidimensional de transporte (ou a equação de advecção) - a equação diferencial parcial mais simples - é escrita como

f r a c U p a r c i a l (x, t) p a r c i a l t + c f r a c U p a r c i a l (x, t) p a r c i a l x = P h i (U, x, t)

$\ frac {\ U parcial (x, t)} {\ parcial t} + c \ frac {\ U parcial (x, t)} {\ parcial x} = \ Phi (U, x, t)$

Para a solução numérica da equação de transporte, você pode usar o esquema de diferenças explícitas:

f r a c h a t U_{i} - U_{i} t a u + c f r a c U_{i} - U_{i - 1} D e l t a = f r a c P h i_{i - 1} + P h i_{i} 2

$\ frac {\ hat {U} _i-U_i} {\ tau} + c \ frac {U_i-U_ {i-1}} {\ Delta} = \ frac {\ Phi_ {i-1} + \ Phi_i} {2}$

onde $\ hat {U}$ - o valor da função de grade na camada de tempo superior. Este circuito é estável com o número de Courant. $K = c \ tau / \ Delta <1$

Transferência não linear

f r a c U p a r c i a l (x, t) p a r c i a l t + (C_{0} + U C_{1}) f r a c U p a r c i a l (x, t) p a r c i a l x = P h i (U, x, t)

$\ frac {\ U parcial (x, t)} {\ parcial t} + (C_0 + UC_1) \ frac {\ U parcial (x, t)} {\ parcial x} = \ Phi (U, x, t )$

Fonte da linha (transferência de absorção): $\ Phi (U, x, t) = - BU$ . Usamos o esquema de diferença explícita:

U_{i}^{j + 1} = l e f t (1 - f r a c h_{t} B 2 - f r a c h_{t} C_{0} h_{x} - f r a c h_{t} C_{1} h_{x} U_{i}^{j} r i g h t) U_{i}^{j} + U_{i - 1}^{j} l e f t (f r a c h_{t} C_{0} h_{x} - f r a c h_{t} B 2 + f r a c h_{t} C_{1} h_{x} U_{i}^{j} r i g h t)

$U ^ {j + 1} _i = \ left (1- \ frac {h_tB} {2} - \ frac {h_tC_0} {h_x} - \ frac {h_tC_1} {h_x} U ^ j_i \ right) U ^ j_i + U ^ j_ {i-1} \ left (\ frac {h_tC_0} {h_x} - \ frac {h_tB} {2} + \ frac {h_tC_1} {h_x} U ^ j_i \ right)$

 using Plots pyplot() a = 0.2 b = 0.01 ust = x -> x^2 * exp( -(xa)^2/b ) #   bord = t -> 0. #  #    - function transferequi(;C0 = 1., C1 = 0., B = 0., Nx = 50, Nt = 50, tlmt = 0.01) dx = 1/Nx dt = tlmt/Nt b0 = 0.5B*dt c0 = C0*dt/dx c1 = C1*dt/dx print("Kurant: $c0 $c1") x = [i for i in range(0, length = Nx, step = dx)]#         t = [i for i in range(0, length = Nt, step = dt)] #   -   U = zeros(Nx, Nt) U[:,1] = ust.(x) U[1,:] = bord.(t) for j = 1:Nt-1, i = 2:Nx U[i, j+1] = ( 1-b0-c0-c1*U[i,j] )*U[i,j] + ( c0-b0+c1*U[i,j] )*U[i-1,j] end t, x, U end t, X, Ans0 = transferequi( C0 = 4., C1 = 1., B = 1.5, tlmt = 0.2 ) plot(X, Ans0[:,1], lab = "t1") plot!(X, Ans0[:,10], lab = "t10") p = plot!(X, Ans0[:,40], lab = "t40") plot( p, heatmap(t, X, Ans0) ) #

Resultado

Vamos aumentar a absorção:

 t, X, Ans0 = transferequi( C0 = 2., C1 = 1., B = 3.5, tlmt = 0.2 ) plot(X, Ans0[:,1]) plot!(X, Ans0[:,10]) p = plot!(X, Ans0[:,40]) plot( p, heatmap(t, X, Ans0) )

Resultado

 t, X, Ans0 = transferequi( C0 = 1., C1 = 15., B = 0.1, Nx = 100, Nt = 100, tlmt = 0.4 ) plot(X, Ans0[:,1]) plot!(X, Ans0[:,20]) plot!(X, Ans0[:,90])

Quase derrubado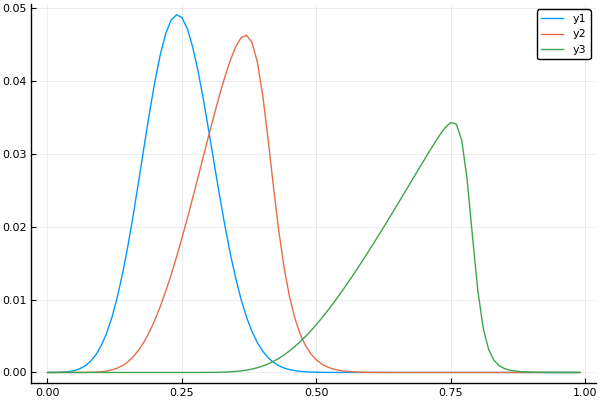

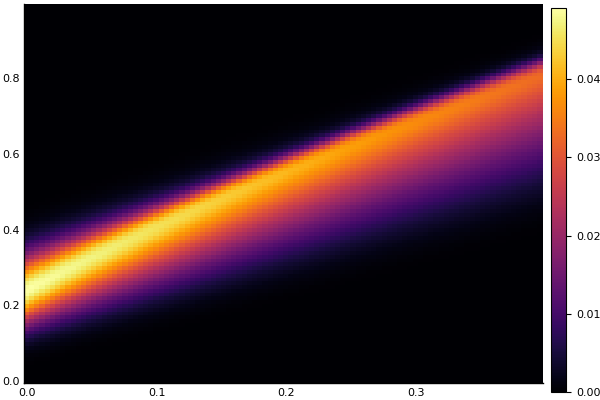
heatmap(t, X, Ans0)

Equação do calor

A equação diferencial de calor (ou a equação de difusão de calor) é escrita da seguinte forma:

f r a c p a r c i a l T (x, t) p a r c i a l t + D f r a c p a r c i a l^{2} U (x, t) p a r c i a l x^{2} = p h i (T, x, t)

$\ frac {\ parcial T (x, t)} {\ parcial t} + D \ frac {\ parcial ^ 2 U (x, t)} {\ parcial x ^ 2} = \ phi (T, x, t )$

Esta é uma equação parabólica que contém a primeira derivada em relação ao tempo te a segunda em relação à coordenada espacial x. Ele descreve a dinâmica da temperatura, por exemplo, de uma haste de metal de resfriamento ou aquecimento (a função T descreve o perfil de temperatura ao longo da coordenada x ao longo da haste). O coeficiente D é chamado coeficiente de condutividade térmica (difusão). Pode ser constante ou depender, explicitamente das coordenadas e da função desejada D (t, x, T).

Considere a equação linear (o coeficiente de difusão e as fontes de calor são independentes da temperatura). A aproximação da diferença de uma equação diferencial usando os esquemas de Euler explícitos e implícitos, respectivamente:

f r a c T_{i, n + 1} - T_{i, n} t a u = D f r a c T_{i - 1, n} - 2 T_{i, n} + T_{i + 1, n} D e l t a^{2} + p h i_{i, n} f r a c T_{i, n + 1} - T_{i, n} t a u = D f r a c T_{i - 1, n + 1} - 2 T_{i, n + 1} + T_{i + 1, n + 1} D e l t a^{2} + p h i_{i, n}

$\ frac {T_ {i, n + 1} -T_ {i, n}} {\ tau} = D \ frac {T_ {i-1, n} -2T_ {i, n} + T_ {i + 1 , n}} {\ Delta ^ 2} + \ phi_ {i, n} \\ \ frac {T_ {i, n + 1} -T_ {i, n}} {\ tau} = D \ frac {T_ { i-1, n + 1} -2T_ {i, n + 1} + T_ {i + 1, n + 1}} {\ Delta ^ 2} + \ phi_ {i, n}$

 δ(x) = x==0 ? 0.5 : x>0 ? 1 : 0 # -     startcond = x-> δ(x-0.45) - δ(x-0.55) #   bordrcond = x-> 0. #    D(u) = 1 #   Φ(u) = 0 #    #      LaTex    Tab # \delta press Tab -> δ function linexplicit(Nx = 50, Nt = 40; tlmt = 0.01) dx = 1/Nx dt = tlmt/Nt k = dt/(dx*dx) print("Kurant: $k dx = $dx dt = $dt k<0.5? $(k<0.5)") x = [i for i in range(0, length = Nx, step = dx)] #         t = [i for i in range(0, length = Nt, step = dt)] #   -   U = zeros(Nx, Nt) U[: ,1] = startcond.(x) U[1 ,:] = U[Nt,:] = bordrcond.(t) for j = 1:Nt-1, i = 2:Nx-1 U[i, j+1] = U[i,j]*(1-2k*D( U[i,j] )) + k*U[i-1,j]*D( U[i-1,j] ) + k*U[i+1,j]*D( U[i+1,j] ) + dt*Φ(U[i,j]) end t, x, U end t, X, Ans2 = linexplicit( tlmt = 0.005 ) plot(X, Ans2[:,1], lab = "t1") plot!(X, Ans2[:,10], lab = "t10") p = plot!(X, Ans2[:,40], lab = "t40", title = "Explicit scheme") plot( p, heatmap(t, X, Ans2) )

Resultado

Usamos o esquema implícito e o método sweep

 function nonexplicit(Nx = 50, Nt = 40; tlmt = 0.01) dx = 1/Nx dt = tlmt/Nt k = dt/(dx*dx) print("Kurant: $k dx = $dx dt = $dt k<0.5? $(k<0.5)\n") x = [i for i in range(0, length = Nx, step = dx)] t = [i for i in range(0, length = Nt, step = dt)] U = zeros(Nx, Nt) η = zeros(Nx+1) ξ = zeros(Nx) U[: ,1] = startcond.(x) U[1 ,:] = bordrcond.(t) U[Nt,:] = bordrcond.(t) for j = 1:Nt-1 b = -1 - 2k*D( U[1,j] ) c = -k*D( U[2,j] ) d = U[1,j] + dt*Φ(U[1,j]) ξ[2] = c/b η[2] = -d/b for i = 2:Nx-1 a = -k*D( U[i-1,j] ) b = -2k*D( U[i,j] ) - 1 c = -k*D( U[i+1,j] ) d = U[i,j] + dt*Φ(U[i,j]) ξ[i+1] = c / (ba*ξ[i]) η[i+1] = (a*η[i]-d) / (ba*ξ[i]) end U[Nx,j+1] = η[Nx] for i = Nx:-1:2 U[i-1,j+1] = ξ[i]*U[i,j+1] + η[i] end end t, x, U end plot(X, Ans2[:,1], lab = "ex_t1") plot!(X, Ans2[:,10], lab = "ex_t10") plot!(X, Ans2[:,40], lab = "ex_t40") plot!(X, Ans3[:,1], lab = "non_t1") plot!(X, Ans3[:,10], lab = "non_t10") plot!(X, Ans3[:,40], lab = "non_t40", title = "Comparison schemes")

Comparação de circuitos

Equação de calor não linear

Soluções muito mais interessantes podem ser obtidas para a equação de calor não linear, por exemplo, com uma fonte de calor não linear $\ phi (x, T) = 10 ^ 3 (T-T ^ 3)$ . Se você o definir desta forma, obterá uma solução na forma de frentes térmicas, propagando-se nos dois lados da zona de aquecimento primário

 Φ(u) = 1e3*(uu^3) t, X, Ans4 = linexplicit( tlmt = 0.005 ) plot(X, Ans4[:,1], lab = "ex_t1") plot!(X, Ans4[:,10], lab = "ex_t10") plot!(X, Ans4[:,40], lab = "ex_t40", title = "Thermal front")

Frente térmica

Soluções ainda mais inesperadas são possíveis com a não linearidade do coeficiente de difusão. Por exemplo, se você tomar $D (x, T) = T ^ 2$ , um $\ phi (x, T) = 10 ^ 3T ^ {3.5}$ , pode-se observar o efeito da combustão do meio, localizado na região de seu aquecimento primário (modo S de combustão “com exacerbação”).
Ao mesmo tempo, verificaremos como nosso esquema implícito funciona com a não linearidade das fontes e do coeficiente de difusão

 D(u) = u*u Φ(u) = 1e3*abs(u)^(3.5) t, X, Ans5 = linexplicit( tlmt = 0.0005 ) t, X, Ans6 = nonexplicit( tlmt = 0.0005 ) plot(X, Ans5[:,1], lab = "ex_t1") plot!(X, Ans5[:,10], lab = "ex_t10") p1 = plot!(X, Ans5[:,40], lab = "ex_t40", title = "Burning with aggravation") p2 = heatmap(abs.(Ans6-Ans5), title = "Difference") #      plot(p1, p2)

Modo S

Equação de onda

Equação da Onda Hiperbólica

f r a c p a r c i a l^{2} U (x, t) p a r c i a l t^{2} = c^{2} f r a c p a r c i a l^{2} U (x, t) p a r c i a l x^{2}

$\ frac {\ parcial ^ 2 U (x, t)} {\ parcial t ^ 2} = c ^ 2 \ frac {\ parcial ^ 2 U (x, t)} {\ parcial x ^ 2}$

descreve ondas lineares unidimensionais sem dispersão. Por exemplo, vibrações de uma corda, som em um líquido (gás) ou ondas eletromagnéticas no vácuo (neste último caso, a equação deve ser escrita em forma vetorial).

O esquema de diferenças mais simples que se aproxima dessa equação é um esquema explícito de cinco pontos

f r a c U_{i}^{n + 1} - 2 U_{i}^{n} + U_{i}^{n - 1} t a u^{2} = c^{2} f r a c U_{i + 1}^{n} - 2 U_{i}^{n} + U_{i - 1}^{n} h^{2} x_{i} = i h, t_{n} = t a u

$\ frac {U ^ {n + 1} _i-2U ^ {n} _i + U ^ {n-1} _i} {\ tau ^ 2} = c ^ 2 \ frac {U ^ n_ {i + 1} -2U ^ n_i + U ^ n_ {i-1}} {h ^ 2} \\ x_i = ih, \, t_n = \ tau$

Esse esquema, chamado de "cruz", tem uma segunda ordem de precisão no tempo e nas coordenadas espaciais e possui três camadas no tempo.

 #     ψ = x -> x^2 * exp( -(x-0.5)^2/0.01 ) #    ϕ(x) = 0 c = x -> 1 #     function pdesolver(N = 100, K = 100, L = 2pi, T = 10, a = 0.1 ) dx = L/N; dt = T/K; gam(x) = c(x)*c(x)*a*a*dt*dt/dx/dx; print("Kurant-Fridrihs-Levi: $(dt*a/dx) dx = $dx dt = $dt") u = zeros(N,K); x = [i for i in range(0, length = N, step = dx)] #      u[:,1] = ψ.(x); u[:,2] = u[:,1] + dt*ψ.(x); #     fill!( u[1,:], 0); fill!( u[N,:], ϕ(L) ); for t = 2:K-1, i = 2:N-1 u[i,t+1] = -u[i,t-1] + gam( x[i] )* (u[i-1,t] + u[i+1,t]) + (2-2*gam( x[i] ) )*u[i,t]; end x, u end N = 50; #     K = 40; #    a = 0.1; #    L = 1; #   T = 1; #   t = [i for i in range(0, length = K, stop = T)] X, U = pdesolver(N, K, L, T, a) #    plot(X, U[:,1]) plot!(X, U[:,40])

Resultado

Para construir uma superfície, usaremos o PyPlot como um ambiente de plotagens, mas diretamente:

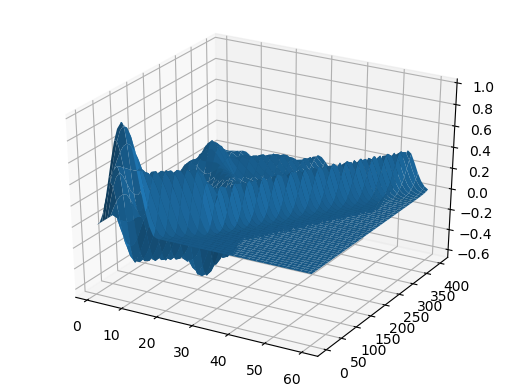
Gráfico de superfície

 using PyPlot surf(t, X, U)

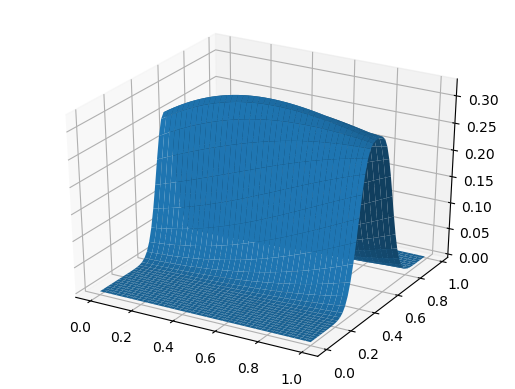
E para a sobremesa, a onda se propaga a uma velocidade, dependendo da coordenada:

 ψ = x -> x>1/3 ? 0 : sin(3pi*x)^2 c = x -> x>0.5 ? 0.5 : 1 X, U = pdesolver(400, 400, 8, 1.5, 1) plot(X, U[:,1]) plot!(X, U[:,40]) plot!(X, U[:,90]) plot!(X, U[:,200], xaxis=("  ", (0, 1.5), 0:0.5:2) )

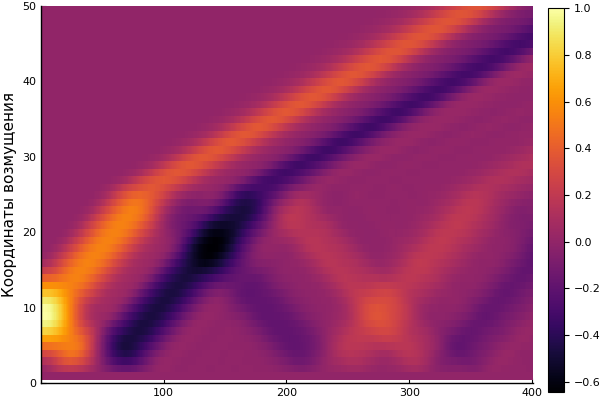
Resultado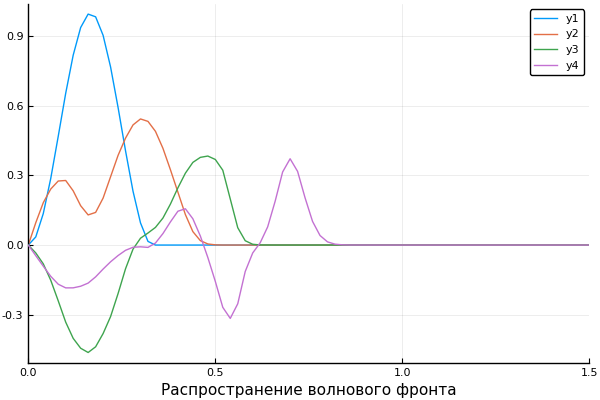

 U2 = [ U[i,j] for i = 1:60, j = 1:size(U,2) ] #    surf(U2) #

heatmap(U, yaxis=(" ", (0, 50), 0:10:50))

O suficiente por hoje. Para uma revisão mais detalhada:
O PyPlot está vinculado ao github , outros exemplos de plotagens sendo usados como ambiente e um bom memorando em russo da Julia .

Julia e equações diferenciais parciais

Carregar equação

Transferência não linear

Equação do calor

Equação de calor não linear

Equação de onda

More articles: