Um codificador automático variacional (codificador automático) é um modelo generativo que aprende a exibir objetos em um determinado espaço oculto.

Você já se perguntou como funciona um modelo de codificador automático variacional (VAE)? Deseja saber como o VAE gera novos exemplos, como o conjunto de dados em que foi treinado? Depois de ler este artigo, você obterá uma compreensão teórica do funcionamento interno do VAE e também poderá implementá-lo. Em seguida, mostrarei o código VAE de trabalho treinado em um conjunto de dígitos escritos à mão e nos divertiremos, gerando novos dígitos!

Modelos Generativos

O VAE é um modelo generativo - estima a densidade de probabilidade (PDF) dos dados de treinamento. Se esse modelo for treinado em imagens naturais, ele atribuirá um valor de alta probabilidade à imagem do leão e um valor baixo à imagem de besteira aleatória.

O modelo VAE também pode obter exemplos de PDF treinado, que é a parte mais interessante, pois pode gerar novos exemplos semelhantes ao conjunto de dados original!

Explicarei o VAE usando o conjunto de números manuscritos MNIST . Os dados de entrada para o modelo são figuras no formato $$$\ mathbb {R} ^ {28 × 28}$ . O modelo deve avaliar a probabilidade de quanto a entrada se parece com um dígito.

Tarefa de modelagem de imagem

A interação entre pixels é uma tarefa difícil. Se os pixels forem independentes um do outro, você precisará estudar o PDF de cada pixel de forma independente, o que é fácil. A seleção também é simples - pegamos cada pixel separadamente.

Mas nas imagens digitais, existem claras dependências entre os pixels. Se você vir o início dos quatro na metade esquerda, ficará surpreso se a metade direita for a conclusão de zero. Mas porque?

Espaço oculto

Você sabe que cada imagem tem um número. Entrada para $$$\ mathbb {R} ^ {28 × 28}$ claramente não contém essas informações. Mas deve estar em algum lugar ... Esse "lugar" é um espaço oculto.



Você pode pensar no espaço oculto como $$$\ mathbb {R} ^ {k}$ onde cada vetor contém $$$k$ informações necessárias para renderizar uma imagem. Suponha que a primeira dimensão contenha um número representado por um dígito. A segunda dimensão pode ser largura. O terceiro é o ângulo, e assim por diante.

Podemos imaginar o processo de desenhar uma pessoa em duas etapas. Primeiro, uma pessoa determina - conscientemente ou não - todos os atributos do número que será exibido. Em seguida, essas decisões são transformadas em traços no papel.

O VAE está tentando simular esse processo: para uma determinada imagem $$$x$ queremos encontrar pelo menos um vetor oculto que possa descrevê-lo; um vetor contendo instruções para gerar $$$x$ . Formulando-o pela fórmula da probabilidade total , obtemos $$$P (x) = \ int P (x | z) P (z) dz$ .

Vamos colocar algum sentido razoável nessa equação:

• Integral significa que os candidatos devem ser procurados em todo o espaço oculto.
• Para cada candidato $$$z$ fazemos a pergunta: é possível gerar $$$x$ usando instruções $$$z$ ? É grande o suficiente $$$P (x | z)$ ? Por exemplo, se $$$z$ codifica informações sobre o dígito 7, a imagem 8 não é possível. No entanto, a imagem 1 é aceitável porque 1 e 7 são semelhantes.
• Encontramos uma boa. $$$z$ ? Ótimo! Mas espere um segundo ... quanto custa $$$z$ provavelmente? $$$P (z)$ grande o suficiente? Considere a imagem do número invertido 7. Uma correspondência ideal seria um vetor oculto que descreve a vista 7, em que o tamanho do ângulo é definido em 180 °. No entanto, tais $$$z$ É improvável, porque geralmente os números não são escritos em um ângulo de 180 °.

O objetivo do treinamento da VAE é maximizar $$$P (x)$ . Modelaremos $$$P (x | z)$ usando distribuição gaussiana multidimensional $$$\ mathcal {N} (f (z), \ sigma ^ 2 \ cdot I)$ .

$$$f (z)$ modelado usando uma rede neural. $$$\ sigma$ É um hiperparâmetro para multiplicar a matriz de identidade $$$I$ .

Tenha em mente que $$$f$ - é isso que usaremos para gerar novas imagens usando um modelo treinado. A sobreposição de uma distribuição gaussiana é apenas para fins educacionais. Se usarmos a função delta Dirac (ou seja, determinística $$$x = f (z)$ ), não poderemos treinar o modelo usando descida gradiente!

As maravilhas do espaço oculto

A abordagem do espaço oculto tem dois grandes problemas:

1. Quais informações cada dimensão contém? Algumas dimensões podem estar relacionadas a elementos abstratos, como estilo. Mesmo se fosse fácil interpretar todas as dimensões, não queremos atribuir rótulos ao conjunto de dados. Essa abordagem não se ajusta a outros conjuntos de dados.
2. O espaço oculto pode ser confundido quando há uma correlação entre as dimensões. Por exemplo, um número muito rapidamente desenhado pode levar ao aparecimento de traços angulares e mais finos. Definir essas dependências é difícil.

O aprendizado profundo vem em socorro

Acontece que cada distribuição pode ser gerada aplicando uma função bastante complexa à distribuição gaussiana multidimensional padrão.

Escolha $$$P (z)$ como uma distribuição gaussiana multidimensional padrão. Assim modelado por uma rede neural $$$f$ pode ser dividido em duas fases:

1. As primeiras camadas mapeiam a distribuição gaussiana na verdadeira distribuição no espaço oculto. Não podemos interpretar as medidas, mas isso não importa.
2. Camadas subsequentes serão exibidas do espaço oculto no $$$P (x | z)$ .

Então, como treinamos essa fera?

Fórmula para $$$P (x)$ insolúvel, portanto, o aproximamos pelo método de Monte Carlo:

1. Selecção $$$\ {z_i \} _ {i = 1} ^ n$ do anterior $$$P (z)$
2. Aproximação com $$$P (x) \ approx \ frac {1} {n} \ sum_ {i = 1} ^ n P (x | z_i)$

Ótimo! Então, tente várias coisas diferentes $$$z$ e inicie a festa de propagação de bugs!

Infelizmente desde $$$x$ muito multidimensional, para obter uma aproximação razoável, são necessárias muitas amostras. Quero dizer, se você tentar $$$z$ , quais são as chances de obter uma imagem parecida com $$$x$ ? A propósito, isso explica por que $$$P (x | z)$ deve atribuir um valor de probabilidade positivo a qualquer imagem possível; caso contrário, o modelo não poderá aprender: amostragem $$$z$ resultará em uma imagem quase certamente diferente de $$$x$ e se a probabilidade for 0, os gradientes não poderão se propagar.

Como resolver este problema?

Corte o caminho!

Maioria das amostras $$$z$ nada será adicionado da seleção para $$$P (x)$ - Eles estão muito além de suas fronteiras. Agora, se você soubesse com antecedência de onde levá-los ...

Pode entrar $$$Q (z | x)$ . Dado $$$Q$ será treinado para atribuir altos valores de probabilidade a $$$z$ que provavelmente geram $$$x$ . Agora você pode fazer uma avaliação usando o método Monte Carlo, colhendo muito menos amostras de $$$Q$ .

Infelizmente, um novo problema surge! Em vez de maximizar $$$P (x) = \ int P (x | z) P (z) dz = \ mathbb {E} _ {z \ sim P (z)} P (x | z)$ nós maximizamos $$$\ mathbb {E} _ {z \ sim Q (z | x)} P (x | z)$ . Como eles se relacionam?

Conclusão variacional

A conclusão variacional é o tópico de um artigo separado, por isso não vou me debruçar sobre isso aqui em detalhes. Só posso dizer que essas distribuições estão relacionadas por esta equação:

$$

$$log P (X) - \ mathcal {KL} [Q (z | x) || P (z | x)] = \ mathbb {E} _ {z \ sim Q (z | x)} [log P (x | z)] - \ mathcal {KL} [Q (z | x) || P (z)]$$

$$$\ mathcal {KL}$ é a distância Kullback - Leibler , que avalia intuitivamente a semelhança das duas distribuições.

Em um momento, você verá como maximizar o lado direito da equação. Nesse caso, o lado esquerdo também é maximizado:

• $$$P (x)$ maximizado.
• a que distância $$$Q (z | x)$ de $$$P (z | x)$ - real a priori desconhecido - será minimizado.

O significado do lado direito da equação é que temos tensão aqui:

1. Por um lado, queremos maximizar o quão bem $$$x$ deve ser decodificado de $$$z \ sim Q$ .
2. Por outro lado, queremos $$$Q (z | x)$ ( codificador ) foi semelhante ao anterior $$$P (z)$ (distribuição gaussiana multidimensional). Isso pode ser visto como regularização.

Minimização de divergência $$$\ mathcal {KL}$ executado facilmente com a seleção certa de distribuições. Vamos simular $$$Q (z | x)$ como uma rede neural, cuja saída são os parâmetros de uma distribuição gaussiana multidimensional:

• média $$$\ mu_Q$
• matriz de covariância diagonal $$$\ Sigma_Q$

Então divergência $$$\ mathcal {KL}$ torna-se analiticamente solucionável, o que é ótimo para nós (e para gradientes).

A parte do decodificador é um pouco mais complicada. À primeira vista, gostaria de afirmar que esse problema é insolúvel pelo método de Monte Carlo. Mas a amostra $$$z$ de $$$Q$ não permitirá que os gradientes se propaguem através $$$Q$ , porque a seleção não é uma operação diferenciável. Isso é um problema, desde então os pesos das camadas que emitem $$$\ Sigma_Q$ e $$$\ mu_Q$ .

Novo truque de parametrização

Nós podemos substituir $$$Q$ transformação parametrizada determinística de uma variável aleatória não paramétrica:

1. Uma amostra da distribuição gaussiana padrão (sem parâmetros).
2. Multiplicando a amostra pela raiz quadrada $$$\ Sigma_Q$ .
3. Adicionando ao resultado $$$\ mu_Q$ .

Como resultado, obtemos uma distribuição igual a $$$Q$ . Agora, a operação de busca vem da distribuição Gaussiana padrão. Consequentemente, os gradientes podem se propagar através de $$$\ Sigma_Q$ e $$$\ mu_Q$ já que agora esses são caminhos determinísticos.

Resultado? O modelo poderá aprender como ajustar os parâmetros $$$Q$ : ela vai se concentrar em torno do bem $$$z$ que são capazes de produzir $$$x$ .

Juntando tudo

O modelo VAE pode ser difícil de entender. Examinamos aqui muito material que é difícil de digerir.

Deixe-me resumir todas as etapas para a implementação do VAE.



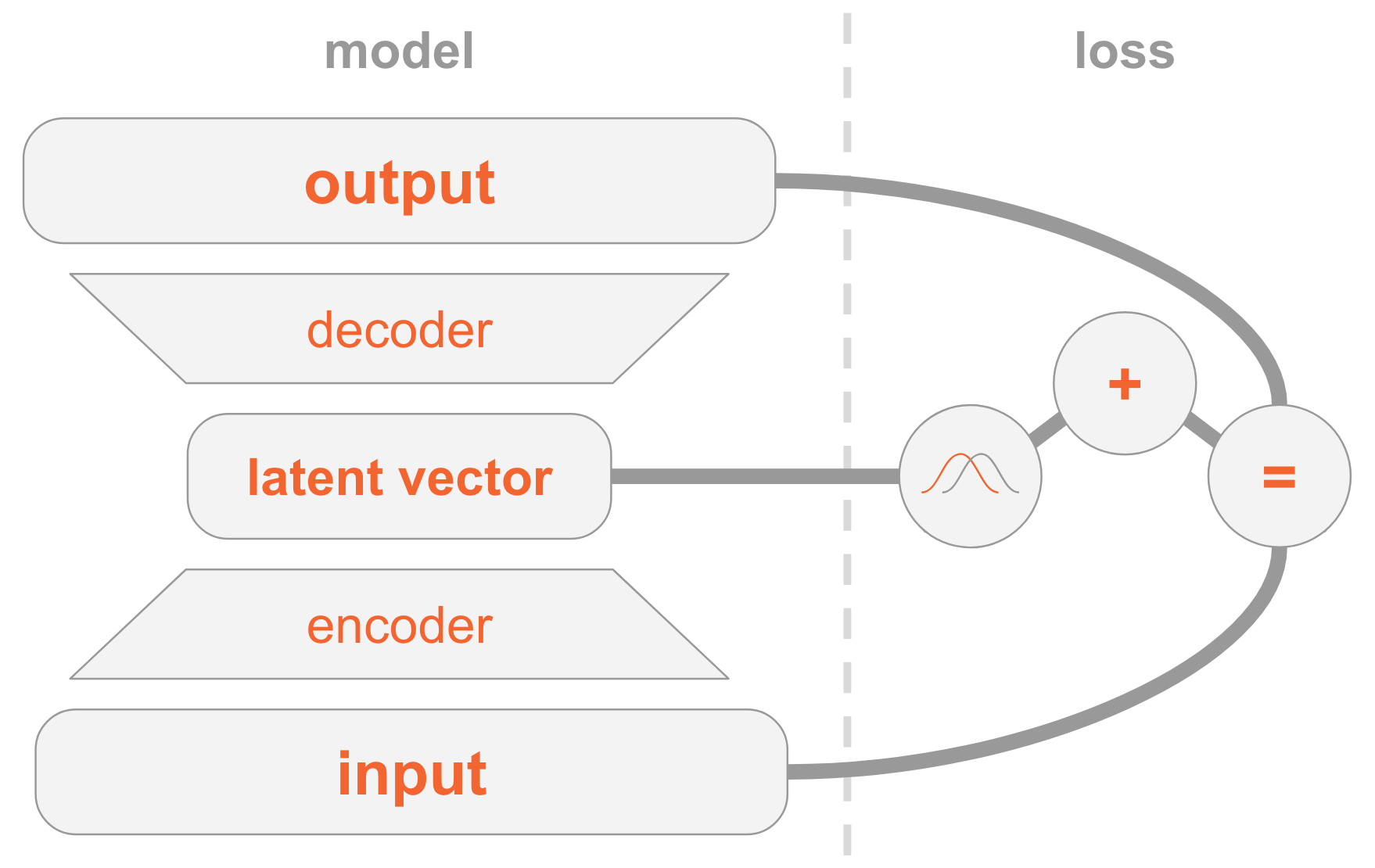
À esquerda, temos uma definição de modelo:

1. A imagem de entrada é transmitida através da rede do codificador.
2. O codificador fornece parâmetros de distribuição $$$Q (z | x)$ .
3. Vetor oculto $$$z$ tirado de $$$Q (z | x)$ . Se o codificador estiver bem treinado, na maioria dos casos $$$z$ contém uma descrição $$$x$ .
4. Decodificador decodifica $$$z$ na imagem.

No lado direito, temos uma função de perda:

1. Erro de recuperação: a saída deve ser semelhante à entrada.
2. $$$Q (z | x)$ deve ser semelhante ao anterior, ou seja, uma distribuição normal padrão multidimensional.

Para criar novas imagens, você pode selecionar diretamente o vetor oculto da distribuição anterior e decodificá-lo em uma imagem.

Código de trabalho

Agora vamos estudar o VAE em mais detalhes e considerar o código de trabalho. Você entenderá todos os detalhes técnicos necessários para implementar o VAE. Como bônus, mostrarei um truque interessante: como atribuir funções especiais a algumas dimensões do vetor oculto para que o modelo comece a gerar imagens dos números indicados.

import numpy as np import tensorflow as tf from tensorflow.examples.tutorials.mnist import input_data import matplotlib.pyplot as plt np.random.seed(42) tf.set_random_seed(42) %matplotlib inline 

Lembro que os modelos são treinados no MNIST - um conjunto de números manuscritos. As imagens de entrada vêm no formato $$$\ mathbb {R} ^ {28 × 28}$ .

 mnist = input_data.read_data_sets('MNIST_data') input_size = 28 * 28 num_digits = 10 

Em seguida, definimos hiperparâmetros.

Sinta-se livre para jogar com valores diferentes para ter uma idéia de como eles afetam o modelo.

 params = { 'encoder_layers': [128], #       'decoder_layers': [128], #    (CNN ,     ) 'digit_classification_layers': [128], #   ,   'activation': tf.nn.sigmoid, #      'decoder_std': 0.5, #   P(x|z)   'z_dim': 10, #    'digit_classification_weight': 10.0, #   ,   'epochs': 20, 'batch_size': 100, 'learning_rate': 0.001 } 

Modelo

O modelo consiste em três sub-redes:

1. Obtém $$$x$ (imagem), codifica-o em uma distribuição $$$Q (z | x)$ no espaço escondido.
2. Obtém $$$z$ no espaço oculto (representação de código da imagem), decodifica-a na imagem correspondente $$$f (z)$ .
3. Obtém $$$x$ e determina o número por comparação com a camada 10-dimensional, onde o i-ésimo valor contém a probabilidade do i-ésimo número.

As duas primeiras sub-redes são a base do VAE puro.

A terceira é uma tarefa auxiliar que usa algumas das dimensões ocultas para codificar os números encontrados na imagem. Vou explicar o porquê: discutimos anteriormente que não nos importamos com as informações que cada dimensão do espaço oculto contém. Um modelo pode aprender a codificar qualquer informação que considere valiosa para sua tarefa. Como estamos familiarizados com o conjunto de dados, sabemos a importância da dimensão, que contém o tipo de dígito (ou seja, seu valor numérico). E agora queremos ajudar o modelo, fornecendo a ela essas informações.

Para um determinado tipo de dígito, nós o codificamos diretamente, ou seja, usamos um vetor de tamanho 10. Esses dez números estão associados a um vetor oculto; portanto, ao decodificar esse vetor em uma imagem, o modelo utilizará informações digitais.

Existem duas maneiras de fornecer modelos vetoriais de codificação direta:

1. Inclua-o como entrada no modelo.
2. Adicione-o como um rótulo, para que o próprio modelo calcule a previsão: adicionaremos outra sub-rede que prevê um vetor 10-dimensional, onde a função de perda é a entropia cruzada com o vetor de codificação direta esperado.

Escolha a segunda opção. Porque Bem, ao testar, você pode usar o modelo de duas maneiras:

1. Especifique a imagem como entrada e exiba um vetor oculto.
2. Especifique um vetor oculto como entrada e gere uma imagem.

Como queremos oferecer suporte à primeira opção, não podemos fornecer um dígito ao modelo como entrada, porque não queremos conhecê-lo durante o teste. Portanto, o modelo deve aprender a prever.

 def encoder(x, layers): for layer in layers: x = tf.layers.dense(x, layer, activation=params['activation']) mu = tf.layers.dense(x, params['z_dim']) var = 1e-5 + tf.exp(tf.layers.dense(x, params['z_dim'])) return mu, var def decoder(z, layers): for layer in layers: z = tf.layers.dense(z, layer, activation=params['activation']) mu = tf.layers.dense(z, input_size) return tf.nn.sigmoid(mu) def digit_classifier(x, layers): for layer in layers: x = tf.layers.dense(x, layer, activation=params['activation']) logits = tf.layers.dense(x, num_digits) return logits 

 images = tf.placeholder(tf.float32, [None, input_size]) digits = tf.placeholder(tf.int32, [None]) #        encoder_mu, encoder_var = encoder(images, params['encoder_layers']) #     ,  #     eps = tf.random_normal(shape=[tf.shape(images)[0], params['z_dim']], mean=0.0, stddev=1.0) z = encoder_mu + tf.sqrt(encoder_var) * eps # classify the digit digit_logits = digit_classifier(images, params['digit_classification_layers']) digit_prob = tf.nn.softmax(digit_logits) #     ,  #    decoded_images = decoder(tf.concat([z, digit_prob], axis=1), params['decoder_layers']) 

 #    ,    #    loss_reconstruction = -tf.reduce_sum( tf.contrib.distributions.Normal( decoded_images, params['decoder_std'] ).log_prob(images), axis=1 ) #         . #      , #         #  ,  KL-   # ,    loss_prior = -0.5 * tf.reduce_sum( 1 + tf.log(encoder_var) - encoder_mu ** 2 - encoder_var, axis=1 ) loss_auto_encode = tf.reduce_mean( loss_reconstruction + loss_prior, axis=0 ) # digit_classification_weight      , #      loss_digit_classifier = params['digit_classification_weight'] * tf.reduce_mean( tf.nn.sparse_softmax_cross_entropy_with_logits(labels=digits, logits=digit_logits), axis=0 ) loss = loss_auto_encode + loss_digit_classifier train_op = tf.train.AdamOptimizer(params['learning_rate']).minimize(loss) 

Treinamento

Treinaremos um modelo para otimizar duas funções de perda - VAE e classificação - usando SGD .

No final de cada época, selecionamos vetores ocultos e os decodificamos em imagens para observar visualmente como o poder generativo do modelo melhora ao longo das épocas. O método de amostragem é o seguinte:

1. Defina explicitamente as dimensões usadas para classificar pelo dígito que queremos gerar. Por exemplo, se queremos criar uma imagem do número 2, definimos as medidas $$$[0010000000]$ .
2. Selecione aleatoriamente dentre outras dimensões da distribuição normal multidimensional. Estes são os valores para os diferentes números que são gerados nesta época. Então, temos uma idéia do que é codificado em outras dimensões, por exemplo, estilo de escrita à mão.

O significado da etapa 1 é que, após a convergência, o modelo deve ser capaz de classificar a figura na imagem de entrada por essas configurações de medição. No entanto, eles também são usados ​​na fase de decodificação para criar uma imagem. Ou seja, a sub-rede do decodificador sabe: quando as medições correspondem ao número 2, deve gerar uma imagem com esse número. Portanto, se definirmos manualmente as medidas para o número 2, obteremos uma imagem gerada dessa figura.

 samples = [] losses_auto_encode = [] losses_digit_classifier = [] with tf.Session() as sess: sess.run(tf.global_variables_initializer()) for epoch in xrange(params['epochs']): for _ in xrange(mnist.train.num_examples / params['batch_size']): batch_images, batch_digits = mnist.train.next_batch(params['batch_size']) sess.run(train_op, feed_dict={images: batch_images, digits: batch_digits}) train_loss_auto_encode, train_loss_digit_classifier = sess.run( [loss_auto_encode, loss_digit_classifier], {images: mnist.train.images, digits: mnist.train.labels}) losses_auto_encode.append(train_loss_auto_encode) losses_digit_classifier.append(train_loss_digit_classifier) sample_z = np.tile(np.random.randn(1, params['z_dim']), reps=[num_digits, 1]) gen_samples = sess.run(decoded_images, feed_dict={z: sample_z, digit_prob: np.eye(num_digits)}) samples.append(gen_samples) 

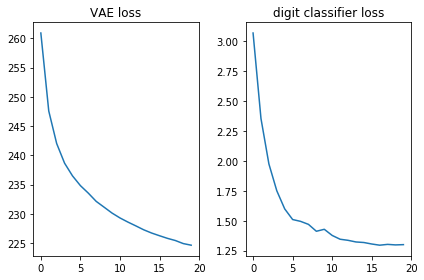
Vamos verificar se as duas funções de perda ficam bem, ou seja, elas diminuem:

 plt.subplot(121) plt.plot(losses_auto_encode) plt.title('VAE loss') plt.subplot(122) plt.plot(losses_digit_classifier) plt.title('digit classifier loss') plt.tight_layout() 

Além disso, vamos exibir as imagens geradas e ver se o modelo realmente pode criar imagens com números manuscritos:

 def plot_samples(samples): IMAGE_WIDTH = 0.7 plt.figure(figsize=(IMAGE_WIDTH * num_digits, len(samples) * IMAGE_WIDTH)) for epoch, images in enumerate(samples): for digit, image in enumerate(images): plt.subplot(len(samples), num_digits, epoch * num_digits + digit + 1) plt.imshow(image.reshape((28, 28)), cmap='Greys_r') plt.gca().xaxis.set_visible(False) if digit == 0: plt.gca().yaxis.set_ticks([]) plt.ylabel('epoch {}'.format(epoch + 1), verticalalignment='center', horizontalalignment='right', rotation=0, fontsize=14) else: plt.gca().yaxis.set_visible(False) plot_samples(samples) 

Conclusão

É bom ver que uma rede de distribuição direta simples (sem convulsões sofisticadas) gera belas imagens em apenas 20 épocas. O modelo aprendeu rapidamente a usar medidas especiais para números: na 9ª era, já vemos a sequência de números que estávamos tentando gerar.

Cada época usava valores aleatórios diferentes para outras dimensões; portanto, o estilo é diferente entre as épocas, mas é semelhante entre elas: pelo menos em algumas. Por exemplo, no dia 18, todos os números são mais gordos em comparação ao dia 20.

Anotações

O artigo é baseado na minha experiência e nas seguintes fontes:

• Conclusão variacional e aprendizado profundo: uma nova síntese
• Guia do codificador automático de variação