Curso MIT "Segurança de sistemas de computadores". Palestra 16: “Ataques de Canal Lateral”, Parte 1

Instituto de Tecnologia de Massachusetts. Curso de Aula nº 6.858. "Segurança de sistemas de computador". Nikolai Zeldovich, James Mickens. 2014 ano

Computer Systems Security é um curso sobre o desenvolvimento e implementação de sistemas de computador seguros. As palestras abrangem modelos de ameaças, ataques que comprometem a segurança e técnicas de segurança baseadas em trabalhos científicos recentes. Os tópicos incluem segurança do sistema operacional (SO), recursos, gerenciamento de fluxo de informações, segurança de idiomas, protocolos de rede, segurança de hardware e segurança de aplicativos da web.

Palestra 1: “Introdução: modelos de ameaças” Parte 1 / Parte 2 / Parte 3
Palestra 2: “Controle de ataques de hackers” Parte 1 / Parte 2 / Parte 3
Aula 3: “Estouros de Buffer: Explorações e Proteção” Parte 1 / Parte 2 / Parte 3
Palestra 4: “Separação de Privilégios” Parte 1 / Parte 2 / Parte 3
Palestra 5: “De onde vêm os sistemas de segurança?” Parte 1 / Parte 2
Palestra 6: “Oportunidades” Parte 1 / Parte 2 / Parte 3
Palestra 7: “Sandbox do Cliente Nativo” Parte 1 / Parte 2 / Parte 3
Aula 8: “Modelo de Segurança de Rede” Parte 1 / Parte 2 / Parte 3
Aula 9: “Segurança de aplicativos da Web” Parte 1 / Parte 2 / Parte 3
Palestra 10: “Execução Simbólica” Parte 1 / Parte 2 / Parte 3
Aula 11: “Linguagem de Programação Ur / Web” Parte 1 / Parte 2 / Parte 3
Aula 12: Segurança de rede Parte 1 / Parte 2 / Parte 3
Aula 13: “Protocolos de Rede” Parte 1 / Parte 2 / Parte 3
Palestra 14: “SSL e HTTPS” Parte 1 / Parte 2 / Parte 3
Palestra 15: “Software Médico” Parte 1 / Parte 2 / Parte 3
Palestra 16: “Ataques de Canal Lateral” Parte 1 / Parte 2 / Parte 3

Ok pessoal, vamos começar. Então, hoje falaremos sobre ataques através de canais laterais, um problema comum inerente a todos os tipos de sistemas. Em um sentido amplo, ataques pelo canal lateral ocorrem em uma situação em que você não acha que algumas informações são capazes de revelar informações sobre o seu sistema.



Normalmente, você tem vários componentes que estabelecem uma conexão entre o usuário e o servidor. Ao mesmo tempo, você pensa que sabe tudo o que passa por esse fio conectando dois assinantes, conhece todos os bits que o usuário e o servidor trocam entre si, e isso é seguro. Mas muitas vezes acontece que algumas informações ainda são divulgadas pelo usuário ou servidor. O exemplo descrito na palestra de hoje descreve uma situação em que a sincronização de mensagens entre o usuário e o servidor revela algumas informações adicionais que você não conheceria, apenas observando o fluxo de bits entre esses assinantes.

De fato, existe uma classe muito mais ampla de canais laterais com a qual você pode se preocupar. As pessoas aprenderam sobre a aparência dos canais laterais nos anos 40, quando descobriram que, se você começar a digitar caracteres em um teletipo, a eletrônica do teletipo começará a emitir radiação de radiofrequência. Nesse caso, você pode simplesmente colocar o osciloscópio próximo a ele e observar como a frequência do sinal de rádio muda dependendo do símbolo que o operador de teletipo imprime. Assim, a radiação de RF é um exemplo clássico de um canal lateral que faz você se preocupar.

Existem muitos outros exemplos observados pelas pessoas, como o consumo de eletricidade. Este é outro canal lateral com o qual você pode se preocupar, pois o computador utilizará uma quantidade diferente de energia, dependendo do cálculo.



Um exemplo de canal lateral é o som, devido ao qual o vazamento de informações também é possível. Por exemplo, as pessoas ouvem a impressora e, com base nos sons que emitem, podem dizer quais caracteres são impressos. Isso é especialmente fácil para impressoras matriciais que produzem sons muito irritantes durante a impressão.

Em geral, isso é algo para se pensar. Em uma palestra de segunda-feira, Kevin também mencionou alguns canais secundários interessantes com os quais ele lida em sua pesquisa. Mas vamos ver o canal lateral específico que David Bramley e Dan Bone estudaram. Em seu trabalho, publicado há cerca de 10 anos, eles escrevem que foram capazes de extrair a chave criptográfica do servidor da web Apache, medindo o tempo de respostas diferentes para vários pacotes de entrada de um cliente hostil. Nesse caso em particular, eles “procuravam” uma chave criptográfica. De fato, muitos ataques pelo canal lateral visam chaves criptográficas em parte porque é bastante difícil obter uma grande quantidade de dados através desse canal. E as chaves criptográficas são uma das situações em que um pequeno número de bits é gerado, ou seja, durante um ataque, os atacantes podem extrair de 200 a 256 bits de informação. Mas com base apenas nesses 200 bits, eles são capazes de decifrar a chave criptográfica desse servidor da web.

Se você estiver tentando acessar algum tipo de banco de dados cheio de números de previdência social, precisará “mesclar” muitas informações nele. É por isso que a maioria dos ataques de canal lateral se concentra em obter pequenos segredos, como chaves criptográficas ou senhas. Mas, em geral, isso se aplica a muitas outras situações.

Nos materiais das palestras, outra coisa interessante é descrita - é que tudo isso pode ser feito pela rede. Você provavelmente percebeu que eles tinham que fazer muito trabalho cuidadoso para detectar essas menores diferenças nas informações de tempo. Cada solicitação enviada ao servidor diferia de outra solicitação por 1 a 2 microssegundos, que é um período muito curto. Portanto, você deve ter muito cuidado, porque nossas redes não nos permitem capturar uma diferença tão temporária e determinam que o servidor processou sua solicitação por 1 a 2 microssegundos mais do que deveria.



Como resultado, não ficou claro se esse ataque poderia ser organizado em uma rede muito “barulhenta”, pois as informações úteis deveriam ser separadas do nível de ruído. Esses caras foram os primeiros a mostrar que você realmente pode fazer isso em uma rede Ethernet com um servidor em uma extremidade da rede e um cliente na outra extremidade. Eles provaram que é realmente possível medir essas diferenças em parte pela média, em parte por outros truques.
O plano para o restante desta palestra é o seguinte: primeiro, nos aprofundamos nos detalhes do algoritmo criptográfico de chave pública da RSA que esses caras usaram. Não o avaliaremos do ponto de vista da segurança, mas veremos como ele é implementado, porque é a implementação do algoritmo que é fundamental para o uso do canal lateral.

Bramley e Bone examinaram os vários detalhes da implementação para entender quando certas coisas eram mais rápidas ou mais lentas. Então, primeiro precisamos descobrir como o sistema de criptografia RSA é implementado e, em seguida, voltaremos e descobriremos como atacar todas essas estruturas disponíveis no RSA.

Vamos começar revisando o RSA em um nível alto. O RSA é um sistema de criptografia de chave pública bastante usado. Mencionamos esses caras algumas semanas atrás, quando conversamos sobre certificados. Agora vamos ver como ele realmente funciona.

Como regra, há três coisas com as quais você precisa se preocupar: geração de chaves, criptografia e descriptografia. No RSA, a maneira de criar uma chave é selecionar 2 números inteiros primos grandes, denotá-los por peq. Em seu artigo, esses caras escrevem sobre peq cada um com um tamanho de 512 bits. Isso geralmente é chamado de RSA de 1024 bits, porque o produto desses números primos é um número inteiro de 1000 bits. Atualmente, essa provavelmente não é uma boa opção para o tamanho da chave RSA, porque quebrá-la é uma tarefa relativamente fácil para os invasores. Portanto, se há dez anos, 1000 bits pareciam uma quantidade razoável, hoje, ao criar um sistema, você deve escolher a chave RSA de 2000, 3000 ou mesmo 4000 bits. Portanto, o tamanho da chave RSA significa o tamanho desses números primos.

Então, por conveniência, falaremos sobre o número n, que é simplesmente o produto desses números primos n = pq, e esse número é chamado de módulo. Portanto, agora que sabemos como criar a chave, ou pelo menos parte dela, teremos que descobrir como criptografar e descriptografar as mensagens.



E a maneira como criptografamos e descriptografamos as mensagens se baseia no aumento do poder dos números no módulo n. Parece um pouco estranho, mas vamos descobrir isso em um segundo. Portanto, se você deseja criptografar a mensagem m, deve convertê-la em m ^e pelo mod n. O valor de e é um grau; em um segundo, descobriremos como escolhê-lo. É assim que vamos criptografar a mensagem.

Ou seja, apenas pegamos essa mensagem como um número inteiro e aumentamos para uma potência. Em um segundo, veremos por que isso funciona, mas, por enquanto, denotaremos toda essa mensagem criptografada com a letra C.

Então, para decifrá-lo, precisamos encontrar outro expoente interessante d, que nos permita pegar a mensagem criptografada C, elevá-la à potência d módulo e, como resultado, obter magicamente a mensagem descriptografada m.

Portanto, o princípio geral é usar um expoente para criptografar uma mensagem e outro expoente para descriptografá-la.



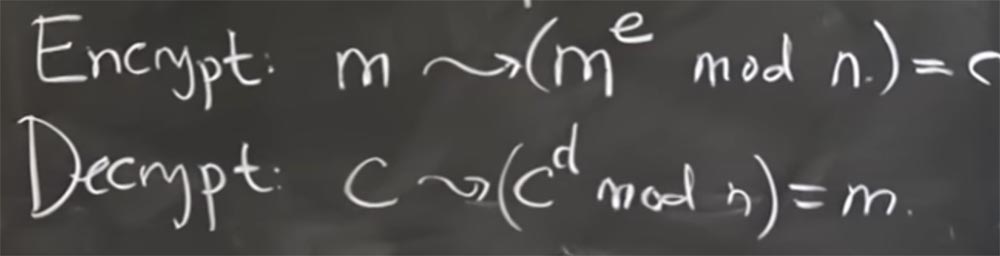
Em suma, parece um pouco difícil entender como vamos apresentar esses dois números mágicos que, de alguma forma, nos devolvem a mensagem original. Mas se você observar como esse módulo n de exponenciação ou multiplicação funciona, você entenderá tudo.

Se pegarmos X e elevá-lo à potência igual à função φ de n, então este será 1 módulo n:

X ^{φ (n)} = 1 mod n

Essa função phi para nossa escolha particular de n é bastante simples; é igual a φ = (p-1) (q-1).
Então, o produto do expoente aberto e, que é maior que 1, mas menor que φ (n), pelo expoente secreto d, será igual a:

ed = ɑφ (n) +1, onde ɑ é uma constante.

Assim, é possível descriptografar corretamente a mensagem, pois existe um algoritmo bastante simples se você souber o valor de φ (n) para calcular d levando em consideração e ou e levando em consideração d.

Público: 1 módulo n não é igual a 1?

Professor: sim, eu cometi um erro aqui, a igualdade deve ser assim:

X ^{φ (n)} _{mod n} = 1 mod n, ou seja, o valor de X no grau da função "fi" de n módulo n é igual ao módulo unidade n.

Isso basicamente significa que, para a RSA, temos que escolher algum valor e, que será nosso valor de criptografia. Então a partir de e vamos gerar d com base na fórmula de = 1 mod φ (n), portanto d = 1 / e mod φ (n).



Existem alguns algoritmos euclidianos que você pode usar efetivamente para esse cálculo. Mas, para fazer isso, você deve saber isso φ (n), que requer fatoração, ou seja, a fatoração do nosso número n nos fatores peq.

Portanto, o RSA é um sistema em que a chave pública é um par: o expoente de criptografia e e o número n, e o par d e n é uma chave privada que é mantida em segredo. Assim, qualquer pessoa pode aumentar o poder de criptografá-lo para você. Mas somente você conhece esse valor de d e, portanto, pode descriptografar a mensagem. E até você conhecer a fatoração desses fatores P e Q, ou N, igual ao produto de P e Q, você não sabe o que φ = (p-1) (q-1) é.



Como resultado, calcular esse valor de d é uma tarefa bastante difícil. É disso que trata o algoritmo RSA de alto nível.

Agora que nos familiarizamos com os princípios da RSA, quero me debruçar sobre duas coisas. Existem truques sobre como usá-lo corretamente e existem armadilhas que surgem ao usá-lo. Existem várias maneiras de implementar código para essa exponenciação e fazê-lo de forma eficiente. Essa é uma tarefa bastante extraordinária, porque estamos lidando com números inteiros de 1000 bits, para os quais você não pode simplesmente executar a instrução de multiplicação. Provavelmente levará muito tempo para concluir essas operações.

Portanto, a primeira coisa que quero mencionar são as várias armadilhas da RSA. Um deles é a multiplicatividade. Suponha que tenhamos 2 mensagens: m ₀ e m ₁ . Vou criptografá-los, transformando m ₀ em m ₀ ^e mod n, e m1 em m ₁ ^e mod n. Um possível problema, ou melhor, não necessariamente um problema, mas uma surpresa desagradável para alguém que usa RSA é que é muito fácil criptografar o produto m ₀ por m ₁ , porque você simplesmente multiplica esses 2 dígitos: m ₀ ^e mod n * m ₁ ^e mod n.



Se você multiplicá-los, você terminará com o produto (m ₀ m ₁ ) ^e módulo n. Esta é a criptografia correta com o uso simplificado do RSA para o valor m ₀ m ₁ . No momento, esse não é um grande problema, porque você pode simplesmente criar essa mensagem criptografada, mas não pode descriptografá-la. No entanto, é possível que um sistema comum permita descriptografar mensagens específicas. Ou seja, se permitir descriptografar a mensagem que você criou, talvez seguindo o caminho inverso, você possa descobrir quais são essas mensagens m ₀ e m ₁ .

Esse fato não deve ser ignorado, pois afeta vários protocolos usando o RSA. Há uma propriedade que usaremos como mecanismo de defesa no final de nossa palestra.

A segunda armadilha, ou propriedade da RSA, à qual você deve prestar atenção é o determinismo ou determinabilidade. Na implementação elementar descrita anteriormente, se você pegar a mensagem me criptografá-la, transformando-a em m ^e mod n, essa é uma função determinística da mensagem. Portanto, se você criptografar novamente, obterá exatamente a mesma criptografia.

Essa não é uma propriedade desejável, porque se vejo que você está enviando alguma mensagem criptografada usando o RSA e quero saber o que é, pode ser difícil descriptografá-la. Mas posso tentar coisas diferentes, pelo que vejo que você está enviando esta mensagem.

Então eu vou criptografá-lo e ver se você obtém o mesmo texto criptografado. E se assim for, então vou descobrir que você criptografou. Porque tudo o que preciso para criptografar uma mensagem é uma chave pública acessível ao público, que é um par de números (n, e).

Portanto, isso não é tão bom e talvez você precise ter cuidado com essa propriedade ao usar o RSA. Assim, é difícil usar primitivos desse tipo diretamente.



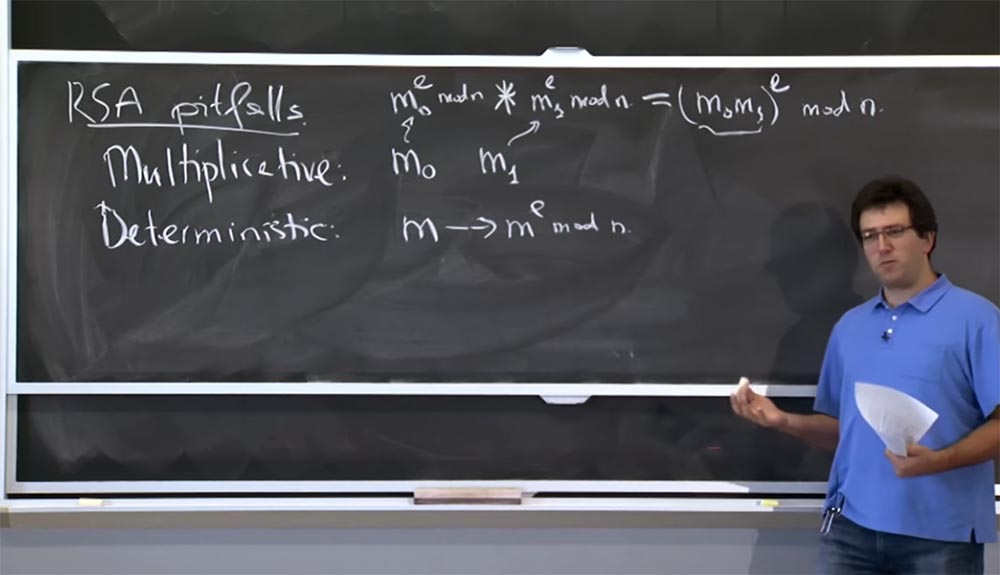
Na prática, para evitar problemas semelhantes com o RSA, as pessoas codificam a mensagem de uma certa maneira antes da criptografia. Em vez de elevar diretamente uma mensagem a um poder, eles pegam algum tipo de função de mensagem e o elevam a um módulo de poder:

(f (m)) ^e mod n.

Essa função f, usada hoje em dia, é chamada OAEP - Criptografia assimétrica ideal com adição. Isso é algo codificado com duas propriedades interessantes.

Em primeiro lugar, traz aleatoriedade. Você pode pensar em f (m) como gerando uma mensagem de 1000 bits que você irá criptografar. Parte desta mensagem será sua mensagem aqui no meio deste retângulo. Obviamente, você pode recuperá-lo ao descriptografar. Portanto, há duas coisas interessantes que você deseja fazer: à direita, você coloca algum tipo de aleatoriedade, o valor de r. Isso significa que, se você criptografar uma mensagem várias vezes, obterá resultados diferentes a cada vez, para que a criptografia não seja mais determinada.

Para superar essa propriedade multiplicativa e outros tipos de problemas, à esquerda você tem um pad pad, que é uma sequência do tipo 1 0 1 0 1 0. Você pode escolher uma sequência melhor, mas, grosso modo, esse é algum tipo de sequência previsível, que você insere aqui e sempre que descriptografa a mensagem, verifique se essa sequência ainda está lá. A multiplicidade destruirá esses bits, e então ficará claro para você que alguém estragou sua mensagem e a descartou. Se esses bits permanecerem no lugar, isso prova que ninguém falsificou sua mensagem e você pode recebê-la, pois ela foi criptografada corretamente por alguém.



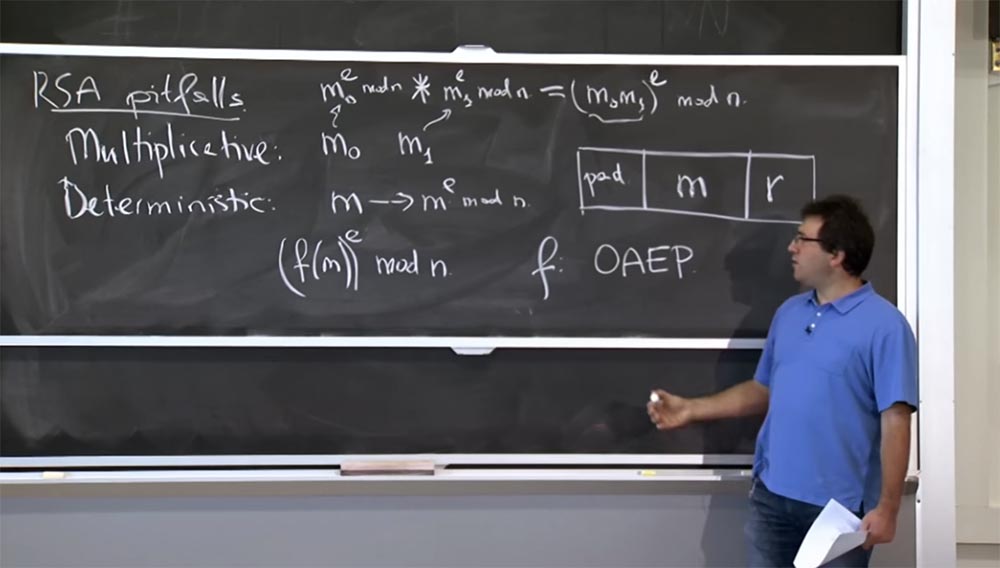Público: se um invasor sabe qual é o valor do bloco, ele pode definir 1 no final da sequência e multiplicar esse valor?

Professor: sim, talvez. Isso é um pouco complicado, porque essa aleatoriedade r continuará. Portanto, o design específico desta OAEP é um pouco mais complicado do que o que descrevi. Mas imagine que se trata de uma multiplicação inteira e não bit a bit, a aleatoriedade se estende ainda mais, para que você possa criar um esquema OAEP no qual isso não acontecerá.

Acontece que você não deve usar essa matemática RSA diretamente, na prática, você deve usar algum tipo de biblioteca que implemente todas essas coisas para você da maneira correta e use-a como um parâmetro de criptografia e descriptografia.

No entanto, os detalhes discutidos acima serão importantes para nós, pois estamos realmente tentando descobrir como interromper ou atacar a implementação existente do RSA.

Em particular, o ataque descrito no artigo da palestra aproveitará o fato de o servidor estar prestes a testar esse complemento de preenchimento quando receber a mensagem. Portanto, é assim que consideraremos o tempo que levará para o servidor descriptografar. Vamos enviar uma mensagem cuidadosamente construída, mas ela não é criada a partir da mensagem real me de sua criptografia. Vamos criar um valor inteiro criptografado completo.

O servidor tentará descriptografá-lo e obterá algum tipo de absurdo, com o qual o teclado provavelmente não será emparelhado, e o servidor rejeitará imediatamente essa mensagem. , , , , : RSA, , . , . , .

, , RSA. , , , . , , , 1000 . e .



, . , 1000 . 1000- , 1000 1000 n, . RSA , .
4 , . , . , CRT. . . , , , , [ = a ₁ ] mod p [ = a ₂ ] mod q, q – , .



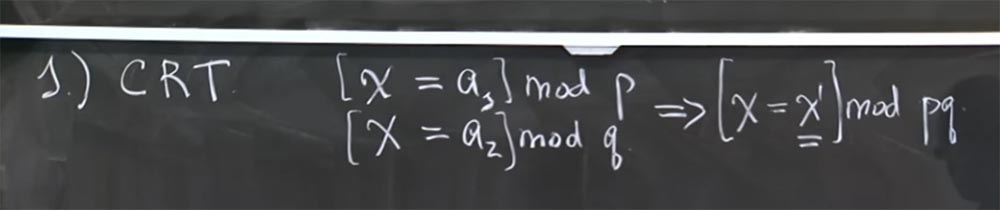
, [ = ¹ ] mod pq. ¹ , . ¹ , mod pq a ₁ a ₂ mod p q.

, ? , , n, p q.



, mod pq, mod p mod q. , , mod pq. , ? , , ?

: , ?

: , , , . , p q, n 1000 , p q 500 , . , , — , , . — . , , . 1000 512 , 2 . , 4 . [ = a ₁ ] mod p [ = a ₂ ] mod q , 4 . 2 RSA , .

, .

, Sliding windows, « ». . , .



, - , 500 , mod p mod q, d. c d? , c d . d , 500, . , , . , « ». .

c ^2x , : (c ^x ) ² :

c ^2x = (c ^x ) ²

c ^2x , 2 , cx, . , , c ^2x+1 :

c ^2x+1 = (c ^x ) ² x

.

, , , . , , , . , .

« », ? , . , , « » c ^2x+1 = (c ^x ) ² x .

, , , – , c ^2x+1 c ^2x , c. , , . , .



, :

1
3
7
...
31

. , , , .

, ^32x+y , 5 , 32- , ^y .



³² . , , , , c . «» .

29:00

Curso MIT "Segurança de sistemas de computadores". Aula 16: Ataques pelo canal lateral, parte 2


A versão completa do curso está disponível aqui .

Obrigado por ficar conosco. Você gosta dos nossos artigos? Deseja ver materiais mais interessantes? Ajude-nos fazendo um pedido ou recomendando a seus amigos, um desconto de 30% para os usuários da Habr em um análogo exclusivo de servidores básicos que inventamos para você: Toda a verdade sobre o VPS (KVM) E5-2650 v4 (6 núcleos) 10GB DDR4 240GB SSD 1Gbps de US $ 20 ou como dividir o servidor? (as opções estão disponíveis com RAID1 e RAID10, até 24 núcleos e até 40GB DDR4).

VPS (KVM) E5-2650 v4 (6 núcleos) 10 GB DDR4 240 GB SSD de 1 Gbps até dezembro de graça quando pagar por um período de seis meses, você pode fazer o pedido aqui .

Dell R730xd 2 vezes mais barato? Somente nós temos 2 TVs Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 a partir de US $ 249 na Holanda e nos EUA! Leia sobre Como criar um prédio de infraestrutura. classe usando servidores Dell R730xd E5-2650 v4 custando 9.000 euros por um centavo?