Curso MIT "Segurança de sistemas de computadores". Aula 16: Ataques pelo canal lateral, parte 2

Instituto de Tecnologia de Massachusetts. Curso de Aula nº 6.858. "Segurança de sistemas de computador". Nikolai Zeldovich, James Mickens. 2014 ano

Computer Systems Security é um curso sobre o desenvolvimento e implementação de sistemas de computador seguros. As palestras abrangem modelos de ameaças, ataques que comprometem a segurança e técnicas de segurança baseadas em trabalhos científicos recentes. Os tópicos incluem segurança do sistema operacional (SO), recursos, gerenciamento de fluxo de informações, segurança de idiomas, protocolos de rede, segurança de hardware e segurança de aplicativos da web.

Palestra 1: “Introdução: modelos de ameaças” Parte 1 / Parte 2 / Parte 3
Palestra 2: “Controle de ataques de hackers” Parte 1 / Parte 2 / Parte 3
Aula 3: “Estouros de Buffer: Explorações e Proteção” Parte 1 / Parte 2 / Parte 3
Palestra 4: “Separação de Privilégios” Parte 1 / Parte 2 / Parte 3
Palestra 5: “De onde vêm os sistemas de segurança?” Parte 1 / Parte 2
Palestra 6: “Oportunidades” Parte 1 / Parte 2 / Parte 3
Palestra 7: “Sandbox do Cliente Nativo” Parte 1 / Parte 2 / Parte 3
Aula 8: “Modelo de Segurança de Rede” Parte 1 / Parte 2 / Parte 3
Aula 9: “Segurança de aplicativos da Web” Parte 1 / Parte 2 / Parte 3
Palestra 10: “Execução Simbólica” Parte 1 / Parte 2 / Parte 3
Aula 11: “Linguagem de Programação Ur / Web” Parte 1 / Parte 2 / Parte 3
Aula 12: Segurança de rede Parte 1 / Parte 2 / Parte 3
Aula 13: “Protocolos de Rede” Parte 1 / Parte 2 / Parte 3
Palestra 14: “SSL e HTTPS” Parte 1 / Parte 2 / Parte 3
Palestra 15: “Software Médico” Parte 1 / Parte 2 / Parte 3
Palestra 16: “Ataques de Canal Lateral” Parte 1 / Parte 2 / Parte 3

Público: como determinar xey primeiro?

Professor: para isso, você deve olhar o expositor em representação binária. Suponha que eu tente calcular o valor de c ^1011010 , o grau também pode consistir em um número maior de bits. Se queremos fazer um re-quadrado, precisamos olhar para o bit mais baixo - aqui está 0.



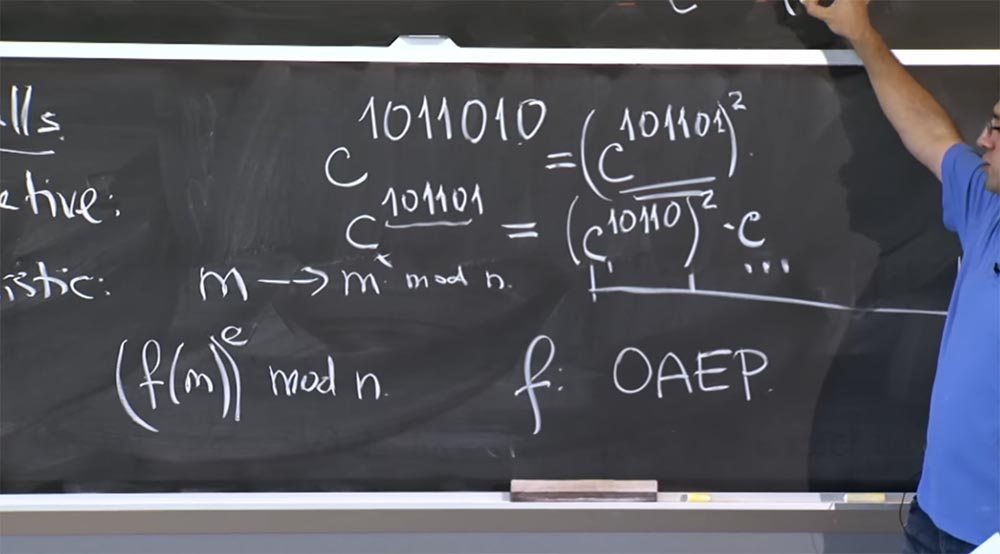
Assim, obtemos a igualdade c ^1011010 = (c ¹⁰¹¹⁰¹ ) ²

Em seguida, precisamos calcular c ¹⁰¹¹⁰¹ , aqui não podemos usar esta regra, porque ela não é 2x - será x mais 1. Portanto, escrevemos esta igualdade:

c ¹⁰¹¹⁰¹ = (c ¹⁰¹¹⁰ ) ² c, porque esse prefixo 101101 = 10110 + 1.

Portanto, multiplicamos o quadrado por c, então o usamos para re-quadrado.

Para "janelas deslizantes", precisamos capturar mais bits da extremidade inferior. Se você quiser fazer um truque aqui com uma “janela deslizante” em vez de extrair um s daqui, levando em conta essa tabela enorme, podemos levar 3 bits de cada vez, agarrando-nos a c7. Se tomarmos os 3 primeiros bits de um grau, obtemos c ¹⁰¹¹⁰¹ = (c ¹⁰¹ ) ⁸ c ¹⁰¹ .

Nesse caso, temos realmente a mesma quantidade de cálculos para (c ¹⁰¹ ) ⁸ , mas você pode ver o valor de c ¹⁰¹ na tabela. E a parte na forma de (c ¹⁰¹ ) ⁸ diz que você usará "janelas deslizantes" para calcular seu valor.



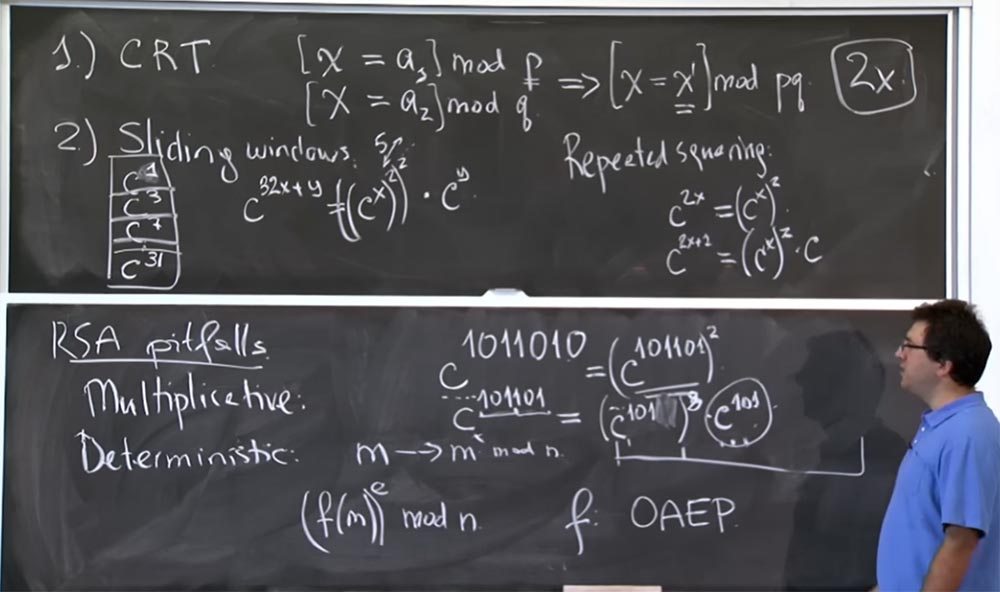
Isso economiza muito tempo, pois possibilita o uso de valores pré-multiplicados. Há 10 anos, acreditava-se que uma tabela de valores de até 32 graus é o plano ideal em termos de eficiência computacional, porque existe algum tipo de compromisso aqui, certo? Você gasta tempo criando essa tabela, mas ela não deve ser muito grande se você não usar alguns registros com frequência. Suponha que, se você criar uma tabela de valores até c ⁵⁰⁰ graus, mas não usará expoentes com um valor maior que 128, apenas perca seu tempo.

Público: existe algum motivo para não criar uma mesa tão gigante com antecedência? Ou seja, para calcular os valores de um número limitado de graus que podem ser contornados nos cálculos?

Professor: se você não deseja realizar cálculos volumétricos com antecedência ... bem, há duas coisas. Uma é que você deve ter um código para verificar se o registro necessário na tabela está cheio ou não, e isso provavelmente reduzirá a precisão de prever as ramificações dos processos da CPU. Ao mesmo tempo, no caso geral, o processador funcionará mais lentamente, pois precisará verificar se o registro necessário está na tabela. A segunda coisa, que é um pouco irritante, pode ser o vazamento de entradas da tabela por vários canais laterais, nomeadamente através de padrões de acesso ao cache. Portanto, se você tiver algum outro processo em execução no mesmo processador, poderá ver quais endereços de cache foram removidos ou mais lentos porque alguém tem acesso ao registro c ³ ou ao registro c ³¹ . E quanto maior essa tabela, mais fácil é determinar quais bits do expoente são usados ​​para criar a chave RSA.

Essa tabela gigante é capaz de dizer qual endereço de cache foi perdido para o processador, ou seja, indica que o processo de criptografia deve ter acesso a essa entrada na tabela. Por sua vez, isso informa que a sequência de bits especificada aparece no expoente da sua chave privada. Portanto, suponho que matematicamente você possa preencher esta tabela o quanto for necessário, mas na prática você não deseja que ela seja de tamanho gigantesco. Além disso, você não poderá usar efetivamente grandes entradas de tabela. É muito mais útil usar os registros de uma tabela relativamente pequena repetidamente, por exemplo, para calcular c ^7, você pode usar o valor c ³ duas vezes e assim por diante.

Então, aqui está a otimização do RSA, re-esquadrando e métodos de "janela deslizante". Não sei se eles ainda usam esse tamanho de "janelas deslizantes", mas, de qualquer forma, isso acelera o processo de cálculo, porque, caso contrário, você teria que quadrado cada bit do expoente e multiplicar por cada bit. Portanto, se você tiver um expoente de 500 bits, precisará completar 500 quadrados e aproximadamente 256 multiplicações por c. Com as “janelas deslizantes”, você ainda precisa fazer 512 quadrados, porque isso não pode ser evitado, mas o número de multiplicações por c diminuirá de 256 para cerca de 32 devido ao uso de entradas da tabela.

Este é o plano geral de otimização, que acelera o processo de cálculo cerca de uma vez e meia. Essa é uma otimização bastante simples. Existem dois truques inteligentes com números que tornam o processo de multiplicação mais eficiente.

A primeira é a transformação de Montgomery, em um segundo veremos por que isso é especialmente importante para nós. Essa otimização está tentando resolver um problema para nós, ou seja, toda vez que fazemos a multiplicação, obtemos um número que continua a crescer e a crescer em ordem crescente. Em particular, tanto nas "janelas deslizantes" quanto nas re-quadradas, você realmente multiplicou dois números juntos quando elevou c à potência de y.

O problema é que, se os dados de entrada c ^x e ^y para multiplicação fossem, digamos, 512 bits cada, o tamanho do resultado da multiplicação seria de 1000 bits. Depois disso, você pega esse resultado de 1000 bits e o multiplica novamente por algo como 512 bits, torna-se o tamanho de 1500, 2000, 2500 bits e tudo cresce e cresce.

No entanto, você não deseja isso, porque a multiplicação aumenta a ordem dos números multiplicados. Por isso, devemos manter nosso tamanho numérico o menor possível, basicamente igual a 512 bits, porque todos esses cálculos são mod p ou mod q.

Podemos reduzir esse número, digamos, queremos calcular ((( ^x ) ² ) ² ) ² ) ² . O que você pode fazer é, por exemplo, calcular cx módulo p, depois ao quadrado novamente módulo p e mais uma vez ao quadrado módulo p. Esse método é relativamente bom, porque nos permite manter o tamanho do nosso número dentro de 512 bits, ou seja, o menor possível. Isso é bom no sentido de reduzir o tamanho dos números que precisamos multiplicar, mas, de fato, a operação com este módulo p "aumenta significativamente o custo" do cálculo.



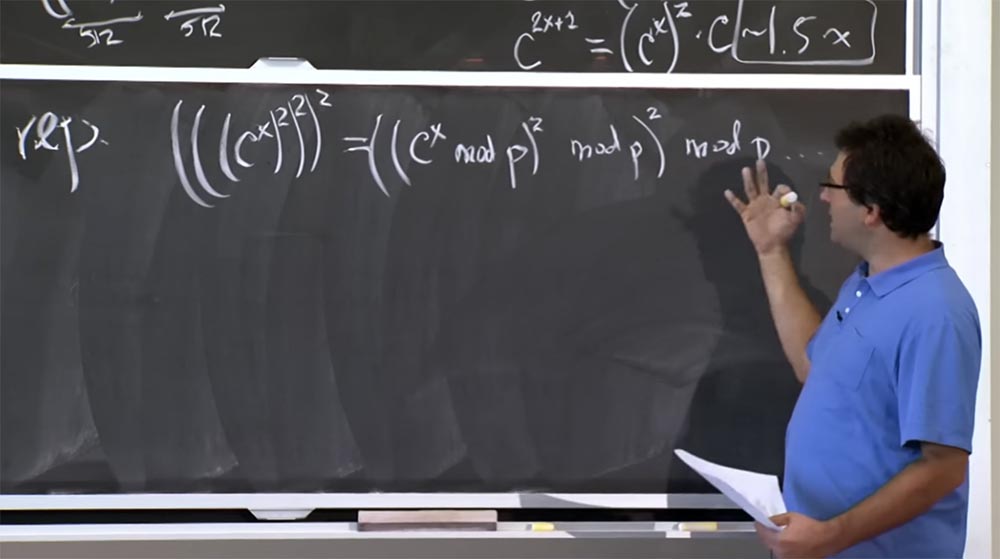
Porque a maneira como você obtém o mod p está em divisão. E divisão é pior que multiplicação. Não listarei os algoritmos para divisão, mas é muito lento. Geralmente, você tenta evitar operações de divisão sempre que possível, porque isso não é uma programação fácil. O fato é que você precisa usar algum tipo de algoritmo de aproximação, métodos de Newton e similares, e tudo isso desacelerará o processo de cálculo.

A multiplicação é muito mais lucrativa, mas o uso de operações mod p ou mod q para reduzir o tamanho dos números custará mais que a multiplicação. Mostrarei uma maneira de evitar isso e como fazer cálculos rápidos usando a transformação Montgomery.

A idéia básica é representar os números inteiros que você irá multiplicar na forma de uma transformação de Montgomery. Isso é realmente muito fácil. Para fazer isso, simplesmente multiplicamos nosso número a por um certo valor mágico R. Depois de um segundo, vou lhe dizer o que é. Mas vamos primeiro descobrir o que acontece quando selecionamos um valor arbitrário de R.

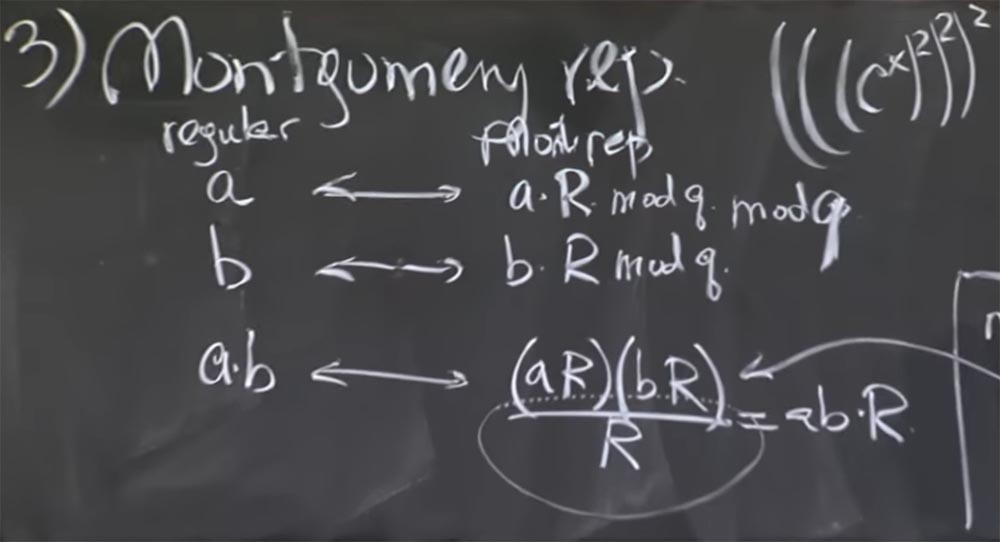
Portanto, pegamos 2 números, aeb, e os convertemos para a representação de Montgomery, multiplicando cada um por R. Em seguida, o produto de aeb na transformação de Montgomery terá a seguinte aparência:

ab <-> (aR) (bR) / R = abR

Ou seja, você multiplica aR por bR e obtém o produto de ab por R ao quadrado. Agora, temos dois Rs, isso é um pouco chato, mas você pode dividi-lo por R. Como resultado, obtemos o produto de ab por R. Não está claro por que precisamos multiplicar esse número novamente. Vamos primeiro descobrir se isso está correto e depois entenderemos por que será mais rápido.
Isso está correto no sentido de que é muito fácil. Se você deseja multiplicar alguns números, é necessário multiplicá-los por esse valor de R e obter a transformação Montgomery. Cada vez que multiplicamos esses 2 números, devemos dividi-los por R e depois observar a forma resultante da transformação da forma abR. Então, quando terminarmos o quadrado, a multiplicação e todas essas coisas, retornaremos à forma normal e comum do resultado, simplesmente dividindo por R pela última vez.



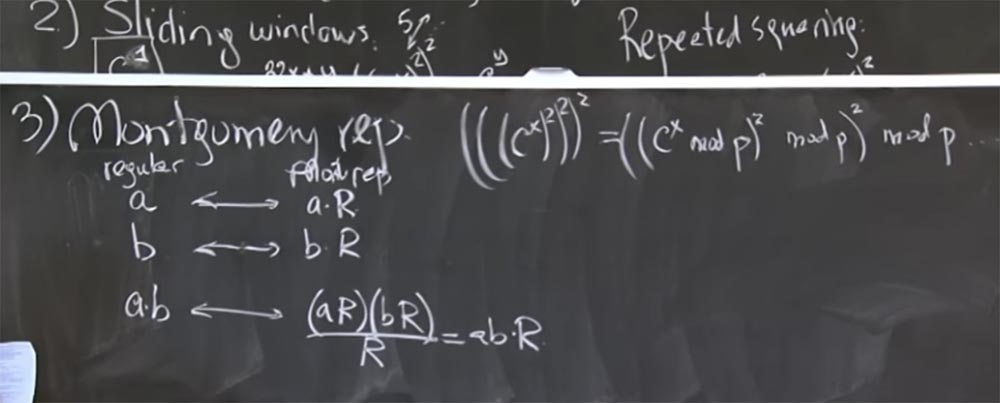
Agora considere como escolher o número mais adequado para R, para tornar a divisão por R uma operação muito rápida. E o mais legal aqui é que, se a divisão por R é muito rápida quando é um número pequeno, e não precisamos fazer esse mod q com muita frequência. Em particular, aR, digamos, também terá um tamanho de cerca de 500 bits, porque tudo isso é na verdade mod p ou mod q. Assim, aR é de 500 bits, bR também será de 500 bits, de modo que o produto (aR) (bR) será de 1000 bits. R também será um número conveniente de 500 bits, do tamanho de p. E se pudermos tornar a operação de divisão rápida o suficiente, o resultado de ab também será de aproximadamente um número de 500 bits, para que possamos multiplicar sem a necessidade de divisão adicional. Dividir por R é muito mais rentável e nos dá um pequeno resultado, o que evita o uso de mod p na maioria das situações.

Então, qual é esse número estranho de R que eu estou falando o tempo todo? Tem um valor de 2 a 512 graus:

R = 2 ⁵¹²

Será 1 e um monte de zeros, então é fácil multiplicar por esse número, porque basta adicionar um monte de zeros ao resultado. A divisão também pode ser simples se os bits menos significativos do resultado forem zero. Portanto, se você tiver um valor de uma pilha de bits acompanhados de 512 zeros, dividir por 2 a 512 graus será muito simples - basta soltar zeros no lado direito, e esta é uma operação de divisão completamente correta.

O pequeno problema é que, na verdade, não temos zeros no lado direito quando você faz essa multiplicação. Temos números reais de 512 bits usando todos os 512 bits.

O produto de (aR) por (bR) também é um número real da ordem de 1000 bits, portanto, não podemos simplesmente eliminar os bits menos significativos. Mas uma abordagem razoável é baseada no fato de que a única coisa que nos preocupa é o valor do mod p. Assim, você sempre pode adicionar vários p a esse valor sem alterar seu equivalente em mod p. Como resultado, podemos adicionar múltiplos valores de p para que todos os bits menos significativos se tornem zeros. Vejamos alguns exemplos simples. Não vou escrever 512 bits no quadro, mas vou dar apenas um pequeno exemplo.

Suponha que em nossa situação R = 2 ⁴ = 10000. Este é um tamanho muito menor do que realmente é. Vamos ver como essa transformação de Montgomery funciona. Tentamos calcular o mod q, onde q = 7. Em forma binária, q = 7 é (111).

Suponha ainda que realizamos alguma multiplicação (aR) (bR) e, na representação binária, o resultado é 11010, ou seja, esse será o valor do produto (aR) (bR). Como a dividimos por R?

Obviamente, nem todos os quatro bits menos significativos são zeros; portanto, não podemos apenas separá-los, mas podemos adicionar quantidades que são múltiplos de q. Em particular, podemos adicionar 2 vezes em q, com 2q = 1110 na representação binária. Como resultado, temos 101000, espero ter feito tudo certo.



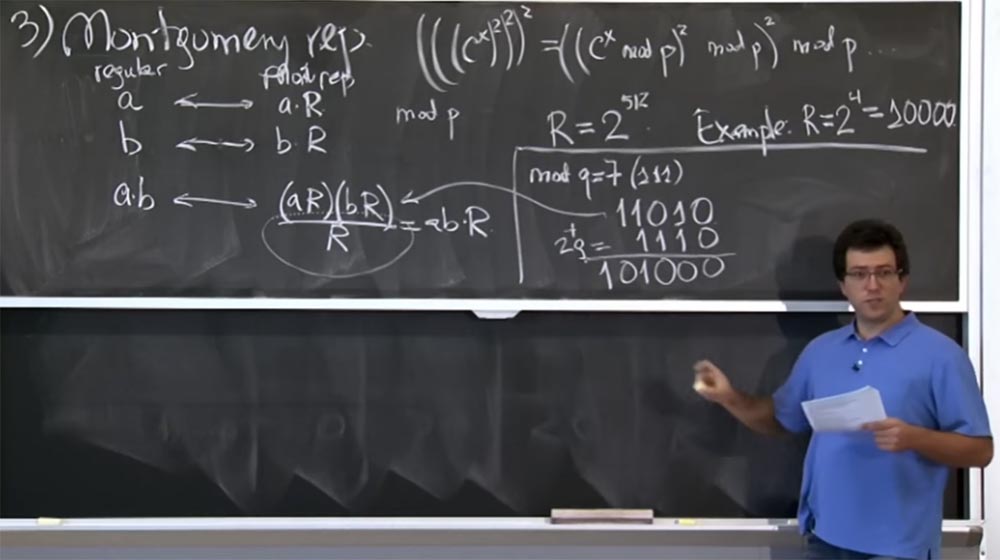
Então temos a soma (aR) (bR) + 2q. Na verdade, não nos importamos com + 2q, porque só nos preocupamos com o valor do mod q. Agora estamos mais perto da meta, porque temos três zeros à direita. Agora podemos adicionar um pouco mais de q. Digamos que desta vez será 8q, que é 111000. Novamente, adicione nossas linhas e obtenha 1100000. Agora temos o original (aR) (bR) + 2q + 8q = 1100000. Finalmente, podemos facilmente dividir essa coisa em R, apenas soltando quatro zeros baixos.



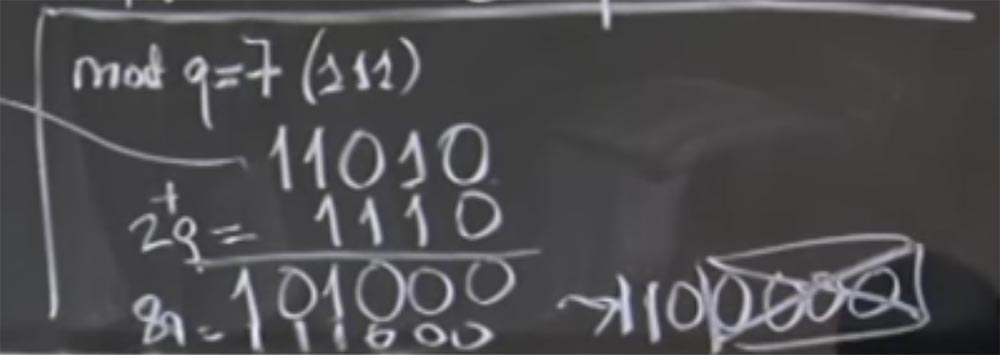Público: produto (aR) (bR) sempre terminará com 1024 zeros?

Professor: não, e vou explicar o que poderia ser a confusão. Digamos que o número a seja 512 bits, multiplicamos por R e obtivemos um número de 1000 bits. Nesse caso, você está certo, aR é o número em que os bits altos são a e os bits baixos são todos zeros. Mas então executamos o mod q para torná-lo menor. Portanto, o tamanho de 1024 bits geralmente é uma coincidência, pois esse número tem esses zeros baixos apenas durante a primeira conversão, mas depois de fazer algumas multiplicações, serão bits arbitrários.

Para não enganá-lo, tive que escrever mod q aqui após aR e após bR - aqui estou adicionando - e calcular esse mod q assim que você fizer a conversão para reduzir o valor.



A conversão inicial é bastante trabalhosa, ou pelo menos tão cara quanto a modulação convencional na multiplicação. O legal é que você paga esse preço uma vez ao fazer a conversão de Montgomery e, em vez de convertê-lo novamente em cada etapa dos cálculos, basta mantê-lo na forma de uma exibição de Montgomery.
Lembre-se de que para aumentar para uma potência que tem 512 bits, você terá que fazer mais de 500 multiplicações, porque temos que fazer pelo menos 500 quadrados e um pouco mais. Então você mod q duas vezes e, em seguida, realiza muitas operações de divisão simples, se permanecer nesta forma de representar números. E no final, você faz uma divisão por R para retornar a esse formulário ab.

Então, em vez de fazer o mod q 500 vezes para cada etapa da multiplicação, você mod q duas vezes e depois continua fazendo essas divisões por R a um custo mínimo.
Público: quando você adiciona múltiplos de q e depois divide por R, temos um restante?
Professor: na verdade, mod q significa o restante quando você divide por q. Simplificando, x + yq mod q = x. Nesse caso, há outra propriedade útil - que todos os módulos são primos. Isso é tão verdadeiro quanto o fato de que se você tem (x + yq / R) mod q, então é igual a x / R mod q.



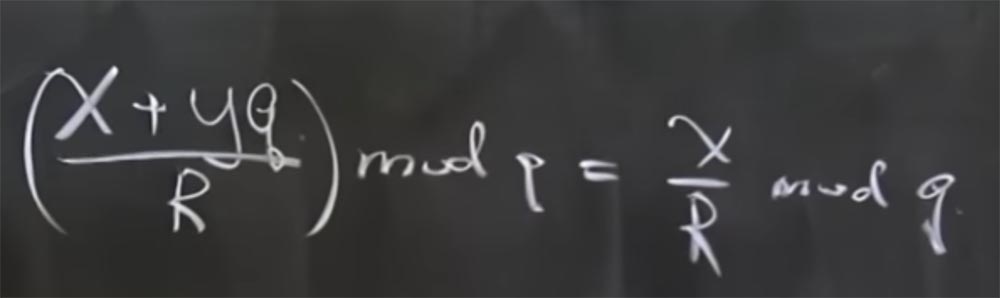
A razão para pensar assim é que não há operações reais de divisão na aritmética modular, é apenas inversão. De fato, isso significa que, se multiplicarmos (x + yq) por R invertido calculado pelo mod q, é igual à soma de dois produtos: o produto x do R invertido pelo mod q e o produto de yq pelo R invertido pelo mod q. Além disso, o último termo é reduzido, porque é algo multiplicado por q.



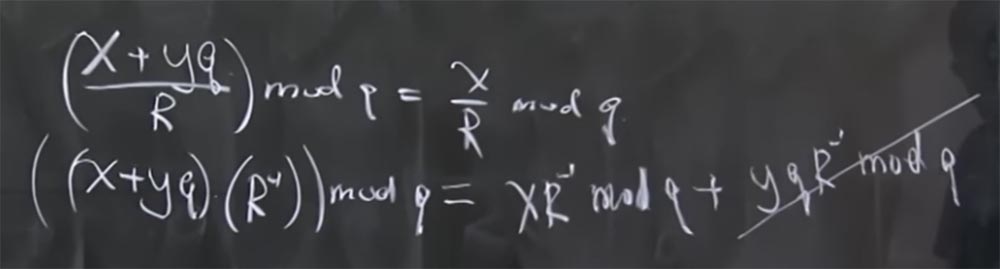
Para coisas como somar 2q, 8q e assim por diante, existe uma fórmula que acelera o processo de cálculo. Fiz isso gradualmente, primeiro calculei 2q, depois 8q e assim por diante, mas o material da palestra tem uma fórmula completa que pode ser usada, só que não quero perder tempo escrevendo no quadro. Permite calcular o valor múltiplo de q que você deve adicionar para que todos os bits menos significativos se transformem em 0. Então, para fazer a divisão por R, você só precisa calcular esse múltiplo mágico de q, adicioná-lo e descartar o valor baixo. zero bits, e isso retornará seu número para 512 bits, independentemente do tamanho do resultado obtido.

Mas há uma sutileza. A única razão pela qual estamos falando disso é porque algo engraçado está acontecendo aqui, o que nos permite descobrir informações sobre os horários. Em particular, embora tenhamos dividido por R, ainda sabemos que o resultado será de cerca de 512 bits. Mas ainda pode ser maior que q, porque q não é um número de 512 bits, pode ser um pouco menor que R.

Assim, pode ser que, depois de fazermos essa divisão vantajosa por R, talvez seja necessário subtrair q novamente, porque obtemos algo pequeno, mas ainda não pequeno o suficiente. Portanto, há uma chance de que, após essa divisão, possamos subtrair q novamente. E essa subtração pode ser usada como parte do ataque, porque a operação de subtração adiciona o tempo de cálculo.



E alguém descobriu - não esses caras, mas alguém no trabalho anterior - que há uma chance de fazer algo chamado redução extra ou redução adicional. , . , xd mod q, - x mod q, 2R. .



, x mod q , . , cd.



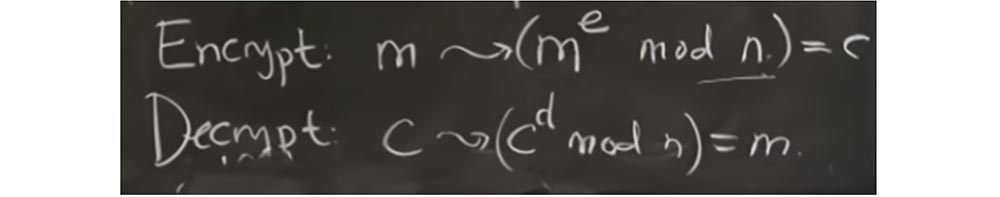
, extra reduction , X , , , q.



, c, extra reduction , c — q. , , q . , extra reduction, , , X mod q , = q + έ, . , . , , , , extra reduction .

: , ?

: , extra reduction? , , , . , . , , extra reduction, , , . , . , , mod q. , , , . , mod q , , .

, . , - , . — , . , - , extra reduction .

, . , OpenSSL, , . , mod q . , , .

, , , , a b. — 512- . , 32- , , 64- ? ?



- ? , , a b .

, , 512 , 64- , 32- . a : a ₁ a ₀ , a ₀ , a ₁ — . b – b ₁ b ₀ .

ab 3- : a ₁ b ₁ , a ₀ b ₀ , a ₁ b ₀ + a ₀ b ₁ . .



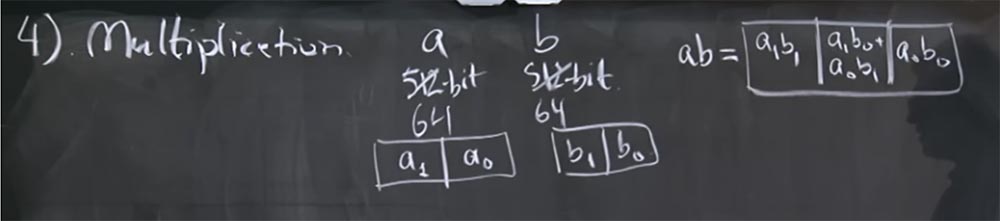
55:00

Curso MIT "Segurança de sistemas de computadores". 16: « », 3


A versão completa do curso está disponível aqui .

Obrigado por ficar conosco. Você gosta dos nossos artigos? Deseja ver materiais mais interessantes? Ajude-nos fazendo um pedido ou recomendando a seus amigos, um desconto de 30% para os usuários da Habr em um análogo exclusivo de servidores básicos que inventamos para você: Toda a verdade sobre o VPS (KVM) E5-2650 v4 (6 núcleos) 10GB DDR4 240GB SSD 1Gbps de US $ 20 ou como dividir o servidor? (as opções estão disponíveis com RAID1 e RAID10, até 24 núcleos e até 40GB DDR4).

VPS (KVM) E5-2650 v4 (6 núcleos) 10 GB DDR4 240 GB SSD de 1 Gbps até dezembro de graça quando pagar por um período de seis meses, você pode fazer o pedido aqui .

Dell R730xd 2 vezes mais barato? Somente nós temos 2 TVs Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 a partir de US $ 249 na Holanda e nos EUA! Leia sobre Como criar um prédio de infraestrutura. classe usando servidores Dell R730xd E5-2650 v4 custando 9.000 euros por um centavo?