Curso MIT "Segurança de sistemas de computadores". Palestra 16: “Ataques de Canal Lateral”, Parte 3

Instituto de Tecnologia de Massachusetts. Curso de Aula nº 6.858. "Segurança de sistemas de computador". Nikolai Zeldovich, James Mickens. 2014 ano

Computer Systems Security é um curso sobre o desenvolvimento e implementação de sistemas de computador seguros. As palestras abrangem modelos de ameaças, ataques que comprometem a segurança e técnicas de segurança baseadas em trabalhos científicos recentes. Os tópicos incluem segurança do sistema operacional (SO), recursos, gerenciamento de fluxo de informações, segurança de idiomas, protocolos de rede, segurança de hardware e segurança de aplicativos da web.

Palestra 1: “Introdução: modelos de ameaças” Parte 1 / Parte 2 / Parte 3
Palestra 2: “Controle de ataques de hackers” Parte 1 / Parte 2 / Parte 3
Aula 3: “Estouros de Buffer: Explorações e Proteção” Parte 1 / Parte 2 / Parte 3
Palestra 4: “Separação de Privilégios” Parte 1 / Parte 2 / Parte 3
Palestra 5: “De onde vêm os sistemas de segurança?” Parte 1 / Parte 2
Palestra 6: “Oportunidades” Parte 1 / Parte 2 / Parte 3
Palestra 7: “Sandbox do Cliente Nativo” Parte 1 / Parte 2 / Parte 3
Aula 8: “Modelo de Segurança de Rede” Parte 1 / Parte 2 / Parte 3
Aula 9: “Segurança de aplicativos da Web” Parte 1 / Parte 2 / Parte 3
Palestra 10: “Execução Simbólica” Parte 1 / Parte 2 / Parte 3
Aula 11: “Linguagem de Programação Ur / Web” Parte 1 / Parte 2 / Parte 3
Aula 12: Segurança de rede Parte 1 / Parte 2 / Parte 3
Aula 13: “Protocolos de Rede” Parte 1 / Parte 2 / Parte 3
Palestra 14: “SSL e HTTPS” Parte 1 / Parte 2 / Parte 3
Palestra 15: “Software Médico” Parte 1 / Parte 2 / Parte 3
Palestra 16: “Ataques de Canal Lateral” Parte 1 / Parte 2 / Parte 3

Público: Você usa o método Karatsuba?

Professor: Sim, este é um método de multiplicação inteligente que não requer quatro estágios de computação. O método Karatsuba é ensinado no curso .601, ou como é designado hoje?

Audiência: 042.

Professor: 042, excelente. Sim, este é um método muito bom. Quase todas as bibliotecas criptográficas a utilizam. Para aqueles que não são graduados em nosso instituto - digo isso porque temos estudantes aqui - escreverei sobre o método Karatsuba no quadro. Aqui você precisa calcular três valores:

a ₁ b ₁
(a ₁ - a ₀ ) (b ₁ - b ₀ )
a ₀ b ₀

Assim, você faz 3 multiplicações em vez de quatro, e pode restaurar esse valor a ₁ b ₀ + a ₀ b _{1 a} partir desses três resultados de multiplicação.



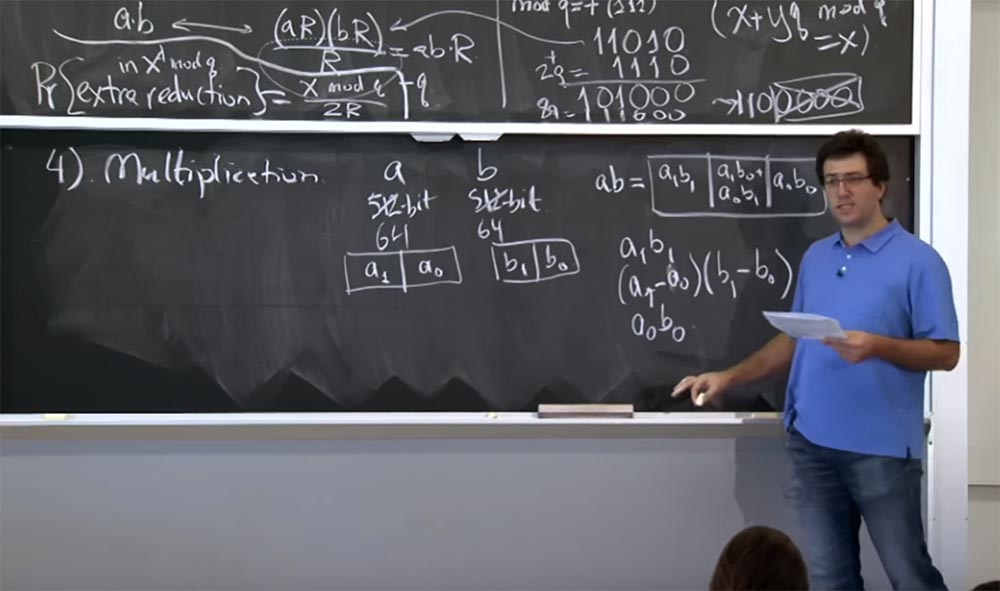
A maneira especial de fazer isso é isso ... deixe-me colocar de uma forma diferente.

Então, teremos:

(2 ⁶⁴ + 2 ³² ) (a ₁ b ₁ ) +
(2 ³² ) (- (a ₁ - a ₀ ) (b ₁ - b ₀ )
(2 ³² + 1) (a ₀ b ₀ )

Isso não está muito claro, mas se você descobrir os detalhes, acabe se convencendo de que esse valor nessas três linhas é equivalente ao valor de ab, mas ao mesmo tempo reduz o cálculo em uma multiplicação. E a maneira como aplicamos isso a multiplicações mais volumosas é que você recursivamente continua diminuindo. Portanto, se você tiver valores de 512 bits, poderá dividi-los na multiplicação de 256 bits. Você faz três multiplicações de 256 bits, cada vez recursivamente, usando o método Karatsuba. No final, seus cálculos se resumem ao tamanho da máquina e podem ser processados ​​por uma única instrução da máquina.



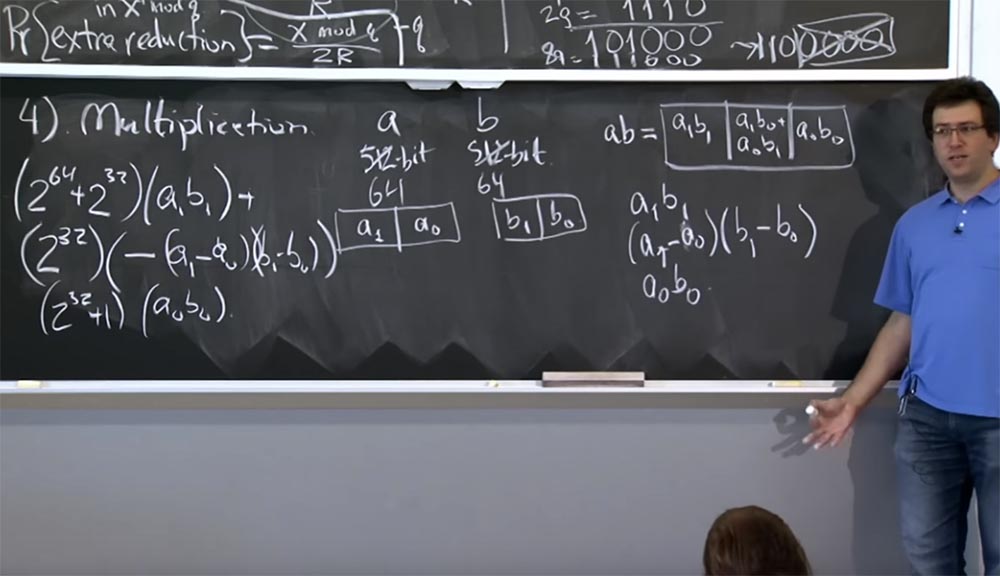
Então, onde está o ataque de tempo? Como esses caras usam a multiplicação de Karatsuba? Acontece que o OpenSSL está preocupado com dois tipos de multiplicação que você pode precisar fazer.
O primeiro é a multiplicação de dois grandes números aproximadamente do mesmo tamanho. Isso acontece muitas vezes quando executamos uma exponenciação modular, porque todos os valores que multiplicaremos terão um tamanho de aproximadamente 512 bits. Portanto, quando multiplicamos c por y ou quadrado, multiplicamos duas coisas aproximadamente do mesmo tamanho. Nesse caso, o método Karatsuba faz muito sentido, porque reduz o tamanho dos números ao quadrado em cerca de 1,58 vezes, o que acelera bastante o processo de cálculo.
O segundo tipo de multiplicação ocorre quando o OpenSSL multiplica dois números cujo tamanho difere significativamente um do outro: um é muito grande e o outro é muito pequeno. Nesse caso, você também pode usar o método Karatsuba, mas ele funcionará mais lentamente que a multiplicação primitiva. Suponha que você multiplique um número de 512 bits por um número de 64 bits, você precisará aumentar cada bit do primeiro número para uma potência de 64, resultando em uma desaceleração do processo 2n em vez da aceleração n / 1,58. Portanto, esses caras que usam o OpenSSL tentaram ser mais inteligentes, e foi aqui que os problemas começaram.

Eles decidiram que alternariam dinamicamente entre o método eficaz de Karatsuba e o método de multiplicação da escola primária. A heurística deles era a seguinte. Se os dois números multiplicados consistirem no mesmo número de palavras-máquina, ou pelo menos tiverem o mesmo número de bits que as unidades de 32 bits, será utilizado o método Karatsuba. Se dois números diferem muito em tamanho um do outro, quadrado ou direto direto, é realizada a multiplicação normal.

Nesse caso, você pode acompanhar como ocorre a mudança para outro método de multiplicação. Como o momento da troca não passa sem deixar vestígios, será perceptível se agora exige muito mais tempo para multiplicação ou muito menos do que antes. Os pesquisadores aproveitaram essa circunstância para organizar um ataque usando o método de temporização.

Acho que terminei de lhe contar todos os truques estranhos que as pessoas usam ao implementar o RSA na prática. Agora vamos tentar reuni-los e usá-los em relação a todo o servidor da Web para descobrir como você pode "extrair" os bits de interesse do pacote de rede de entrada.

Se você se lembra da palestra sobre HTTPS, o servidor da Web possui uma chave secreta. Ele usa essa chave secreta para provar que é o proprietário correto de todos os certificados através de HTTPS ou TLS. Isso ocorre porque os clientes enviam alguns bits selecionados aleatoriamente, esses bits são criptografados usando a chave pública do servidor e o servidor descriptografa essa mensagem usando o protocolo TLS. E se a mensagem estiver marcada, esses bits aleatórios serão usados ​​para estabelecer uma sessão de comunicação.

Mas, no nosso caso, essa mensagem não será verificada, porque será criada de uma maneira especial e, quando os bits extras não corresponderem, o servidor retornará um erro assim que terminar de descriptografar a nossa mensagem.

Aqui está o que vamos fazer aqui. O servidor - você pode assumir que é o Apache com SSL aberto - receberá uma mensagem do cliente que considera como texto criptografado ou com algum texto criptografado hipotético criado pelo cliente. A primeira coisa que fazemos com o texto cifrado c é descriptografá-lo usando a fórmula com → (c ^d mod n) = m.

Se você se lembrar da primeira otimização, aplicaremos o teorema do restante chinês e dividiremos o texto em duas partes: uma para calcular pelo mod p, a outra pelo mod q, e depois combinar os resultados. Primeiro, pegue c e represente-o em duas quantidades: a primeira é chamada c ₀ , será igual a mod q, e a segunda é c ₁ , e será igual a c mod p. Então, faremos o mesmo para calcular c para d mod p ec para d mod q.



Em seguida, vamos mudar para a visualização Montgomery, porque isso tornará nossas multiplicações muito rápidas. Então, a próxima coisa que o SSL fará com o seu número é calcular c ₀ ', que será igual a c ₀ R mod q e faça o mesmo aqui abaixo para o valor c1, não anotarei porque parece o mesmo .

Agora que mudamos para a forma de Montgomery, podemos finalmente realizar nossas multiplicações e aqui usaremos a técnica de "janela deslizante". Assim que obtemos c ₀ ', tornamos este simples aumento de c ₀ ' à potência de d no mod q. E aqui, como calculamos esse valor para d, usaremos “janelas deslizantes” para bits do expoente d, e também usaremos o método Karatsuba ou a multiplicação usual, dependendo do tamanho de nossos operandos.



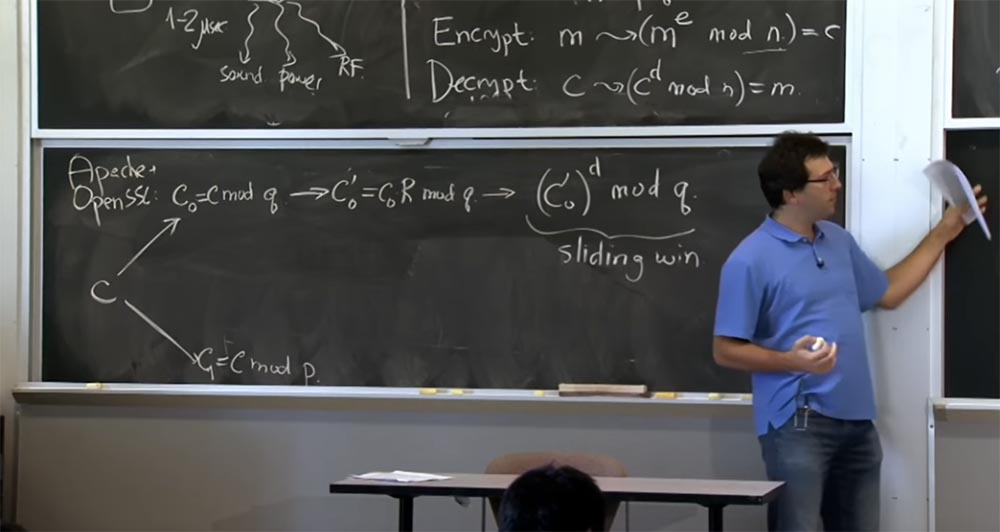
Portanto, se esse valor c ₀ 'e o resultado quadrático obtido anteriormente tiverem o mesmo tamanho, usaremos o método Karatsuba. Se c ₀ 'for muito pequeno, e o resultado anterior da multiplicação for grande, então nós quadrilharemos e multiplicaremos da maneira usual. Aqui usamos "janelas deslizantes" e o método Karatsuba em vez da multiplicação normal.



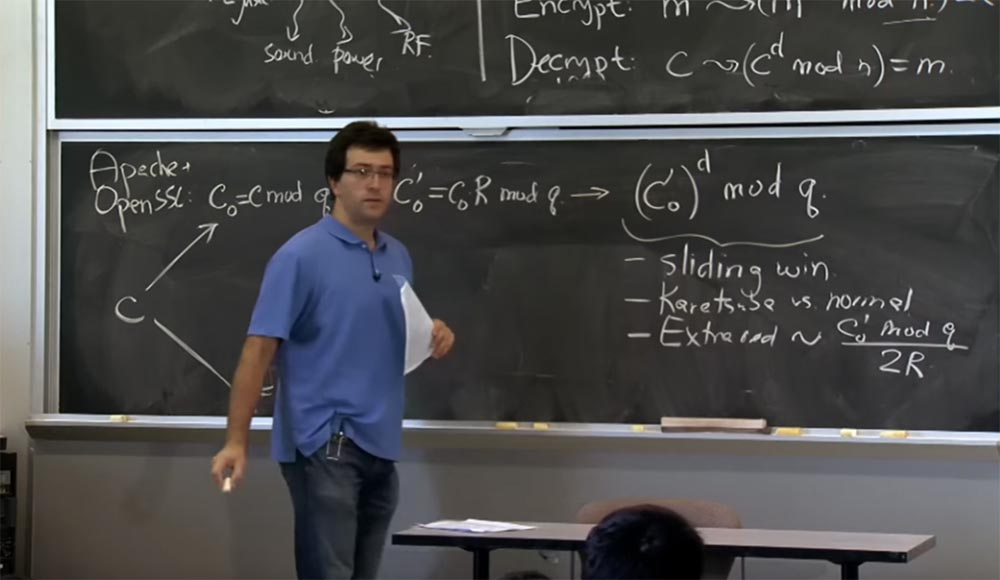
Também nesta fase, reduções adicionais aparecem. Porque a cada multiplicação, reduções adicionais serão proporcionais ao que elevarmos à potência do mod q, ou seja, o valor de (c ₀ ') ^d . Aqui, com uma conexão simples da fórmula, a probabilidade de reduções adicionais será proporcional ao valor c ₀ 'mod q dividido por 2R. É neste local que um pouco aparece que afeta o tempo.

De fato, existem dois efeitos possíveis: usar o método Karatsuba em vez da multiplicação normal e o aparecimento de abreviações adicionais que você fará.

Em um segundo, você verá como ele pode ser usado. Agora, quando você obtiver esse resultado para o mod q e obter um resultado semelhante para o mod p, finalmente poderá recombinar essas duas partes na parte superior e inferior e usar o CRT, o teorema chinês restante.

E o que você obtém do CRT como resultado ... desculpe, acho que precisamos converter isso de volta do formulário Montgomery primeiro. Portanto, antes da recombinação, convertemos a parte superior na expressão (c ₀ ') ^d / R mod q e retornamos nosso valor cd mod q. Na parte inferior, obtemos o cd mod p.

Agora você pode usar o CRT para obter o valor de c ^d mod n. Desculpe pela fonte pequena, eu não tinha quadro-negro suficiente. Sobre a mesma coisa que chegamos aqui abaixo com ₁ , e finalmente podemos obter nosso resultado, ou seja, a mensagem m.



Assim, o servidor pega um pacote recebido, o executa por todo esse pipeline, executa duas partes desse pipeline e termina com uma mensagem descriptografada m igual a cd mod m. Em seguida, ele verificará o preenchimento de preenchimento deste post. No caso de nosso ataque específico, criamos de tal maneira que, de fato, essa adição não corresponde. Escolhemos o valor c para heurísticas que não criptografam a mensagem real com a adição correta de preenchimento.

Portanto, o complemento não passa no teste, o servidor precisará registrar um erro, enviar uma mensagem de erro ao cliente e desconectar. Portanto, mediremos o tempo que o servidor levará para passar nossa mensagem por esse pipeline. Você tem perguntas sobre o processo de processar uma mensagem pelo servidor e combinar todas essas otimizações?

Público: na minha opinião, há um erro com um índice de magnitude c.

Professor: sim, você está certo, estou adicionando o índice 0, aqui deve estar c ₀ ^d mod q.



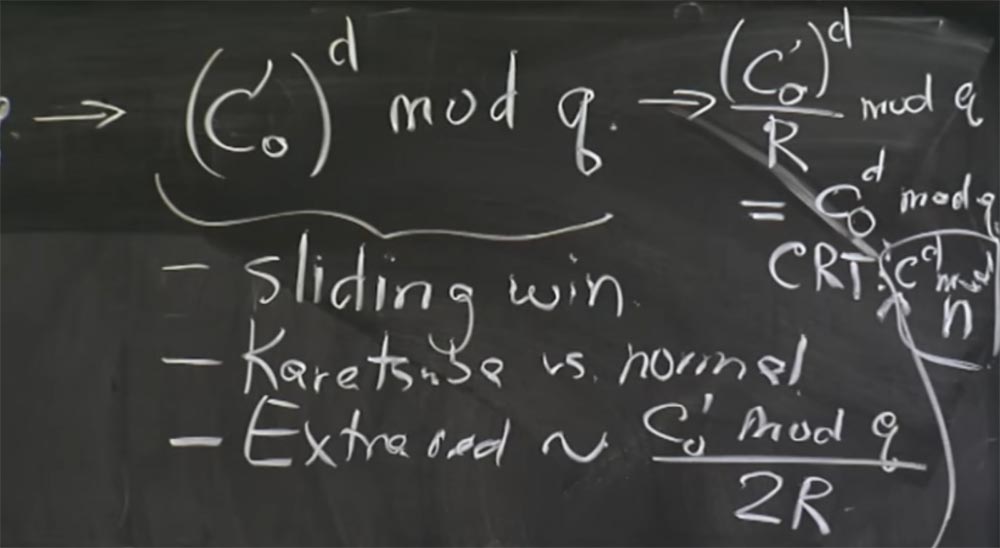Público: quando você divide por R mod q, não há suposições sobre quanto q você deve adicionar para reduzir ainda mais os bits baixos em zeros?

Professor: sim, você está certo, nesta fase final (c ₀ ') ^d / R mod q pode haver reduções adicionais. Portanto, devemos fazer essa divisão por R da maneira correta, e provavelmente devemos fazer a mesma coisa que fazer a redução de Montgomery aqui, quando dividimos por R, para converter o valor de volta. Como no início dos cálculos não está claro exatamente quanto q devemos adicionar, usamos o método de seleção, destruímos os zeros baixos e, novamente, fazemos o mod q e, possivelmente, uma redução adicional. Você está absolutamente correto, neste caso, é exatamente a mesma divisão por R mod q que para cada etapa da multiplicação de Montgomery.

Então, como você tira proveito disso? Como um invasor pode resolver a chave secreta de um servidor medindo o tempo necessário para concluir as operações? Esses caras têm um plano baseado em adivinhar um bit de chave privada por vez. Podemos assumir que a chave secreta é o expoente criptografado d, porque você sabe e e sabe n, essa é a chave pública. A única coisa que você não sabe é d.



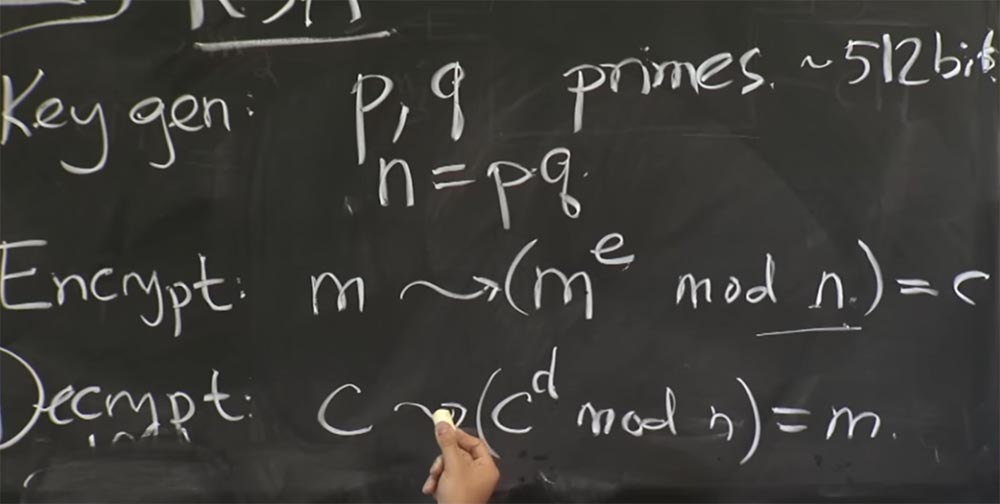
De fato, nesse ataque, eles não adivinham diretamente o valor de d, pois é bastante complicado. Em vez disso, eles consideram q ou p, independentemente de qual dessas duas quantidades. Depois de adivinhar o que p ou q importa, você pode calcular n = pq. Então, se você conhece os valores de p e q, pode calcular a função φ sobre a qual falamos anteriormente. Isso permitirá que você obtenha o valor de d a partir do valor de e. Portanto, essa fatoração do valor de n é extremamente importante; deve ser mantida em segredo para garantir a segurança da RSA.

Na verdade, esses caras pretendiam adivinhar o valor q analisando os tempos desse pipeline. O que eles estão fazendo para isso? Eles selecionam cuidadosamente o valor inicial do valor de c e medem o tempo de sua passagem pelo pipeline do servidor.

Em particular, há duas partes nesse ataque e você deve executar algumas etapas iniciais para adivinhar os primeiros bits. Então, assim que você tiver os primeiros bits, poderá adivinhar o próximo. Portanto, não permita que eu diga detalhadamente como eles adivinham o primeiro par de bits, porque na verdade é muito mais interessante considerar como eles adivinham o próximo bit. Se tivermos tempo, voltaremos a como a adivinhação de vários bits iniciais é descrita em um artigo de aula.

Então, suponha que você tenha suposição g sobre quais bits estão no valor desse q. Deixe esse valor consistir em tais bits: g = g ₀ g ₁ g ₂ ... e assim por diante. Em vez disso, nem sequer é g, mas os bits reais de q, então deixe-me reescrevê-lo assim: g = q ₀ q ₁ q ₂ .... Acreditamos que esses q são bits altos, e estamos tentando adivinhar os bits cada vez mais baixos. Suponha que sabemos o valor de q até o bit qj e, em seguida, todos os zeros seguem. Você não tem idéia do que são os outros bits.



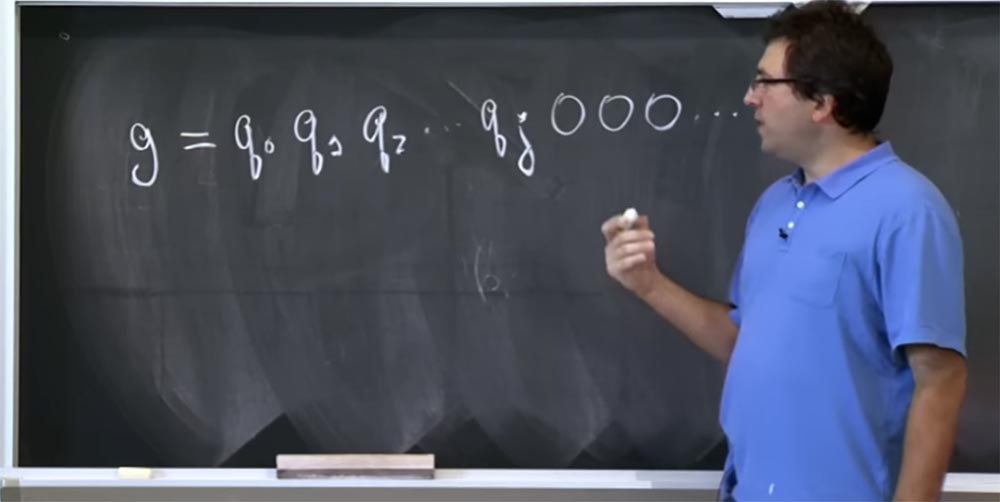
Esses caras tentaram injetar essa conjectura g neste local do nosso pipeline: (c0 ') d mod q. Como esse é o local em que dois tipos de otimização são usados: o método Karatsub, em vez da multiplicação usual e um número diferente de abreviações adicionais, dependendo do valor de c ₀ '. Na verdade, eles tentaram introduzir duas suposições diferentes nesse local do pipeline: o primeiro, que se parece com g = q ₀ q ₁ q ₂ ... qj 000 ... 0000, e o segundo, que eles chamaram de g _high , que consiste nos mesmos bits altos, mas em vez disso de todos os zeros no final, há uma unidade que indica um bit alto, seguida por zeros novamente:

g = q ₀ q ₁ q ₂ ... qj 100 ... 0000.

Como isso ajuda esses caras a entender o que está acontecendo? Existem duas maneiras de fazer isso. Suponha que nosso palpite g seja igual ao valor c ₀ '. Podemos assumir que esses g e g _altos correspondem ao valor c ₀ 'dado na placa esquerda. Na verdade, é bem simples fazer isso porque c ₀ 'é muito fácil de calcular a partir do valor de entrada criptografado c ₀ , basta multiplicá-lo por R.



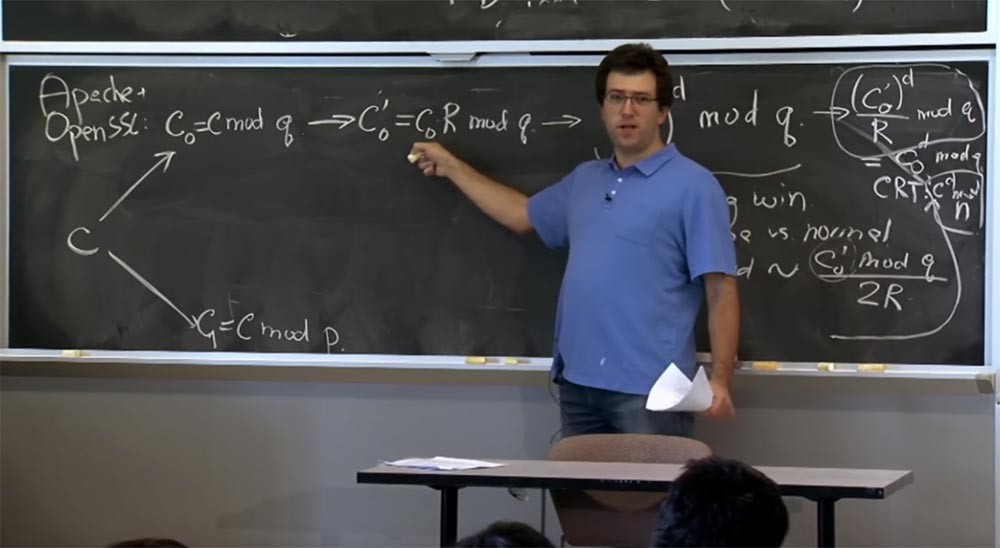
Portanto, para adivinhar o valor (c ₀ ') ^d , eles apenas precisam adivinhar, adivinhar g e primeiro dividi-lo por R, ou seja, dividir por 512 mod algo lá. Em seguida, eles o apresentarão novamente, o servidor o multiplicará por R e continuará o processo descrito em nosso esquema de pipeline.

Então, suponha que possamos colocar nosso valor inteiro selecionado específico no lugar certo. Então, qual será o tempo de computação c ₀ 'para d mod q?



Existem duas opções possíveis em que q se encaixa nessa imagem. Pode ser que q esteja entre esses dois valores de g e g _altos , porque o próximo bit de q é 0. Portanto, esse valor - o primeiro 0 após qj - será menor que q, mas esse valor - 1 após q - será maior que q Isso acontece se o próximo bit de q for 0, ou é possível que q esteja acima desses dois valores se o próximo bit de q for 1.



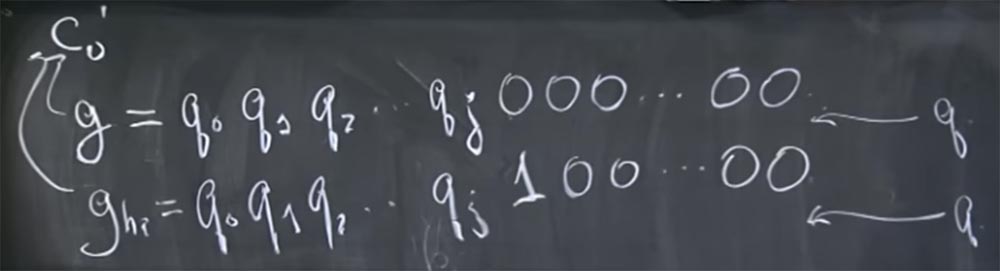
Agora, podemos dizer qual será o tempo de descriptografia desses dois valores se q estiver entre eles ou se q estiver localizado acima de ambos.

Vejamos a situação em que q está localizado acima. Nesse caso, tudo é praticamente o mesmo. Como esses dois valores são menores que q, o valor dessas coisas no mod q será aproximadamente o mesmo. Eles são um pouco diferentes devido a esse bit extra, mas ainda mais ou menos do mesmo tamanho. E o número de reduções adicionais, redução extra, provavelmente também não diferirá muito, porque é proporcional ao valor de c0 'mod q. E para os valores _{altos de} g e g menores que q, eles são todos iguais. Nenhum deles excederá q e não causará um grande número de reduções adicionais, porque para q maior que essas duas suposições, o número de cálculos pelo método Karatsuba com relação ao número de cálculos comuns permanecerá o mesmo. Em termos desse relacionamento, o servidor manipulará tanto g quanto g _alto igualmente. Portanto, o servidor está prestes a criar a mesma quantidade de abreviações adicionais para esses dois valores. Portanto, se você perceber que o servidor está gastando o mesmo tempo respondendo a essas suposições, provavelmente deve assumir que existe realmente 1 no valor de g _alto neste momento.



Por outro lado, se q estiver localizado entre esses dois valores, existem duas coisas possíveis que podem causar alterações de comutação e tempo. Uma das coisas é que, como g _{alta é} um pouco maior que q, o número de cortes adicionais será proporcional a c ₀ 'mod q, que é muito pequeno porque c ₀ ' é q mais alguns bits nessa sequência de bits extra de 100 ... 00 Assim, o número de reduções adicionais será mais perceptível e tudo começará a acontecer mais rapidamente.
, , , , , : «, !». , g c ₀ ' , q, , g _high q, g _high mod q . , . – , , .

c ₀ ' mod q. c ₀ g _high , q, , g q. , . , , . , 32- , .

, 32- , , , . , . 32 , , - . , , 32, , , , .

, , , . , q 1, , q 0, , g _high q , , .

. , . , . , , 1-2 . , , Ethernet.
, . . , 7 . , , -, , ?

: ?

: , , , , , . , .

, , 7 , , 7 . 7 g, 7 g + 1, g + 2 7 g + 400. g, g, , 7 400, ?



: , , ?

: , , , — (c ₀ ') ^d . . , , , mod p. , , . , g, 1, 2, 3, , .

, , – 100…00. , mod p, , mod p . « », , (c ₀ ') ^d , . ?

: , ?

: - , q. , q, , , .

: c ₀ '?

: c ₀ ', c, c ₀ ' R mod n.



, «» , c ₀ = mod q, c ₀ = ((c ₀ ' R ^-1 ) mod n) mod q. R, R. c ₀ ', (c ₀ ') ^d mod q. , , , , R. , R = 2 ⁵¹² . , .

: mod p ?

:ou seja, você não sabe o que é p, mas deseja defini-lo aleatoriamente? Se você tiver sucesso, fará um ótimo trabalho! Bem, na próxima semana começaremos a discutir outras questões.


A versão completa do curso está disponível aqui .

Obrigado por ficar conosco. Você gosta dos nossos artigos? Deseja ver materiais mais interessantes? Ajude-nos fazendo um pedido ou recomendando a seus amigos, um desconto de 30% para os usuários da Habr em um análogo exclusivo de servidores básicos que inventamos para você: Toda a verdade sobre o VPS (KVM) E5-2650 v4 (6 núcleos) 10GB DDR4 240GB SSD 1Gbps de US $ 20 ou como dividir o servidor? (as opções estão disponíveis com RAID1 e RAID10, até 24 núcleos e até 40GB DDR4).

VPS (KVM) E5-2650 v4 (6 núcleos) 10 GB DDR4 240 GB SSD de 1 Gbps até dezembro de graça quando pagar por um período de seis meses, você pode fazer o pedido aqui .

Dell R730xd 2 vezes mais barato? Somente nós temos 2 TVs Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 a partir de US $ 249 na Holanda e nos EUA! Leia sobre Como criar um prédio de infraestrutura. classe usando servidores Dell R730xd E5-2650 v4 custando 9.000 euros por um centavo?