🌶️ 🐴 🕴🏻 Julia e o movimento de uma partícula carregada em um campo eletromagnético 👨‍🏭 ✍🏻 🎯

Fortalecemos as habilidades de resolução e visualização de equações diferenciais usando uma das equações evolutivas mais comuns como exemplo, lembre-se do bom e velho Scilab e tente entender se precisarmos ... Sob a imagem cortada (kilobytes por setecentos)

Verifique se o software está atualizado

julia>] (v1.0) pkg>update #   (v1.0) pkg> status Status `C:\Users\\.julia\environments\v1.0\Project.toml` [537997a7] AbstractPlotting v0.9.0 [ad839575] Blink v0.8.1 [159f3aea] Cairo v0.5.6 [5ae59095] Colors v0.9.5 [8f4d0f93] Conda v1.1.1 [0c46a032] DifferentialEquations v5.3.1 [a1bb12fb] Electron v0.3.0 [5789e2e9] FileIO v1.0.2 [5752ebe1] GMT v0.5.0 [28b8d3ca] GR v0.35.0 [c91e804a] Gadfly v1.0.0+ #master (https://github.com/GiovineItalia/Gadfly.jl.git) [4c0ca9eb] Gtk v0.16.4 [a1b4810d] Hexagons v0.2.0 [7073ff75] IJulia v1.14.1+ [`C:\Users\\.julia\dev\IJulia`] [6218d12a] ImageMagick v0.7.1 [c601a237] Interact v0.9.0 [b964fa9f] LaTeXStrings v1.0.3 [ee78f7c6] Makie v0.9.0+ #master (https://github.com/JuliaPlots/Makie.jl.git) [7269a6da] MeshIO v0.3.1 [47be7bcc] ORCA v0.2.0 [58dd65bb] Plotly v0.2.0 [f0f68f2c] PlotlyJS v0.12.0+ #master (https://github.com/sglyon/PlotlyJS.jl.git) [91a5bcdd] Plots v0.21.0 [438e738f] PyCall v1.18.5 [d330b81b] PyPlot v2.6.3 [c4c386cf] Rsvg v0.2.2 [60ddc479] StatPlots v0.8.1 [b8865327] UnicodePlots v0.3.1 [0f1e0344] WebIO v0.4.2 [c2297ded] ZMQ v1.0.0

Vamos ver os guias anteriores

e prossiga para a declaração do problema

O movimento de partículas carregadas em um campo eletromagnético

Em uma partícula carregada com uma carga $q$ movendo-se em EMF com velocidade $u$ a força de Lorentz age: $\ vec {F} _L = q \ left (\ vec {E} + \ left [\ vec {u} \ times \ vec {B} \ right] \ right)$ . Esta fórmula é válida com várias simplificações. Negligenciando correções à teoria da relatividade, consideramos a massa de partículas constante, de modo que a equação do movimento tem a forma: $\ frac {d} {dt} (m \ vec {u}) = q \ left (\ vec {E} + \ left [\ vec {u} \ times \ vec {B} \ right] \ right] \ direita)$

Vamos direcionar o eixo Y ao longo do campo elétrico, o eixo Z ao longo do campo magnético e assumir por simplicidade que a velocidade inicial da partícula se encontra no plano XY. Nesse caso, toda a trajetória da partícula também estará neste plano. As equações de movimento terão a forma:

\ left \ {\ begin {matrix} m \ ddot {x} = qB \ ponto {y} \\ m \ ddot {y} = qE-qB \ ponto {x} \ end {matriz} \ right.

$\ left \ {\ begin {matrix} m \ ddot {x} = qB \ ponto {y} \\ m \ ddot {y} = qE-qB \ ponto {x} \ end {matriz} \ right.$

Incomensurável: $x ^ * = \ frac {x} {\ lambda}, \, y ^ * = \ frac {y} {\ lambda}, \, \ tau = \ frac {ct} {\ lambda}, \, B ^ * = \ frac {Bmc} {q \ lambda}, \, E ^ * = \ frac {Emc ^ 2} {q \ lambda}$ . Asteriscos indicam quantidades dimensionais e $\ lambda$ - o tamanho característico do sistema físico considerado. Obtemos um sistema adimensional de equações de movimento de uma partícula carregada em um campo magnético:

\ left \ {\ begin {matrix} \ frac {d ^ 2x} {d \ tau ^ 2} = B \ frac {dy} {d \ tau} \\ \ frac {d ^ 2y} {d \ tau ^ 2} = EB \ frac {dx} {d \ tau} \ end {matriz} \ right.

$\ left \ {\ begin {matrix} \ frac {d ^ 2x} {d \ tau ^ 2} = B \ frac {dy} {d \ tau} \\ \ frac {d ^ 2y} {d \ tau ^ 2} = EB \ frac {dx} {d \ tau} \ end {matriz} \ right.$

Vamos abaixar a ordem:

\ left \ {\ begin {matrix} \ frac {dx} {d \ tau} = U_x \\ \ frac {dy} {d \ tau} = U_y \\ \ frac {dU_x} {d \ tau} = BU_y \\ \ frac {dU_y} {d \ tau} = E-BU_x \ end {matriz} \ right.

$\ left \ {\ begin {matrix} \ frac {dx} {d \ tau} = U_x \\ \ frac {dy} {d \ tau} = U_y \\ \ frac {dU_x} {d \ tau} = BU_y \\ \ frac {dU_y} {d \ tau} = E-BU_x \ end {matriz} \ right.$

Como configuração inicial do modelo, escolhemos: $B = 2$ T $E = 5 \ cdot 10 ^ 4$ V / m $v_0 = 7 \ cdot 10 ^ 4$ m / s Para uma solução numérica, usamos o pacote DifferentialEquations :

Código e Gráficos

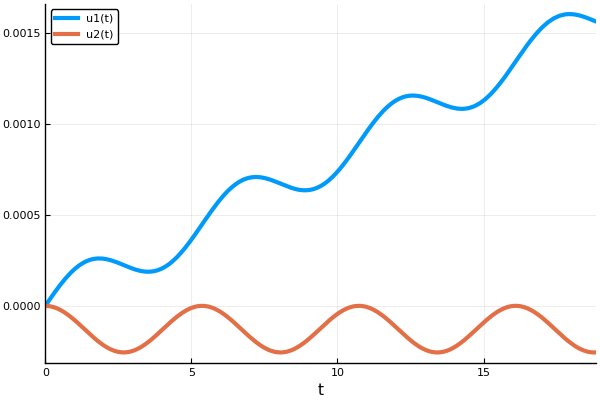
 using DifferentialEquations, Plots pyplot() M = 9.11e-31 # kg q = 1.6e-19 # C C = 3e8 # m/s λ = 1e-3 # m function modelsolver(Bo = 2., Eo = 5e4, vel = 7e4) B = Bo*q*λ / (M*C) E = Eo*q*λ / (M*C*C) vel /= C A = [0. 0. 1. 0.; 0. 0. 0. 1.; 0. 0. 0. B; 0. 0. -B 0.] syst(u,p,t) = A * u + [0.; 0.; 0.; E] # ODE system u0 = [0.0; 0.0; vel; 0.0] # start cond-ns tspan = (0.0, 6pi) # time period prob = ODEProblem(syst, u0, tspan) # problem to solve sol = solve(prob, Euler(), dt = 1e-4, save_idxs = [1, 2], timeseries_steps = 1000) end Solut = modelsolver() plot(Solut)

Aqui usamos o método Euler, para o qual o número de etapas é especificado. Além disso, nem toda a solução do sistema é salva na matriz de respostas, mas apenas 1 e 2 índices, ou seja, as coordenadas do X e do player (não precisamos de velocidades).

 X = [Solut.u[i][1] for i in eachindex(Solut.u)] Y = [Solut.u[i][2] for i in eachindex(Solut.u)] plot(X, Y, xaxis=("X"), background_color=RGB(0.1, 0.1, 0.1)) title!(" ") yaxis!("Y") savefig("XY1.png")#

Verifique o resultado. Introduzimos uma nova variável em vez de x $\ til {x} = x-ut$ . Assim, é feita uma transição para um novo sistema de coordenadas que se move em relação ao original com uma velocidade u na direção do eixo X :

\ left \ {\ begin {matrix} \ ddot {\ til {x}} = qB \ ponto {y} / m \\ \ ddot {y} = qE / m-qB \ ponto {x} / m -qBu / m \ end {matriz} \ direita.

$\ left \ {\ begin {matrix} \ ddot {\ til {x}} = qB \ ponto {y} / m \\ \ ddot {y} = qE / m-qB \ ponto {x} / m -qBu / m \ end {matriz} \ direita.$

Se você escolher $u = E / B$ e denotar $\ omega = qB / m$ , o sistema será simplificado:

\ left \ {\ begin {matrix} \ ddot {\ til {x}} = \ omega \ dot {y} \\ \ ddot {y} = - \ omega \ dot {\ tilde {x}} \ end { matriz} \ direita.

$\ left \ {\ begin {matrix} \ ddot {\ til {x}} = \ omega \ dot {y} \\ \ ddot {y} = - \ omega \ dot {\ tilde {x}} \ end { matriz} \ direita.$

O campo elétrico desapareceu das últimas igualdades e são as equações de movimento de uma partícula sob a influência de um campo magnético uniforme. Assim, a partícula no novo sistema de coordenadas (x, y) deve se mover em um círculo. Como esse novo sistema de coordenadas se move em relação ao original com velocidade $u = E / B$ , o movimento resultante das partículas consistirá em um movimento uniforme ao longo do eixo X e rotação ao redor do círculo no plano XY . Como você sabe, a trajetória que ocorre quando esses dois movimentos são somados geralmente é um trocóide . Em particular, se a velocidade inicial é zero, o caso mais simples de movimento desse tipo é realizado - ao longo do ciclóide .
Vamos garantir que a velocidade da deriva seja realmente igual a E / V. Para fazer isso:

estragaremos a matriz de resposta definindo um valor deliberadamente mais baixo em vez do primeiro elemento (máximo)
encontramos o número do elemento máximo na segunda coluna da matriz de resposta, que é atrasada pelas ordenadas
calculamos a velocidade de desvio sem dimensão dividindo o valor máximo de abscissa pelo valor de tempo correspondente

 Y[1] = -0.1 numax = argmax( Y ) X[numax] / Solut.t[numax]

Saída: 8.334546850446588e-5

 B = 2*q*λ / (M*C) E = 5e4*q*λ / (M*C*C) E/B

Saída: 8.33333333333333332e-5
Até sétima ordem!
Por conveniência, definimos uma função que aceita os parâmetros do modelo e a assinatura do gráfico, que também servirá como o nome do arquivo png criado na pasta do projeto (funciona em Juno / Atom e Jupyter). Diferentemente do Gadfly , onde os gráficos foram criados em camadas e exibidos pela função plot () , em Plots, para criar gráficos diferentes em um quadro, o primeiro deles é criado pela função plot () e os subseqüentes são adicionados usando plot! () . Os nomes de funções que alteram os objetos aceitos em Julia costumam terminar com um ponto de exclamação.

 function plotter(ttle = "qwerty", Bo = 2, Eo = 4e4, vel = 7e4) Ans = modelsolver(Bo, Eo, vel) X = [Ans.u[i][1] for i in eachindex(Ans.u)] Y = [Ans.u[i][2] for i in eachindex(Ans.u)] plot!(X, Y) p = title!(ttle) savefig( p, ttle * ".png" ) end

À velocidade inicial zero, como esperado, obtemos um ciclóide :

 plot() plotter("Zero start velocity", 2, 4e4, 7e4)

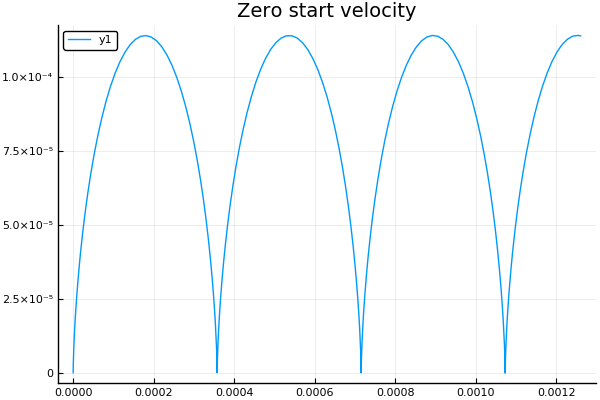
Obtemos a trajetória da partícula quando a indução, intensidade e quando o sinal de carga muda. Deixe-me lembrá-lo de que um ponto significa a execução seqüencial de uma função com todos os elementos da matriz

Escondido

 plot() plotter.("B   ", 0, [3e4 4e4 5e4 6e4] )

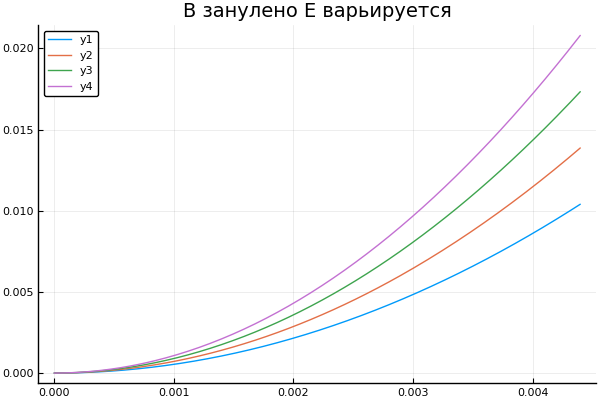
 plot() plotter.("E  B ", [1 2 3 4], 0 )

 q = -1.6e-19 # C plot() plotter.(" ")

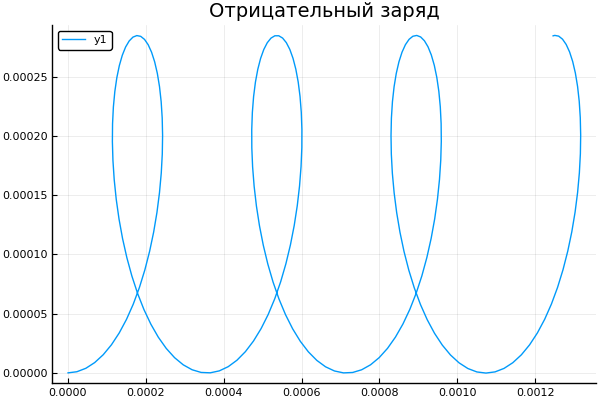
E vamos ver como a mudança na velocidade inicial afeta a trajetória da partícula:

 plot() plotter.(" ", 2, 5e4, [2e4 4e4 6e4 8e4] )

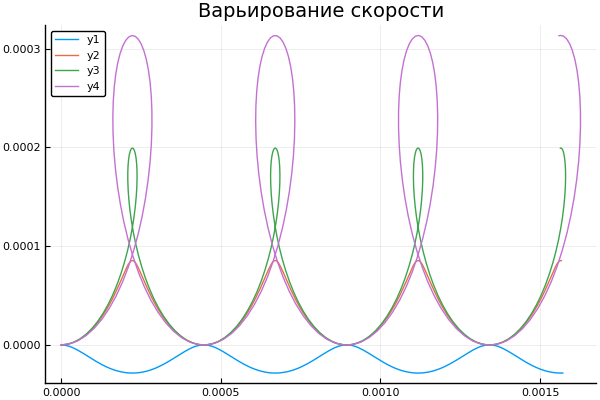
Um pouco sobre o Scilab

Em Habré já há informações suficientes sobre Silab, por exemplo 1 , 2 , e aqui sobre a Octave, portanto, nos limitaremos a links para a Wikipedia e para a página inicial .

Por conta própria, adicionarei sobre a presença de uma interface conveniente com caixas de seleção, botões e gráficos e uma ferramenta de modelagem visual Xcos bastante interessante. O último pode ser usado, por exemplo, para simular um sinal na engenharia elétrica:

Spoiler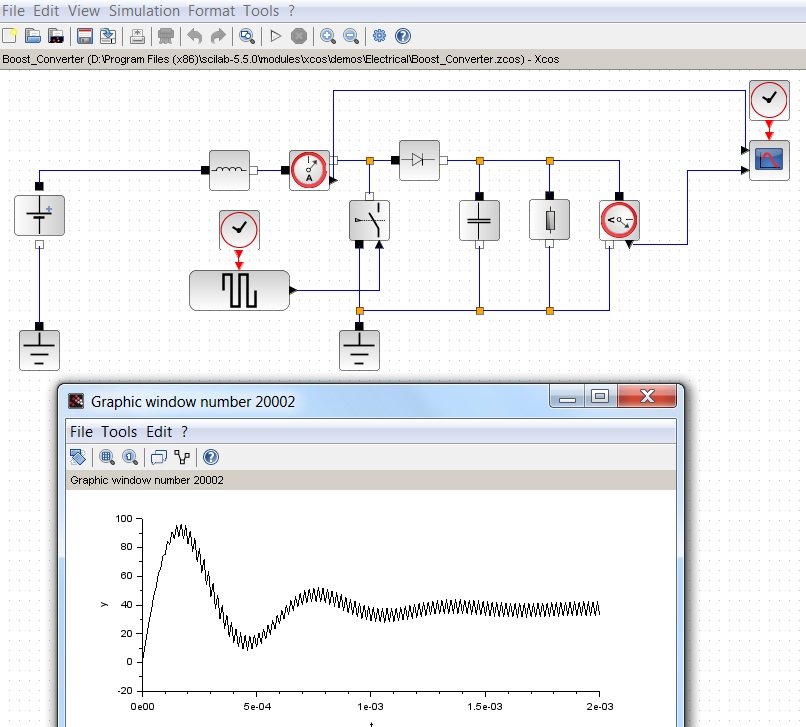

E aqui está um guia muito conveniente:

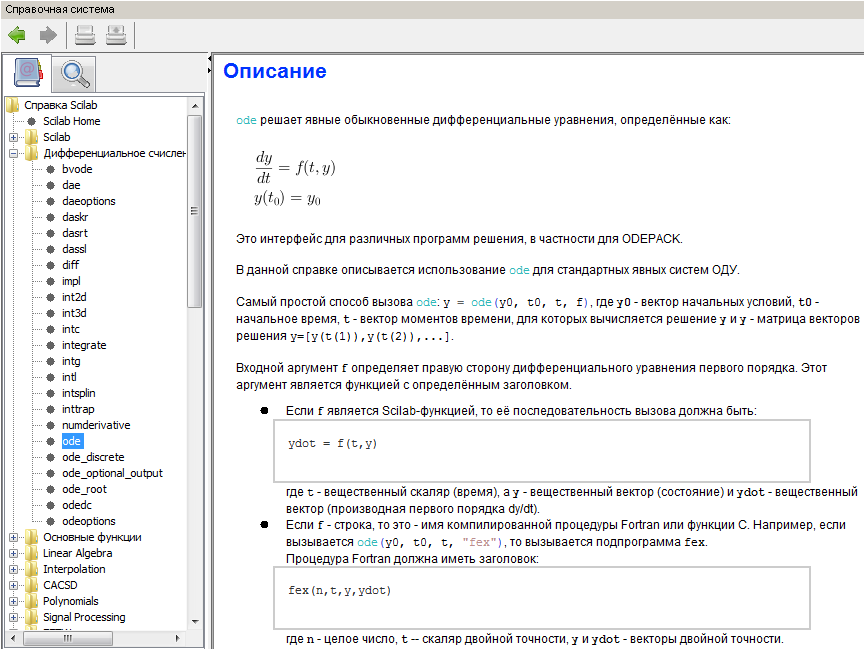
Na verdade, nossa tarefa também pode ser resolvida no Scilab:

Código e imagens

 clear function du = syst(t, u, A, E) du = A * u + [0; 0; 0; E] // ODE system endfunction function [tspan, U] = modelsolver(Bo, Eo, vel) B = Bo*q*lambda / (M*C) E = Eo*q*lambda / (M*C*C) vel = vel / C u0 = [0; 0; vel; 0] // start cond-ns t0 = 0.0 tspan = t0:0.1:6*%pi // time period A = [0 0 1 0; 0 0 0 1; 0 0 0 B; 0 0 -B 0] U = ode("rk", u0, t0, tspan, list(syst, A, E) ) endfunction M = 9.11e-31 // kg q = 1.6e-19 // C C = 3e8 // m/s lambda = 1e-3 // m [cron, Ans1] = modelsolver( 2, 5e4, 7e4 ) plot(cron, Ans1 ) xtitle ("   ","t","x, y, dx/dt, dy/dt"); legend ("x", "y", "Ux", "Uy"); scf(1)//    plot(Ans1(1, :), Ans1(2, :) ) xtitle (" ","x","y"); xs2png(0,'graf1');//       xs2jpg(1,'graf2');// ,  -

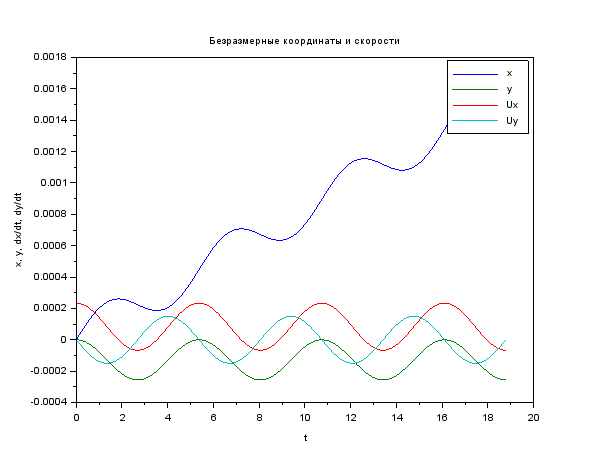
A seguir, há informações sobre a função de solução de ode. Em princípio, a pergunta implora

Por que precisamos da Julia?

... se existem coisas maravilhosas como Scilab, Octave e Numpy, Scipy?
Sobre os dois últimos, não direi - ainda não tentei. E, em geral, a questão é complicada, então vamos dar uma olhada rápida:

Scilab
Em um disco rígido, são necessários pouco mais de 500 MB, é iniciado rapidamente e imediatamente há cálculos diferenciais disponíveis, gráficos e tudo mais. Bom para iniciantes: um excelente guia (principalmente localizado), existem muitos livros em russo. Sobre erros internos já foi dito aqui e aqui , e como o produto é muito nicho, a comunidade é lenta e os módulos adicionais são muito escassos.

Julia
À medida que os pacotes são adicionados (especialmente qualquer python-a la Jupyter e Mathplotlib), ele cresce de 376 MB para pouco mais de seis gigabytes. Ela também não poupa RAM: no início de 132 MB e depois de planejar os planejamentos em Júpiter, ele alcançará calmamente 1 GB. Se você trabalha no Juno , tudo é quase como no Scilab : você pode executar o código imediatamente no intérprete, imprimir no bloco de notas incorporado e salvá-lo como um arquivo, existe um navegador variável, um log de comandos e ajuda on-line. Pessoalmente, estou indignado com a falta de clear () , ou seja, executei o código, comecei a corrigi-lo e renomeá-lo, e as variáveis antigas permaneceram (não há navegador de variáveis em Júpiter).

Mas tudo isso não é crítico. O Scilab é bastante adequado para o primeiro casal, fazer uma testa, um cursor ou calcular algo entre eles é uma ferramenta muito improvisada. Embora também haja suporte para computação paralela e chamada de funções sishn / Fortran, para as quais não pode ser usado com seriedade. Matrizes grandes o aterrorizam; para definir as multidimensionais, você precisa lidar com todos os tipos de obscurantismo , e cálculos além do escopo das tarefas clássicas podem deixar tudo junto com o sistema operacional.

E depois de todas essas dores e decepções, você pode mudar com segurança para Julia para procurar aqui também. Continuaremos a estudar, o benefício da comunidade é muito receptivo, os problemas se resolvem rapidamente e Julia tem muitos recursos mais interessantes que transformarão o processo de aprendizado em uma jornada emocionante!

Julia e o movimento de uma partícula carregada em um campo eletromagnético

O movimento de partículas carregadas em um campo eletromagnético

Um pouco sobre o Scilab

Por que precisamos da Julia?

More articles: