Então, outro artigo do ciclo da
"matemática nos dedos ". Hoje
continuamos a discussão sobre métodos de mínimos quadrados, mas desta vez do ponto de vista do programador. Este é outro artigo da série, mas destaca-se, pois geralmente não requer nenhum conhecimento de matemática. O artigo foi concebido como uma introdução à teoria; portanto, a partir de habilidades básicas, é necessário ativar o computador e escrever cinco linhas de código. Obviamente, não vou me debruçar sobre este artigo e, em um futuro próximo, publicarei uma sequência. Se eu encontrar tempo suficiente, escreverei um livro deste material. O público-alvo são programadores, então Habr é o lugar certo para invadir. Em geral, eu não gosto de escrever fórmulas e gosto muito de aprender com os exemplos, parece-me que é muito importante - não apenas olhar para os rabiscos no conselho escolar, mas para tentar de tudo.
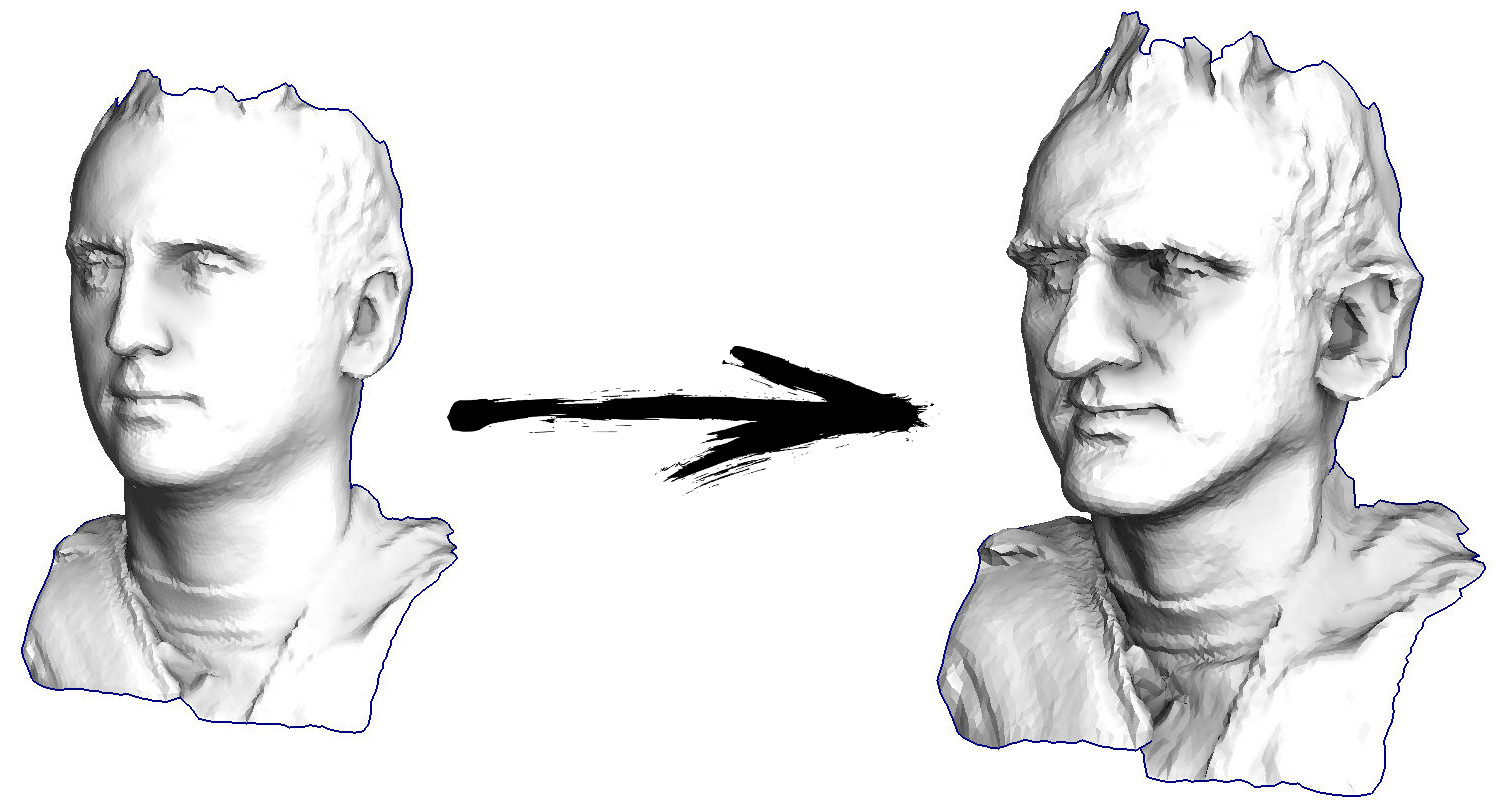
Então, vamos começar. Vamos imaginar que eu tenho uma superfície triangular com uma digitalização do meu rosto (na figura à esquerda). O que preciso fazer para aprimorar os recursos, transformando essa superfície em uma máscara grotesca?
Nesse caso em particular, resolvo uma equação diferencial elíptica chamada
Simeon Demi Poisson . Caros programadores, vamos jogar um jogo: adivinhe quantas linhas existem no código C ++ que decidem isso? Bibliotecas de terceiros não podem ser chamadas, apenas temos um compilador à nossa disposição. A resposta está sob o corte.
De fato, vinte linhas de código são suficientes para um solucionador. Se você contar com tudo, tudo, inclusive o analisador do arquivo de modelo 3D, mantenha-o dentro de duzentas linhas - apenas cuspa.
Exemplo 1: suavização de dados
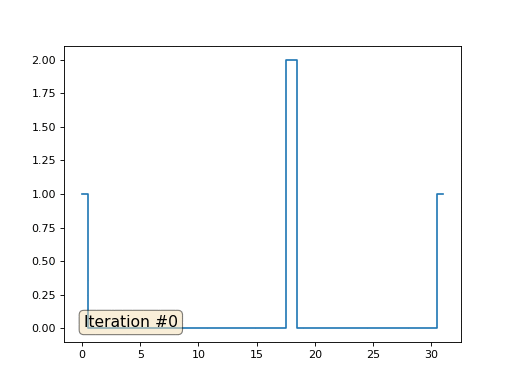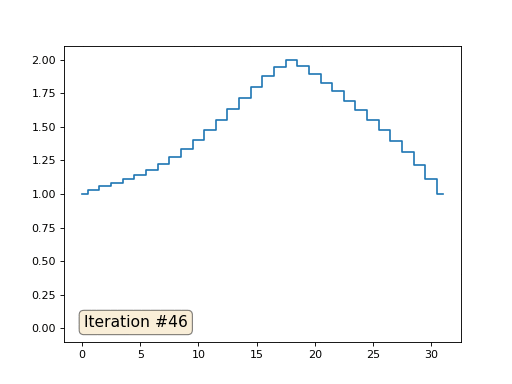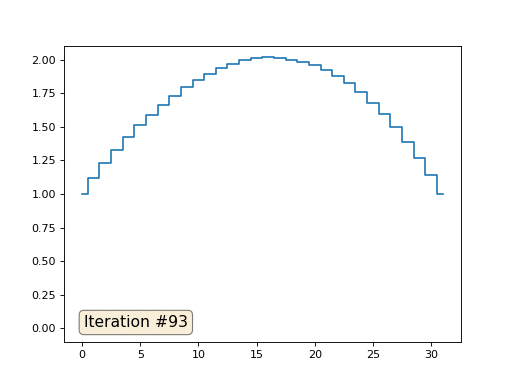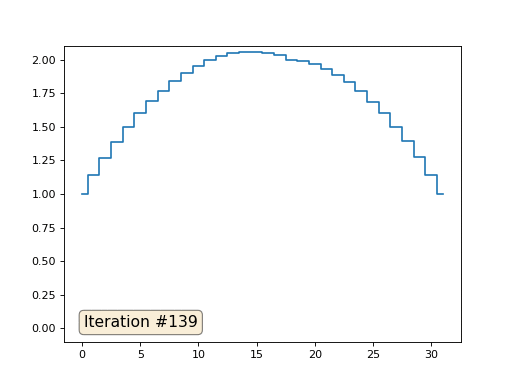
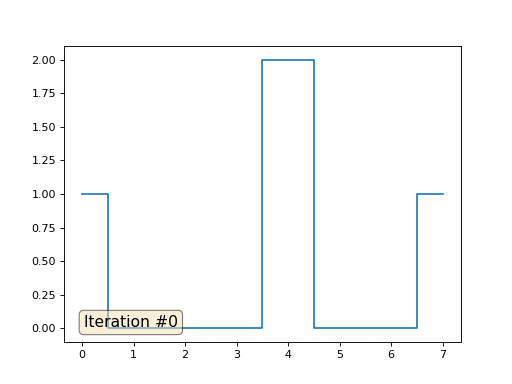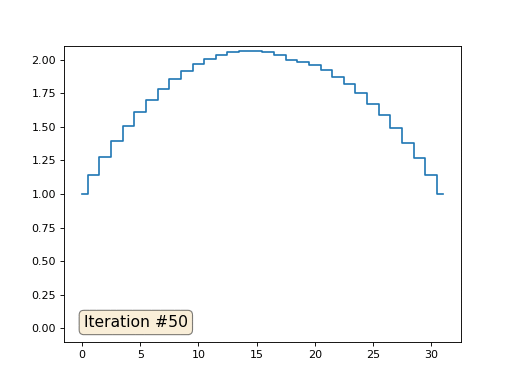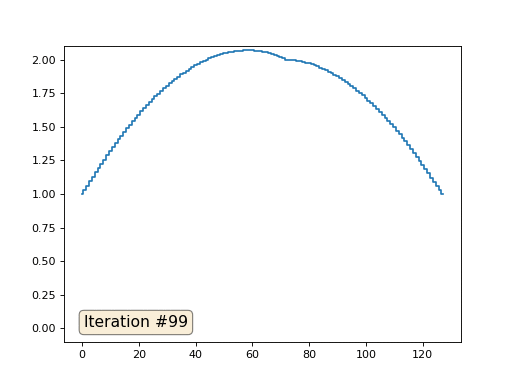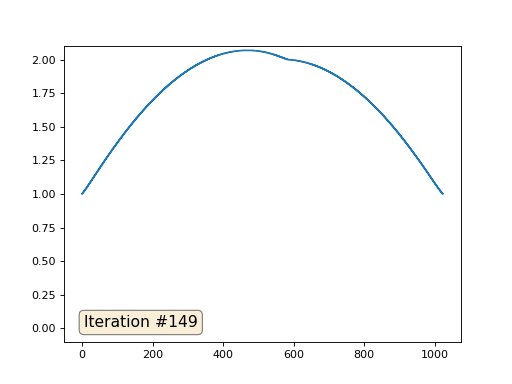
Vamos falar sobre como isso funciona. Vamos começar de longe, imagine que temos uma matriz regular f, por exemplo, de 32 elementos, inicializada da seguinte maneira:

E então executaremos o seguinte procedimento mil vezes: para cada célula f [i], escrevemos nela o valor médio das células vizinhas: f [i] = (f [i-1] + f [i + 1]) / 2. Para deixar mais claro, aqui está o código completo:
import matplotlib.pyplot as plt f = [0.] * 32 f[0] = f[-1] = 1. f[18] = 2. plt.plot(f, drawstyle='steps-mid') for iter in range(1000): f[0] = f[1] for i in range(1, len(f)-1): f[i] = (f[i-1]+f[i+1])/2. f[-1] = f[-2] plt.plot(f, drawstyle='steps-mid') plt.show()
Cada iteração suaviza os dados de nossa matriz e, após mil iterações, obteremos um valor constante em todas as células. Aqui está uma animação das primeiras cento e cinquenta iterações:
Se não estiver claro para você por que o anti-aliasing ocorre, pare agora mesmo, pegue uma caneta e tente desenhar exemplos; caso contrário, não faz sentido ler mais. A superfície triangulada é essencialmente a mesma que neste exemplo. Imagine que, para cada vértice, encontremos seus vizinhos, calculemos seu centro de massa e movemos nosso vértice para esse centro de massa, e assim por dez vezes. O resultado será assim:

Obviamente, se você não parar em dez iterações, depois de um tempo toda a superfície será compactada para um ponto exatamente da mesma maneira que no exemplo anterior, toda a matriz ficará preenchida com o mesmo valor.
Exemplo 2: aprimorando / atenuando recursos
O código completo
está disponível no github , mas aqui darei a parte mais importante, omitindo apenas a leitura e gravação de modelos 3D. Portanto, o modelo triangulado para mim é representado por duas matrizes: verts e faces. A matriz verts é apenas um conjunto de pontos tridimensionais, são os vértices da malha poligonal. A matriz de faces é um conjunto de triângulos (o número de triângulos é igual a faces.size ()), para cada triângulo, os índices da matriz de vértices são armazenados na matriz. O formato dos dados e o trabalho com ele descrevi em detalhes no
meu curso de palestras sobre computação gráfica. Há também uma terceira matriz, que recordo das duas primeiras (mais precisamente, apenas da matriz de faces) - vvadj. Essa é uma matriz que para cada vértice (o primeiro índice de uma matriz bidimensional) armazena os índices de seus vizinhos (segundo índice).
std::vector<Vec3f> verts; std::vector<std::vector<int> > faces; std::vector<std::vector<int> > vvadj;
A primeira coisa que faço é que, para cada vértice da minha superfície, considero o vetor de curvatura. Vamos ilustrar: para o vértice atual v, eu itero sobre todos os seus vizinhos n1-n4; então conto o centro de massa b = (n1 + n2 + n3 + n4) / 4. Bem, o vetor de curvatura final pode ser calculado como c = vb, não é nada como
diferenças finitas comuns para a segunda derivada .

Diretamente no código, fica assim:
std::vector<Vec3f> curvature(verts.size(), Vec3f(0,0,0)); for (int i=0; i<(int)verts.size(); i++) { for (int j=0; j<(int)vvadj[i].size(); j++) { curvature[i] = curvature[i] - verts[vvadj[i][j]]; } curvature[i] = verts[i] + curvature[i] / (float)vvadj[i].size(); }
Bem, fazemos o seguinte várias vezes (veja a figura anterior): movemos o vértice v para v: = b + const * c. Observe que, se a constante for igual a um, nosso vértice não se moverá em lugar algum! Se a constante for zero, o vértice será substituído pelo centro de massa dos vértices vizinhos, o que suavizará nossa superfície. Se a constante for maior que a unidade (a imagem do título foi feita usando const = 2.1), o vértice mudará na direção do vetor de curvatura da superfície, reforçando os detalhes. É assim que fica no código:
for (int it=0; it<100; it++) { for (int i=0; i<(int)verts.size(); i++) { Vec3f bary(0,0,0); for (int j=0; j<(int)vvadj[i].size(); j++) { bary = bary + verts[vvadj[i][j]]; } bary = bary / (float)vvadj[i].size(); verts[i] = bary + curvature[i]*2.1;
A propósito, se for menor que a unidade, os detalhes serão enfraquecidos pelo contrário (const = 0,5), mas isso não será equivalente à simples suavização, o "contraste da imagem" permanecerá:

Observe que meu código gera um arquivo de modelo 3D no formato
.obj do Wavefront , renderizado em um programa de terceiros. Você pode ver o modelo resultante, por exemplo, no
visualizador online . Se você está interessado nos métodos de renderização, em vez de gerar o modelo, leia meu
curso sobre computação gráfica .
Exemplo 3: adicionando restrições
Vamos voltar ao primeiro exemplo e fazer exatamente a mesma coisa, mas não reescrevemos os elementos da matriz com os números 0, 18 e 31:
import matplotlib.pyplot as plt x = [0.] * 32 x[0] = x[31] = 1. x[18] = 2. plt.plot(x, drawstyle='steps-mid') for iter in range(1000): for i in range(len(x)): if i in [0,18,31]: continue x[i] = (x[i-1]+x[i+1])/2. plt.plot(x, drawstyle='steps-mid') plt.show()
Inicializei o restante, elementos "livres" da matriz com zeros e ainda os substitui iterativamente pelo valor médio dos elementos vizinhos. É assim que a evolução da matriz se parece nas primeiras cento e cinquenta iterações:

É bastante óbvio que desta vez a solução convergirá não para um elemento constante que preenche a matriz, mas para duas rampas lineares. A propósito, é realmente óbvio para todos? Caso contrário, experimente esse código, especificamente, dou exemplos com um código muito curto, para que você possa entender completamente o que está acontecendo.
Digressão lírica: solução numérica de sistemas de equações lineares.
Nos seja dado o sistema usual de equações lineares:

Ele pode ser reescrito, deixando em cada uma das equações em um lado do sinal de igual x_i:
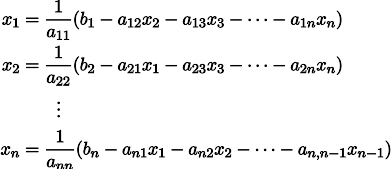
Nos seja dado um vetor arbitrário

aproximando a solução de um sistema de equações (por exemplo, zero).
Colocando-o no lado direito do sistema, podemos obter um vetor de aproximação da solução atualizado

.
Para esclarecer, x1 é obtido de x0 da seguinte maneira:
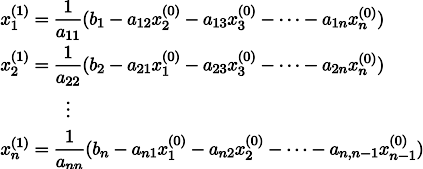
Repetindo o processo k vezes, a solução será aproximada pelo vetor
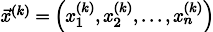
Por via das dúvidas, escreva uma fórmula de recursão:
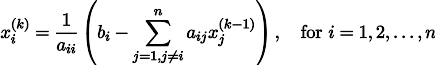
Sob algumas suposições sobre os coeficientes do sistema (por exemplo, é óbvio que os elementos diagonais não devem ser zero, porque os dividimos), esse procedimento converge para a verdadeira solução. Essa ginástica é conhecida na literatura como
método de Jacobi . Certamente, existem outros métodos para resolver numericamente sistemas de equações lineares e muito mais poderosos, por exemplo,
o método do gradiente conjugado , mas, talvez, o método Jacobi seja um dos mais simples.
Exemplo 3 novamente, mas por outro lado
E agora vamos dar uma olhada no loop principal do Exemplo 3:
for iter in range(1000): for i in range(len(x)): if i in [0,18,31]: continue x[i] = (x[i-1]+x[i+1])/2.
Comecei com um vetor inicial x e atualizo-o mil vezes, e o procedimento de atualização é similarmente suspeito ao método Jacobi! Vamos escrever este sistema de equações explicitamente:

Demore um pouco, verifique se cada iteração no meu código Python é estritamente uma atualização do método Jacobi para esse sistema de equações. Os valores x [0], x [18] e x [31] são fixos para mim, respectivamente, eles não estão incluídos no conjunto de variáveis e, portanto, são transferidos para o lado direito.
No total, todas as equações em nosso sistema se parecem com - x [i-1] + 2 x [i] - x [i + 1] = 0. Essa expressão nada mais é do que
diferenças finitas comuns para a segunda derivada . Ou seja, nosso sistema de equações simplesmente prescreve que a segunda derivada deve ser igual a zero em todos os lugares (bem, exceto no ponto x [18]). Lembre-se, eu disse que é óbvio que as iterações devem convergir para rampas lineares? É precisamente por isso que a derivada linear da segunda derivada é zero.
Você sabia que acabamos de resolver
o problema de Dirichlet para a equação de Laplace ?
A propósito, um leitor atento deve ter notado que, estritamente falando, no meu código, os sistemas de equações lineares são resolvidos não pelo método Jacobi, mas
pelo método Gauss-Seidel , que é uma espécie de otimização do método Jacobi:
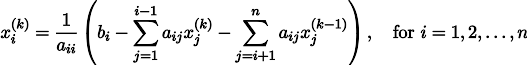
Exemplo 4: Equação de Poisson
E vamos mudar um pouco o terceiro exemplo: cada célula é colocada não apenas no centro de massa das células vizinhas, mas no centro de massa
mais alguma constante (arbitrária): import matplotlib.pyplot as plt x = [0.] * 32 x[0] = x[31] = 1. x[18] = 2. plt.plot(x, drawstyle='steps-mid') for iter in range(1000): for i in range(len(x)): if i in [0,18,31]: continue x[i] = (x[i-1]+x[i+1] +11./32**2 )/2. plt.plot(x, drawstyle='steps-mid') plt.show()
No exemplo anterior, descobrimos que colocar no centro de massa é a discretização do operador Laplace (no nosso caso, a segunda derivada). Ou seja, agora estamos resolvendo um sistema de equações que diz que nosso sinal deve ter uma segunda derivada constante. A segunda derivada é a curvatura da superfície; portanto, uma função quadrática por partes deve ser a solução para o nosso sistema. Vamos verificar a amostragem em 32 amostras:
Com um comprimento de matriz de 32 elementos, nosso sistema converge para uma solução em algumas centenas de iterações. Mas e se tentarmos uma matriz de 128 elementos? Tudo é muito mais triste aqui, o número de iterações já deve ser calculado em milhares:
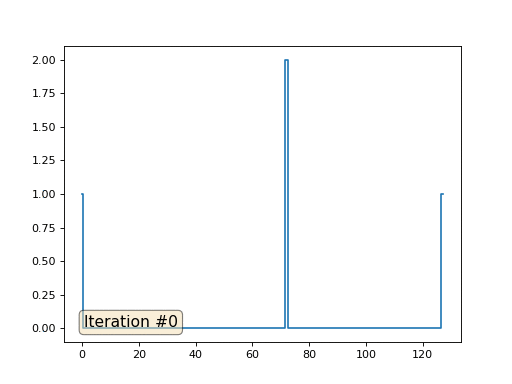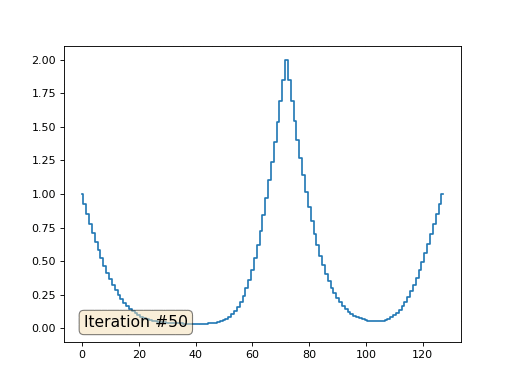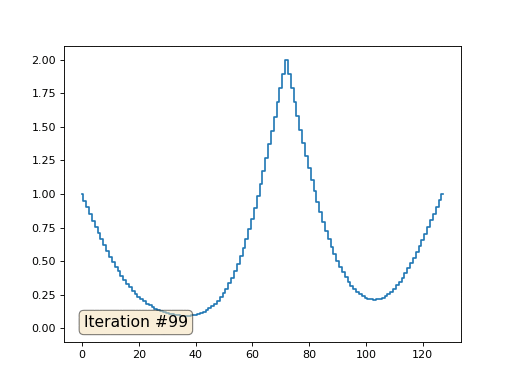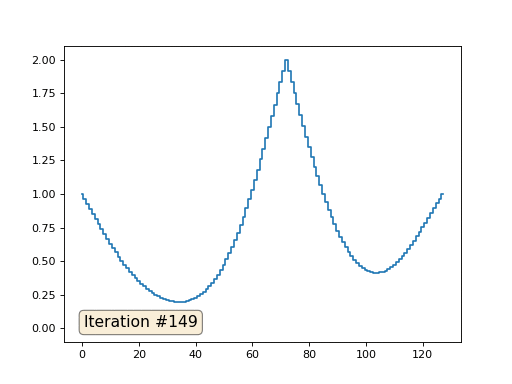
O método de Gauss-Seidel é extremamente simples de programar, mas não aplicável a grandes sistemas de equações. Você pode tentar acelerar, usando, por exemplo,
métodos multigrid . Em palavras, isso pode parecer complicado, mas a idéia é extremamente primitiva: se queremos uma solução com uma resolução de mil elementos, podemos primeiro resolver com dez elementos, obter uma aproximação aproximada, depois duplicar a resolução, resolvê-la novamente e assim por diante, até alcançarmos resultado desejado. Na prática, fica assim:
E você não pode se exibir e usar solucionadores reais de sistemas de equações. Então, resolvo o mesmo exemplo construindo a matriz A e a coluna b e resolvendo a equação da matriz Ax = b:
import numpy as np import matplotlib.pyplot as plt n=1000 x = [0.] * n x[0] = x[-1] = 1. m = n*57//100 x[m] = 2. A = np.matrix(np.zeros((n, n))) for i in range(1,n-2): A[i, i-1] = -1. A[i, i] = 2. A[i, i+1] = -1. A = A[1:-2,1:-2] A[m-2,m-1] = 0 A[m-1,m-2] = 0 b = np.matrix(np.zeros((n-3, 1))) b[0,0] = x[0] b[m-2,0] = x[m] b[m-1,0] = x[m] b[-1,0] = x[-1] for i in range(n-3): b[i,0] += 11./n**2 x2 = ((np.linalg.inv(A)*b).transpose().tolist()[0]) x2.insert(0, x[0]) x2.insert(m, x[m]) x2.append(x[-1]) plt.plot(x2, drawstyle='steps-mid') plt.show()
E aqui está o resultado do trabalho deste programa, observe que a solução acabou instantaneamente:

Assim, de fato, nossa função é quadrática por partes (a segunda derivada é constante). No primeiro exemplo, definimos a segunda segunda derivada como zero, a terceira não-zero, mas a mesma em todos os lugares. E o que estava no segundo exemplo? Resolvemos a
equação discreta de Poisson especificando a curvatura da superfície. Deixe-me lembrá-lo do que aconteceu: calculamos a curvatura da superfície de entrada. Se resolvermos o problema de Poisson definindo a curvatura da superfície na saída igual à curvatura da superfície na entrada (const = 1), nada mudará. O fortalecimento das características faciais ocorre quando simplesmente aumentamos a curvatura (const = 2,1). E se const <1, a curvatura da superfície resultante diminui.
Atualização: outro brinquedo como lição de casa
Desenvolvendo a ideia sugerida pelo
SquareRootOfZero , brinque com este código:
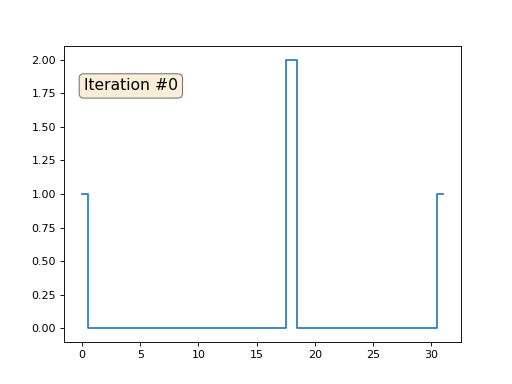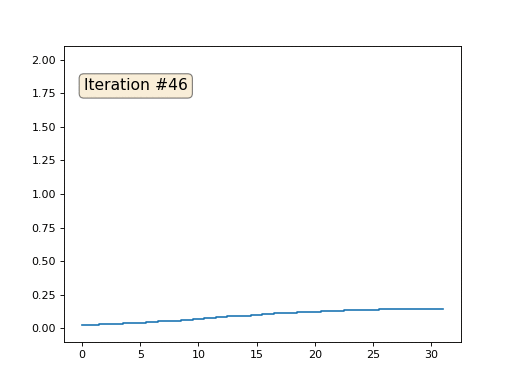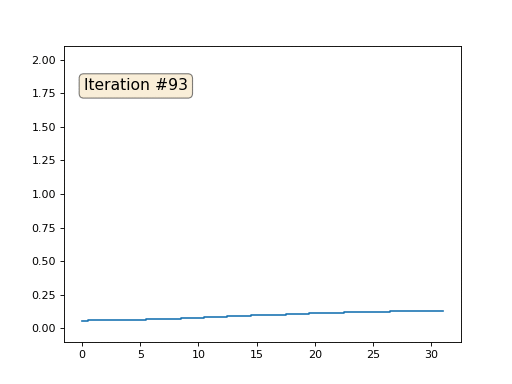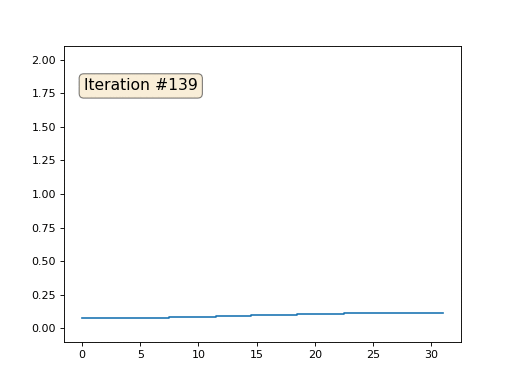
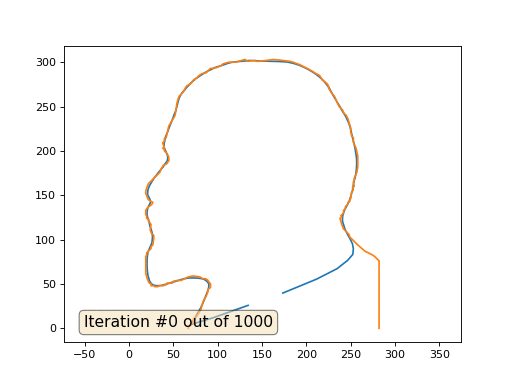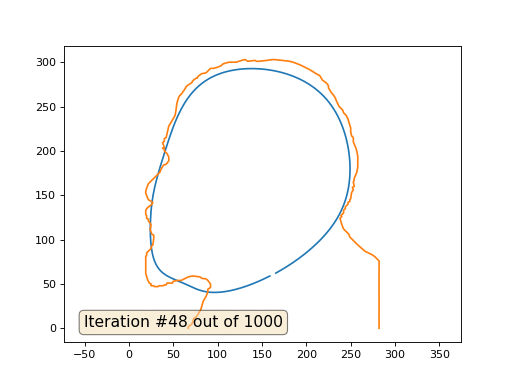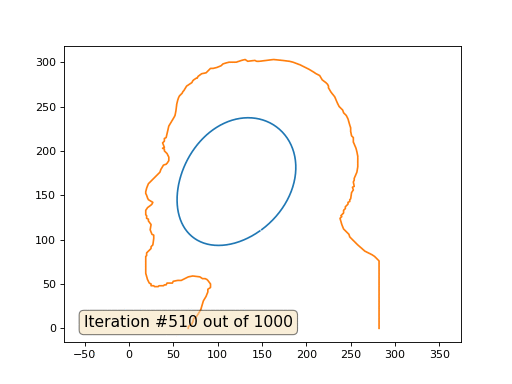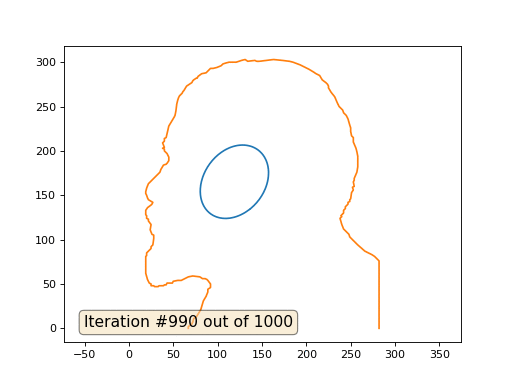
Texto oculto import numpy as np import matplotlib.pyplot as plt import matplotlib.animation as animation fig, ax = plt.subplots() x = [282, 282, 277, 274, 266, 259, 258, 249, 248, 242, 240, 238, 240, 239, 242, 242, 244, 244, 247, 247, 249, 249, 250, 251, 253, 252, 254, 253, 254, 254, 257, 258, 258, 257, 256, 253, 253, 251, 250, 250, 249, 247, 245, 242, 241, 237, 235, 232, 228, 225, 225, 224, 222, 218, 215, 211, 208, 203, 199, 193, 185, 181, 173, 163, 147, 144, 142, 134, 131, 127, 121, 113, 109, 106, 104, 99, 95, 92, 90, 87, 82, 78, 77, 76, 73, 72, 71, 65, 62, 61, 60, 57, 56, 55, 54, 53, 52, 51, 45, 42, 40, 40, 38, 40, 38, 40, 40, 43, 45, 45, 45, 43, 42, 39, 36, 35, 22, 20, 19, 19, 20, 21, 22, 27, 26, 25, 21, 19, 19, 20, 20, 22, 22, 25, 24, 26, 28, 28, 27, 25, 25, 20, 20, 19, 19, 21, 22, 23, 25, 25, 28, 29, 33, 34, 39, 40, 42, 43, 49, 50, 55, 59, 67, 72, 80, 83, 86, 88, 89, 92, 92, 92, 89, 89, 87, 84, 81, 78, 76, 73, 72, 71, 70, 67, 67] y = [0, 76, 81, 83, 87, 93, 94, 103, 106, 112, 117, 124, 126, 127, 130, 133, 135, 137, 140, 142, 143, 145, 146, 153, 156, 159, 160, 165, 167, 169, 176, 182, 194, 199, 203, 210, 215, 217, 222, 226, 229, 236, 240, 243, 246, 250, 254, 261, 266, 271, 273, 275, 277, 280, 285, 287, 289, 292, 294, 297, 300, 301, 302, 303, 301, 301, 302, 301, 303, 302, 300, 300, 299, 298, 296, 294, 293, 293, 291, 288, 287, 284, 282, 282, 280, 279, 277, 273, 268, 267, 265, 262, 260, 257, 253, 245, 240, 238, 228, 215, 214, 211, 209, 204, 203, 202, 200, 197, 193, 191, 189, 186, 185, 184, 179, 176, 163, 158, 154, 152, 150, 147, 145, 142, 140, 139, 136, 133, 128, 127, 124, 123, 121, 117, 111, 106, 105, 101, 94, 92, 90, 85, 82, 81, 62, 55, 53, 51, 50, 48, 48, 47, 47, 48, 48, 49, 49, 51, 51, 53, 54, 54, 58, 59, 58, 56, 56, 55, 54, 50, 48, 46, 44, 41, 36, 31, 21, 16, 13, 11, 7, 5, 4, 2, 0] n = len(x) cx = x[:] cy = y[:] for i in range(0,n): bx = (x[(i-1+n)%n] + x[(i+1)%n] )/2. by = (y[(i-1+n)%n] + y[(i+1)%n] )/2. cx[i] = cx[i] - bx cy[i] = cy[i] - by lines = [ax.plot(x, y)[0], ax.text(0.05, 0.05, "Iteration #0", transform=ax.transAxes, fontsize=14,bbox=dict(boxstyle='round', facecolor='wheat', alpha=0.5)), ax.plot(x, y)[0] ] def animate(iteration): global x, y print(iteration) for i in range(0,n): x[i] = (x[(i-1+n)%n]+x[(i+1)%n])/2. + 0.*cx[i]
Este é o resultado padrão, Lenin vermelho é o dado inicial, a curva azul é sua evolução, no infinito o resultado converge para um ponto:
E aqui está o resultado com o coeficiente 2:

Lição de casa: por que, no segundo caso, Lenin primeiro se transforma em Dzerzhinsky e depois converge novamente para Lenin, mas de tamanho maior?
Conclusão
Muitas tarefas de processamento de dados, em particular geometria, podem ser formuladas como uma solução para um sistema de equações lineares. Neste artigo, não contei
como construir esses sistemas, meu objetivo era apenas mostrar que isso é possível. O tópico do próximo artigo não será "por que", mas "como" e quais solucionadores serão usados posteriormente.
A propósito, e afinal no título do artigo, há menos quadrados. Você os viu no texto? Se não, então isso não é absolutamente assustador, esta é exatamente a resposta para a pergunta "como?". Fique na linha, no próximo artigo mostrarei exatamente onde eles estão escondidos e como modificá-los para obter acesso a uma ferramenta de processamento de dados extremamente poderosa. Por exemplo, em dez linhas de código, você pode obter o seguinte:

Fique ligado para mais!