Melhorando a qualidade dos panoramas de colagem combinando o gráfico de transformações projetivas

Olá Habr! Hoje falaremos sobre uma das maneiras de melhorar a qualidade dos panoramas de colagem. Existe uma abordagem amplamente usada para colar panoramas de objetos planos, mas como essa abordagem não apresenta desvantagens, oferecemos nossa melhoria.

A tarefa do panorama é criar uma imagem composta com base em um conjunto de imagens de origem (veja a Fig. 1). Encontra aplicação na solução de problemas práticos como:

• som da superfície da Terra a partir de um satélite ou de um drone;
• colando imagens obtidas usando um microscópio;
• colando vídeo;
• Captura de imagem em super resolução.

Figura 1 - Imagens originais e panorama

Em geral, o algoritmo de colagem de panorama pode ser formulado da seguinte maneira [1] (veja a Fig. 2). No início, é necessário extrair um número suficiente de quadros do fluxo de vídeo. Isso pode ser feito on-line, lendo seqüencialmente todos os quadros e selecionando quadros individuais com a frequência necessária.

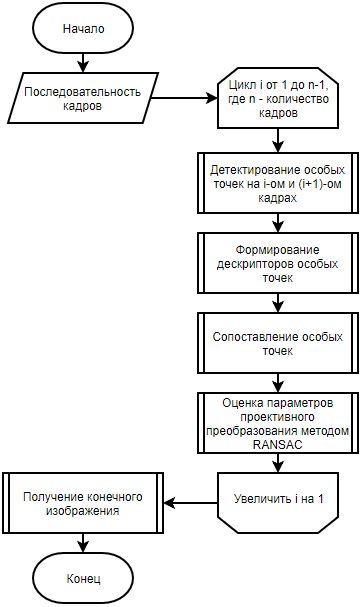
Figura 2 - O fluxograma do algoritmo de colagem de panorama usando pontos especiais

Depois disso, classificando sequencialmente pares de imagens do conjunto, é necessário detectar pontos singulares e calcular seus descritores nessas imagens [2–4]. São esses pontos singulares que possibilitam construir uma correspondência geométrica entre dois quadros. A seguir, é apresentada uma comparação de pontos singulares com base em seus descritores. Deve-se ter em mente que isso não exclui a possibilidade de obter correspondências falsas.

Além disso, tendo dois conjuntos de pontos singulares, deve-se encontrar uma transformação projetiva que traduza da melhor maneira os pontos de um quadro para os pontos correspondentes do outro. Para resolver esse problema, a abordagem RANSAC pode ser usada [5]. Essa abordagem é descrita em mais detalhes em [6, 7]

Para procurar uma transformação projetiva entre os quadros, também pode ser usado um fluxo óptico, que é frequentemente usado na tarefa de colar panoramas [8].
Após obter o conjunto desejado de transformações projetivas, ocorre um procedimento técnico para colar imagens, a saber: para cada pixel do panorama final (x, y) para cada canal (RGB), a média aritmética das intensidades de pixel é calculada com as coordenadas (x, y) de todos os quadros, incluindo um pixel com essas coordenadas.

Usando os métodos de busca de transformações projetivas, pode-se determinar o deslocamento da posição da câmera em relação à posição anterior no espaço. Em condições de laboratório, a precisão do cálculo desses dados é suficiente para construir um panorama de um objeto estacionário plano. Em condições reais, ao calcular o deslocamento da posição da câmera em relação à posição anterior, surge um erro de cálculo (erro de medição / interferência / limitações impostas por algoritmos, etc.). Com o tempo, o erro acumulativo continua aumentando de tal maneira que, apesar da precisão aceitável de determinar o deslocamento entre as posições adjacentes, o panorama geral do objeto já contém desvios sérios (veja a Fig. 3).

Figura 3 - Erro acumulativo

Estabelecemos o objetivo de desenvolver um método para combinar o gráfico de transformações projetivas para a tarefa de aplicar objetos fixos planos e resistentes ao problema de acumular erros. Outro objetivo é desenvolver o método de forma que não dependa do método de cálculo dos parâmetros da transformação projetiva.

Uma das condições deve ser atendida:

• fotografar um objeto pseudo-rígido fixo;
• tiro de um objeto próximo ao plano a uma distância suficientemente grande;
• para todas as posições da câmera durante o disparo, o requisito é atendido: para todos os pontos da imagem, os raios que conectam esses pontos ao foco da câmera não coincidem.

Descrição do algoritmo de correspondência do gráfico de transformação de projeção

Introduzimos o conceito de um único sistema de coordenadas. Por um único sistema de coordenadas, queremos dizer um sistema de coordenadas em que os mesmos pontos de um objeto de imagens diferentes terão as mesmas coordenadas. Este requisito pode ser expresso pela seguinte fórmula:

$$

$$f (x) = y,$$

onde $$$f$É um mapeamento definido na parte comum dos quadros e traduzindo os pontos do primeiro quadro nos pontos do segundo quadro, $$$x$- coordenadas do ponto no sistema de coordenadas do primeiro quadro, $$$y$- coordenadas de um ponto no sistema de coordenadas do segundo quadro.

No caso em que o mapeamento $$$f$Se você pode continuar corretamente além da interseção de quadros, podemos complementar o segundo quadro com informações do primeiro. Assim, um mapa colado como um mosaico de dois ou mais quadros será obtido.

Depois de encontrar as transformações projetivas entre os quadros adjacentes, existe uma colagem inicial que define a localização exclusiva dos quadros em um único sistema de coordenadas (veja a Fig. 4).

Figura 4 - A localização inequívoca do quadro no mapa

Depois de construir a colagem primária de imagens, é construído um gráfico de transformações projetivas $$$G$:

$$

$$G = (V, E),$$

onde $$$V$- muitos quatros pontos, que são os vértices das imagens projetadas corrigidas; $$$\ vert V \ vert = n$, $$$E$- muitas transformações projetivas entre quadros; $$$\ vert E \ vert = m$.

Uma aresta entre os vértices é construída apenas se os quadros se cruzarem pelo menos a $$$T \%$na colagem primária (IoU - interseção sobre a união) (ver Fig. 5, 6):

$$

$$\ frac {s_ {ij}} {s_i + s_j-s_ {ij}} \ cdot100 \%> T \%.$$

Figura 5 - Área de interseção do quadro

Limiar $$$T$ele é selecionado dependendo do método usado para procurar uma transformação projetiva, equilibrando entre a condicionalidade da tarefa de procurar uma transformação projetiva entre dois quadros e o número esperado desejado de arestas e ciclos no gráfico.

Figura 6 - Um exemplo de construção de gráfico

Como resultado, o gráfico de transformações projetivas $$$G$tem a seguinte aparência (veja a Fig. 7):

Figura 7 - O gráfico final das transformações projetivas

Se o gráfico contiver ciclos (consulte a Fig. 6), aparecerão informações redundantes, que também podem conter contradições. Para determinar que tipo de contradição pode surgir, consideramos um certo ciclo do gráfico (veja a Fig. 8). Deixe este ciclo consistir em vértices $$ . Depois, temos uma série de mapeamentos projetivos ao longo deste ciclo:

$$

$$H_ {12}: 1 \ to2, \\ H_ {23}: 2 \ to3, \\ ... \\ H_ {k1}: k \ to1. \\ $$

Considere a composição desses mapeamentos:

$$

$$H_ {k1} * ... * H_ {23} * H_ {12} = H_ {11}.$$

Figura 8 - Loop gráfico

Exibição $$$H_ {11}$deve ser um mapeamento idêntico. Se o mapeamento $$$H_ {11}$diferente do idêntico, então dizemos que é obtida uma contradição. Nesse caso, o ciclo será chamado de inconsistente . Assim, existe um problema associado à presença de ciclos inconsistentes no gráfico dos mapeamentos projetivos, pois com perfeita colagem das contradições no gráfico das transformações projetivas $$$G$deve estar ausente.

Descrevemos o algoritmo de correspondência para o gráfico de transformações projetivas, ou seja, combinando todos os seus ciclos. Para minimizar o erro acumulativo que ocorre quando o ciclo é fechado no gráfico de transformações projetivas, é utilizado o conceito do método SLAM (Localização e Mapeamento Simultâneos) [9].

Considere em cada quadro quatro pontos na posição geral. Deixe os quadros serem numerados de $$$1$antes $$$n$então quatro pontos serão indicados por $$$p_i$onde $$$1 \ le i \ le n$. Esse conjunto de quatro pontos $$$P$define exclusivamente um sistema de coordenadas único, pois para quaisquer dois quadros, é possível encontrar exclusivamente um mapa projetivo que converte um quatro pontos em outro.

Para encontrar o conjunto de quatro pontos que determinará o gráfico consistente desejado, você pode usar o método dos mínimos quadrados. Minimizamos o funcional, que é igual à soma de todas as arestas do conjunto $$$E$contar $$$G$e para cada aresta - a soma de quatro pontos de quantidades $$$\ Vert H_ {ij} p_ {is} -p_ {js} \ Vert$. Para encontrar uma solução que minimize o funcional, propõe-se o uso do método do gradiente conjugado.

$$

$$\ sum _ {(i, j) \ em E} \ sum_ {s = 1} ^ 4 \ Vert H_ {ij} p_ {é} -p_ {js} \ Vert \ to \ min_ {P}.$$

Depois de haver uma transformação projetiva para cada quadro que define exclusivamente a posição do quadro no mapa, você pode obter uma imagem panorâmica.

Resultados experimentais

Até o momento, não existe um método universal para avaliar a qualidade das imagens coladas. Como regra, a qualidade da colagem é avaliada organoléptica por especialistas, mas, para pesquisas científicas, é preferível ter uma avaliação quantitativa da qualidade, calculada automaticamente.

Para avaliar a qualidade da colagem sem a participação de um especialista humano, é necessário ter uma colagem padrão com a qual o resultado será comparado. A abordagem na qual a colagem foi obtida de um vídeo real e a fotografia de todo o objeto é considerada como colagem padrão requer boas condições de laboratório, usando um manipulador capaz de fixar fisicamente (usando sensores) a posição da câmera no espaço. No entanto, esse método de avaliação da qualidade é caro.

Em [10], para quantificar a qualidade da colagem de panorama, usando uma imagem de alta resolução, eles propõem a criação de um vídeo artificial cujos quadros são áreas distorcidas projetivamente da imagem original (veja a Fig. 9). Distorcida projetivamente todos os quadros, exceto o primeiro, pois um único sistema de coordenadas é especificado em relação ao primeiro quadro. Além disso, esses quadros de vídeo artificial são colados em um panorama, que é comparado com a imagem de referência original. Com essa abordagem, é possível evitar problemas com a diferença de brilho das colas obtidas e de referência, além de distorção da cena.

Figura 9 - Imagem original e quadros de vídeo artificial

Para comparar a qualidade da colagem antes e depois de concordar em um gráfico, uma amostra de teste de 50 imagens foi preparada, 50 vídeos artificiais foram criados a partir das imagens originais, de acordo com a qual a colagem foi realizada (consulte a Fig. 10). Todos os panoramas obtidos foram reduzidos ao tamanho das imagens de origem e, para cada panorama, a medida de erro foi calculada:

$$

$$RMSE = \ sqrt {\ frac {\ sum_ {i = 1} ^ h \ sum_ {j = 1} ^ w ((I_ {ij} ^ R- \ hat {I_ {ij} ^ R}) ^ 2+ (I_ {ij} ^ G- \ hat {I_ {ij} ^ G}) ^ 2+ (I_ {ij} ^ B- \ hat {I_ {ij} ^ B}) ^ 2)} {h \ cdot w \ cdot 3}},$$

onde $$$h$- altura da imagem $$$w$- largura da imagem $$$I_ {ij} ^ R$- intensidade de pixel $$$(i, j)$o panorama resultante no canal vermelho ( $$$G$- canal verde $$$B$- canal azul) $$$\ hat {I_ {ij} ^ R}$- intensidade de pixel $$$(i, j)$imagem de origem no canal vermelho ( $$$G$- canal verde $$$B$- canal azul).

Figura 10 - Panorama antes da concordância do gráfico (RMSE = 35.3) e depois (RMSE = 14.2)

Na representação gráfica, o RMSE no conjunto de testes é o seguinte (veja a Fig. 11):

Figura 11 - RMSE na amostra de teste. Os quadros são classificados em ordem crescente do RMSE até a correspondência do gráfico.

De acordo com cada valor-raiz do erro quadrático médio da raiz antes da correspondência, são apresentados os valores-raiz do erro quadrático médio da raiz após a correspondência do gráfico. O valor médio do RMSE na amostra de teste antes que o gráfico seja consistente é 35,5 , depois da correspondência do gráfico - 13,9 .

Conclusão

Com base nos resultados da comparação da qualidade da colagem, podemos concluir que combinar o gráfico reduz significativamente o erro acumulado e melhora a qualidade dos panoramas da colagem. No entanto, deve-se ter em mente que a correspondência de gráficos só pode ajudar se houver ciclos no gráfico de transformações projetivas. Na ausência de ciclos no gráfico de transformações projetivas, o módulo de correspondência de gráficos não prejudica a qualidade da colagem do panorama.

Vale ressaltar que esse método de correspondência de grafos funciona com um conjunto de transformações projetivas, e a maneira como essas transformações projetivas foram encontradas não desempenha um papel importante nesse método.

No futuro, está planejado otimizar a complexidade do algoritmo, uma vez que é aplicável apenas a casos de usuários "offline".

Literatura

[1] Gubin A.Yu., Kovin R.V. Uma abordagem simples para a tarefa de colar imagens sobrepostas em um panorama // X Conferência Internacional Científica e Prática de Estudantes, Estudantes de Graduação e Jovens Cientistas "Juventude e Tecnologias da Informação Modernas", p. 79-81, 2012.
[2] Drummond T., Rosten E. Machine Learning para detecção de cantos em alta velocidade // 9ª Conferência Europeia sobre Visão Computacional (ECCV), p. 430-443, 2006.
[3] Lowe DG Distinctive Image Features de pontos-chave invariáveis ​​em escala // International Journal of Computer Vision, p. 91-110, 2004.
[4] Bay H., Ess A., Yuitelaars T., Van Gool L. SURF: Acelerou recursos robustos // Visão por Computador e Entendimento de Imagem, v. 110, p. 346-359, 2008.
[5] Martin A. Fischler, Robert C. Bolles. Consenso de amostra aleatória: um paradigma para ajuste de modelo com aplicativos para análise de imagem e cartografia automatizada // Comm. do ACM, v. 24, p. 381-395, 1981.
[6] Arlazarov V.L., Bulatov K.B., Chernov T.S. O método de busca de imagens difusas em grandes volumes de dados de vídeo // High Availability Systems, Vol. 12, No. 1, p. 53-58, 2016.
[7] Skoryukina N. et al. Captura de tela: pesquisa de quadros de fluxo de TV com consulta distorcida e ruidosa projetualmente // 9ª Conferência Internacional sobre Visão de Máquina (ICMV) - Proc. SPIE V. 10341, P. 103410Y, 2017.
[8] Bouguet JY Implementação piramidal do rastreador de recursos lucas kanade: destruição do algoritmo // Intel corporation, V. 5, p. 1-10, 2001.
[9] Newman P., Ho K. SLAM-loop de fechamento com características visualmente salientes // IEEE Proc. da Conferência Internacional de Robótica e Automação, p. 635-642, 2005.
[10] Paalanen P., Kamarainen JK, Kalviainen H. Avaliação quantitativa em mosaico baseada em imagem com vídeo artificial // Conferência Escandinava de Análise de Imagem, Springer (Berlim, Heidelberg), p. 470-479, 2009.