Processos de onda em linhas hidráulicas. O básico

Olá Habr!

Em um artigo anterior , falei sobre o método de características, projetado para calcular processos de ondas em linhas hidráulicas. De fato, é claro, os processos de ondas podem ser calculados na mente, você só precisa conhecer a abordagem.

Sob o corte, mostrarei "nos dedos" e com a ajuda de gifs os principais efeitos das ondas. Como exemplo, voltarei a usar a linha hidráulica, mas, na verdade, elas são baseadas quase nas mesmas equações que para linhas acústicas e elétricas. Portanto, mesmo que você não seja hidráulico, pode haver analogias simples para ajudá-lo a entender os processos de ondas em geral.

Cuidado Gifs animados de 15 MB sob o gato!

Então, aqui consideraremos a propagação de ondas planas unidimensionais em uma linha hidráulica. Essa suposição é verdadeira para tubulações longas, cujo comprimento é muitas vezes maior que o diâmetro interno. Por simplicidade, também negligenciamos o atrito por enquanto. Nesse caso, os processos físicos em andamento serão descritos por um par de equações diferenciais parciais:

$$

$$\ frac {\ parcial p} {\ parcial t} + \ rho \; c ^ 2 \ frac {\ parcial v} {\ parcial x} = 0$$

$$

$$\ frac {\ parcial v} {\ parcial t} + \ frac1 \ rho \ frac {\ displaystyle \ parcial p} {\ displaystyle \ parcial x} = 0$$

onde $$$\ rho$- densidade $$$v$- velocidade $$$p$- pressão $$$c$- velocidade do som.

Por hábito, a aparência dessas equações pode assustar, mas, de fato, tudo é simples aqui. A primeira equação nos diz que a pressão aumentará com o tempo se mais líquido entrar no segmento do tubo do que sair (além disso, quanto mais rápido, mais denso e elástico o líquido está no tubo); a segunda equação mostra que, para acelerar um segmento de um líquido, é necessário aplicar uma diferença de pressão (além disso, quanto maior a densidade, mais diferença de pressão deve ser aplicada para acelerar o segmento). I.e. coisas bastante banais são descritas: o fluido é compressível, o fluido tem uma massa.
Deixemos a solução analítica dessas equações para artigos futuros, passemos imediatamente para o exemplo "nos dedos".
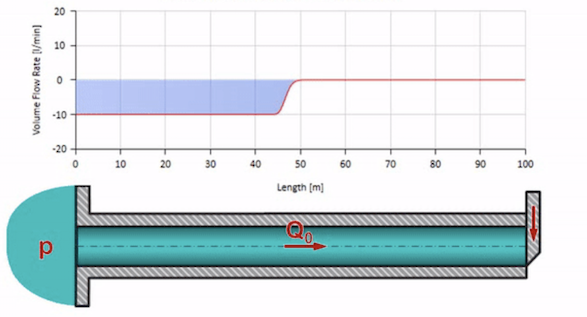
Pegue um tubo cheio de água em que é mantida uma pressão de 100 bar (10 MPa) e uma vazão de 30 l / min. Se um passo de pressão for aplicado na extremidade esquerda, previsivelmente começará a se mover ao longo do fluxo a uma velocidade igual à velocidade do som no meio.

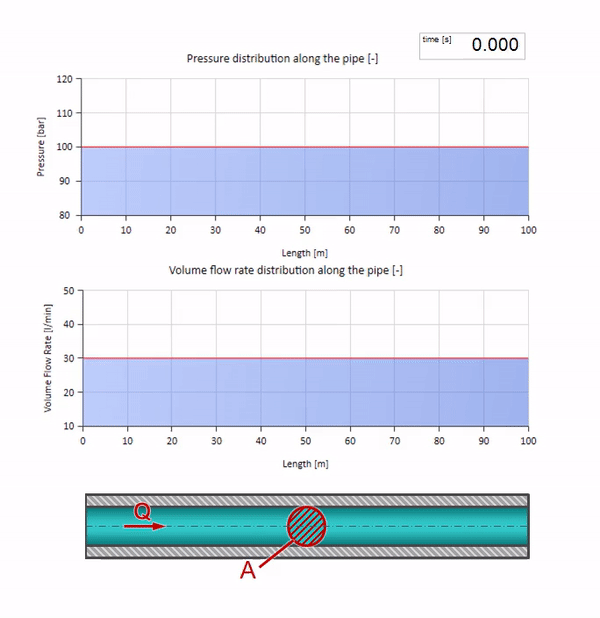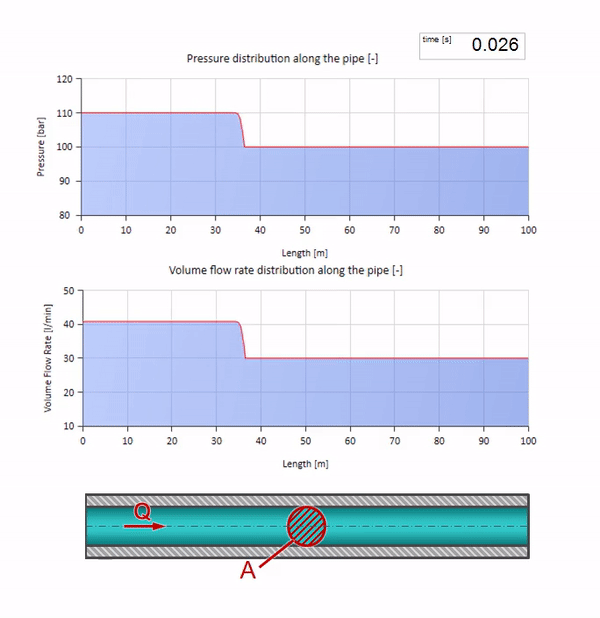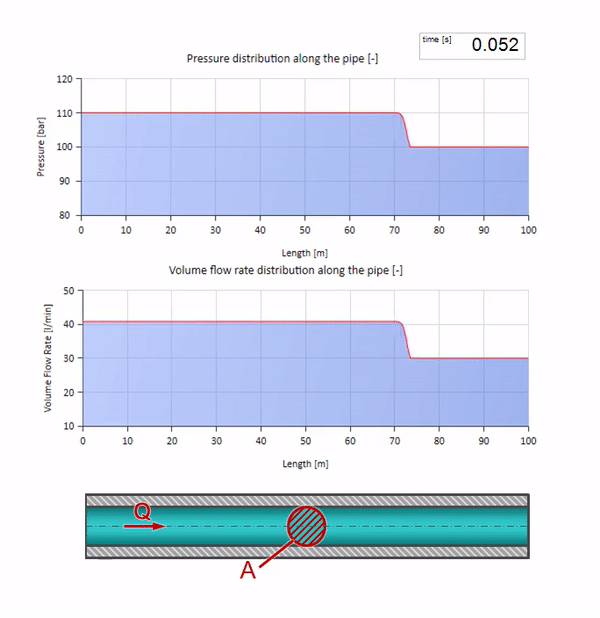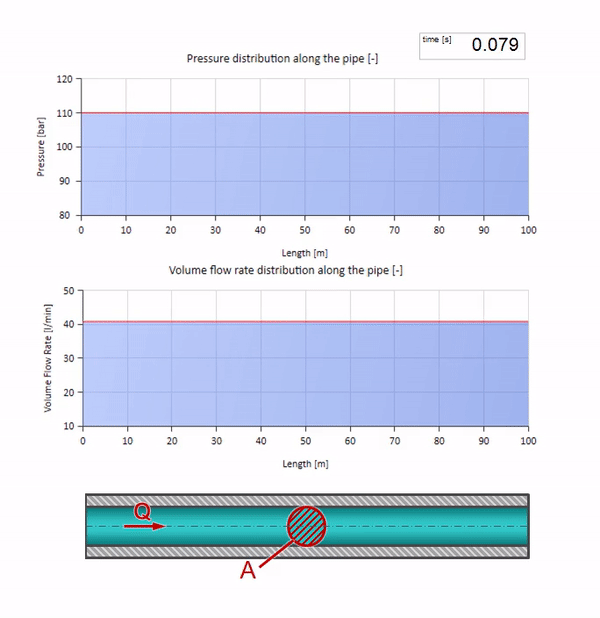
Obviamente, com a pressão, a vazão também mudará. Se a pressão aumentar, ele “ajustará” o fluido a montante e aumentará a taxa de fluxo em alguns “passos” também. Quanto é determinado pelo valor da impedância da onda. Para um tubo com uma área de seção transversal $$$A$preenchido com líquido com densidade $$$\ rho$e velocidade local do som $$$c$, a impedância da onda pode ser calculada da seguinte forma:

$$

$$Z_L = \ frac {\ rho \; c} A$$

Em termos de dimensões, é o mesmo que a resistência hidráulica convencional, usada apenas para calcular as taxas de onda de pressão ( $$$\ widehat p$) e vazão ( $$$\ widehat Q$) e não seus valores absolutos:

$$

$$Z_L = \ frac {\ widehat p} {\ widehat Q}$$

Quanto maior a densidade e a velocidade do som, maior a impedância da onda, ou seja, mais difícil será para uma certa queda de pressão dispersar o líquido (aumentar o fluxo)

Agora vamos ver como duas ondas se moverão, movendo-se uma em direção à outra:

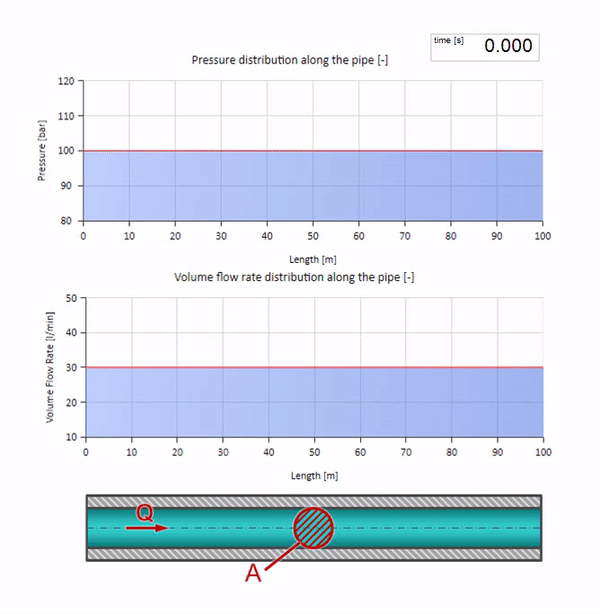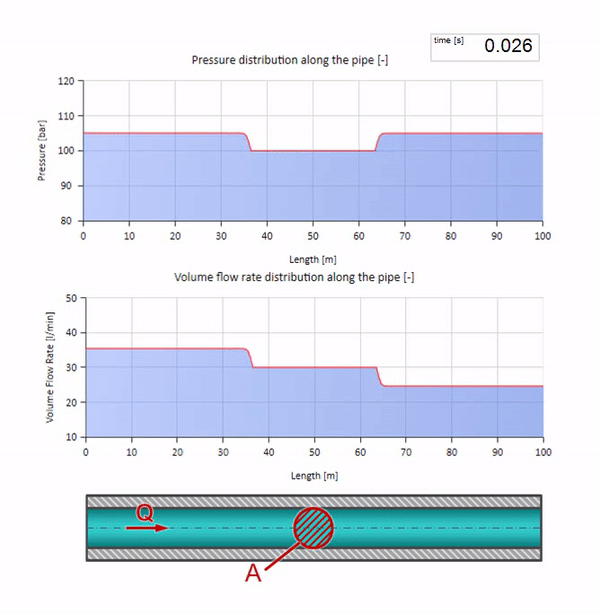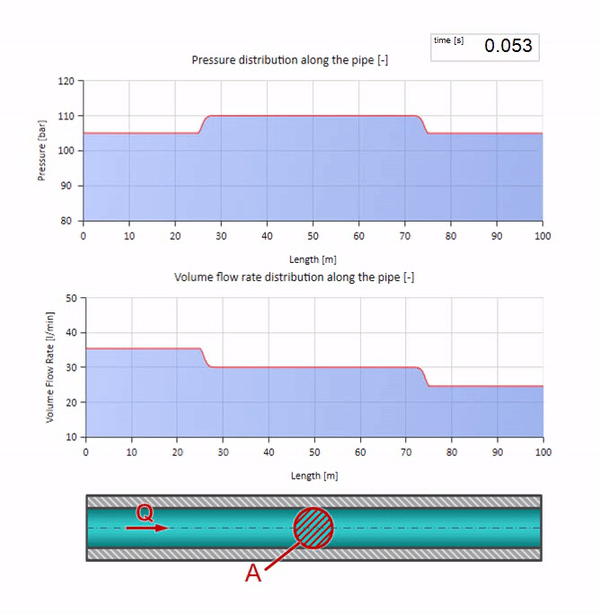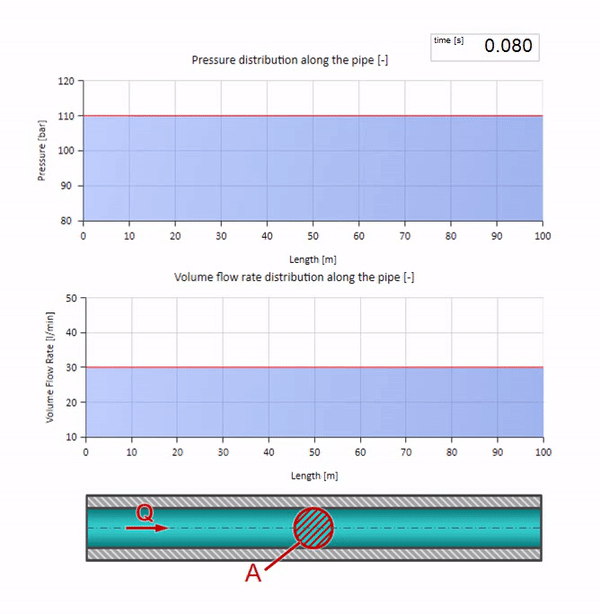
Se a pressão na extremidade direita aumentar, o fluido será inevitavelmente inibido por um diferencial negativo. Isso significa que a onda de aumento de pressão que vai contra o fluxo levará a uma diminuição na taxa de fluxo em uma quantidade determinada novamente pela resistência da onda. Ou seja, uma onda de crescimento de pressão e fluxo em queda se moverá à direita.
Em uma colisão, pode parecer que as ondas de fluxo são refletidas uma da outra e retornam. De fato, eles simplesmente se sobrepõem. Esse efeito também é chamado de interferência:

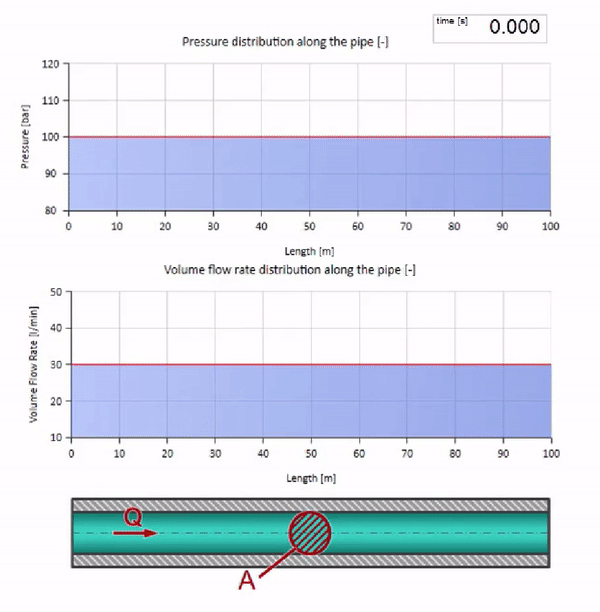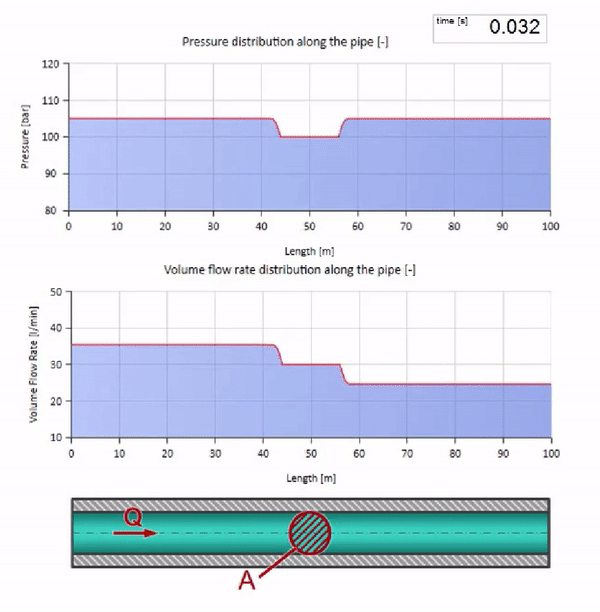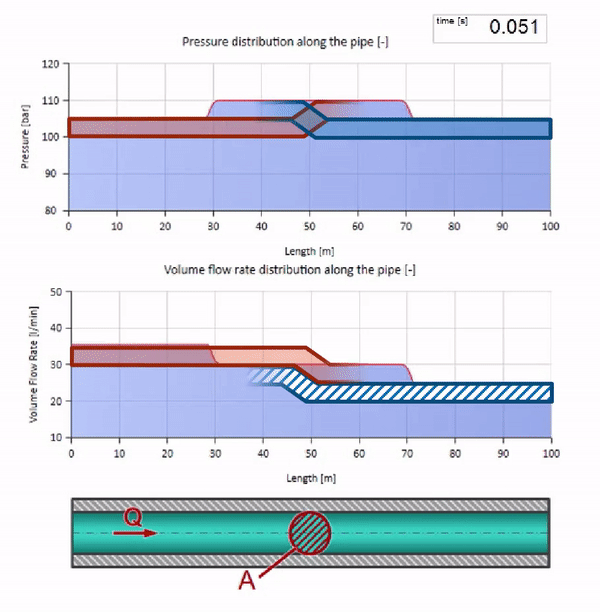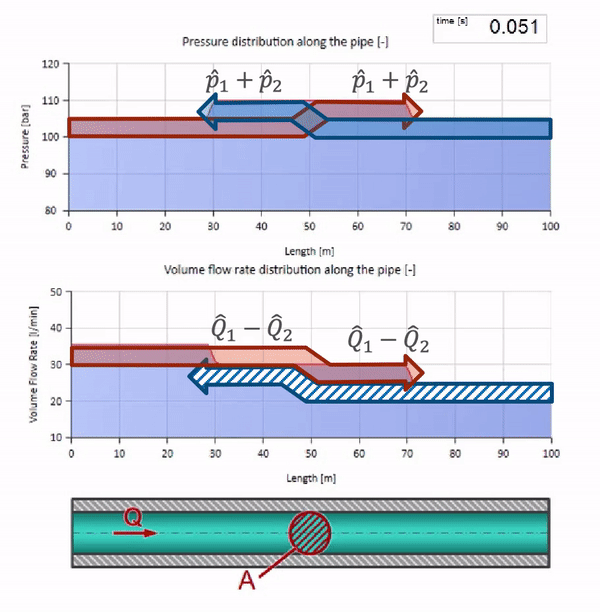
Agora sabemos que cada tubo com um líquido tem uma propriedade como a resistência às ondas. É interessante ver o que acontecerá com a onda se o diâmetro de um tubo em uma determinada seção mudar dramaticamente:

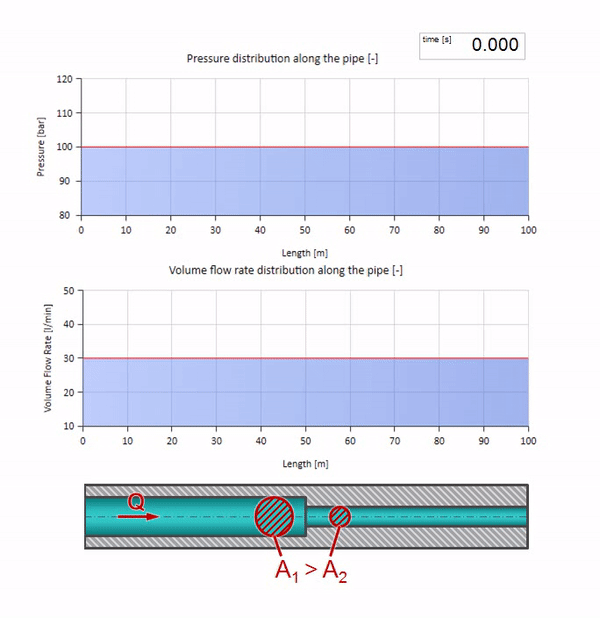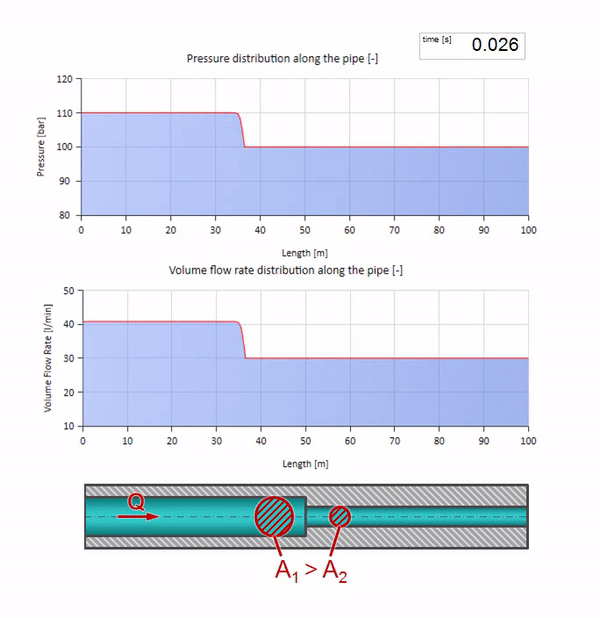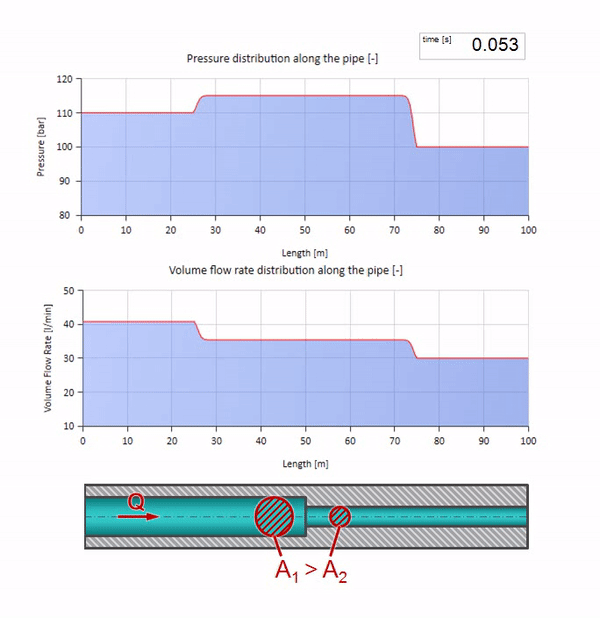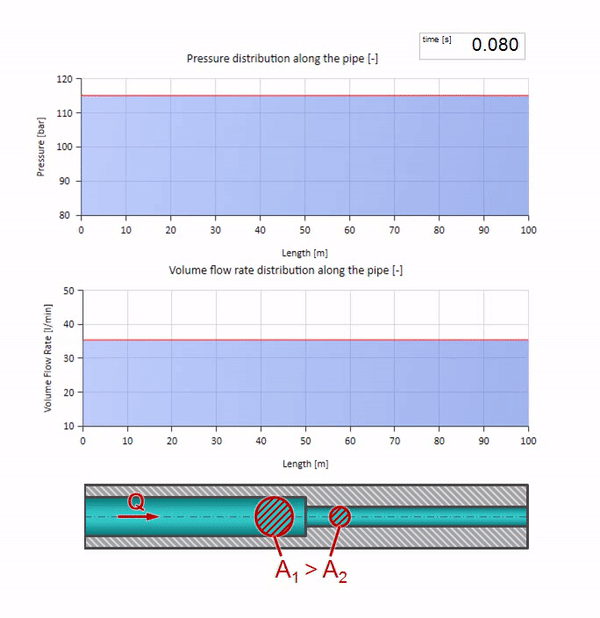
Antes que a onda chegue a um lugar com uma diminuição no diâmetro do tubo, é claro, nada de interessante acontece. Mas, em seguida, atinge uma seção com uma resistência de onda mais alta, o que significa que a proporção da onda de pressão em relação à onda de fluxo deve ser maior do que na seção esquerda do tubo. Isso significa que a onda de pressão deve aumentar e a taxa de fluxo deve diminuir. Ao mesmo tempo, não resta nada para a onda, exceto dobrar-se para a esquerda, mantendo valores iguais na junção dos dois tubos.

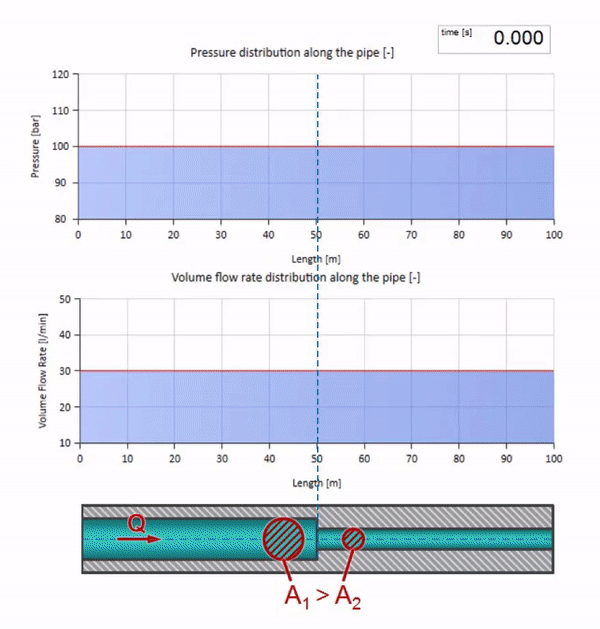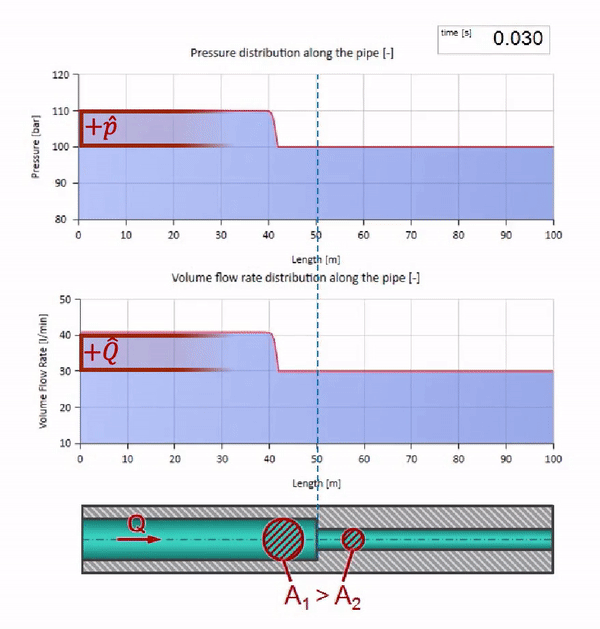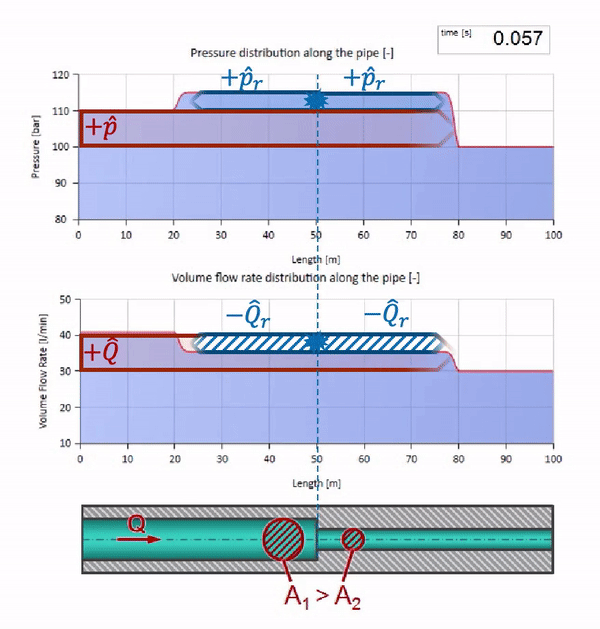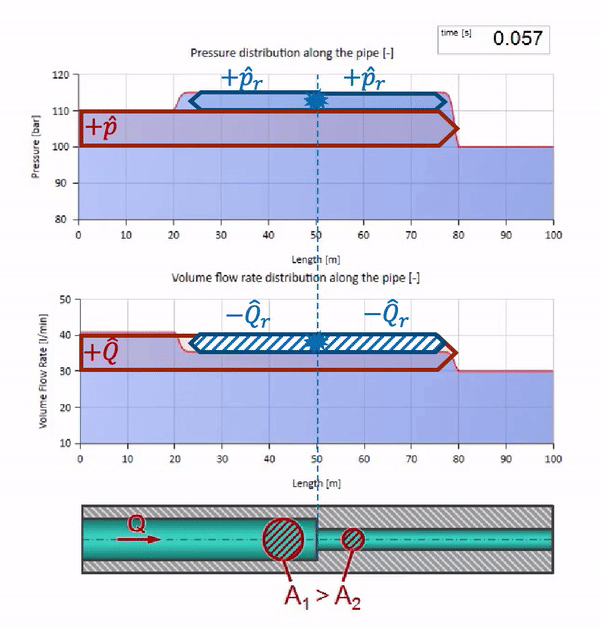
Para cálculos, é conveniente usar o coeficiente de reflexão $$$r$, que é considerado a partir das impedâncias de onda de seções individuais:

$$

$$r = \ frac {Z_2-Z_1} {Z_1 + Z_2}$$

Em seguida, a pressão refletida e as ondas de fluxo podem ser calculadas da seguinte forma:

$$

$${\ widehat p} _r = r \; \ widehat p$$

$$

$${\ widehat Q} _r = - \ frac {\ displaystyle \; {\ widehat p} _r} {Z_1} = - r \; \ widehat Q$$

e essas próprias ondas serão sobrepostas de acordo com a lei de interferência com a original.
E parecerá uma imagem do reflexo de uma onda de um site com menor resistência a ondas:

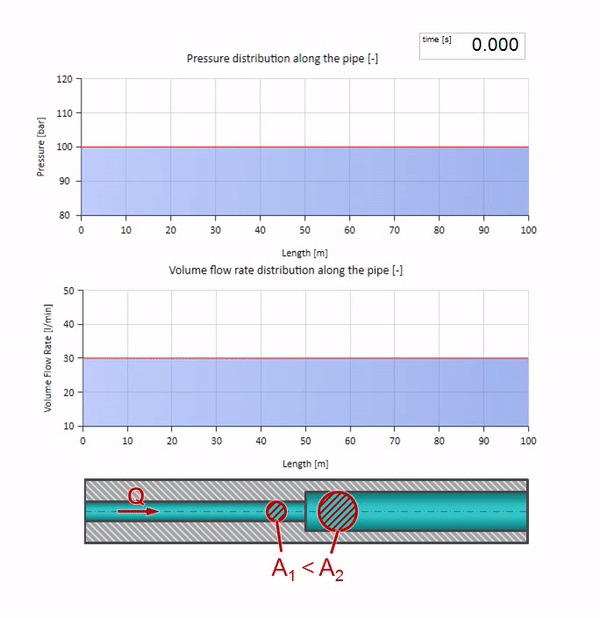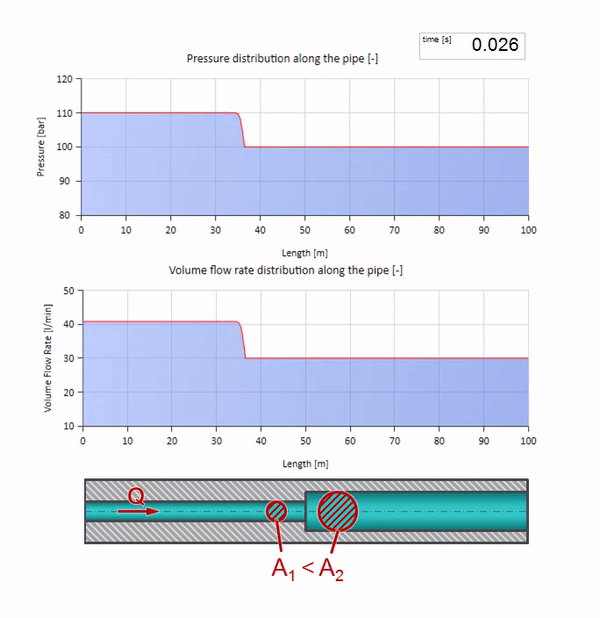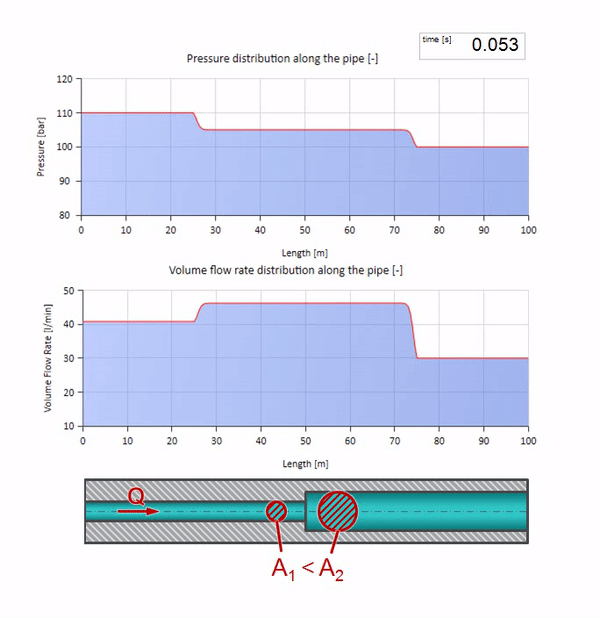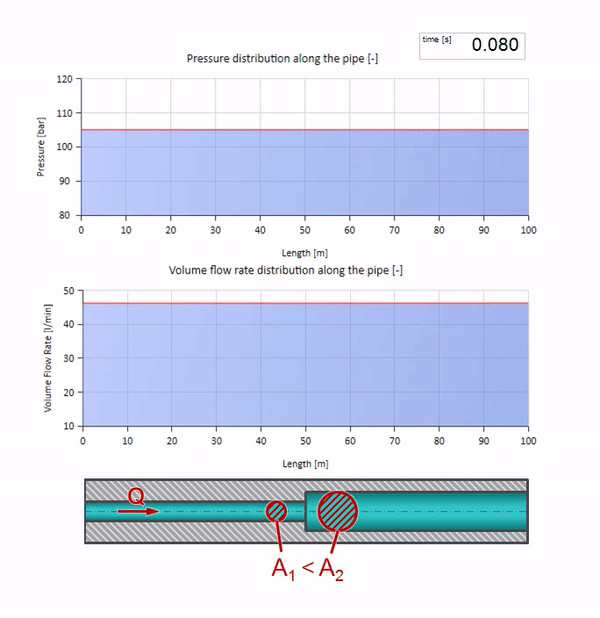
Pode-se observar que desta vez o coeficiente de reflexão é negativo, o que significa que a onda de pressão após a reflexão será menor e a vazão, pelo contrário, mais.

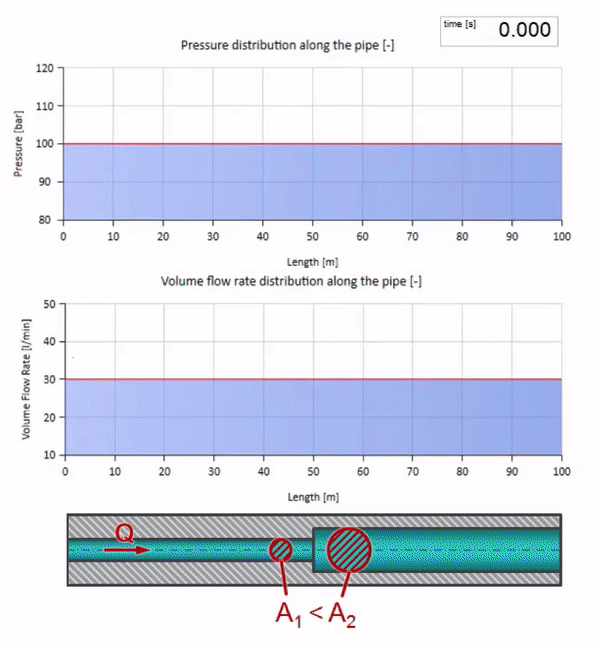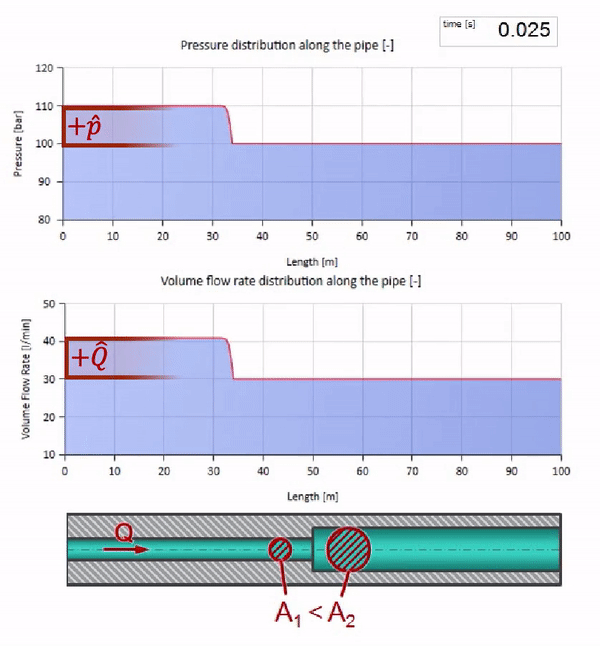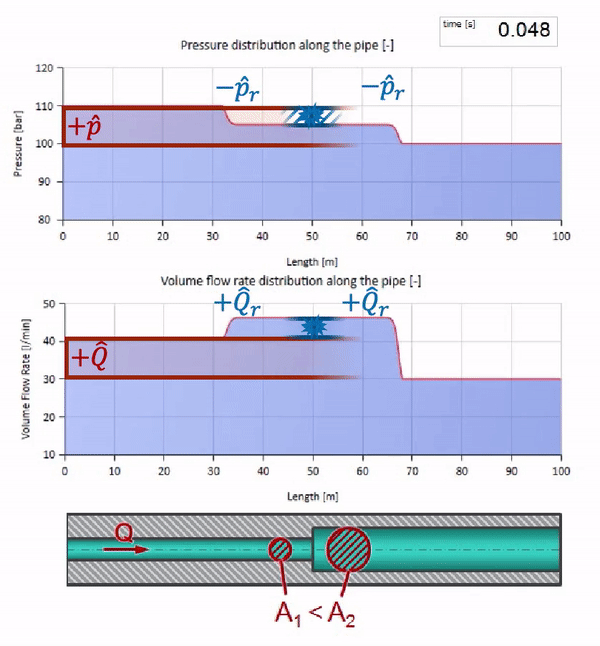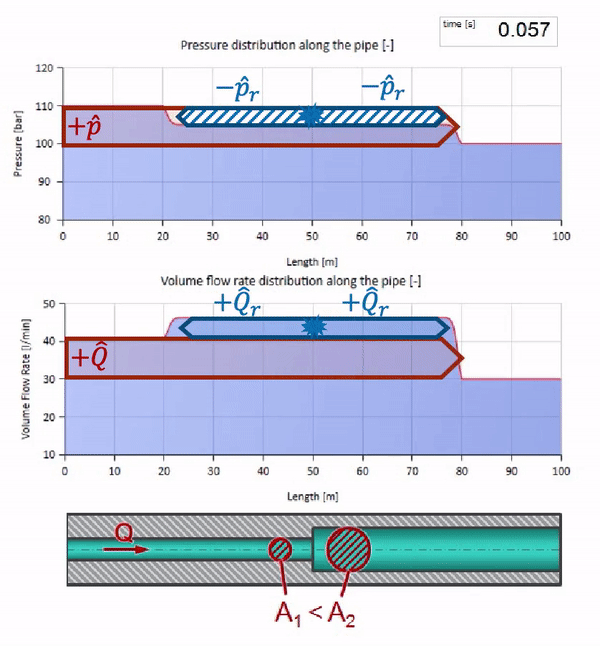
Deve-se lembrar que a impedância depende não apenas do tamanho do tubo, mas também da velocidade local do som. I.e. se tivermos uma seção de tubo com uma luva de borracha na qual a velocidade do som é muito menor, a onda também será refletida:

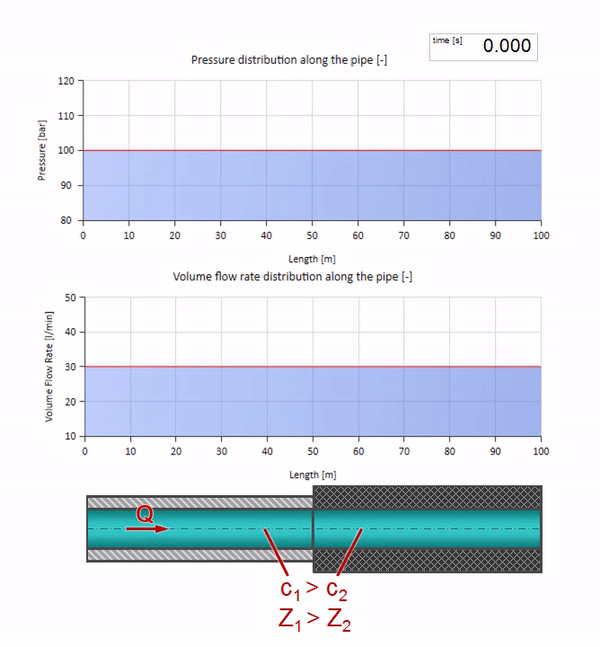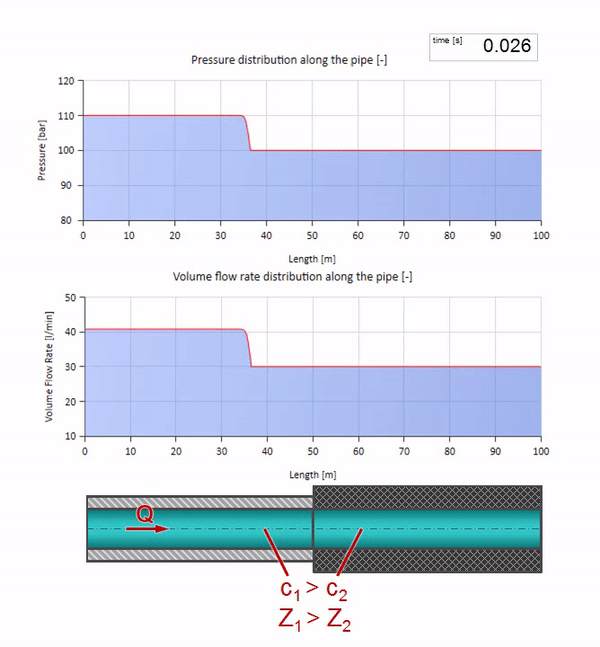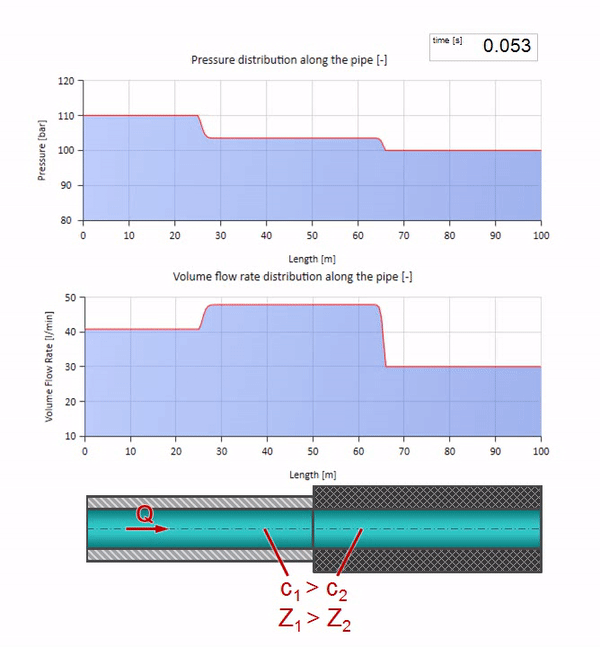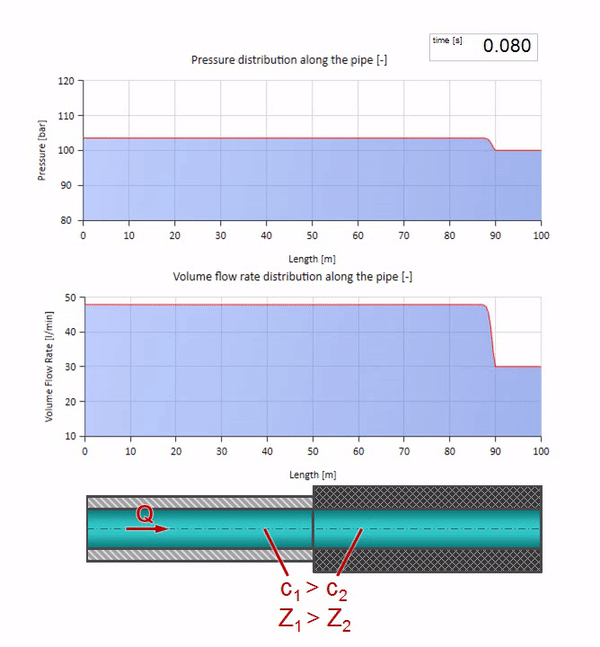
Primeiro, chama a atenção imediatamente que a onda na seção com a parede de borracha do tubo se move mais lentamente. E como a resistência da onda é menor, o resultado da reflexão será semelhante ao caso com a expansão do tubo:

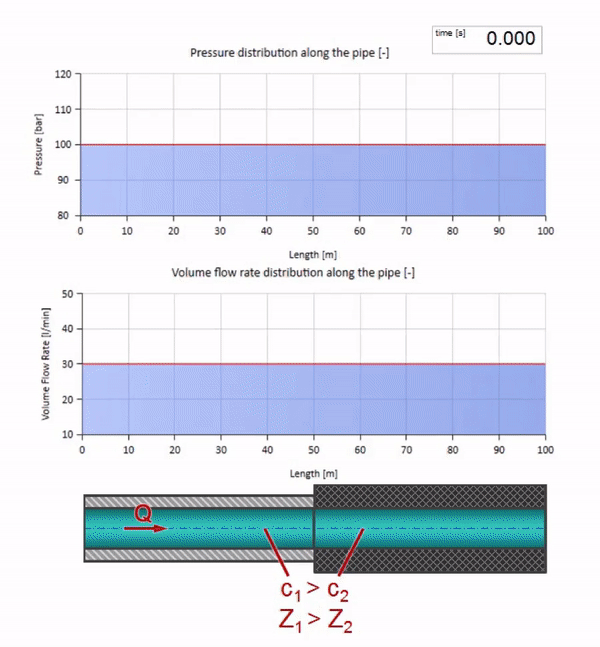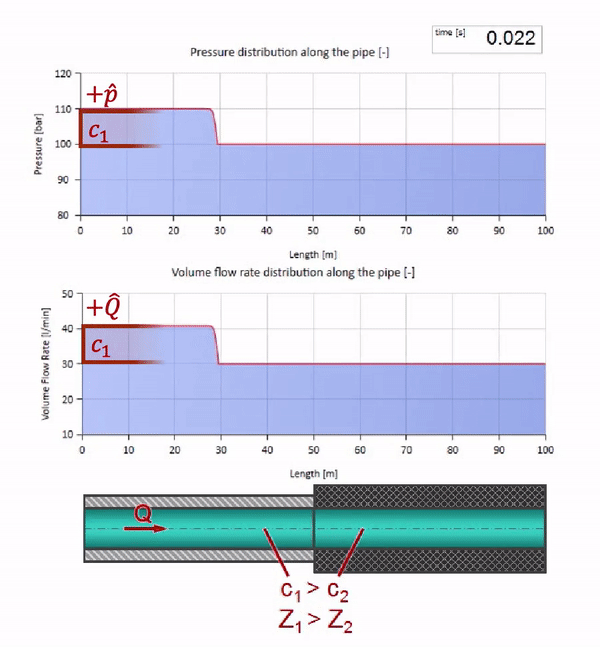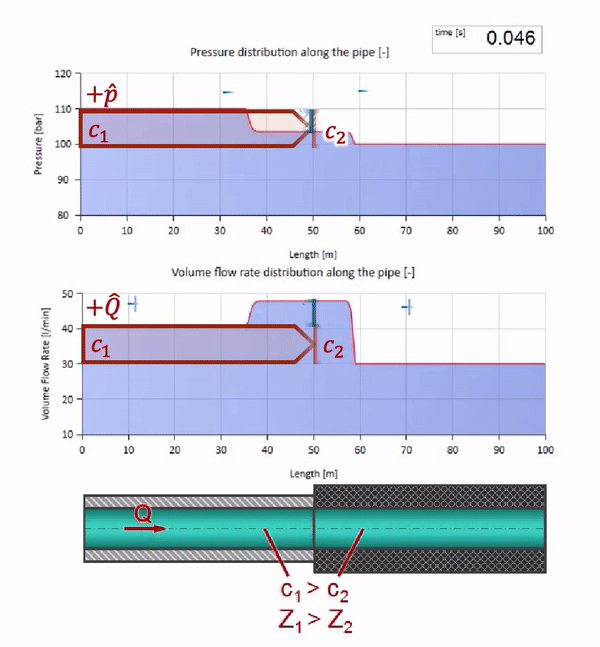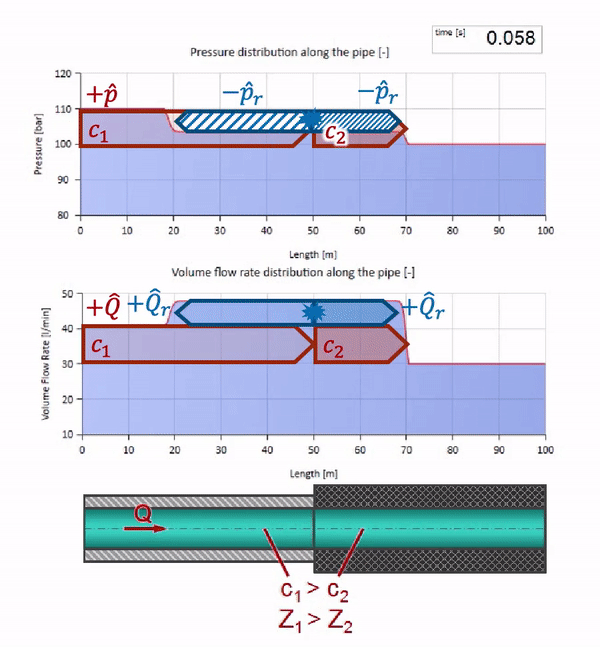
Agora, seria bom considerar casos extremos com valores zero e infinitamente grandes de impedância de onda. Essa será a saída da tubulação para o tanque com pressão constante e a extremidade fechada, respectivamente. Deixarei essas animações sem comentar:


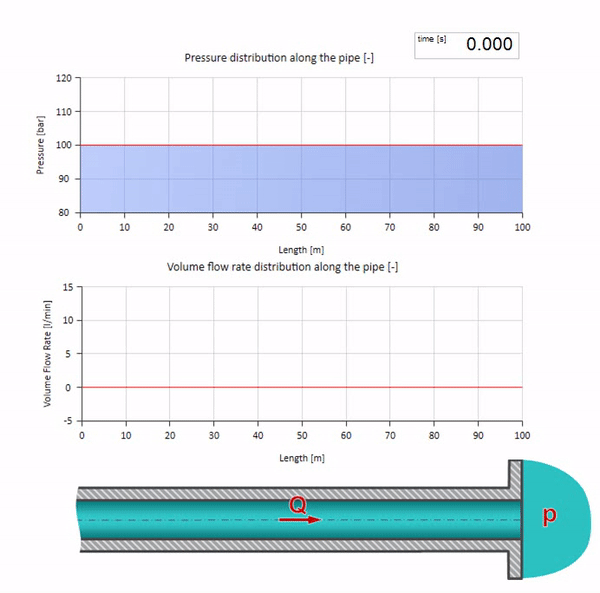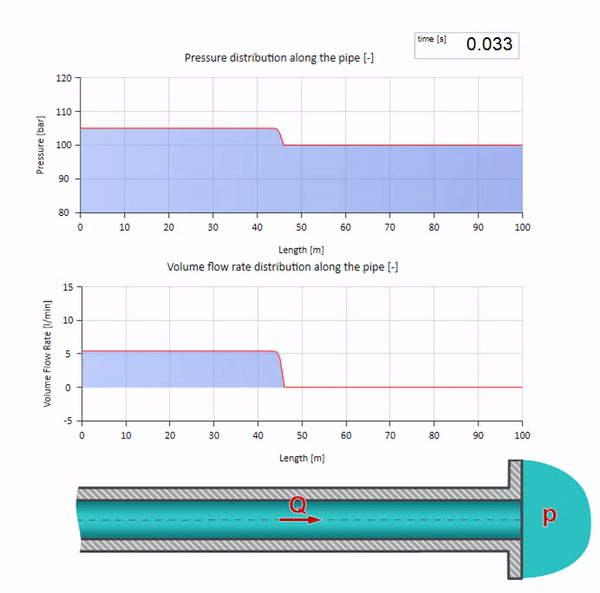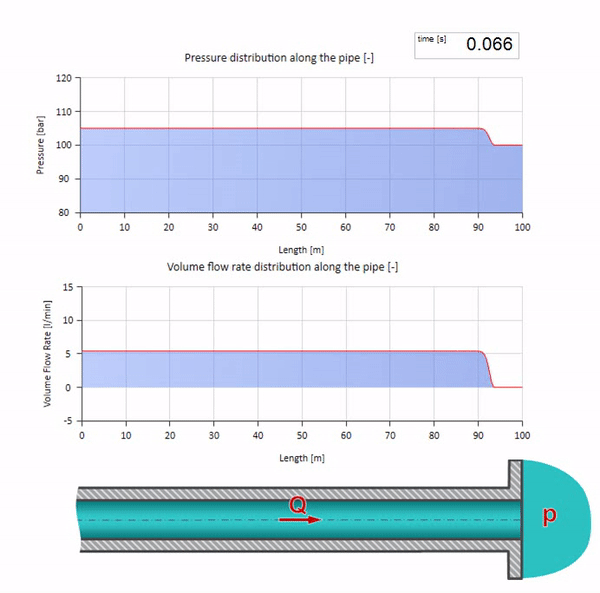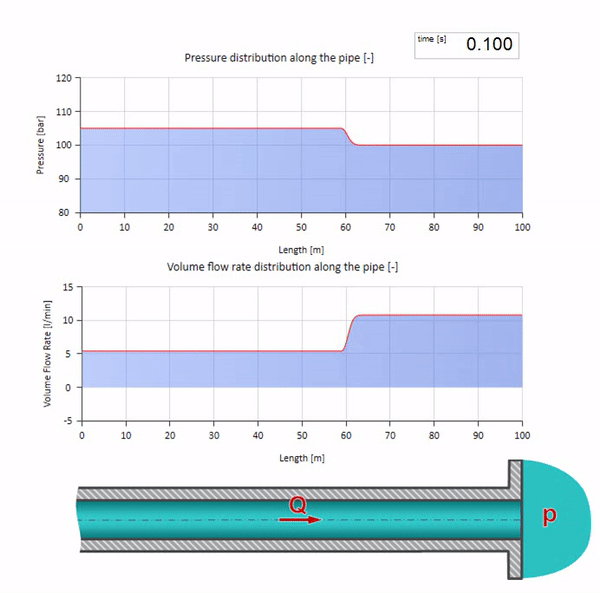
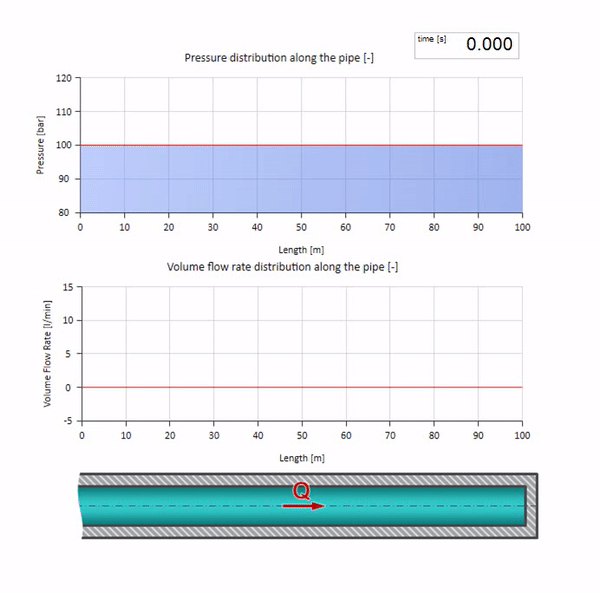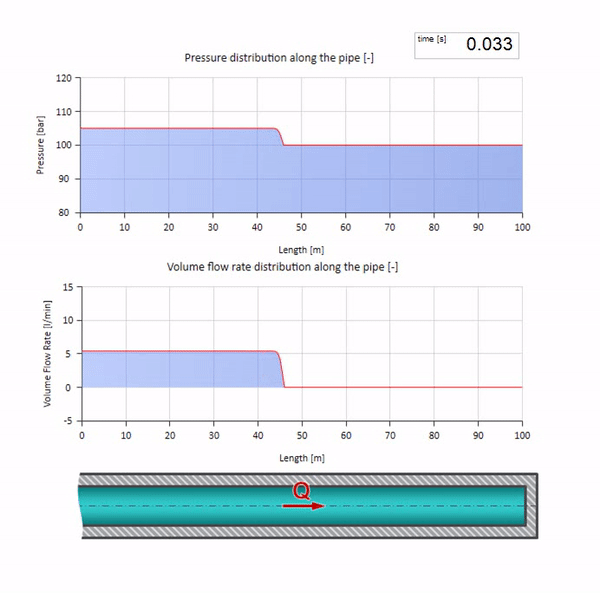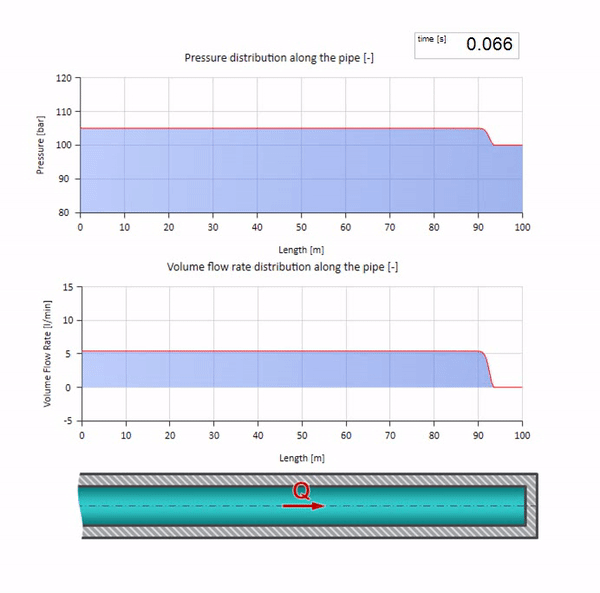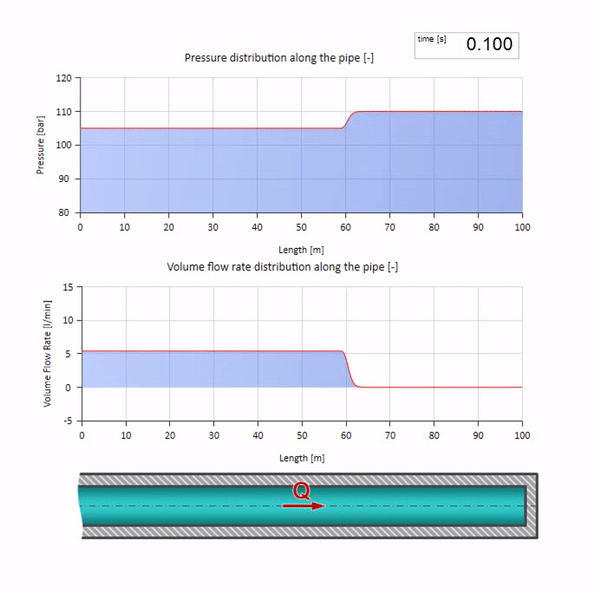
Bem, se combinarmos esses dois casos, obtemos um choque hidráulico clássico:

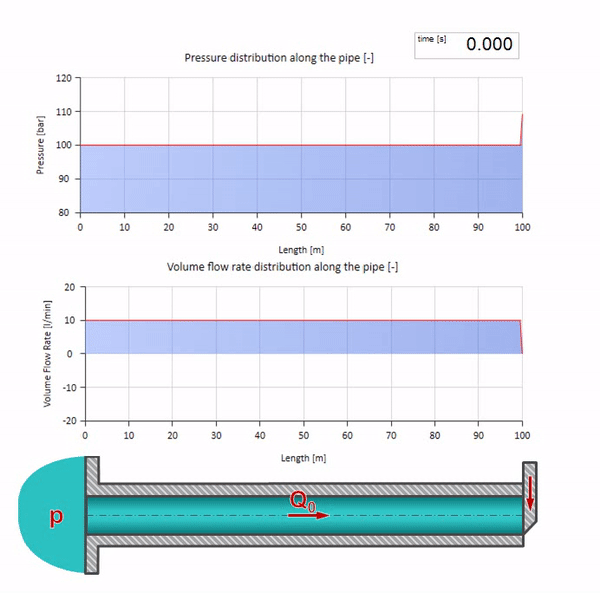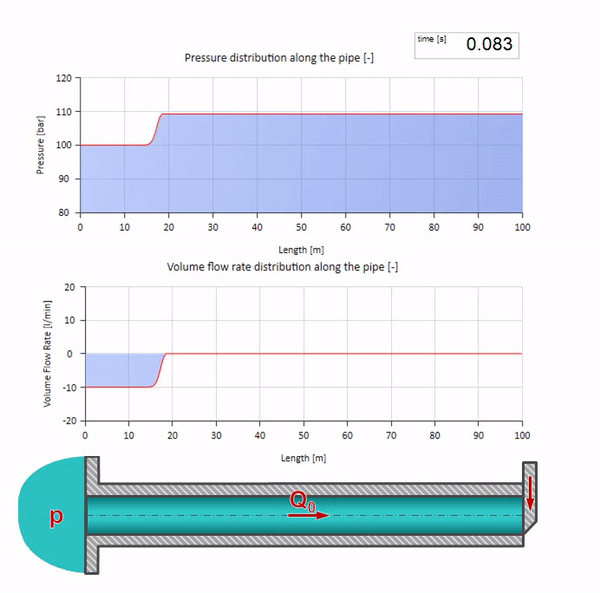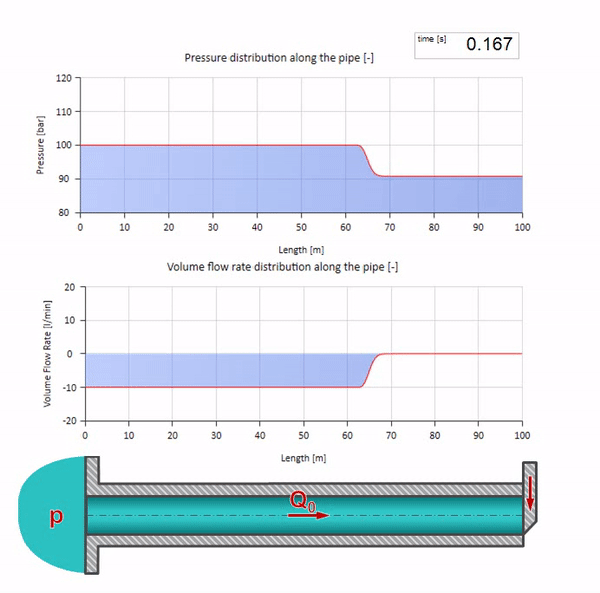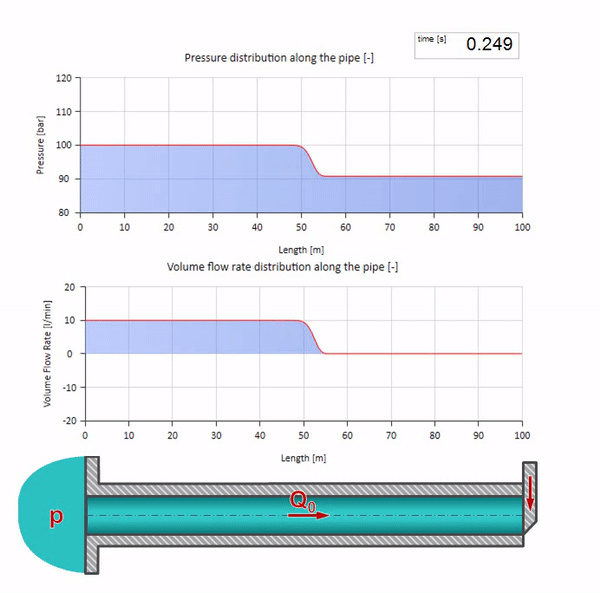
Aqui, no momento inicial do tempo, existe algum valor de fluxo que instantaneamente é igual a zero na extremidade direita do tubo (a válvula fecha). Uma onda de fluxo decrescente e pressão crescente começa a se mover para a esquerda. Essas ondas são refletidas na extremidade direita da tubulação com impedância zero. Na ausência de atrito, esse processo será interminável.
Curiosamente, usando as fórmulas acima, podemos derivar a equação de Zhukovsky para golpe de aríete:

$$

$$\ widehat p = Z_L \ widehat Q \;$$

Expressamos a vazão através da velocidade, assumindo que ela cai de um determinado valor para zero e pintamos a impedância da onda:

$$

$$\ widehat p = A \; v_0 \; \ frac {\ rho \; c} {\ A} = \ rho \; c \; v_0$$

Obtemos o valor do salto de pressão que ocorre quando o obturador é instantaneamente fechado.

Anotações

1. Fui inspirado a escrever um artigo pelo chefe de um livro básico de hidráulica no Departamento de Engenharia Hidráulica da Universidade Técnica de Rach-Westphalian de Aachen, onde, na minha opinião, os processos nas linhas hidráulicas são descritos com mais clareza (Grundlagen der Fluidtechnik Teil 1: Hydraulik, Hubertus Murrenhoff ISBN: 978-3-8440 -1223-1).
2. As animações foram feitas no programa SimulationX, o cálculo foi realizado pelo método de características