Li um livro oficial sobre estratégias de negociação e escrevi meu robô de negociação. Para minha surpresa, o robô não traz milhões, mesmo negociando virtualmente. O motivo é óbvio: um robô, como um carro de corrida, precisa ser "sintonizado", para selecionar parâmetros adaptados a um mercado específico, a um período de tempo específico.
Como o robô possui configurações suficientes, itera todas as combinações possíveis em busca da melhor tarefa que consome muito tempo. Ao mesmo tempo, resolvendo o problema de otimização, não encontrei uma escolha razoável do algoritmo de pesquisa para o vetor quase ótimo dos parâmetros do robô de negociação. Portanto, decidi comparar independentemente vários algoritmos ...
Breve declaração do problema de otimização
Temos um algoritmo de negociação. Dados de entrada - histórico de preços do intervalo horário por 1 ano de observação. Dados de saída - P - lucro ou perda, valor escalar.
O algoritmo de negociação possui 4 parâmetros configuráveis:
- Mf é o período da média móvel "rápida",
- Ms período da média móvel "lenta"
- T - TakeProfit, o nível de lucro desejado para cada transação individual,
- S - StopLoss, o nível de perda alvo para cada transação individual.
Atribuímos um intervalo e uma etapa de alteração fixa para cada um dos parâmetros, um total de
20 valores para cada um dos parâmetros.
Assim, podemos procurar o lucro máximo (P) para um parâmetro em uma matriz de dados de entrada:
- variando um parâmetro, por exemplo, P = f (Ms), produzindo até 20 backtests ,
- variando dois parâmetros, por exemplo, P = f (Ms, T), produzindo até 20 * 20 = 400 backtests,
- variando três parâmetros, por exemplo, P = f (Mf, Ms, T), produzindo até 20 * 20 * 20 = 8.000 backtests,
- variando cada um dos parâmetros, P = f (Mf, Ms, T, S) e produzindo até 20 ^ 4 = 160.000 backtests.
Para a maioria dos algoritmos de negociação, no entanto, são necessárias várias ordens de magnitude mais tempo para realizar um único teste. O que nos leva à tarefa de encontrar um vetor de parâmetros quase ideal, sem a necessidade de iterar todo o conjunto de combinações possíveis.
detalhes sobre robôs comerciais e comerciaisNegociação na bolsa de valores, apostas no centro de negociação de Forex, apostas loucas em "opções binárias", especulação com criptomoedas - uma espécie de "diagnóstico", com várias opções possíveis para o desenvolvimento da "doença". Um cenário muito comum é quando um jogador, depois de jogar "intuição", chega à negociação automática. Não me entenda mal, não quero colocar a ênfase de tal maneira que robôs de negociação rigorosos "tecnologicamente e matematicamente" se oponham à negociação "manual" ingênua e impotente. Por exemplo, eu mesmo estou convencido de que qualquer uma de minhas tentativas de extrair lucro de um mercado eficiente (lido em qualquer mercado transparente e líquido) por meio de especulações, sejam discricionárias ou totalmente automatizadas, está fadada ao fracasso a priori. Se, talvez, não permitir o fator de sorte aleatória.
Entretanto, negociar e, em particular, negociar algo (rítmico), é um hobby popular para muitos. Alguns programam robôs de negociação independentemente, outros vão ainda mais longe e criam suas próprias plataformas para escrever, depurar e testar estratégias de negociação, enquanto outros baixam / compram um "especialista" eletrônico pronto. Mas mesmo aqueles que não escrevem algoritmos de negociação por conta própria devem ter uma idéia de como lidar com essa "caixa preta" para lucrar com isso de acordo com a ideia do autor. Para não ser infundado, faço minhas observações adicionais usando um exemplo de uma estratégia de negociação simples:
Robô de negociação simples
Um robô de negociação analisa a dinâmica do valor do ouro, em dólares por onça troy, e decide "comprar" ou "vender" uma certa quantidade de ouro. Para simplificar, assumimos que o robô sempre negocia em uma onça troy.
Por exemplo, no momento da compra, o custo de uma onça troy de ouro era 1075,00
USD . No momento da venda subsequente (fechamento da transação), o preço aumentou para 1079,00 USD. O lucro dessa transação foi de 4 USD.
Se o robô "vender" ouro a 1075,00 USD e, posteriormente, concluir (fechar) a transação "comprando" ouro de volta a um preço de 1079 USD, o lucro da transação será negativo - menos 4 USD. Na verdade, não importa para nós como o robô vende ouro, o que não possui, para depois "recomprá-lo". Um corretor / centro de negociação permite que um comerciante "compre" e "venda" um ativo de uma maneira ou de outra, ganhando (ou, mais frequentemente, perdendo), com a diferença de taxas.
Decidimos os
dados de entrada para o robô - essa é, de fato, a série temporal de preços (cotações) do ouro. Se você diz que meu exemplo é simples demais, não vital - posso garantir: a maioria dos robôs que circulam no mercado (e também os comerciantes também) em suas negociações são guiados apenas pelas estatísticas de preços dos produtos que estão negociando. De qualquer forma, no problema da otimização paramétrica de uma estratégia de negociação, não há diferença fundamental entre uma negociação de robôs com base no vetor de preços e um robô que acessa uma matriz de terabytes de análises de mercado com classificação múltipla. O principal é que esses dois robôs podem (devem ser capazes de) ser testados com dados históricos. Os algoritmos devem ser determinados: ou seja, nos mesmos dados de entrada (tempo do modelo, se necessário, também podemos tomá-lo como parâmetro), o robô de negociação deve mostrar o mesmo resultado.
Mais detalhes sobre o robô de negociação podem ser encontrados no seguinte spoiler:
algoritmo de negociação com robôs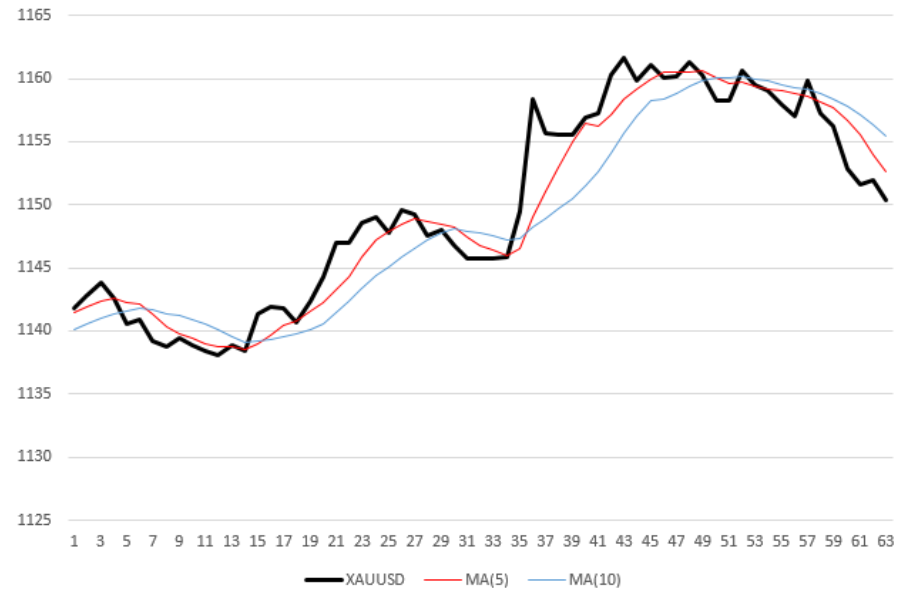
A curva preta (grossa) no gráfico é a medida de preço
XAUUSD por hora. Duas linhas finas e quebradas, vermelho e azul - valores médios de preços com períodos médios de 5 e 10, respectivamente. Em outras palavras, Média Móvel (MA) com períodos de 5, 10. Por exemplo, para calcular a ordenada do último ponto (direito) da curva vermelha, calculei a média dos últimos 5 valores de preço. Assim, cada média móvel não é apenas “suavizada” em relação à curva de preços, mas também fica pela metade do seu período em relação a ela.
Regra de Abertura de Transação
O robô possui uma regra simples para tomar uma decisão de compra / venda:
- assim que a média móvel com um período curto (
MA "rápido") cruza a média móvel com um período longo (MA "lenta") de baixo para cima, o robô compra um ativo (ouro).
Assim que o MA "rápido" cruza o MA "lento" de cima para baixo, o robô vende o ativo. Na figura acima, o robô fará 5 transações: 3 vendas nos carimbos de data / hora 7, 31 e 50 e duas compras (marcas 16 e 36).
O robô pode abrir um número ilimitado de transações. Por exemplo, em algum momento, o robô pode ter várias compras e vendas pendentes ao mesmo tempo.
Regra de fechamento da transação
O robô fecha o negócio assim que:
- o lucro da transação excede o limite especificado em porcentagem - TakeProfit,
- ou a perda na transação, em porcentagem, excede o valor correspondente - StopLoss.
Suponha que o StopLoss seja de 0,2%.
O acordo é uma "venda" de ouro ao preço de 1061,50.
Assim que o preço do ouro subir para 1061,50 + 1061,50 * 0,2% / 100% = 1063,12%, a perda do negócio será obviamente de 0,2% e o robô o fechará automaticamente.
O robô toma todas as decisões sobre abrir / fechar uma transação em pontos discretos no tempo - no final de cada hora, após a publicação da próxima cotação XAUUSD.
Sim, o robô é extremamente simples. Ao mesmo tempo, 100% atende aos requisitos:
- o algoritmo é determinístico: sempre, simulando o trabalho do robô nos mesmos dados de preço, obteremos o mesmo resultado,
- possui um número suficiente de parâmetros ajustáveis, a saber: o período de "rápido" e o período de média móvel "lenta" (números naturais), TakeProfit e StopLoss - números reais positivos,
- uma alteração em cada um dos 4 parâmetros, no caso geral, tem um efeito não linear nas características de negociação do robô, em particular na sua lucratividade,
- a lucratividade de um robô no histórico de preços é considerada um código de programa elementar e o próprio cálculo leva uma fração de segundo para um vetor de milhares de cotações,
- finalmente, o que, no entanto, é irrelevante, o robô, com toda a sua simplicidade, na realidade não será pior (embora provavelmente não seja melhor) do que o Graal vendido pelo autor na Internet por um valor imodesto.
Pesquisa rápida para um conjunto quase ideal de parâmetros de entrada
Usando o exemplo do nosso robô simples, pode-se ver que uma enumeração completa de todos os vetores possíveis das configurações do robô é muito cara, mesmo para quatro parâmetros variáveis. Uma alternativa óbvia à pesquisa exaustiva é a escolha de vetores de parâmetros para uma estratégia específica. Consideramos apenas parte de todas as combinações possíveis em busca da melhor, na qual a
FC se aproxima da mais alta (ou menor, dependendo da CF que escolhemos e que resultado alcançamos).
Consideraremos três algoritmos de busca para o valor quase
ideal do
filtro digital . Para cada algoritmo, definimos um limite de 40 testes (de 400 combinações possíveis).
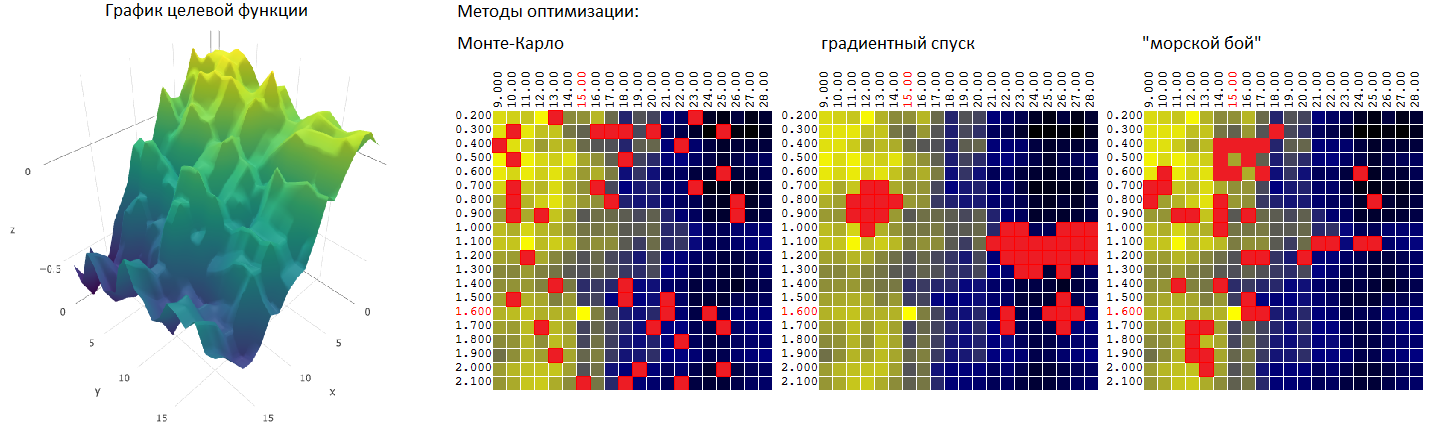
Método de Monte Carlo
ou uma seleção aleatória de M vetores não correlacionados dentre o número possível de conjuntos igual a N. O método é provavelmente o mais simples possível. Nós o usaremos como ponto de partida para comparação subsequente com outros métodos de otimização.
Exemplo 1
o gráfico mostra a dependência do lucro (P) do nosso robô comercial de negociação
EURUSD , obtido no segmento anual do histórico de medições de preço por hora, no valor do parâmetro - o período da
média móvel "lenta" (M). Todos os outros parâmetros são fixos e não são otimizados.
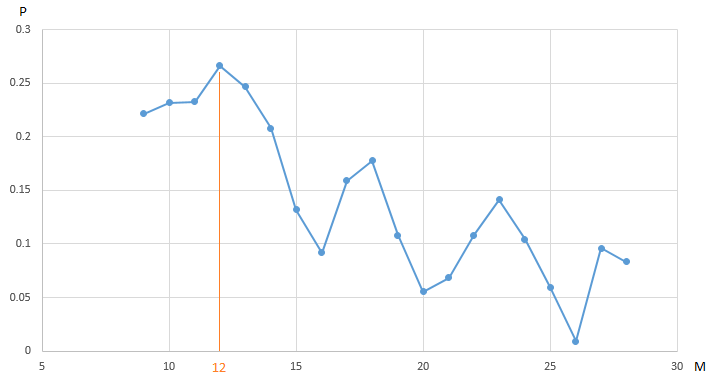
CF (lucro) atinge um máximo de 0,27 no ponto M = 12. Para garantir o valor máximo do lucro, precisamos realizar 20 iterações de teste. Uma alternativa é realizar um número menor de testes de um robô de negociação com um valor selecionado aleatoriamente do parâmetro M no intervalo [9, 20]. Por exemplo, após 5 iterações (20% do número total de testes, encontramos um vetor quase ótimo (vetor, obviamente, unidimensional) dos parâmetros: M = 18 com um valor de CF (M) igual a 0,18:

Os valores restantes no gráfico do nosso algoritmo de otimização foram ocultados pelo "nevoeiro da guerra".
A otimização de um dos quatro parâmetros do nosso robô de negociação, com valores fixos dos demais parâmetros, não nos permite ver a imagem inteira. Talvez um máximo de 0,27 CF não seja o melhor valor do indicador, se você variar o valor de outros parâmetros?

É assim que a dependência do lucro no período da média móvel muda para vários valores do parâmetro TakeProfit no intervalo [0,2 ... 0,8].
Método de Monte Carlo: otimização de dois parâmetros
A dependência do lucro de um robô de negociação em dois parâmetros pode ser representada graficamente como uma superfície:

Os dois eixos são os valores dos parâmetros T (TakeProfit) e M (período da média móvel), o terceiro eixo é o valor do lucro.
Para o nosso robô de negociação, após a realização de 400 testes em um intervalo de dados de um ano (~ 6000 cotações por hora do euro em relação ao dólar americano), obtemos uma superfície do formulário:

ou, no plano em que os valores dos ativos financeiros (lucro, P) são representados pela cor:

Escolhendo pontos arbitrários no plano, neste exemplo, o algoritmo não encontrou o valor ideal, mas se aproximou bastante dele:

Qual é a eficácia do método de Monte Carlo para encontrar a
FC máxima? Depois de realizar 1.000 iterações de pesquisa para o máximo de CF nos dados de origem do exemplo acima, obtive as seguintes estatísticas:
- o valor médio do máximo do DF encontrado durante 1.000 iterações de otimização (40 vetores aleatórios dos parâmetros [M, T] de 400 combinações possíveis) foi de 0,231 ou 95,7% do máximo global do DF (0,279).
Obviamente, ao comparar os métodos de otimização paramétrica dos robôs de negociação, uma amostra não é um indicador. Mas, por enquanto, essa avaliação é suficiente. Prosseguimos para o próximo método - o método de
descida de gradiente .
Método de descida de gradiente
Formalmente, como o nome indica, o método é usado para procurar o mínimo do DF.
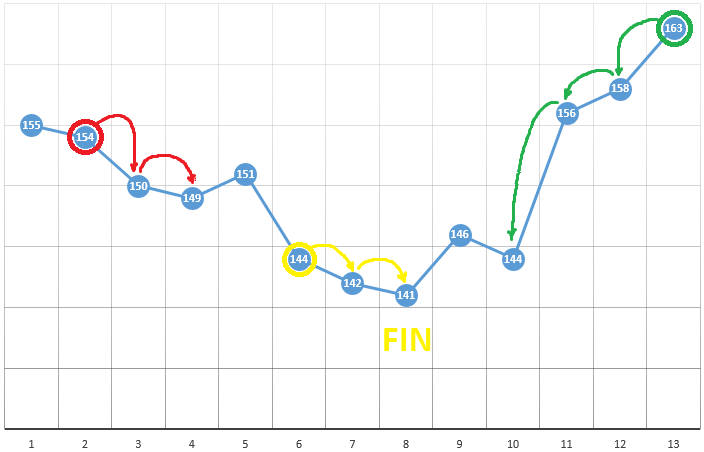
De acordo com o método, selecionamos o ponto inicial com as coordenadas [x0, y0, z0, ...]. No exemplo da otimização de um parâmetro, este pode ser um ponto selecionado aleatoriamente:
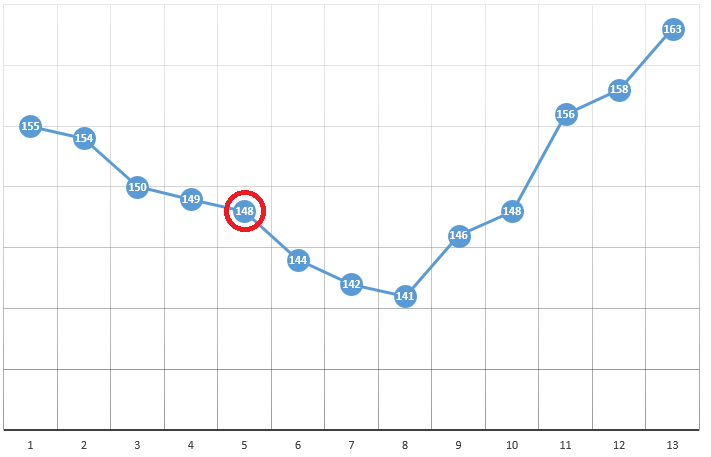
com coordenadas [5] e um valor DF de 148. A seguir, são três etapas simples:
- verifique os valores de CF nas proximidades da posição atual (149 e 144)
- mova para o ponto com o menor valor de CF
- se isso estiver ausente, um extremo local for encontrado, o algoritmo será concluído

Para otimizar o DF em função de dois parâmetros, usamos o mesmo algoritmo. Se anteriormente calculássemos a FC em dois pontos vizinhos
, agora verificamos 4 pontos:
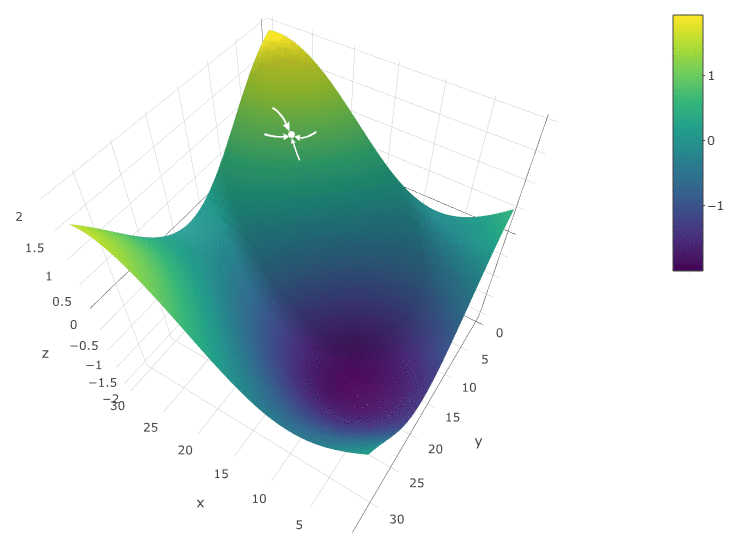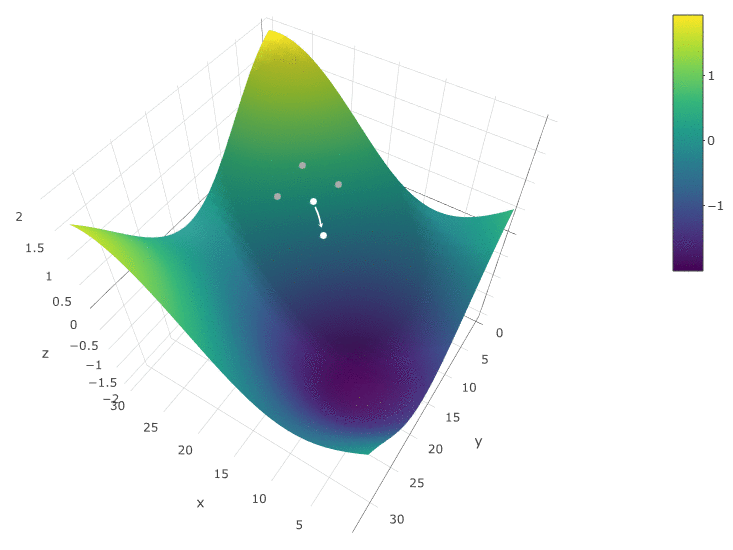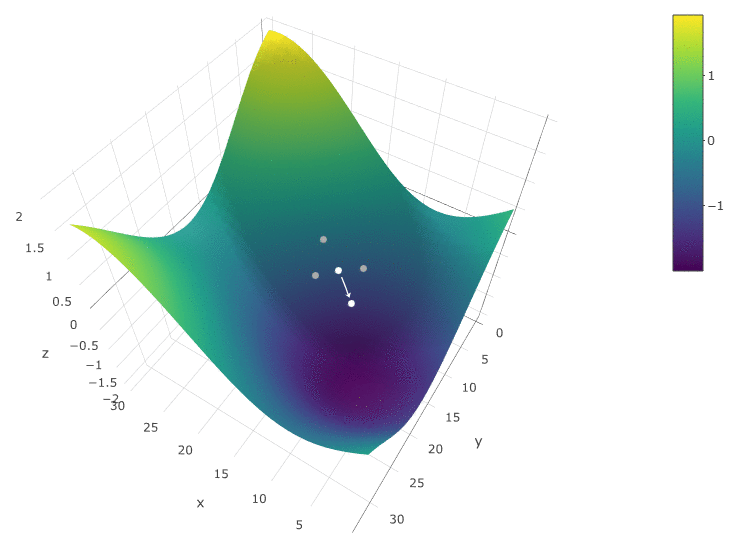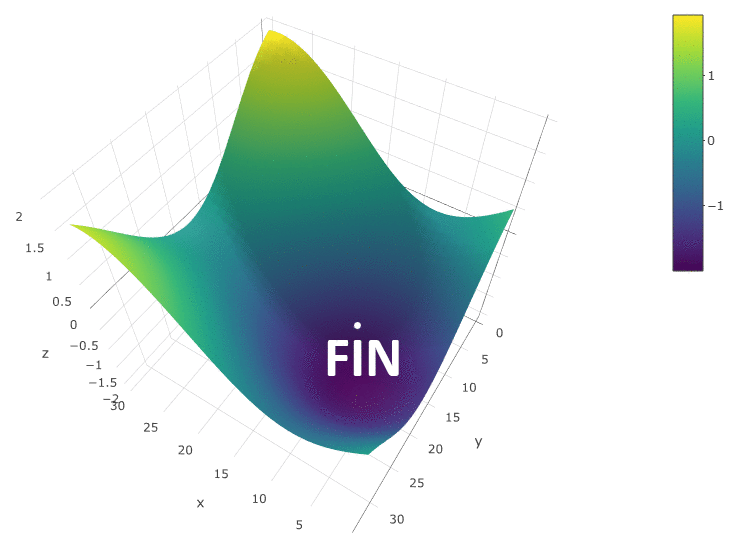
O método é definitivamente bom quando há apenas um extremo em um DF em um espaço de teste. Se houver vários extremos, a pesquisa precisará ser repetida várias vezes para aumentar a probabilidade de encontrar um extremo global:
No nosso exemplo, estamos procurando o DF
máximo . Para permanecer dentro da definição do algoritmo, podemos assumir que estamos procurando um mínimo de "menos DF". No mesmo exemplo, o lucro de um robô de negociação em função do período da média móvel e do valor TakeProfit, uma iteração:
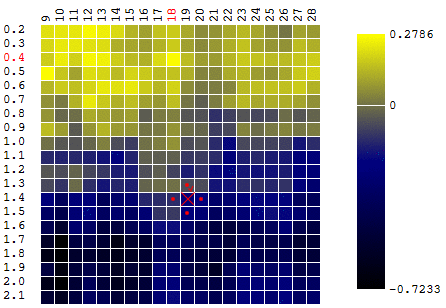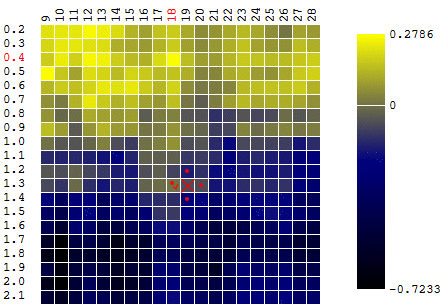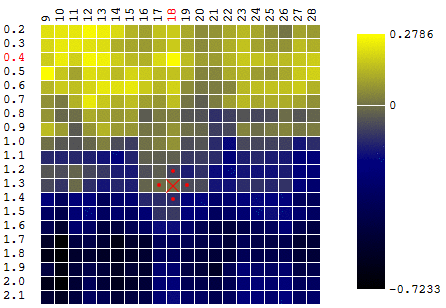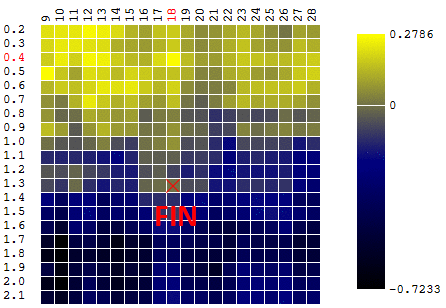
Nesse caso, foi encontrado um extremo local que está longe do máximo global da FC. Um exemplo de várias iterações da busca pelo extremo do FS pelo método de descida do gradiente, o valor do FS é calculado 40 vezes (40 pontos em 400 possíveis):

Agora, comparamos a eficiência de procurar o máximo global do CF (lucro) em nossos dados iniciais usando algoritmos de Monte Carlo e descida de gradiente. Em cada caso, são realizados 40 testes (cálculos de CF). 1.000 iterações de otimização foram realizadas por cada um dos métodos:
| Monte Carlo | descida gradiente |
|---|
| a média do valor quase ótimo obtido de FC | 0,231 | 0,200 |
| o valor obtido a partir do máximo da CF | 95,7% | 92,1% |
Como você pode ver na tabela, neste exemplo, o método de descida do gradiente é pior em sua tarefa - procurar o extremo global do ativo digital - o lucro máximo. Mas não temos pressa em descartá-lo.
Estabilidade paramétrica do algoritmo de negociação
Encontrar as coordenadas do máximo / mínimo global de um filtro digital geralmente não é uma meta de otimização. Suponha que, no gráfico, exista um pico "agudo" - um máximo global, cujo valor de CF na vizinhança seja muito menor que o valor de pico:
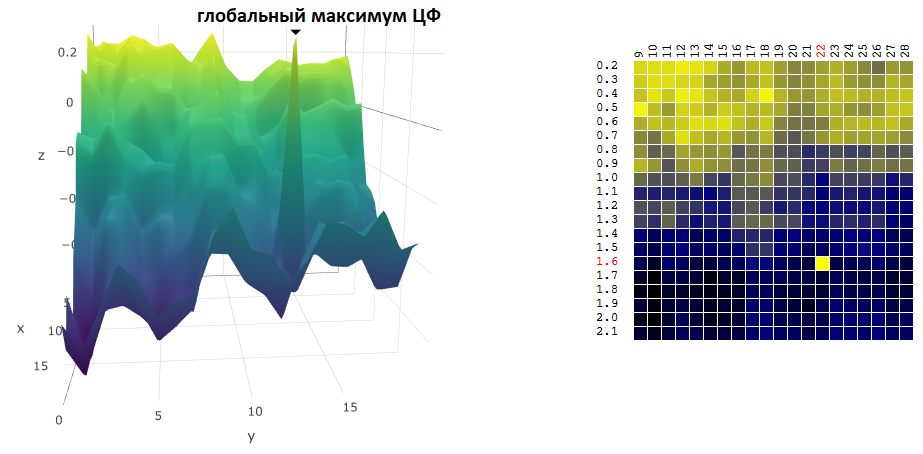
Suponha que tenhamos selecionado as configurações do robô de negociação que correspondem ao máximo encontrado do ativo digital. Se mudarmos ligeiramente o valor de pelo menos um dos parâmetros - o período da média móvel e / ou do TakeProfit - a lucratividade do robô cairá acentuadamente (se tornará negativo). Em relação à negociação real, pode-se esperar, pelo menos, que o mercado em que nosso robô negocia seja notavelmente diferente do período da história em que otimizamos o algoritmo de negociação.
Portanto, ao escolher as configurações "ideais" de um robô de negociação, vale a pena ter uma idéia de quão sensível o robô é a alterações nas configurações nas proximidades do ponto extremo encontrado do DF.
Obviamente, o método da descida do gradiente, em regra, nos fornece os valores de TF nas proximidades do extremo. O método de Monte Carlo é mais provável de acertar quadrados.
Em várias instruções para testar estratégias de negociação automatizadas, após a conclusão da otimização, é recomendável verificar os indicadores de destino do robô nas proximidades do vetor de parâmetros encontrado. Mas estes são testes adicionais. Além disso, e se a lucratividade da estratégia cair com uma ligeira mudança nas configurações? Obviamente, você deve repetir o processo de teste.
Um algoritmo seria útil para nós, o qual, ao mesmo tempo em que procurava o extremo do CF, permitiria avaliar a estabilidade da estratégia de negociação para alterar as configurações em uma faixa estreita em relação aos picos encontrados. Por exemplo, não pesquise diretamente o valor máximo de CF
e o valor médio ponderado que leva em consideração os valores vizinhos da função objetivo, em que o peso é inversamente proporcional à distância do valor vizinho (para otimizar dois parâmetros x, y e a função objetivo P):
Em outras palavras, ao escolher um vetor quase ótimo de parâmetros, o algoritmo avaliará a função objetivo "suavizada":
era tornou-se
tornou-se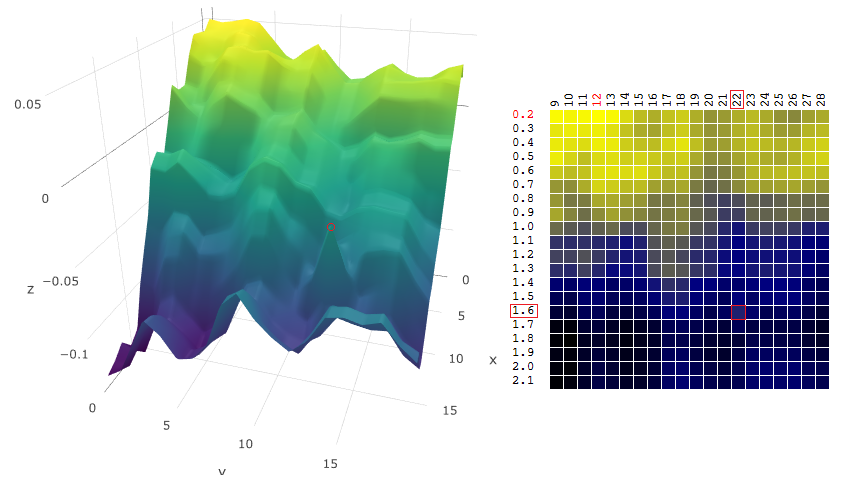
O método da "batalha marítima"
Tentando combinar as vantagens de ambos os métodos (Monte Carlo e o método de descida de gradiente), tentei um algoritmo semelhante ao algoritmo do jogo na "batalha marítima":
- primeiro, dou alguns "golpes" em toda a área
- então, em lugares de "acertos", abro fogo maciço.
Em outras palavras, os primeiros N testes são realizados em vetores aleatórios não correlacionados dos parâmetros de entrada. Destes, os melhores resultados M são selecionados. Nas proximidades desses testes (mais - minutos 0..L para cada uma das coordenadas) são realizados outros testes K.
Para o nosso exemplo (400 pontos, 40 tentativas no total), temos:
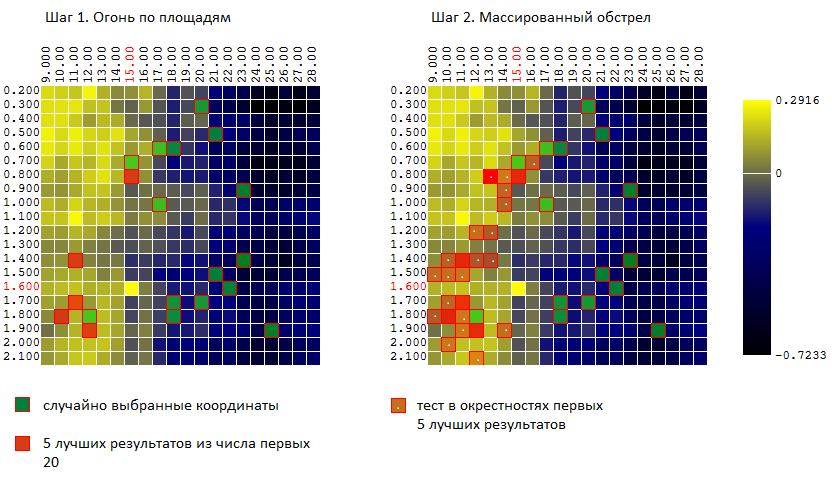
E, novamente, comparamos a eficácia dos três algoritmos de otimização agora:
| Monte Carlo | descida gradiente | "Batalha no mar" |
|---|
O valor médio do extremo encontrado da FC como uma porcentagem do valor global.
40 testes, 1.000 iterações de otimização
| 95,7% | 92,1% | 97,0% |
O resultado é encorajador. Obviamente, a comparação foi realizada em uma amostra de dados específica: um algoritmo de negociação em uma série temporal do valor do euro em relação ao dólar.
Mas, antes de comparar os algoritmos em um número maior de amostras dos dados de origem, vou falar sobre outro algoritmo popular inesperadamente (injustificável?) Para otimizar estratégias de negociação - a otimização do algoritmo genético (GA). No entanto, o artigo saiu muito volumoso e o GA terá que ser adiado para a próxima publicação .