1. Introdução

O OpenGL, que é o back-end do OpenSceneGraph, usa primitivas geométricas (como pontos, linhas, triângulos e faces poligonais) para construir todos os objetos no mundo tridimensional.

Essas primitivas são definidas por dados sobre seus vértices, que incluem as coordenadas dos vértices, componentes normais, dados de cores e coordenadas de textura. Esses dados são armazenados em matrizes especiais. As primitivas podem ser formadas, por exemplo, especificando para os objetos que os descrevem uma lista de índices de vértices. Esse método é chamado de método de matriz de vértices; elimina o armazenamento de vértices redundantes na memória e apresenta bom desempenho.

Além disso, o OpenGL pode usar o mecanismo das chamadas listas de exibição , quando as primitivas preparadas na memória de vídeo podem ser reutilizadas, o que acelera significativamente a exibição de objetos estáticos.

Por padrão, o OSG usa o método da matriz de vértices e o método da lista de exibição para renderizar a geometria. No entanto, a estratégia de renderização pode ser alterada, dependendo de como os dados geométricos são apresentados. Neste artigo, abordaremos as técnicas básicas para trabalhar com geometria no OSG.

1. Classes Geode e Drawable

A classe osg :: Geode é um terminal, o chamado nó "folha" da árvore de cenas. Ele não pode ter nós filhos, mas contém todas as informações necessárias para renderizar a geometria. Seu nome, Geode, é abreviação de nó de geometria.

Os dados geométricos a serem processados ​​pelo mecanismo são armazenados no conjunto de objetos da classe osg :: Drawable, gerenciados pela classe osg :: Geode. A classe osg :: Drawable é uma classe puramente virtual. Um número de subclasses é herdado dele, que são modelos tridimensionais, imagens e texto processados ​​pelo pipeline OpenGL. OSG refere-se a drawable como todos os elementos que podem ser desenhados pelo mecanismo.

A classe osg :: Geode fornece vários métodos para anexar e desanexar drawables:

• Método público addDrawable () - passa um ponteiro para um elemento desenhável em uma instância da classe osg :: Geode. Todos esses elementos são controlados pelos ponteiros inteligentes osg :: ref_ptr <>.
  
• O método público removeDrawable () e removeDrawables () remove o objeto de osg :: Geode e diminui a contagem de referência para ele. O método removeDrawable () usa como único parâmetro um ponteiro para o elemento de interesse, e o método removeDrawables () usa dois parâmetros: o índice inicial e o número de elementos a serem removidos da matriz de objetos osg :: Geode.
  
• O método getDrawable () retorna um ponteiro para um elemento no índice passado como parâmetro.
  
• O método getNumDrawables () retorna o número total de elementos anexados ao osg :: Geode. Por exemplo, para remover todos os elementos do osg :: Geode, você pode usar esse código
  

geode->removeDrawables(0, geode->getNumDrawables()); 

2. Desenho de formas simples

O OSG fornece a classe osg :: ShapeDrawable, que é a descendente da classe osg :: Drawable e projetada para criar primitivas tridimensionais simples. Esta classe inclui um objeto osg :: Shape que armazena informações sobre geometria específica e outros parâmetros. As primitivas são geradas usando o método setShape (), por exemplo

 shapeDrawable->setShape(new osg::Box(osg::Vec3(1.0f, 0.0f, 0.0f), 10.0f, 10.0f, 5.0f)); 

cria uma caixa retangular com um centro geométrico no ponto (1.0, 0.0, 0.0) com largura e altura de 10 e profundidade de 5 unidades. A classe osg :: Vec3 define um vetor no espaço tridimensional (além disso, as classes osg :: Vec2 e osg :: Vec4 que descrevem vetores da dimensão correspondente também são apresentadas).

As primitivas mais populares são representadas no OSG pelas classes osg :: Box, osg :: Capsule, osg :: Cone, osg :: Cylinder e osg :: Sphere.

Considere um exemplo da aplicação desse mecanismo.

main.h

 #ifndef MAIN_H #define MAIN_H #include <osg/ShapeDrawable> #include <osg/Geode> #include <osgViewer/Viewer> #endif // MAIN_H 

main.cpp

 #include "main.h" int main(int argc, char *argv[]) { (void) argc; (void) argv; osg::ref_ptr<osg::ShapeDrawable> shape1 = new osg::ShapeDrawable; shape1->setShape(new osg::Box(osg::Vec3(-3.0f, 0.0f, 0.0f), 2.0f, 2.0f, 1.0f)); osg::ref_ptr<osg::ShapeDrawable> shape2 = new osg::ShapeDrawable; shape2->setShape(new osg::Cone(osg::Vec3(0.0f, 0.0f, 0.0f), 1.0f, 1.0f)); shape2->setColor(osg::Vec4(0.0f, 1.0f, 0.0f, 1.0f)); osg::ref_ptr<osg::ShapeDrawable> shape3 = new osg::ShapeDrawable; shape3->setShape(new osg::Sphere(osg::Vec3(3.0f, 0.0f, 0.0f), 1.0f)); shape3->setColor(osg::Vec4(0.0f, 0.0f, 1.0f, 1.0f)); osg::ref_ptr<osg::Geode> root = new osg::Geode; root->addDrawable(shape1.get()); root->addDrawable(shape2.get()); root->addDrawable(shape3.get()); osgViewer::Viewer viewer; viewer.setSceneData(root.get()); return viewer.run(); } 

Este exemplo especialmente não precisa de comentários: no programa são criadas três formas simples, após a compilação e o lançamento, veremos esse resultado



O mecanismo mostrado no exemplo é simples e direto, mas não é a maneira mais eficaz de criar geometria e pode ser usado exclusivamente para testes. A classe osg :: Geometry é usada para criar geometria em aplicativos baseados em OSG de alto desempenho.

3. Armazenamento de dados de geometria: classes osg :: Array e osg :: Geometry

A classe osg :: Array é uma classe abstrata básica, da qual vários descendentes são herdados, projetados para armazenar dados que são passados ​​para as funções do OpenGL. Trabalhar com essa classe é semelhante ao trabalho com std :: vector da biblioteca padrão C ++. O código a seguir ilustra como adicionar um vetor a uma matriz de vértices usando o método push_back ()

 vertices->push_back(osg::Vec3(1.0f, 0.0f, 0.0f)); 

As matrizes OSG são alocadas na pilha e gerenciadas por ponteiros inteligentes. No entanto, isso não se aplica a elementos de matriz, como osg :: Vec3 ou osg :: Vec2, que também podem ser criados na pilha.

A classe osg :: Geometry é um invólucro sobre funções OpenGL que funcionam com matrizes de vértices. É derivado da classe osg :: Drawable e pode ser facilmente adicionado à lista de objetos osg :: Geode. Essa classe usa as matrizes descritas acima como entrada e as utiliza para gerar geometria usando o OpenGL.

4. Vértices e seus atributos

Um vértice é uma unidade atômica de primitivas de geometria. Ele possui vários atributos que descrevem um ponto no espaço bidimensional ou tridimensional. Os atributos incluem: posição, cor, vetor normal, coordenadas de textura, coordenadas de neblina e assim por diante. A parte superior deve sempre ter uma posição no espaço, pois para outros atributos, eles podem estar presentes opcionalmente. O OpenGL suporta 16 atributos básicos de vértice e pode usar matrizes diferentes para armazená-los. Todas as matrizes de atributos são suportadas pela classe osg :: Geometry e podem ser definidas usando métodos do conjunto de formulários * Array ().

Atributos de vértice no OpenSceneGraph

Atributo	Tipo de dados	Método Osg :: Geometry	Chamada equivalente ao OpenGL
Posição	3 vetores	setVertexArray ()	glVertexPointer ()
Normal	3 vetores	setNormalArray ()	glNormalPointer ()
Cor	4 vetores	setColorArray ()	glColorPointer ()
Cor secundária	4 vetores	setSecondaryColorArray ()	glSecondaryColorPointerEXT ()
Coordenadas de nevoeiro	flutuar	setFogCoordArray ()	glFogCoordPointerEXT ()
Coordenadas de textura	2 ou 3 vetores	setTexCoordArray ()	glTexCoordPointer ()
Outros atributos	Definido pelo Usuário	setVertexArribArray ()	glVertexAttribPointerARB ()

Em princípio, é necessário definir seus próprios atributos para cada um dos vértices, o que leva à formação de várias matrizes de atributos do mesmo tamanho - caso contrário, a incompatibilidade nos tamanhos das matrizes pode levar a um comportamento indefinido do mecanismo. O OSG suporta vários métodos para vincular atributos de vértice, por exemplo

 geom->setColorBinding(osg::Geometry::BIND_PER_VERTEX); 

significa que cada vértice e cada cor do vértice estão correlacionados um a um. No entanto, se você olhar para esse código

 geom->setColorBinding(osg::Geometry::BIND_OVERALL); 

então ele aplica uma cor a toda a geometria. Da mesma forma, os relacionamentos entre outros atributos podem ser configurados chamando os métodos setNormalBinding (), setSecondaryColorBinding (), setFogCoordBinding () e setVertexAttribBinding ().

5. Conjuntos de primitivas de geometria

A próxima etapa após definir as matrizes de atributos de vértice é descrever como os dados de vértice serão renderizados. A classe virtual osg :: PrimitiveSet é usada para controlar as primitivas geométricas geradas pelo renderizador a partir de um conjunto de vértices. A classe osg :: Geometry fornece vários métodos para trabalhar com conjuntos de primitivas de geometria:

• addPrimitiveSet () - passa um ponteiro para um conjunto de primitivas em um objeto osg :: Geometry.
  
• removePrimitiveSet () - remove um conjunto de primitivas. Como parâmetros, leva o índice inicial de conjuntos e o número de conjuntos a serem excluídos.
  
• getPrimitiveSet () - retorna um conjunto de primitivas no índice passado como parâmetro.
  
• getNumPrimitiveSets () - retorna o número total de conjuntos de primitivas associadas a essa geometria.
  

A classe osg :: PrimitiveSet é abstrata e não pode ser instanciada, mas várias classes derivadas que encapsulam conjuntos de primitivas com as quais o OpenGL opera, como osg :: DrawArrays e osg :: DrawElementsUInt, herdam dela.

A classe osg :: DrawArrays usa vários elementos consecutivos de uma matriz de vértices para construir uma primitiva geométrica. Ele pode ser criado e anexado à geometria chamando um método.

 geom->addPrimitiveSet(new osg::DrawArrays(mode, first, count)); 

O primeiro modo de parâmetro define o tipo primitivo para os tipos primitivos correspondentes do OpenGL: GL_POINTS, GL_LINE_STRIP, GL_LINE_LOOP, GL_LINES, GL_TRIANGLE_STRIP, GL_TRIANGLE_FAN, GL_TRIANGLES, GL_QUAD_STRIP, GL_QUADS e GL_POLY.

O primeiro e o segundo parâmetros especificam o primeiro índice na matriz de vértices e o número de vértices a partir dos quais a geometria deve ser gerada. Além disso, o OSG não verifica se o número especificado de vértices é suficiente para construir a geometria especificada pelo modo, o que pode levar à falha do aplicativo!

6. Exemplo - desenhe um quadrado pintado

Implementamos todos os itens acima como um exemplo simples


Após a compilação e execução, obtemos um resultado semelhante a este



Este exemplo precisa de esclarecimentos. Então, primeiro, criamos uma matriz de vértices do quadrado, na qual suas coordenadas são armazenadas

 osg::ref_ptr<osg::Vec3Array> vertices = new osg::Vec3Array; vertices->push_back(osg::Vec3(0.0f, 0.0f, 0.0f)); vertices->push_back(osg::Vec3(1.0f, 0.0f, 0.0f)); vertices->push_back(osg::Vec3(1.0f, 0.0f, 1.0f)); vertices->push_back(osg::Vec3(0.0f, 0.0f, 1.0f)); 

Em seguida, definimos a matriz de normais. No nosso caso simples, não precisamos criar um normal para cada vértice - apenas descreva um vetor unitário direcionado perpendicularmente ao plano do quadrado

 osg::ref_ptr<osg::Vec3Array> normals = new osg::Vec3Array; normals->push_back(osg::Vec3(0.0f, -1.0f, 0.0f)); 

Defina uma cor para cada vértice

 osg::ref_ptr<osg::Vec4Array> colors = new osg::Vec4Array; colors->push_back(osg::Vec4(1.0f, 0.0f, 0.0f, 1.0f)); colors->push_back(osg::Vec4(0.0f, 1.0f, 0.0f, 1.0f)); colors->push_back(osg::Vec4(0.0f, 0.0f, 1.0f, 1.0f)); colors->push_back(osg::Vec4(1.0f, 1.0f, 1.0f, 1.0f)); 

Agora crie um objeto de geometria onde a descrição do nosso quadrado será armazenada, que será processada pela renderização. Passamos uma matriz de vértices para essa geometria

 osg::ref_ptr<osg::Geometry> quad = new osg::Geometry; quad->setVertexArray(vertices.get()); 

Passando uma matriz de normais, informamos ao mecanismo que um único normal será usado para todos os vértices, especificando o método de ligação ("ligação") das normais BIND_OVAERALL

 quad->setNormalArray(normals.get()); quad->setNormalBinding(osg::Geometry::BIND_OVERALL); 

Passando as cores dos vértices, pelo contrário, indicamos que cada vértice terá sua própria cor

 quad->setColorArray(colors.get()); quad->setColorBinding(osg::Geometry::BIND_PER_VERTEX); 

Agora crie um conjunto de primitivas para geometria. Indicamos que as faces quadradas (GL_QUADS) devem ser geradas a partir da matriz de vértices, tomando o vértice com o índice 0 como o primeiro vértice e o número total de vértices será 4

 quad->addPrimitiveSet(new osg::DrawArrays(GL_QUADS, 0, 4)); 

Bem, acho que não vale a pena explicar a transferência de geometria e o lançamento da renderização

 osg::ref_ptr<osg::Geode> root = new osg::Geode; root->addDrawable(quad.get()); osgViewer::Viewer viewer; viewer.setSceneData(root.get()); return viewer.run(); 

O código acima é equivalente ao design a seguir no OpenGL puro

 static const GLfloat vertices[][3] = { … }; glEnableClientState( GL_VERTEX_ARRAY ); glVertexPointer( 4, GL_FLOAT, 0, vertices ); glDrawArrays( GL_QUADS, 0, 4 ); 

7. Vértices de indexação em primitivas

A classe osg :: DrawArrays funciona bem ao ler dados de vértice diretamente de matrizes, sem intervalos. No entanto, isso não é tão eficaz quando o mesmo vértice pode pertencer a várias faces de um objeto. Vejamos um exemplo.



O cubo tem oito vértices. No entanto, como pode ser visto na figura (observamos o desdobramento do cubo no avião), alguns vértices pertencem a mais de uma face. Se você construir um cubo de 12 faces triangulares, esses vértices serão repetidos e, em vez de um conjunto de 8 vértices, obteremos um conjunto de 36 vértices, a maioria dos quais na verdade é o mesmo vértice!

No OSG, existem as classes osg :: DrawElementsUInt, osg :: DrawElementsUByte e osg :: DrawElementsUShort, que usam matrizes de índice de vértice como dados para resolver o problema descrito. Matrizes de índices armazenam índices de vértices de primitivas que descrevem faces e outros elementos da geometria. Ao aplicar essas classes a um cubo, é suficiente armazenar uma matriz de oito vértices associados a faces por meio de matrizes de índices.

Classes do tipo osg :: DrawElements * são construídas da mesma maneira que a classe padrão std :: vector. Esse código pode ser usado para adicionar índices.

 osg::ref_ptr<osg::DrawElementsUInt> de = new osg::DrawElementsUInt(GL_TRIANGLES); de->push_back(0); de->push_back(1); de->push_back(2); de->push_back(3); de->push_back(0); de->push_back(2); 

Este código define a face frontal do cubo mostrado na figura.

Vamos considerar mais um exemplo ilustrativo - um octaedro



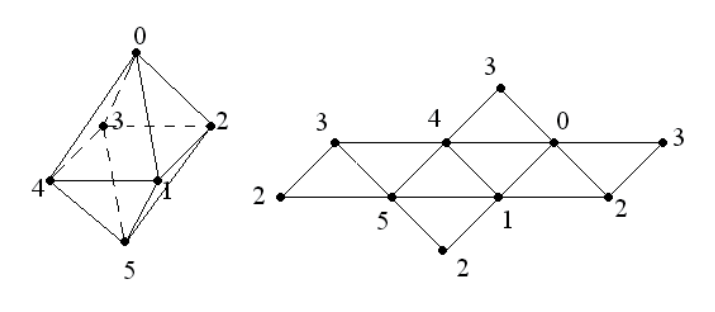
É interessante porque contém apenas seis vértices, mas cada vértice entra em até quatro faces triangulares! Podemos criar uma matriz de 24 vértices para exibir todas as oito faces usando osg :: DrawArrays. No entanto, faremos o contrário - armazenaremos os vértices em uma matriz de seis elementos e geraremos faces usando a classe osg :: DrawElementsUInt.


Vamos analisar esse código em mais detalhes. Claro, a primeira coisa que fazemos é criar uma matriz de seis vértices

 osg::ref_ptr<osg::Vec3Array> vertices = new osg::Vec3Array(6); (*vertices)[0].set( 0.0f, 0.0f, 1.0f); (*vertices)[1].set(-0.5f, -0.5f, 0.0f); (*vertices)[2].set( 0.5f, -0.5f, 0.0f); (*vertices)[3].set( 0.5f, 0.5f, 0.0f); (*vertices)[4].set(-0.5f, 0.5f, 0.0f); (*vertices)[5].set( 0.0f, 0.0f, -1.0f); 

Inicializamos cada vértice diretamente acessando o vetor de suas coordenadas usando a operação de desreferenciamento do ponteiro e operador [] (lembramos que osg :: Array é semelhante em seu dispositivo a std :: vector).

Agora crie faces como uma lista de índices de vértices

 osg::ref_ptr<osg::DrawElementsUInt> indices = new osg::DrawElementsUInt(GL_TRIANGLES, 24); (*indices)[ 0] = 0; (*indices)[ 1] = 1; (*indices)[ 2] = 2; //  0 (*indices)[ 3] = 0; (*indices)[ 4] = 4; (*indices)[ 5] = 1; //  1 (*indices)[ 6] = 4; (*indices)[ 7] = 5; (*indices)[ 8] = 1; //  2 (*indices)[ 9] = 4; (*indices)[10] = 3; (*indices)[11] = 5; //  3 (*indices)[12] = 3; (*indices)[13] = 2; (*indices)[14] = 5; //  4 (*indices)[15] = 1; (*indices)[16] = 5; (*indices)[17] = 2; //  5 (*indices)[18] = 3; (*indices)[19] = 0; (*indices)[20] = 2; //  6 (*indices)[21] = 0; (*indices)[22] = 3; (*indices)[23] = 4; //  7 

As faces serão triangulares, haverá 8, o que significa que a lista de índices deve conter 24 elementos. Os índices de faces vão sequencialmente nesta matriz: por exemplo, a face 0 é formada pelos vértices 0, 1 e 2; face 1 - vértices 0, 4 e 1; face 2 - vértices 4, 5 e 1 e assim por diante. Os vértices são listados no sentido anti-horário se você olhar para a face da face (veja a figura acima).

Etapas adicionais para criar a geometria que executamos nos exemplos anteriores. A única coisa que não fizemos foi a geração automática de normais suavizados (média), que realizamos neste exemplo chamando

 osgUtil::SmoothingVisitor::smooth(*geom); 

De fato, se os vértices de uma face são dados, é fácil calcular o normal para ela. Nos vértices em que várias faces convergem, uma certa média normal é calculada - as normais das faces convergentes são somadas e a soma resultante é normalizada novamente. Essas operações (e muito mais!) Podem ser executadas pelo próprio mecanismo usando classes da biblioteca osgUtil. Portanto, em nosso exemplo, adicionaremos uma instrução ao vinculador para criar nosso programa com esta biblioteca no arquivo * .pro

octahedron.pro

 CONFIG(debug, debug|release) { TARGET = $$join(TARGET,,,_d) . . . LIBS += -L$$OSG_LIB_DIRECTORY -losgUtild } else { . . . LIBS += -L$$OSG_LIB_DIRECTORY -losgUtil } 

Como resultado, obtemos o seguinte resultado



Para entender como isso funciona, considere o pipeline do OpenGL



O mecanismo da matriz de vértices reduz o número de chamadas do OpenGL. Ele armazena dados de vértice na memória do aplicativo, que é usada no lado do cliente. O pipeline do OpenGL no lado do servidor obtém acesso a várias matrizes de vértices. Como mostrado no diagrama, o OpenGL recebe dados do buffer de vértice no lado do cliente e, de maneira ordenada, executa a montagem de primitivas. É assim que os dados são processados ​​usando os métodos set * Array () da classe osg :: Geometry. A classe osg :: DrawArrays passa por essas matrizes diretamente e as exibe.

Ao usar osg :: DrawElements *, a dimensão das matrizes de vértices é reduzida e o número de vértices transferidos para o pipeline é reduzido. Uma matriz de índices permite criar um cache de vértices no lado do servidor. O OpenGL lê dados de vértices do cache, em vez de ler a partir do buffer de vértices no lado do cliente. Isso aumenta significativamente o desempenho geral da renderização.

8. Técnicas de processamento de malha poligonal

O OpenSceneGraph suporta várias técnicas para processar a malha poligonal de objetos de geometria de cena. Esses métodos de pré-processamento, como redução de polígono e mosaico, são frequentemente usados ​​para criar e otimizar modelos poligonais. Eles têm uma interface simples, mas, no processo, realizam muitos cálculos complexos e não são muito adequados para execução instantânea.

As técnicas descritas incluem:

1. osgUtil :: Simplifier - reduzindo o número de triângulos na geometria. O método público simplify () é usado para simplificar a geometria do modelo.
   
2. osgUtil :: SmootingVisitor - cálculo de normais. O método smooth () pode ser usado para gerar normais suavizados para o modelo, em vez de calculá-los independentemente e defini-los explicitamente por meio de uma matriz de normais.
   
3. osgUtil :: TangentSpaceGenerator - geração de vetores de base tangente para vértices do modelo. É iniciado chamando o método generate () e salva o resultado retornado pelos métodos getTangentArray (), getNormalArray () e getBinormalArray (). Esses resultados podem ser usados ​​para vários atributos de vértice ao escrever sombreadores no GLSL.
   
4. osgUtil :: Tesselator - executa mosaico de uma malha poligonal - divide primitivas complexas em uma sequência de simples (método retesselatePolygons ())
   
5. osgUtil :: TriStripVisitor - converte uma superfície geométrica em um conjunto de faixas de faces triangulares, o que permite renderizar com consumo eficiente de memória. O método stripify () converte um conjunto de primitivas de modelo em geometria com base no conjunto GL_TRIANGLE_STRIP.
   

Todos os métodos aceitam a geometria do objeto como um parâmetro passado pelo osg :: Geometry & link, por exemplo, como este

 osgUtil::TriStripVisitor tsv; tsv.stripify(*geom); 

onde geom se refere a uma instância da geometria descrita por um ponteiro inteligente.

As classes osg :: Simplifier, osg :: SmoothingVisitor e osg :: TriStripVisitor podem trabalhar diretamente com nós no gráfico de cena, por exemplo

 osgUtil::TriStripVisitor tsv; node->accept(tsv); 

O método accept () processa todos os nós filhos até que a operação especificada seja aplicada a todos os nós terminais desta parte da árvore de cenas armazenada nos nós do tipo osg :: Geode.

Vamos tentar a técnica do mosaico na prática.


Com base na posição espacial dos vértices neste exemplo, é claro que estamos tentando criar um polígono não convexo de oito vértices, usando a geração de uma face do tipo GL_POLYGON. A montagem e execução deste exemplo mostra que o resultado que esperamos não funciona - o exemplo é exibido incorretamente



Para corrigir esse problema, a geometria construída deve ser colocada em mosaico antes de passá-la ao visualizador

 osgUtil::Tessellator ts; ts.retessellatePolygons(*geom); 

após o qual obtemos o resultado correto



Como isso funciona? Um polígono não convexo, sem o uso de mosaico correto, não será exibido como esperamos, pois o OpenGL, buscando otimizar o desempenho, o considerará um polígono simples e convexo ou simplesmente o ignorará, o que pode gerar resultados completamente inesperados.

A classe osgUtil :: Tessellator usa algoritmos para transformar um polígono convexo em uma série de não-convexos - no nosso caso, transforma a geometria em GL_TRIANGLE_STRIP.



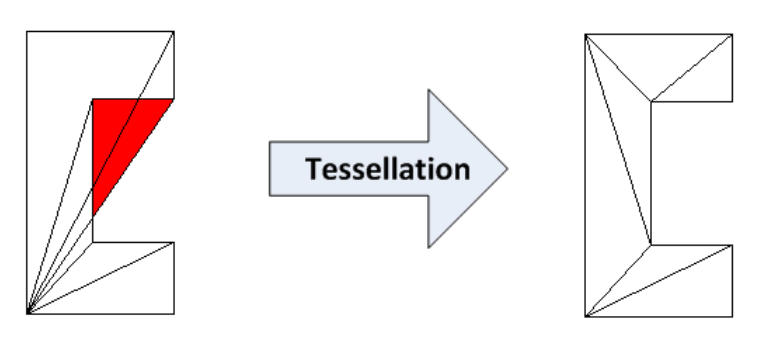
. setWindingType() , GLU_TESS_WINDING_ODD GLU_TESS_WINDING_NONZERO, .

Conclusão

Neste artigo, obtivemos um entendimento básico de como a geometria de objetos tridimensionais é armazenada e processada no mecanismo OSG. Não pense que os exemplos simples e não muito impressionantes considerados no artigo são o limite das capacidades do mecanismo. Apenas esses exemplos podem ajudar o desenvolvedor a entender a mecânica do OpenSceneGraph e, sem esse entendimento, é difícil imaginar o trabalho de coisas mais complexas.

Este artigo é baseado na tradução e processamento do texto dos capítulos correspondentes do livro OpenSceneGraph 3.0. Guia do Iniciante . Todos os exemplos são verificados por mim pessoalmente, e seu código fonte está disponível aqui . Para continuar ...