Há várias tarefas nas quais um sinal de longa data é dividido em segmentos, cada um dos quais é processado separadamente. Em particular, essa abordagem é usada para analisar o sinal usando a janela Fourier transform, ou vice-versa, na síntese; bem como no processamento espectral, como remoção de ruído, mudança de andamento, filtragem não linear, compactação de dados de áudio e outros.

O processo de particionamento é representado matematicamente pela multiplicação por alguma função de peso ( janela ) com um deslocamento. Para a janela mais simples - retangular - pode ser assim:

Sinal de origem:



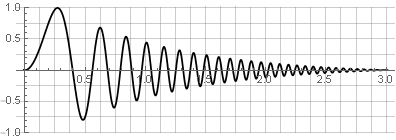
Partições:







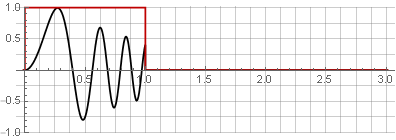
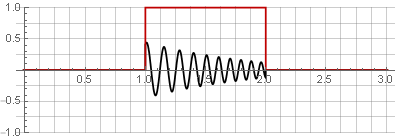
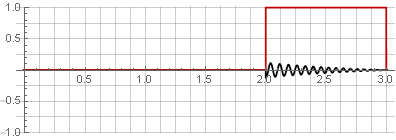
Você pode restaurar o sinal original simplesmente adicionando-o.

Mais detalhes

No entanto, por Por várias razões, uma função retangular não é a melhor função da janela. Na análise espectral, através da transformada de Fourier discreta (geralmente rápida) discreta, o bloco de dados analisados ​​parece “girar”, o que leva a uma lacuna nas bordas e à distorção do espectro:



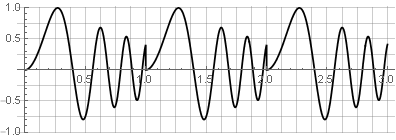
Também não é adequado para síntese reversa - já que qualquer alteração também levará a quebras - por exemplo, se tentarmos reverter uma das partes:



Para eliminar esses inconvenientes, a sobreposição é usada - quando cada janela subseqüente captura parte dos dados da anterior; e a janela de peso, respectivamente, cai gradualmente nas bordas.

Sobreposição a 50%

Na maioria das vezes, eles usam a janela Hannah (também conhecida como "cosseno elevado") com uma sobreposição de 50%:








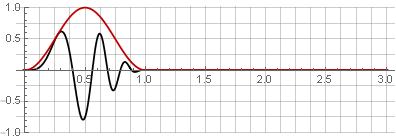
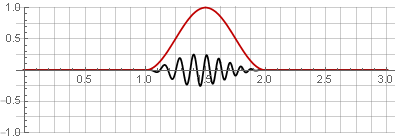
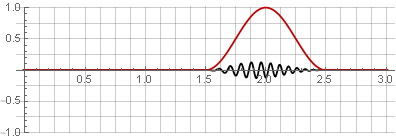
Devido à simetria da função cosseno durante a adição, eles são somados à unidade:



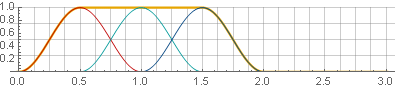
Agora, com a síntese inversa, não teremos lacunas - mas apenas na condição de que nas bordas da janela os valores ainda cheguem a zero. Por exemplo, ao reverter uma das partes, a suavidade não será violada:

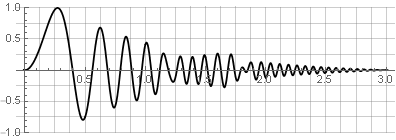
Processamento de sobreposição dupla

Considere com mais detalhes o algoritmo para processar um sinal usando a transformada rápida de Fourier (FFT):

1. dividir o sinal em segmentos com uma sobreposição de janela;
2. FFT direta;
3. processamento espectro;
4. FFT inversa;
5. sobreposição de janela repetida (porque após a FFT reversa, as bordas não serão necessariamente zeradas sem quebrar);
6. somatória dos segmentos resultantes.

Além disso, se o processamento do espectro não for realizado, o sinal de saída deve ser idêntico ao sinal de entrada (apenas com um atraso de tempo inevitável).

Ao usar a janela Hann, a sobreposição de 50% não é mais suficiente, pois ocorrerão quedas:



Como a sobreposição dupla equivale a quadrado, a solução óbvia seria usar a raiz da janela Hann para compensar o quadrado:



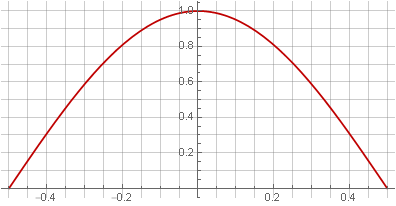
Nesse caso, no entanto, a janela deixou de ser suave nas bordas - uma lacuna apareceu na primeira derivada.


Você pode seguir o outro caminho - use a sobreposição de 75% e as janelas também serão somadas em uma constante - apenas não em $$$1$e em $$$\ frac {3} {2}$:



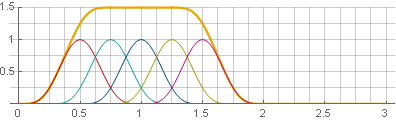
Nesse caso, tivemos apenas sorte. Se expandirmos o quadrado na soma, podemos ver que é uma composição de duas janelas Hannah, mas em escalas diferentes, o que nos permite atender aos requisitos de que precisamos:

$$

$$\ left (\ frac {\ cos (2 \ pi x) +1} {2} \ right) ^ 2 = \ frac {\ cos (2 \ pi x) +1} {2} + \ frac {\ cos (4 \ pi x) -1} {8}$$

Com outras funções da janela, esse truque não funcionará; Além disso, nem todas as funções padrão da janela podem fornecer somas em uma constante, mesmo com sobreposição de 50%.

Idéia

Podemos considerar a janela Hann não como uma função independente, mas como a diferença entre duas funções contínuas por partes (um artigo separado foi dedicado a uma discussão detalhada sobre elas) com um deslocamento. Por exemplo, usando a seguinte função

$$

$$\ left \ {\ begin {array} {ll} -1 & x \ leqslant -1 \\ 1 & x \ geqslant 1 \\ \ sin \ left (\ frac {\ pi x} {2} \ right) & -1 <x <1 \\ \ end {array} \ right.$$

pode escrever

$$

$$f (x + 1) -f (x-1)$$

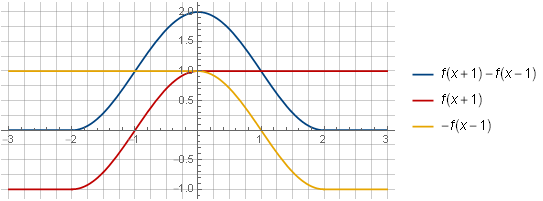
Tendo considerado os componentes da soma de duas dessas janelas, sua capacidade de resumir em uma constante se tornará mais visual:



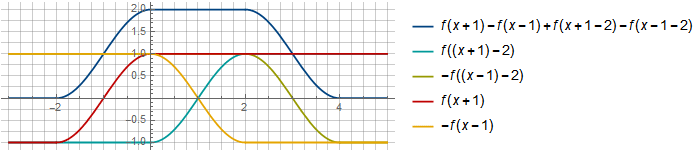
No segmento $$$[0,2]$recebemos compensação mútua além de funções $$$-f (x-1)$e $$$f ((x + 1) -2)$desde $$$f ((x + 1) -2) = f (x-1)$

Você pode escolher outro deslocamento, com mais sobreposições, por exemplo:

$$

$$f \ left (x + \ frac {1} {2} \ right) -f \ left (x- \ frac {1} {2} \ right)$$

E então, ao mudar de etapa $$$\ frac {1} {2}$, eles também serão somados em uma constante:



Pode-se observar que, se você reorganizar os componentes da função de janela, obtém as mesmas janelas Hann.

Assim, usando diferentes funções de restrição, é possível formar janelas com a forma requerida.

Fórmula final

Agora, resta apenas definir a escala para que as áreas e valores de definição não dependam da quantidade de sobreposição. Definindo uma janela em um intervalo $$$[0,1]$nós temos

$$

$$\ frac {f \ left (\ frac {2 tx} {t-1} -1 \ right) -f \ left (\ frac {2 t (x-1)} {t-1} +1 \ right) } {2}$$

onde $$$f$- função contínua por partes do formulário

$$

$$\ left \ {\ begin {array} {ll} -1 & x \ leqslant -1 \\ 1 & x \ geqslant 1 \\ g (x) & -1 <x <1 \\ \ end {array} \ certo.$$

mas $$$g$- alguma função de interpolação entre pontos $$$(- 1, -1)$e $$$(1,1)$.

Parâmetro $$$t$determina o nível de sobreposição - um divisor que determina a etapa pela qual cada próxima janela deve ser deslocada, $$$x_ {n + 1} = x_n + \ frac {1} {t}$e deve ser maior que um, $$$t> 1$.

Porcentagem de sobreposição $$$p$pode ser calculado pela fórmula

$$

$$p = \ frac {100 (t-1)} {t}$$

e vice-versa

$$

$$t = \ frac {100} {100-p}$$

A aparência final da janela dependerá da escolha do nível de sobreposição e da escolha da função limitadora.

Alguns exemplos interessantes

Aqui veremos algumas soluções prontas, para as quais tudo foi iniciado. Para simplificar, consideramos uma função simplesmente interpoladora $$$g (x)$, sem qualquer outra fita.

Janelas polinomiais

Eles são os menos computacionalmente caros. Usando a fórmula derivada anteriormente

$$

$$\ frac {2 x \ Gamma \ left (n + \ frac {1} {2} \ right) \, _2F_1 \ left (\ frac {1} {2}, 1-n; \ frac {3} {2} ; x ^ 2 \ right)} {\ sqrt {\ pi} \ Gama (n)}$$

obtemos um polinômio com um número determinado de zeros em derivadas mais altas que fornecem a suavidade necessária da janela nas bordas.


Com uma sobreposição de 75% da janela com valores diferentes de n, as janelas ficarão assim:



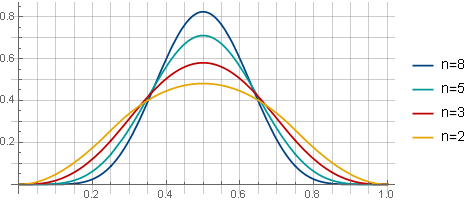
E no caso de extração de raiz - assim (ao usar 75% de sobreposição):



mais ou menos (ao usar sobreposição de 50%):

A janela mais suave

Função

$$

$$\ tanh \ left (\ frac {k x} {\ sqrt {1-x ^ 2}} \ right)$$

É interessante que seja infinitamente diferenciável e todas as suas derivadas nas bordas sejam 0 (o que pode ser comprovado considerando-se suas derivadas com base em regras de diferenciação - em cada termo, haverá um fator de zero). Isso nos permite construir janelas com base em todos os derivados, sem lacunas:

Vista da janela "saia"

A necessidade desse tipo de janela é causada pelo aumento da resolução da FFT, mas pela redução do efeito do efeito “incerteza de tempo e frequência” em altas frequências, aumentando sua concentração no centro.

Primeiro, determinamos o tipo desejado de função da janela - por exemplo, da seguinte maneira:

$$

$$- \ log \ left (k ^ 2 x ^ 2 + 1 \ right) + \ log \ left (k ^ 2 + 1 \ right) - \ frac {k ^ 2 \ left (1-x ^ 2 \ right) } {k ^ 2 + 1}$$

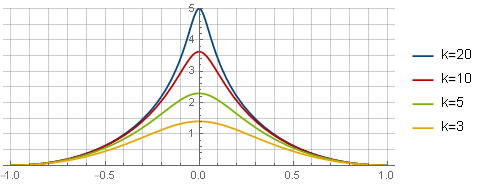
Aqui, o primeiro termo determina a forma da função em si, o segundo - fornece a interseção com o eixo da abcissa, o terceiro (parábola) redefine a derivada nas bordas para um encaixe suave; e o parâmetro $$$k$define a "nitidez" do pico. Neste formulário, ele ainda não é adequado para uso - primeiro você precisa obter a função de restrição através da integração e dimensionamento:

$$

$$\ frac {kx \ esquerda (k ^ 2 \ esquerda (x ^ 2 + 3 \ direita) +6 \ direita) +3 \ esquerda (k ^ 2 + 1 \ direita) \ esquerda (kx \ esquerda (\ log \ left (k ^ 2 + 1 \ right) - \ log \ left (k ^ 2 x ^ 2 + 1 \ right) \ right) -2 \ tan ^ {- 1} (kx) \ right)} {4 k ^ 3-6 \ esquerda (k ^ 2 + 1 \ direita) \ tan ^ {- 1} (k) +6 k}$$

Por conveniência, você pode vincular o parâmetro $$$k$ao nível de sobreposição $$$t$- por exemplo, para que a quarta derivada no centro da janela seja 0 - e depois $$$k$será considerado como $$$\ sqrt {3} (t-1)$:



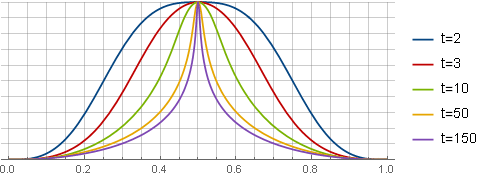
Aqui, para maior clareza, todas as janelas são reduzidas na mesma escala.

Janela de visualização da agulha

É uma versão mais "agressiva" da janela anterior. Foi escolhida uma hipérbole como base, a partir da qual, através de sucessivas transformações

$$

$$\ frac {1} {x} \ to \ frac {1} {\ sqrt {x ^ 2}} \ to \ frac {1} {\ sqrt {x ^ 2 + 1}} \ para \ frac {1} {\ sqrt {k ^ 2 x ^ 2 + 1}} \ to \ frac {\ left (1-x ^ 2 \ right) ^ 2} {\ sqrt {k ^ 2 x ^ 2 + 1}}$$

e usando as mesmas etapas na forma de integração e dimensionamento obteve a fórmula

$$

$$\ frac {kx \ esquerda (2 k ^ 2 \ esquerda (x ^ 2-4 \ direita) -3 \ direita) \ sqrt {k ^ 2 x ^ 2 + 1} + \ esquerda (8 \ esquerda (k ^ 4 + k ^ 2 \ direita) +3 \ direita) \ sinh ^ {- 1} (kx)} {\ left (8 \ left (k ^ 4 + k ^ 2 \ right) +3 \ right) \ sinh ^ {-1} (k) -3 k \ sqrt {k ^ 2 + 1} \ esquerda (2 k ^ 2 + 1 \ direita)}$$

Aqui você também pode vincular o parâmetro $$$k$ao nível de sobreposição. A solução direta da equação da 4ª derivada fornece um resultado complicado, então faça a imagem da janela anterior na imagem e semelhança definindo $$$k$como $$$k (t-1)$garantindo assim o papel do parâmetro $$$k$como "ajuste fino". At $$$k = 2,22$O Windows ficará assim:

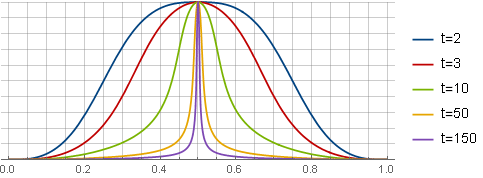
Janela assimétrica

A função da janela não precisa ser simétrica. Digamos que precisamos de uma janela com um ataque agudo e atenuação suave. Podemos obtê-lo de acordo com um esquema já familiar - primeiro determine a forma desejada da função e, em seguida, pela integração, obtemos a função de restrição. Aqui a tarefa é um pouco mais complicada devido ao fato de que, devido à assimetria, o centro não passa mais pela origem, portanto, uma etapa de cálculo adicional é adicionada. Isso também leva ao fato de que as fórmulas, como resultado, são bastante complicadas. Por exemplo, considere a opção mais simples - uma parábola multiplicada por uma janela de peso polinomial:

$$

$$(1-x) ^ 2 \ esquerda (1-x ^ {10} \ direita) ^ 2$$

Aqui, o grau de x na janela ponderada (ou seja, 10) determina a "nitidez" do ataque. Usamos um valor específico, em vez de um parâmetro simbólico, para simplificar as fórmulas para maior clareza - se desejar, você pode recalculá-lo mais tarde.

Após a integração, o simples dimensionamento não é mais suficiente - você ainda precisa alinhar as bordas:



Para fazer isso, primeiro deslocamos a função para cima para alinhar a borda esquerda e depois a escalamos para as duas na borda direita e subtraímos uma. Então obtemos a seguinte fórmula:

$$

$$\ frac {8775 \ left (\ frac {x ^ {27}} {27} - \ frac {2 x ^ {26}} {26} + \ frac {x ^ {25}} {25} - \ frac {2 x ^ {15}} {15} + \ frac {4 x ^ {14}} {14} - \ frac {2 x ^ {13}} {13} + \ frac {x ^ 3} {3} -x ^ 2 + x + \ frac {117592} {61425} \ right)} {9856} -1$$

Para que a janela final tenha a aparência desejada, também é necessário fornecer um nível suficientemente grande de sobreposição:

Conclusão

Da mesma forma, você pode construir janelas a partir de qualquer outra função em forma de sino - por exemplo, Gaussians; e você também pode modificar os que já foram considerados para proporcionar maior suavidade ou alterar a forma da curva.

Fora de consideração, a composição espectral de tais funções de janela permaneceu - estudos separados devem ser dedicados a isso.

Uma versão ligeiramente mais avançada do artigo (com a capacidade de alterar dinamicamente os parâmetros nas janelas sob consideração e fórmulas ocultas) na forma de um documento do Wolfram Mathematica pode ser baixada aqui .