🎂 🤜🏿 😢 Quantos programadores você precisa para suportar códigos escritos anteriormente? ✍🏿 👨‍👦 🙂

Algum tempo atrás, ocorreu uma conversa entre mim e meu bom amigo, na qual as seguintes frases soaram:

- O número de programadores crescerá constantemente - porque a quantidade de código está aumentando e cada vez mais desenvolvedores são constantemente necessários para suportá-lo.
- Mas o código está envelhecendo, parte dele está deixando o suporte. A presença de algum tipo de equilíbrio não é descartada.

Lembrando-os alguns dias depois, imaginei se o suporte ao código, exigindo mais e mais recursos ao longo do tempo, poderia paralisar o desenvolvimento de novas funcionalidades ou exigiria um aumento ilimitado no número de programadores? A análise matemática e as equações diferenciais ajudaram a avaliar qualitativamente a dependência do volume de suporte no desenvolvimento e a encontrar respostas para as perguntas.

A primeira pergunta Pode apoiar "comer" todos os recursos de desenvolvimento?

Considere uma equipe de programadores em que o número de participantes seja constante. Parte do seu tempo de trabalho

m u (t)

$\ mu (t)$ (

0 < m u (t) < 1

$0 <\ mu (t) <1$ ) recai sobre o desenvolvimento de um novo código e a fração restante do tempo

1 - m u (t)

$1- \ mu (t)$ vai apoiar. Sob as premissas do modelo, suponha que o primeiro tipo de atividade tenha como objetivo aumentar a quantidade de código e o segundo - altere-o (corrigindo erros) e não afete significativamente a quantidade de código.

Nós denotamos

y (t)

$y (t)$ todo o código escrito por hora

t

$t$ . Considerando que a velocidade de escrever código é proporcional

m u (t)

$\ mu (t)$ nós obtemos:

f r a c d y (t) d t = a_{0} m u (t); a_{0} i n m a t h b b R, a_{0} > 0.

$\ frac {dy (t)} {dt} = a_0 \ mu (t); a_0 \ in \ mathbb {R}, a_0> 0.$

É natural supor que o trabalho envolvido na manutenção do código seja proporcional ao seu volume:

1 - m u (t) = a_{1} y (t); a_{1} i n m a t h b b R, a_{1} > 0

$1- \ mu (t) = a_1 y (t); a_1 \ in \ mathbb {R}, a_1> 0$

m u (t) = 1 - a_{1} a (t)

$\ mu (t) = 1-a_1a (t)$

De onde

f r a c d y (t) d t = a_{0} (1 - a_{1} y (t))) .

$\ frac {dy (t)} {dt} = a_0 (1-a_1y (t))).$

Temos uma equação diferencial que se integra facilmente. Se, no momento inicial, a quantidade de código for zero, então

y (t) = f r a c 1 a_{1} (1 - e^{- a_{0} a_{1} t}) .

$y (t) = \ frac {1} {a_1} (1-e ^ {- a_0a_1t}).$

t a + i n f t y

$t \ a + \ infty$ função

y (t) t o 1 / a_{1}

$y (t) \ to1 / a_1$ e

m u (t) a 0

$\ mu (t) \ a 0$ . E isso significa uma redução gradual ao longo do tempo do desenvolvimento de novas funcionalidades para zero e da transição de todos os recursos para suporte.

No entanto, se a tempo

h > 0

$h> 0$ Como o código se torna obsoleto e deixa de ser suportado, a quantidade de código que requer suporte por vez

t

$t$ igual a

y (t) - y (t - h) .

$y (t) - y (t-h).$ Então

1 - m u (t) = a_{1} (y (t) - y (t - h)),

$1- \ mu (t) = a_1 (y (t) - y (t-h)),$

m u (t) = 1 - a_{1} (y (t) - y (t - h)),

$\ mu (t) = 1-a_1 (y (t) - y (t-h)),$

mas

y (t)

$y (t)$ é uma solução de uma equação diferencial com um argumento atrasado [1]:

f r a c d y (t) d t = a_{0} (1 - a_{1} (y (t) - y (t - h))) .

$\ frac {dy (t)} {dt} = a_0 (1-a_1 (y (t) - y (t-h))).$

A solução para esta equação é determinada exclusivamente pela configuração dos valores

y (t)

$y (t)$ "Antes do início dos tempos", com

t e m [- h, 0]

$t \ em [-h, 0]$ . Como nenhum código foi escrito antes da hora inicial, no nosso caso

y (t) = 0

$y (t) = 0$ às

t e m [- h, 0]

$t \ em [-h, 0]$ .

Vejamos alguns exemplos. Mediremos o tempo em anos e a quantidade de código em milhares de linhas. Então para

a_{0}

$a_0$ Valores da ordem de dezenas são aceitáveis, tomamos 50 e 100. Ou seja, em um ano a equipe de desenvolvimento escreverá cinquenta e cem mil linhas de código, respectivamente. Para

a_{1}

$a_1$ valores aceitáveis podem ser:

$inline$ ,

1 / a_{0}

$1 / a_0$ . Isso significa que a equipe de desenvolvimento é capaz de manter a quantidade de código que ele escreveu para o ano, com um quarto, metade ou carga de trabalho completa. Como o tempo médio de vida do código, vamos definir os valores: 1, 2 e 4 anos. Resolvendo a equação numericamente, obtemos exemplos do comportamento da função

m u (t)

$\ mu (t)$ para algumas combinações de parâmetros

h, a_{0}, a_{1}

$h, a_0, a_1$ .
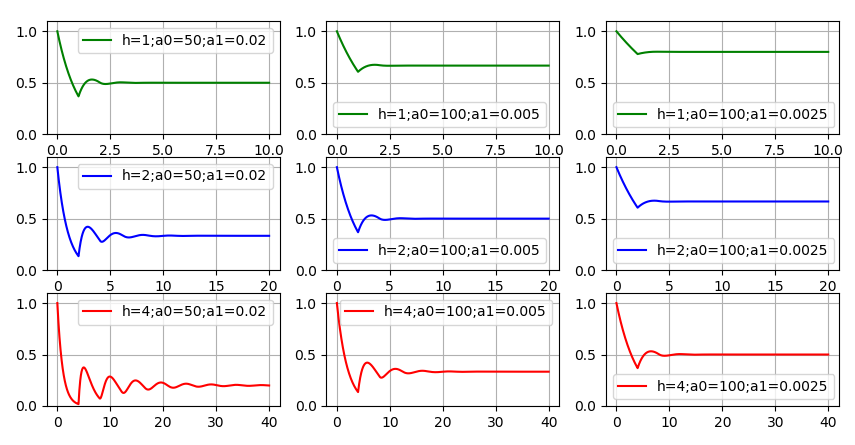
imagem

Função Comportamento

m u (t)

$\ mu (t)$ em face do código antigo mudou. A função deixou de ser monótona, mas as flutuações “se acalmam” ao longo do tempo, há uma tendência a

m u (t)

$\ mu (t)$ para algum valor constante. Os gráficos mostram: quanto mais

h

$h$ ,

a_{0}

$a_0$ e

a_{1}

$a_1$ isto é, quanto mais lento o código envelhece, mais rápido ocorre o desenvolvimento de um novo código e menor a qualidade do código, menos recursos permanecerão para o desenvolvimento de novas funcionalidades. Havia um desejo de dar pelo menos um exemplo em que

m u (t)

$\ mu (t)$ "Snuggled" perto de zero. Mas isso exigiu a seleção de indicadores de qualidade de desenvolvimento muito ruins e código de longa duração. Mesmo no gráfico inferior esquerdo, resta uma quantidade significativa de recursos para a nova funcionalidade. Portanto, a resposta correta para a primeira pergunta é mais provável: teoricamente - sim, é possível; praticamente - dificilmente.

Perguntas que não puderam ser respondidas:

É verdade que $\ mu (t)$ tende a um certo limite para $t \ a + \ infty$ para todos $a_0, a_1> 0$ ? Se não for para todos, então para qual?
Se o limite existir, como seu valor depende de $a_0, a_1$ ?

A segunda pergunta. O suporte ao código pode causar crescimento ilimitado no número de programadores?

Nós denotamos

q (t)

$q (t)$ número de programadores envolvidos no desenvolvimento de novo código. Como acima

y (t)

$y (t)$ - a quantidade de código escrito pela hora

t

$t$ . Então

f r a c d y (t) d t = a_{2} q (t); a_{2} i n m a t h b b R, a_{2} > 0.

$\ frac {dy (t)} {dt} = a_2 q (t); a_2 \ in \ mathbb {R}, a_2> 0.$

Deixe o código suportar ocupado

p (t)

$p (t)$ programadores. Envelhecimento do código C

p (t) = a_{3} (y (t) - y (t - h)); a_{3} i n m a t h b b R, a_{3} > 0.

$p (t) = a_3 (y (t) -y (t-h)); a_3 \ in \ mathbb {R}, a_3> 0.$

De onde

p (t) = a_{3} i n t_{t - h}^{t} f r a c d y (s) d s d s = a_{2} a_{3} i n t_{t - h}^{t} q (s) d s .

$p (t) = a_3 \ int_ {t-h} ^ {t} \ frac {dy (s)} {ds} ds = a_2a_3 \ int_ {t-h} ^ tq (s) ds.$

q (t) l e q C_{1}

$q (t) \ leq C_1$ então

p (t) l e q a_{1} a_{2} C_{1} h .

$p (t) \ leq a_1a_2C_1h.$

Portanto, a resposta para a segunda pergunta é negativa: se o número de desenvolvedores de novo código for limitado, no contexto do código antigo, o suporte não poderá causar um aumento ilimitado no número de programadores.

Conclusão

Os modelos considerados são modelos matemáticos "suaves" [2]. Eles são muito simples. No entanto, a dependência dos resultados da simulação sobre os valores dos parâmetros corresponde ao esperado para sistemas reais, o que favorece a adequação dos modelos e a precisão suficiente para obter estimativas qualitativas.

Referências

1. Elsgolts L.E., Norkin S.B. Introdução à teoria das equações diferenciais com argumento divergente. Moscovo Editora "Ciência". 1971
2. Arnold V.I. Modelos matemáticos "rígidos" e "flexíveis". Moscovo Editora do Centro. 2004.

Quantos programadores você precisa para suportar códigos escritos anteriormente?

A primeira pergunta Pode apoiar "comer" todos os recursos de desenvolvimento?

A segunda pergunta. O suporte ao código pode causar crescimento ilimitado no número de programadores?

Conclusão

Referências

More articles: