O novo modelo estatístico parece minar as premissas há muito aceitas da teoria dos números. Quanto você pode confiar nela, se apenas evidências rigorosas realmente importam?
Recentemente, quatro pesquisadores criaram um modelo que inverte todo o senso comum de seu campo de pesquisa. Eles usaram dados computacionais para sugerir que a visão predominante de várias décadas de um dos conceitos fundamentais era errônea.
E estes não são biólogos, climatologistas ou físicos. Em seu campo científico, os modelos empíricos não têm voz a dizer em relação à verdade. São matemáticos, representantes da disciplina, cuja moeda padrão - uma prova lógica inegável - geralmente os salva de debates que afetam outras áreas. E, no entanto, aqui estão elas, com seu modelo dizendo que provavelmente é hora de revisar algumas das idéias de longa data.
Um modelo
publicado on-line em 2016 e pronto para aparecer no Journal of the European Mathematics Society pertence a um conceito matemático tão venerável como a classificação de uma equação algébrica. Rank é uma medida correspondente a quantas soluções da equação se relacionam com números racionais e quais são irracionais. Equações de alto escalão têm soluções mais racionais e são mais complicadas.
Desde o início do século XX, os matemáticos têm se interessado pela questão de saber se existem restrições na altura da classificação da equação. A princípio, quase todo mundo achou que a restrição deveria existir. Mas na década de 1970, a opinião predominante havia mudado - a maioria dos matemáticos começou a acreditar que a classificação era ilimitada, o que significa que é possível detectar curvas com fileiras infinitamente grandes. Foi o que aconteceu, embora alguns matemáticos acreditassem que não havia argumentos fortes para apoiar essa opinião.
“As pessoas são muito autoritárias sobre a ausência de restrições. No entanto, quando você começa a entender, as evidências são extremamente fracas ”, disse
Andrew Granville , matemático da Universidade de Montreal e da University College London.
Hoje, as evidências sugerem o contrário. Dois anos após o surgimento do modelo, ela convenceu muitos matemáticos de que a classificação das equações algébricas de um determinado tipo era realmente limitada. No entanto, nem todo mundo pensa que este modelo é convincente. A falta de concordância levanta questões que nem sempre estão relacionadas a resultados matemáticos - qual o peso que as evidências empíricas podem ter em uma área em que apenas provas rigorosas são importantes?
"Não há justificativa matemática de que esse modelo seja exatamente o que precisamos", disse
Jennifer Park , matemática da Universidade de Ohio, coautora do trabalho. "Além disso, do ponto de vista experimental, muitas coisas funcionam."
Ponto a ponto
Se você receber uma equação, poderá desenhar uma curva de suas soluções no gráfico. Os matemáticos querem saber quantas dessas soluções são racionais - elas pertencem ao tipo de números, que pode ser expresso como a razão de dois números inteiros (1/2, -3 ou 4483/929).
É difícil encontrar soluções racionais de forma sistemática, mas os matemáticos têm técnicas que funcionam sob certas condições. Tome a equação x
2 + y
2 = 1. O gráfico de soluções para esta equação é um círculo. Para encontrar todos os pontos racionais do círculo, começamos com uma solução definida - digamos, a partir do ponto em que x = 1 e y = 0. Em seguida, desenhe uma linha nesse ponto que cruza o círculo em outro ponto. Se a inclinação da nossa linha é racional, o segundo ponto de interseção também será uma solução racional. Ao traçar uma linha, aumentamos o número de decisões racionais de um para dois.
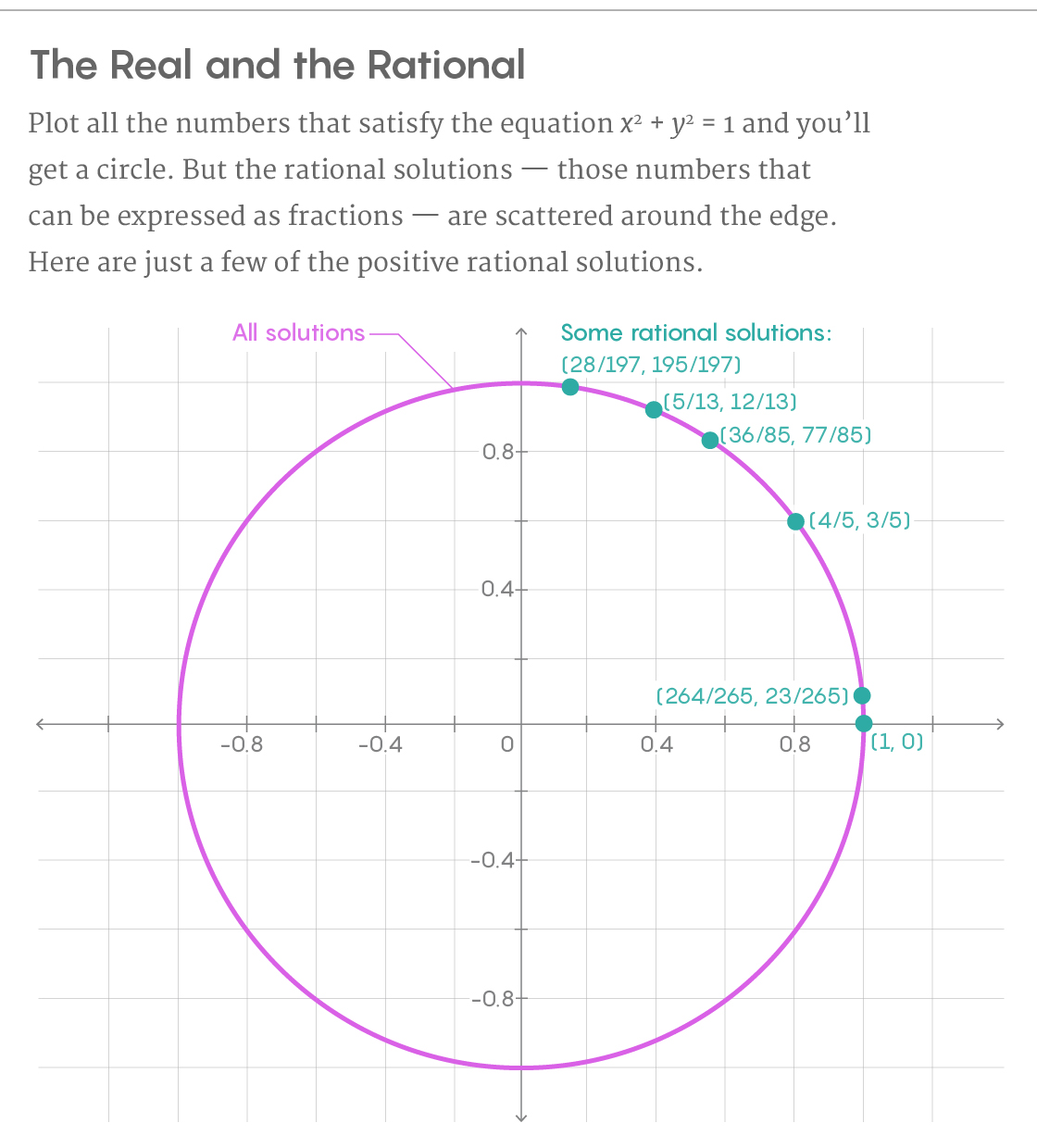
E não há necessidade de parar por aí. Repetimos o procedimento traçando uma linha reta com outra inclinação racional através do segundo ponto racional - ele cruza o círculo no terceiro ponto racional. Continuando esse caminho até o infinito, encontraremos todos os pontos racionais do círculo, dos quais existe um número infinito.
E, no caso de um círculo, você precisa começar de apenas um ponto e pode encontrá-los todos. O número de decisões racionais que você precisa conhecer no início para encontrar todas as outras é conhecido como o ranking da curva. A classificação é uma maneira elegante de descrever um conjunto infinito de decisões racionais em um único número. "É a melhor maneira de descrever as soluções racionais para essas curvas", disse
Bjorn Puunen , matemático do MIT, co-autor do modelo, com Park,
John Voight, do Dartmouth College, e
Melanie Matchet Wood, da Universidade de Wisconsin.
Um círculo é uma equação quadrática, ou uma equação de segundo grau ("grau" significa a magnitude do maior dos graus dos termos da equação). Por mais de cem anos, os matemáticos sabem como encontrar soluções racionais para as equações do segundo grau.
O próximo tipo de equações são as curvas elípticas, nas quais existem variáveis elevadas ao terceiro grau. As curvas elípticas existem no campo mais atraente da pesquisa matemática. Como são mais complicadas do que as equações de segunda ordem, são interessantes para estudar, mas não são muito complicadas. O procedimento alterado para desenhar linhas retas ainda é aplicável às curvas elípticas, mas deixa de funcionar com equações de quarta ordem e superiores.
As curvas elípticas vêm em diferentes categorias. Com algumas curvas elípticas, você pode começar de um ponto racional, aplicar o procedimento de desenhar linhas e não encontrar todas as soluções racionais. Pode ser necessário adicionar um segundo ponto racional que não esteja relacionado ao primeiro. Com isso, você iniciará um novo procedimento para desenhar linhas e encontrará um equilíbrio de pontos racionais. Uma curva, para encontrar todos os pontos racionais dos quais você precisa conhecer dois pontos racionais inicialmente, tem uma classificação igual a dois.
Não há restrição comprovada na altura da classificação de uma curva elíptica. Quanto maior a classificação da equação, mais amplo e mais complexo é o conjunto de soluções racionais da curva. "O ranking de alguma forma mede a complexidade do conjunto de decisões", disse Puunen.
No entanto, a classificação escapa às tentativas dos matemáticos para descrevê-lo em teoria. Se você receber uma curva elíptica, ela não terá uma relação óbvia entre a aparência e a classificação. "Se eu tenho uma curva elíptica e ajusto os coeficientes um pouco, então sua classificação muda radicalmente", disse Park. - Você pode alterar o coeficiente por um, e a classificação aumentará para um milhão. Ninguém sabe como se comportam as fileiras.
A falta de uma teoria geral levou os matemáticos a recuar para o pequeno conjunto de evidências que eles têm para especular sobre a existência de uma restrição na classificação. "O ponto de vista é que não há restrições na classificação, porque as pessoas o tempo todo encontraram cada vez mais altos escalões", disse Granville. O atual recordista é uma curva elíptica do ranking 28, descoberta em 2006 por Noam Elkis, matemático da Universidade de Harvard.
Mas então esse novo modelo apareceu e afirmou que era quase certamente o fim do caminho.
Surpresa em torno de 21
Para estudar fenômenos que são muito complexos ou inacessíveis para pesquisa direta, os cientistas usam modelos. Depois de criarem um análogo de um buraco negro em laboratório, eles podem aprender algo sobre como os buracos negros reais se comportam, sem precisar caminhar ao longo do horizonte de eventos.
Os matemáticos fazem o mesmo. Um bom exemplo é o estudo de números primos. Os matemáticos querem saber a resposta para a pergunta sobre
números primos gêmeos - existe um número infinito de pares de números primos que diferem em 2 (3 e 5, 11 e 13). Uma resposta exaustiva vai além do conhecimento deles, mas eles criaram modelos que prevêem a frequência de números gêmeos - e a resposta parece ser que eles ocorrem um número infinito de vezes.
O novo modelo não estuda diretamente as curvas elípticas. Ela explora um objeto matemático como
o núcleo da matriz . Núcleos se referem a curvas elípticas, como ratos para pessoas não são a mesma coisa, mas são mais fáceis de estudar, e podemos esperar que estejam perto o suficiente para tirar conclusões sobre alguns com base em experimentos em outros. Em particular, os kernels têm sua própria versão de
classificação . Tendo estudado a distribuição da classificação dos núcleos - quantos núcleos têm uma classificação de 1, quantos núcleos têm uma classificação de 2 e assim por diante - quatro matemáticos esperavam ter uma idéia da distribuição das classificações das curvas elípticas. De fato, eles apostam que a distribuição das fileiras dos núcleos e das curvas elípticas são semelhantes entre si.
 Jennifer Park, Bjorn Puunen e Melanie Wood
Jennifer Park, Bjorn Puunen e Melanie Wood"O salto de fé entra em jogo", disse Park. "Esperamos que talvez exista outro conjunto de objetos matemáticos que seja muito mais compreensível e tenha a mesma distribuição de classificação que as curvas elípticas".
Quando os quatro pesquisadores fizeram esse trabalho, a maioria dos matemáticos considerou a classificação ilimitada. No entanto, o modelo contou uma história diferente. Ela diz que existe apenas um número finito de curvas elípticas com uma classificação superior a 21. E se houver um número finito delas, uma delas terá a classificação mais alta - o que significa que a classificação ainda tem um limite superior. Quando os quatro matemáticos viram isso, perceberam que tinham um resultado vivo em suas mãos.
"Essa previsão não corresponde ao que todos acreditavam, pelo menos ao que eles admitiam publicamente", disse Wood. "Ninguém acreditava que as fileiras poderiam ter uma limitação."
Se a fé no modelo requer um passo bastante sério, então, quando o modelo relata que o senso comum estava errado, é necessário um passo ainda maior. No entanto, muitas evidências falam em favor desse resultado. Este modelo é baseado em modelos anteriores criados por outros matemáticos que estudaram várias propriedades das curvas elípticas. Esses modelos resistiram ao teste do tempo; algumas dessas previsões foram comprovadas.
"Ninguém sugeriu começar do zero e criar um novo modelo", disse Wood. "A questão era como enriquecer os modelos existentes nos quais as pessoas já acreditam".
Outro motivo para acreditar no modelo foi que um valor de classificação 21 não parece ser um limite arbitrário. Dez anos antes, Granville criou outro modelo, a partir do qual também se seguiu que deveria haver apenas um número limitado de curvas elípticas com uma classificação superior a 21. O modelo de Granville não se parecia com o atual - e o fato de ambos atribuírem o ranking 21 como significativo era muito diferente de uma simples coincidência do ponto de vista de muitos matemáticos.
"Temos dois modelos heurísticos completamente diferentes e ambos deram o mesmo número, 21 - surpreendeu as pessoas", disse Park.
Talvez a razão mais convincente de que o modelo pareça credível seja o fato de suas outras previsões corresponderem quase exatamente às propriedades comprovadas das curvas elípticas. A conclusão generalizada do modelo - a existência de um número finito de curvas elípticas com uma classificação superior a 21 - aplica-se a todas as curvas elípticas. No entanto, eles têm certas famílias, para muitas das quais matemáticos já determinaram os limites das fileiras. O modelo também previu valores de classificação para muitas dessas famílias, e suas previsões foram semelhantes, ou mesmo coincidiram exatamente com os limites que os matemáticos já determinaram.
"Nossas fronteiras previram com precisão todos os casos que foram estudados por outras pessoas", disse Park. "As pessoas são céticas em relação aos meus relatórios, mas quando menciono outras coincidências, elas ficam muito surpresas com isso."
Entre Evidência e Evidência
O modelo tem muito apoio, mas nem todo mundo acredita, e pode ser que esteja errado. O cético mais importante é Noam Elkis, um matemático de Harvard que estabeleceu um recorde para uma curva elíptica. Nas décadas desde que ele se tornou o professor mais jovem em Harvard, ele recebeu vários resultados indicando a ausência de um limite de classificação. "Minha opinião não mudou por muito tempo - não acho que estejamos bem versados nesta edição para apoiar essa ou aquela hipótese", escreveu-me Elkis por correio.
Elkis acredita que o modelo pode não funcionar corretamente de várias maneiras. Ele leva em consideração as curvas selecionadas aleatoriamente ou, em certo sentido, as curvas são médias. No entanto, existem evidências, incluindo pesquisas do próprio Elkis, sobre a possibilidade da existência de famílias de curvas elípticas, cada uma das quais inclui um número infinito dessas curvas, cujo comportamento difere significativamente do comportamento das curvas típicas. “Modelos heurísticos baseados no comportamento esperado de curvas aleatórias podem não contar toda a história sobre comportamento extremo”, escreve Elkis.
Mesmo um dos autores do modelo não está completamente certo disso. "Eu diria que sou limitado em fileiras como um agnóstico", disse Wood. Ela admite que o modelo pode estar incorreto por razões expressas por Elkis. Mas se o modelo não lidar com a tarefa, porque não levou em consideração algumas propriedades ocultas e inesperadas das curvas elípticas. "A questão é: se você não acredita em fileiras limitadas, em que lugar o modelo para de funcionar?" - disse Wood.
“Provavelmente, eles estarão certos se alguém não apresentar algum motivo engenhoso para estar errado. Não tenho ideia se existe ou não esse motivo ”, disse Alexander Smith, um estudante de Harvard que trabalha com Elkis e estuda as fileiras das curvas elípticas.
Os autores do modelo não elevam sua importância ao dogma. Eles sabem a diferença entre evidência e evidência e entendem que nenhuma montanha da primeira leva à segunda. Mas eles acreditam que seu trabalho, no mínimo, fornece uma base razoável para reflexão sobre conceitos matemáticos básicos após um século de raciocínio simples.
"Talvez encontrar curvas elípticas de ordem superior seja um desafio para os matemáticos", disse Park. Ou, talvez, os matemáticos "devam reconsiderar sua opinião sobre o que acreditamos, como uma hipótese popular".