Olá andarilhos. Nós, como viajantes em nossos pensamentos, e analisadores de nossa condição, devemos entender onde é bom e onde, onde exatamente, onde estamos, e quero chamar a atenção dos leitores para isso.
Como reunimos cadeias de pensamentos, sequencialmente?, Assumindo a conclusão de cada passo, controlando o fluxo de controle e o estado das células na memória? Ou simplesmente descrevendo a declaração do problema, diga ao programa qual tarefa específica você deseja resolver, e isso é suficiente para gravar todos os programas. Não transforme a codificação em um fluxo de comandos que alterará o estado interno do sistema, mas expresse o princípio como o conceito de classificação, porque você não precisa imaginar que tipo de algoritmo está oculto lá, basta obter os dados classificados. Não é à toa que o presidente da América pode mencionar a bolha, ele expressa a ideia de que ele entendeu algo na programação. Ele acabou de descobrir que existe um algoritmo de classificação, e os dados na tabela em sua área de trabalho, por si mesmos, não podem se alinhar, de alguma maneira mágica, em ordem alfabética.
Essa ideia de que estou bem disposta em relação à maneira declarativa de expressar pensamentos e de expressar tudo com uma sequência de comandos e transições entre eles parece arcaica e desatualizada, porque nossos avós fizeram isso, avós ligaram os contatos no painel de remendo e as luzes piscavam, e temos um monitor e reconhecimento de voz, pois nesse nível de evolução você ainda pode pensar em seguir os comandos ... Parece-me que se você expressar o programa em uma linguagem lógica, ele parecerá mais compreensível, e isso pode ser feito em tecnologia, uma aposta foi feita nos anos 80.
Bem, a introdução se arrastou ....
Para começar, tentarei recontar o mecanismo de classificação rápida. Para classificar uma lista, você precisa dividi-la em duas sub-listas e combinar a sub-lista classificada com outra sub-lista classificada .
A operação de divisão deve poder transformar a lista em duas sublistas, uma delas contém todos os elementos menos básicos e a segunda lista contém apenas elementos grandes. Expressando isso, apenas duas linhas são escritas em Erlang:
qsort([])->[]; qsort([H|T])->qsort([X||X<-T,X<H])++[H|qsort([X||X<-T,X>=H])].
Essas expressões do resultado do processo de pensamento são de interesse para mim.
É mais difícil fornecer uma descrição do princípio de classificação de forma imperativa. Como poderia haver uma vantagem nesse método de programação e, então, você não o chama, mesmo que exista um lugar-lugar, pelo menos um fortran. É porque o javascript e todas as tendências das funções lambda nos novos padrões de todas as línguas são uma confirmação do inconveniente da algorítmicaidade.
Tentarei realizar um experimento para verificar as vantagens de uma abordagem e de outra, para testá-las. Vou tentar mostrar que o registro declarativo da definição de classificação e seu registro algorítmico podem ser comparados em termos de desempenho e concluir como formular os programas mais corretamente. Talvez isso leve a programação à prateleira por meio de algoritmos e fluxos de comando, como abordagens simplesmente desatualizadas que não são relevantes, porque não é menos moderno expressá-la em um Haskell ou em uma seção transversal. E talvez não apenas a fidelidade possa dar aos programas uma aparência clara e compacta?
Usarei o Python para demonstração, uma vez que possui vários paradigmas, e isso não é C ++ e não é mais citado. Você pode escrever um programa claro em um paradigma diferente:
Classificar 1
def qsort(S): if S==[]:return [] H,T=S[0],S[1:] return qsort([X for X in T if X<T])+[H]+qsort([X for X in T if X>=T])
As palavras podem ser ditas da seguinte maneira: a classificação leva o primeiro elemento como base e, em seguida, todos os menores são classificados e conectados a todos os maiores, antes da classificação .
Ou talvez essa expressão funcione mais rápido do que a classificação escrita na forma desajeitada de uma permutação de alguns elementos próximos ou não. É possível expressar isso de forma mais sucinta e não exigir tantas palavras para isso. Tente formular em voz alta o princípio da classificação por bolha e diga ao presidente dos Estados Unidos , porque ele recebeu esses dados sagrados, ele aprendeu sobre os algoritmos e colocou-os, por exemplo, assim: Para classificar a lista, é necessário pegar alguns elementos, compará-los e se o primeiro for maior que o segundo, eles deverão ser trocados, reorganizados e, então, você deverá repetir a pesquisa de pares desses elementos desde o início da lista até que as permutações terminem .
Sim, o princípio de classificar uma bolha soa ainda mais longo que a versão de classificação rápida, mas a segunda vantagem não é apenas na brevidade do registro, mas também em sua velocidade, a expressão da mesma classificação rápida formulada pelo algoritmo será mais rápida do que a versão declarada expressamente? Talvez precisemos mudar nossos pontos de vista sobre o ensino de programação, é necessário como os japoneses tentaram introduzir o ensino do prólogo e o pensamento relacionado nas escolas. Você pode se mover sistematicamente para a distância das linguagens algorítmicas de expressão dos pensamentos.
Classificar 2
Para reproduzir isso, tive que recorrer à literatura , esta é uma declaração de Hoar , tento transformá-la em Python:
def quicksort(A, lo, hi): if lo < hi: p = partition(A, lo, hi) quicksort(A, lo, p - 1) quicksort(A, p + 1, hi) return A def partition(A, lo, hi): pivot = A[lo] i = lo - 1 j = hi + 1 while True do: i= i + 1 while A[i] < pivot do : j= j - 1 while A[j] > pivot if i >= j: return j A[i],A[j]=A[j],A[i]
Admiro o pensamento, um ciclo interminável é necessário aqui, ele teria inserido um ir-lá)), havia alguns brincalhões.
Análise
Agora vamos fazer uma lista longa e classificá-la pelos dois métodos, e entender como expressar nossos pensamentos de maneira mais rápida e eficiente. Qual abordagem é mais fácil de seguir?
Criando uma lista de números aleatórios como um problema separado, é assim que pode ser expresso:
def qsort(S): if S==[]:return [] H,T=S[0],S[1:] return qsort([X for X in T if X<H])+[H]+qsort([X for X in T if X>=H]) import random def test(len): list=[random.randint(-100, 100) for r in range(0,len)] from time import monotonic start = monotonic() slist=qsort(list) print('qsort='+str(monotonic() - start))
Aqui estão as medidas obtidas:
>>> test(10000) qsort=0.046999999998661224 >>> test(10000) qsort=0.0629999999946449 >>> test(10000) qsort=0.046999999998661224 >>> test(100000) qsort=4.0789999999979045 >>> test(100000) qsort=3.6560000000026776 >>> test(100000) qsort=3.7340000000040163 >>>
Agora repito isso na formulação do algoritmo:
def quicksort(A, lo, hi): if lo < hi: p = partition(A, lo, hi) quicksort(A, lo, p ) quicksort(A, p + 1, hi) return A def partition(A, lo, hi): pivot = A[lo] i = lo-1 j = hi+1 while True: while True: i=i+1 if(A[i]>=pivot) or (i>=hi): break while True: j=j-1 if(A[j]<=pivot) or (j<=lo): break if i >= j: return max(j,lo) A[i],A[j]=A[j],A[i] import random def test(len): list=[random.randint(-100, 100) for r in range(0,len)] from time import monotonic start = monotonic() slist=quicksort(list,0,len-1) print('quicksort='+str(monotonic() - start))
Eu tive que trabalhar para transformar o exemplo original do algoritmo de fontes antigas para a Wikipedia. Então isto: você precisa pegar o elemento de suporte e organizar os elementos no subarray para que tudo fique cada vez menos à esquerda e mais e mais à direita. Para fazer isso, troque a esquerda pelo elemento direito. Repetimos isso para cada sub-lista do elemento de referência dividido pelo índice; se não houver nada para alterar, terminamos .
Total
Vamos ver qual será a diferença horária para a mesma lista, que é classificada por dois métodos por vez. Realizaremos 100 experimentos e construiremos um gráfico:
import random def test(len): t1,t2=[],[] for n in range(1,100): list=[random.randint(-100, 100) for r in range(0,len)] list2=list[:] from time import monotonic start = monotonic() slist=qsort(list) t1+=[monotonic() - start]
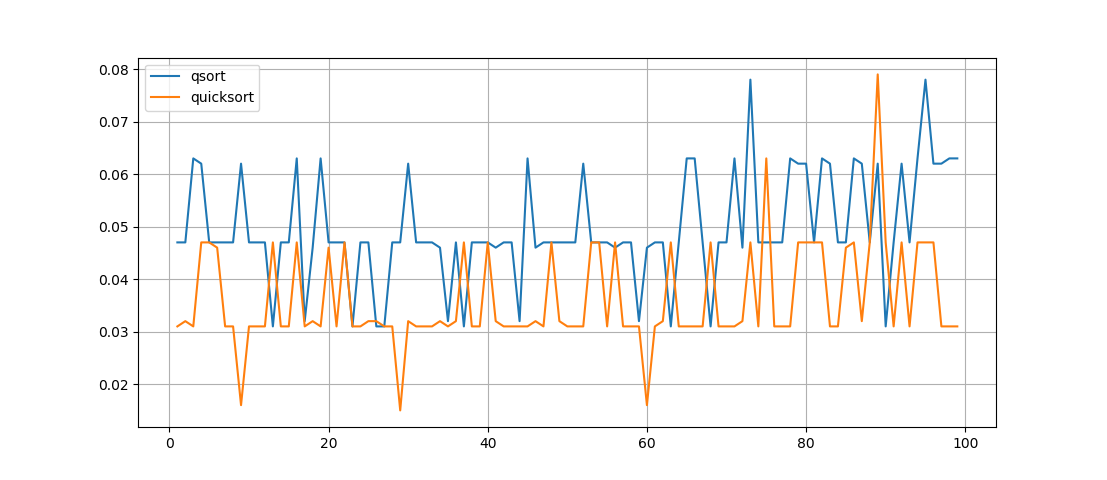
O que pode ser visto aqui - a função quicksort () funciona mais rápido , mas seu registro não é tão óbvio, embora a função seja recursiva, mas não é nada fácil entender o trabalho das permutações realizadas nela.
Bem, que expressão do pensamento de classificação é mais consciente?
Com uma pequena diferença no desempenho, obtemos uma grande diferença no volume e na complexidade do código.
Talvez a verdade seja suficiente para aprender idiomas imperativos, mas o que é mais atraente para você?
PS. E aqui está o prólogo:
qsort([],[]). qsort([H|T],Res):- findall(X,(member(X,T),X<H),L1), findall(X,(member(X,T),X>=H),L2), qsort(L1,S1), qsort(L2,S2), append(S1,[H|S2],Res).