SDRAM DDR3 moderno. Fonte: BY-SA / 4.0 by KjerishDurante uma recente visita ao
Museu da História do Computador em Mountain View, uma amostra antiga de
memória de
ferrite chamou minha atenção.
Fonte: BY-SA / 3.0 de Konstantin LanzetCheguei rapidamente à conclusão de que não tenho ideia de como essas coisas funcionam. Os anéis giram (não) e por que três fios passam por cada anel (ainda não entendo como eles funcionam). Mais importante, percebi que tenho muito pouca ideia de como funciona a moderna RAM dinâmica!
Fonte: Ciclo de Memória de Ulrich DrapperEu estava particularmente interessado em uma das consequências de como a RAM dinâmica funciona. Acontece que cada bit de dados é armazenado por uma carga (ou sua ausência) em um pequeno capacitor no chip de RAM. Mas esses capacitores perdem gradualmente sua carga ao longo do tempo. Para evitar a perda de dados armazenados, eles devem ser atualizados regularmente para restaurar a cobrança (se houver) ao seu nível original. Esse
processo de atualização envolve a leitura de cada bit e a gravação novamente. Durante esta "atualização", a memória está ocupada e não pode executar operações normais, como gravar ou armazenar bits.
Isso me incomodou por um longo tempo, e eu me perguntava ... é possível notar um atraso na atualização no nível do programa?
Base de treinamento de atualização dinâmica de RAM
Cada DIMM consiste em "células" e "linhas", "colunas", "lados" e / ou "fileiras".
Esta apresentação da Universidade de Utah explica a nomenclatura. A configuração da memória do computador pode ser verificada com o
decode-dimms . Aqui está um exemplo:
$ decode-dimms
Tamanho 4096 MB
Bancos x Linhas x Colunas x Bits 8 x 15 x 10 x 64
Fileiras 2
Não precisamos entender todo o esquema DDR DIMM, queremos entender a operação de apenas uma célula que armazena um pouco de informação. Mais precisamente, estamos interessados apenas no processo de atualização.
Considere duas fontes:
Cada bit na memória dinâmica deve ser atualizado: isso geralmente acontece a cada 64 ms (a chamada atualização estática). Esta é uma operação bastante cara. Para evitar uma grande parada a cada 64 ms, o processo é dividido em 8192 operações de atualização menores. Em cada um deles, o controlador de memória do computador envia comandos de atualização para os chips DRAM. Após receber as instruções, o chip atualizará 1/8192 células. Se você contar, então 64 ms / 8192 = 7812,5 ns ou 7,81 μs. Isso significa o seguinte:
- Um comando de atualização é executado a cada 7812,5 ns. É chamado tREFI.
- O processo de atualização e recuperação leva algum tempo, para que o chip possa executar novamente operações normais de leitura e gravação. O chamado tRFC é igual a 75 ns ou 120 ns (como na documentação da Micron mencionada).
Se a memória estiver quente (acima de 85 ° C), o tempo de armazenamento de dados na memória diminuirá e o tempo de atualização estática será reduzido pela metade para 32 ms. Consequentemente, o tREFI cai para 3906,25 ns.
Um chip de memória típico está ocupado atualizando por uma parte significativa de sua vida: de 0,4% a 5%. Além disso, os chips de memória são responsáveis pelo compartilhamento não trivial do consumo de energia de um computador típico, e a maior parte desse poder é gasta em atualizações.
O chip de memória inteiro está bloqueado durante a atualização. Ou seja, cada bit na memória é bloqueado por mais de 75 ns a cada 7812 ns. Vamos medir.
Preparação da experiência
Para medir operações com precisão de nanossegundos, você precisa de um ciclo muito apertado, talvez em C. Parece o seguinte:
for (i = 0; i < ...; i++) {
O código completo está disponível no GitHub.O código é muito simples. Execute a leitura da memória. Despejamos dados do cache da CPU. Nós medimos o tempo.
(Nota: no
segundo experimento, tentei usar o MOVNTDQA para carregar dados, mas isso requer uma página de memória especial não armazenável em cache e direitos de root).
No meu computador, o programa exibe os seguintes dados:
# timestamp, tempo de ciclo
3101895733, 134
3101895865, 132
3101896002, 137
3101896134, 132
3101896268, 134
3101896403, 135
3101896762, 359
3101896901, 139
3101897038, 137
Geralmente, é obtido um ciclo com uma duração de cerca de 140 ns, periodicamente o tempo salta para cerca de 360 ns. Às vezes, resultados estranhos aparecem acima de 3200 ns.
Infelizmente, os dados são muito barulhentos. É muito difícil verificar se há um atraso perceptível associado aos ciclos de atualização.
Transformação rápida de Fourier
Em algum momento, ocorreu-me. Como queremos encontrar um evento com um intervalo fixo, podemos enviar dados para o algoritmo FFT (transformação rápida de Fourier), que descriptografa as principais frequências.
Não sou o primeiro a pensar sobre isso: Mark Seaborn com a famosa vulnerabilidade que
Rowhammer implementou essa mesma técnica em 2015. Mesmo depois de analisar o código de Mark, fazer a FFT funcionar foi mais difícil do que eu esperava. Mas no final, juntei todas as peças.
Primeiro você precisa preparar os dados. A FFT requer entrada com um intervalo de amostragem constante. Também queremos cortar os dados para reduzir o ruído. Por tentativa e erro, descobri que o melhor resultado é alcançado após o processamento preliminar dos dados:
- Pequenos valores (abaixo da média de 1,8) das iterações do loop são cortados, ignorados e substituídos por zeros. Realmente não queremos fazer barulho.
- Todas as outras leituras são substituídas por unidades, uma vez que a amplitude do atraso causado por algum ruído não é realmente importante para nós.
- Eu estabeleci um intervalo de amostragem de 100 ns, mas qualquer número até a frequência Nyquist (dupla frequência esperada) servirá .
- Os dados devem ser coletados em um horário fixo antes de serem enviados à FFT. Todos os métodos razoáveis de amostragem funcionam bem, decidi pela interpolação linear básica.
O algoritmo é algo como isto:
UNIT=100ns A = [(timestamp, loop_duration),...] p = 1 for curr_ts in frange(fist_ts, last_ts, UNIT): while not(A[p-1].timestamp <= curr_ts < A[p].timestamp): p += 1 v1 = 1 if avg*1.8 <= A[p-1].duration <= avg*4 else 0 v2 = 1 if avg*1.8 <= A[p].duration <= avg*4 else 0 v = estimate_linear(v1, v2, A[p-1].timestamp, curr_ts, A[p].timestamp) B.append( v )
Que em meus dados produz um vetor bastante chato como este:
[0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, ...]
No entanto, o vetor é bastante grande, geralmente cerca de 200 mil pontos de dados. Com esses dados, você pode usar o FFT!
C = numpy.fft.fft(B) C = numpy.abs(C) F = numpy.fft.fftfreq(len(B)) * (1000000000/UNIT)
Muito simples, certo? Isso produz dois vetores:
- C contém números complexos de componentes de frequência. Não estamos interessados em números complexos, e você pode suavizá-los com o comando
abs() . - F contém rótulos, cujo intervalo de frequência está em qual local do vetor C. Nós normalizamos o expoente em hertz multiplicando pela frequência de amostragem do vetor de entrada.
O resultado pode ser plotado em um gráfico:
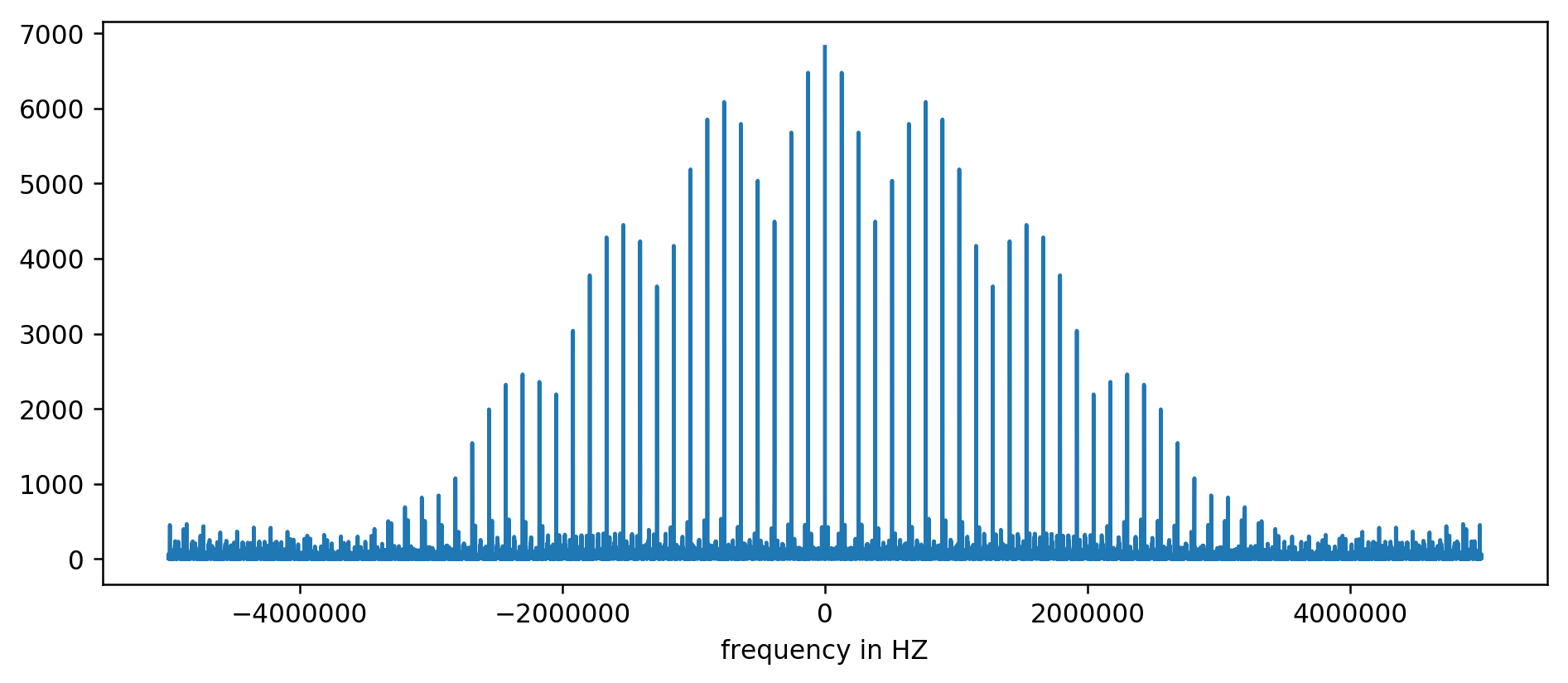
Eixo Y sem unidades, pois normalizamos o tempo de atraso. Apesar disso, as rajadas são claramente visíveis em algumas faixas de frequência fixas. Vamos considerá-los mais perto:
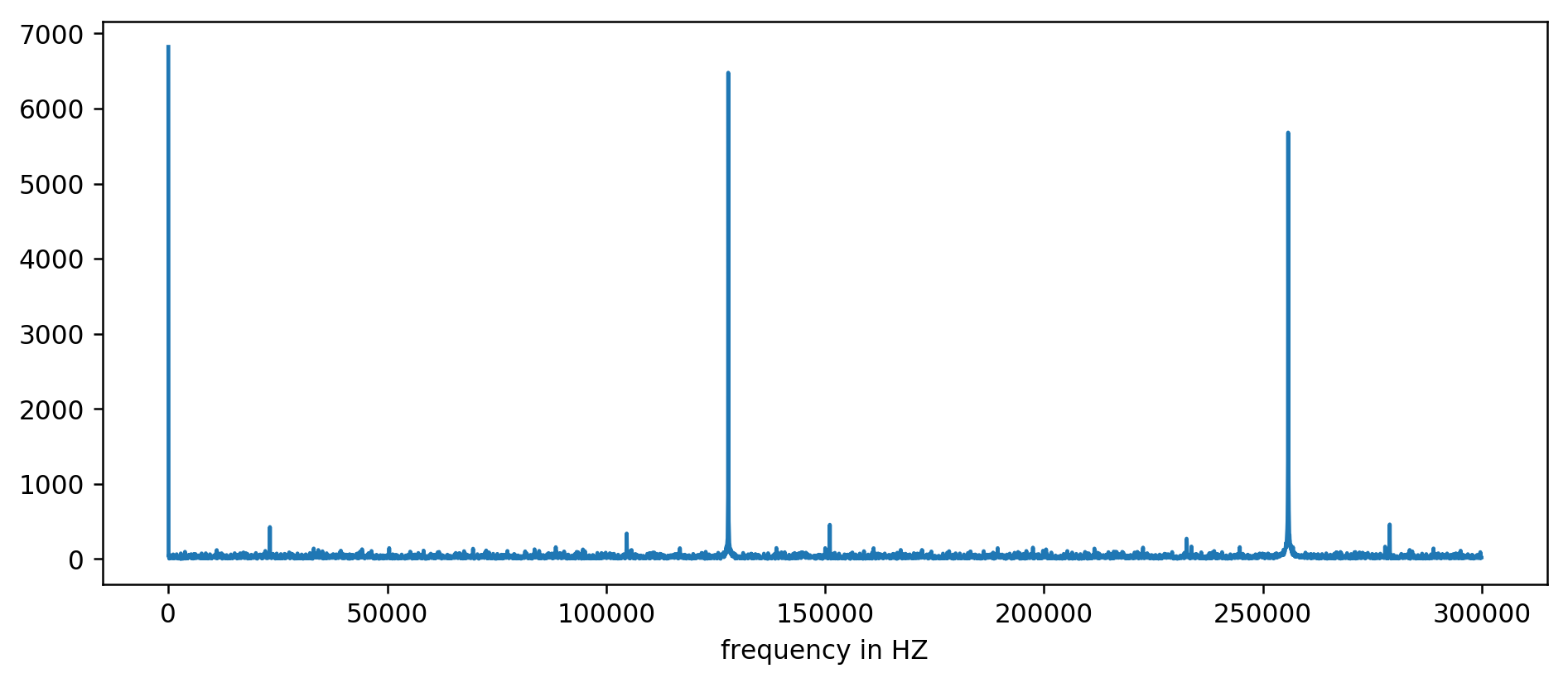
Vemos claramente os três primeiros picos. Após um pouco de aritmética inexpressiva, incluindo a leitura de filtragem pelo menos dez vezes a média, você pode extrair as frequências básicas:
127850.0
127900.0
127950.0
255700.0
255750.0
255800.0
255850.0
255900.0
255950.0
383600.0
383650.0
Consideramos: 1000000000 (ns / s) / 127900 (Hz) = 7818,6 ns
Viva! O primeiro salto na frequência é realmente o que estávamos procurando e realmente se correlaciona com o tempo de atualização.
Os picos restantes em 256 kHz, 384 kHz, 512 kHz são os chamados harmônicos que são múltiplos da nossa frequência base de 128 kHz. Esse é o efeito colateral totalmente esperado da
aplicação da FFT em algo como uma onda quadrada .
Para facilitar os experimentos, fizemos uma
versão para a linha de comando . Você pode executar o código você mesmo. Aqui está um exemplo de inicialização no meu servidor:
~ / 2018-11-refresh-memory $ make
gcc -msse4.1 -ggdb -O3 -Wall -Wextra measure-dram.c -o measure-dram
./measure-dram | python3 ./analyze-dram.py
[*] Verificando ASLR: main = 0x555555554890 pilha = 0x7fffffefe2ec
[] Curiosidade. Eu fiz 40663553 clock_gettime () por segundo
[*] Medindo o tempo MOVQ + CLFLUSH. Executando 131072 iterações.
[*] Gravando dados
[*] Dados de entrada: min = 117 avg = 176 med = 167 max = 8172 itens = 131072
[*] Intervalo de corte 212-inf
[] 127849 itens abaixo do limite, 0 itens acima do limite, 3223 itens diferentes de zero
[*] Executando FFT
[*] A frequência máxima acima de 2kHz abaixo de 250kHz tem magnitude de 7716
[+] Os picos de frequência superior a 2kHZ estão em:
127906Hz 7716
255813Hz 7947
383720Hz 7460
511626Hz 7141
Devo admitir que o código não é completamente estável. Em caso de problemas, é recomendável desativar o Turbo Boost, a escala de frequência da CPU e a otimização para desempenho.
Conclusão
Existem duas conclusões principais deste trabalho.
Vimos que os dados de baixo nível são bastante difíceis de analisar e parecem bastante barulhentos. Em vez de avaliar a olho nu, você sempre pode usar a boa e velha FFT. Na preparação dos dados, é necessário, em certo sentido, uma ilusão.
Mais importante, mostramos que muitas vezes é possível medir o comportamento sutil do hardware a partir de um processo simples no espaço do usuário. Esse tipo de pensamento levou à descoberta da
vulnerabilidade original do Rowhammer , que foi implementada nos ataques Meltdown / Spectre e novamente mostrada na recente
reencarnação do Rowhammer para a memória ECC .
Muito resta além do escopo deste artigo. Mal tocamos na operação interna do subsistema de memória. Para uma leitura mais aprofundada, recomendo:
Finalmente, aqui está uma boa descrição da antiga memória de ferrite: