Novas evidências demonstram a existência de dois tipos de curvas infinitas

O trabalho de Alexander Smith sobre a hipótese de Goldfeld revelou as propriedades fundamentais das curvas elípticas

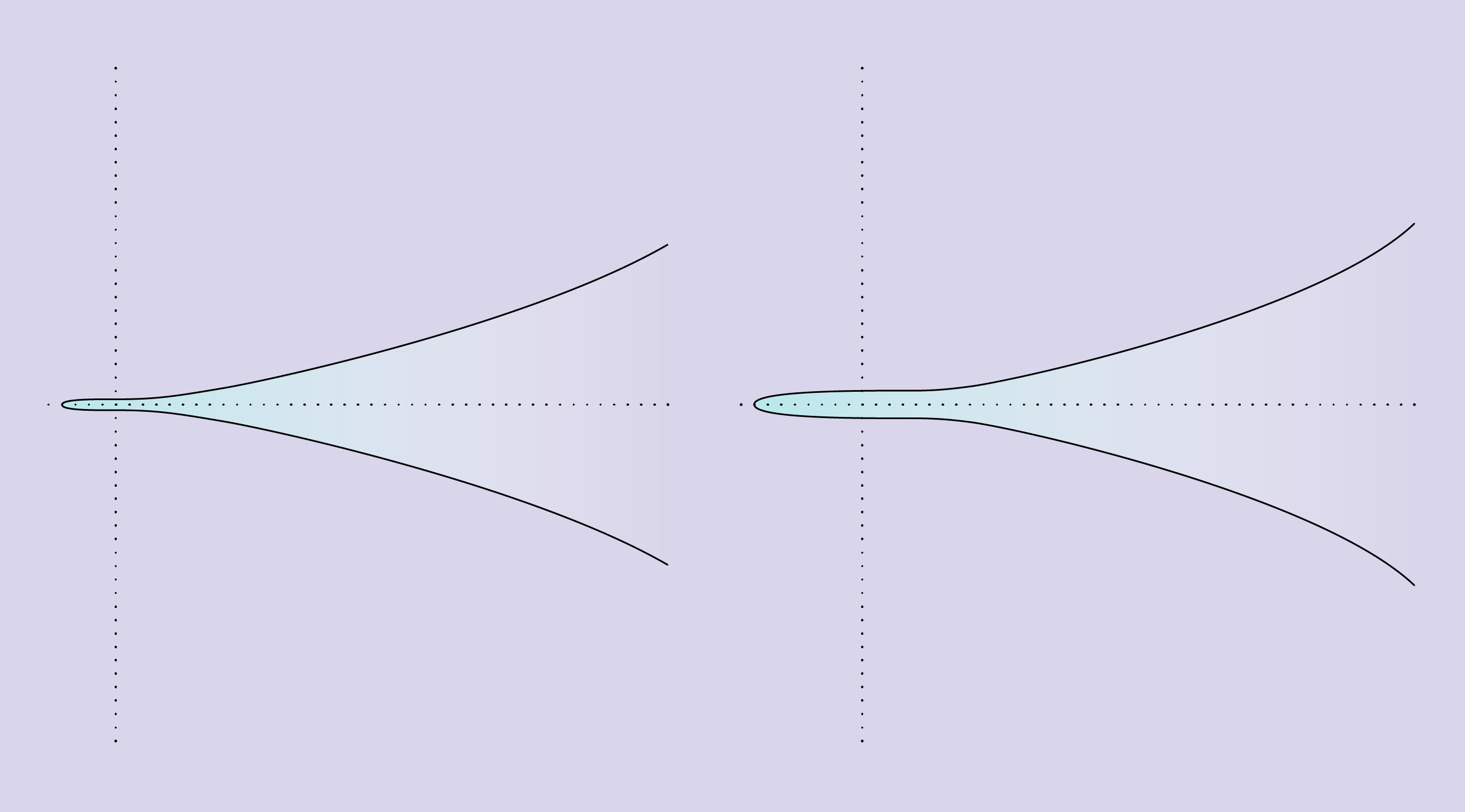Duas curvas elípticas demonstram a singularidade do conceito de classificação. A curva à esquerda é descrita pela equação y ² = x ³ + 1, passa por apenas cinco pontos racionais e tem classificação 0. A curva à direita é descrita pela equação y ² = x ³ + 8, passa por um número infinito de pontos racionais e tem classificação 1.

Pode haver muitas variantes de curvas elípticas, mas existem apenas duas de suas variedades reais. Este é o resultado das novas evidências recebidas por um estudante de graduação da Universidade de Harvard.

As curvas elípticas parecem exóticas, mas esses são objetos geométricos comuns, não mais complicados do que linhas retas, parábolas ou elipses. Em seu trabalho publicado online no ano passado, Alexadr Smith comprovou a hipótese de quarenta anos atrás sobre a característica fundamental das curvas elípticas de classificação. Smith provou que, de uma determinada família de curvas com uma característica, metade tem uma classificação de 0 e metade tem uma classificação de 1.

Esse resultado estabelece uma característica de suporte de objetos que ocuparam matemáticos por muitos séculos, cuja importância cresceu especialmente nas últimas décadas.

“Estamos pensando nisso há mais de 1000 anos e agora temos um entendimento probabilístico das curvas elípticas. Isso é extremamente importante ”, disse Shaw-Wu Zhang , matemático da Universidade de Princeton, que deu recomendações a Smith sobre seu trabalho quando ele ainda era estudante em Princeton.

As curvas elípticas são equações com variáveis ​​elevadas à terceira potência, por exemplo, y ² = x ³ + 1. Elas apareceram em muitas provas matemáticas significativas nas últimas décadas, incluindo a prova mais importante do Grande Teorema de Fermat, de 1994. Parte de seu significado está no fato de pertencerem ao tipo mais complexo de equações polinomiais, sobre o qual os matemáticos têm algum tipo de idéia sistêmica.

"As curvas elípticas são um caso interessante", disse Dorian Goldfeld , matemático da Universidade de Columbia, que propôs em 1979 uma hipótese que recebeu esse nome.

A hipótese de Goldfeld faz previsões sobre a classificação das curvas elípticas. Como já descrevemos em um artigo recente, “ Que evidência pode convencer os matemáticos se não houver prova rigorosa? ” Rank é uma medida da complexidade de um conjunto de soluções racionais de uma curva (soluções que podem ser representadas como frações). E embora não exista restrição comprovada na classificação da curva - até agora a 28 mais alta é considerada a classificação mais alta - a hipótese de Goldfeld prevê que, em média, metade das curvas elípticas tem uma classificação de 0 e a outra metade tem 1.

Pode não parecer claro para você como podem existir curvas elípticas com uma classificação maior que 1 se metade das curvas elípticas tiver uma classificação 0 e a outra metade tiver 1. Se você tiver uma caixa de bolas de pingue-pongue e se souber exatamente a metade de eles são pretos e metade são brancos, então não pode haver vermelhos.

Ainda mais confuso é o fato de que curvas elípticas com uma classificação de 2 ou superior existem não apenas algumas, mas um número infinito. O resultado aparentemente absurdo é o resultado de estatísticas astutas trabalhando com infinitos. Embora existam muitas curvas da classificação 2 e acima, existem tantas curvas com as classificações 0 e 1 que as curvas com as classificações 2 e superior não são estatisticamente significativas. Se você colocar todas as curvas em uma caixa e retirá-las aleatoriamente, as chances de fazer uma curva com uma classificação superior a 1 são oficialmente iguais a zero.

O que significa que a classificação da curva é 0? Tais curvas têm um número finito de pontos racionais - e não mais que 16, como Barry Mazur provou na década de 1970.


Dorian Goldfeld

Há razões para acreditar que um número muito grande de curvas elípticas terá uma classificação de 0. Se você imaginar como uma curva percorre um plano, será visto que a maioria dos pontos pelos quais ela passa não será racional. Esses pontos não podem ser expressos como frações, mesmo que sejam arbitrariamente complexas. As chances de uma curva aleatória cruzar muitos pontos racionais - um conjunto infinito - são pequenas.

"Eu entendi da seguinte maneira: se você usar uma curva elíptica aleatória, haverá razões para ter uma classificação de 0. Ele não quer ter argumentos racionais", disse Smith.

A prevalência das curvas de classificação 1 é explicada de maneira semelhante. As curvas de nível 1 têm infinitamente muitos pontos racionais, mas todos estão alinhados de maneira muito precisa, para que você possa conectá-los um ao outro em um processo bastante simples.

Para curvas de classificação 2 e superior, os conjuntos de pontos racionais são mais complicados. Eles contêm vários subconjuntos infinitos de pontos racionais que não estão conectados entre si.

“Quais são as chances do aparecimento de dois pontos independentes? - disse Goldfeld. "Muito baixo." Minha hipótese diz que isso deve acontecer raramente. ”

Quando Goldfeld apresentou sua hipótese, a maioria dos matemáticos a considerou incorreta. Eles apontaram para os resultados de experimentos computacionais, dos quais se seguiu que curvas com uma classificação de 2 ou superior ocorrem com muito mais frequência do que em 0% dos casos.

Goldfeld respondeu que eles simplesmente tomam o alcance muito pequeno. Ele ressaltou que se você estudar apenas os 10 primeiros números inteiros, poderá obter uma estimativa extremamente imprecisa de que 40% dos números são primos. Da mesma forma, esses experimentos computacionais extrapolaram de pequenos subconjuntos de curvas elípticas para famílias infinitamente grandes de curvas.

“Eu disse, olhe para números primos! Essa foi a minha resposta. Precisamos subir muito mais alto, porque no começo muita diversão pode aparecer ”, disse Goldfeld.

A hipótese de Goldfeld não se aplica a todas as curvas elípticas. Descreve uma família especial de curvas elípticas, torções quadráticas. Exemplo: curva elíptica cy ² = x ³ - x, onde c é uma constante. Ao alterar o valor de c, você está dobrando uma curva elíptica. A hipótese de Goldfeld refere-se a toda a variedade infinita de curvas que podem ser obtidas alterando o valor de c.

Alexander Smith testemunhou que Goldfeld estava certo. Em um novo artigo, ele prova que 100% das curvas elípticas (de um tipo especial) têm uma classificação de 0 ou 1. Ele também provou que essas curvas são igualmente divididas entre as duas fileiras, embora exista um problema. Sua prova da divisão 50–50 é baseada na validade da hipótese Birch - Swinnerton-Dyer (BJD). A hipótese BSD é um dos problemas abertos mais famosos da matemática. Os matemáticos ainda não chegaram perto de sua prova, mas no geral eles a consideram verdadeira.

Mesmo com essa ressalva, o resultado de Smith é considerado significativo. Os matemáticos dizem que ele mostra uma maneira de provar completamente a hipótese de Goldfeld sem mexer com a desanimadora hipótese de BSD. Este método fornece uma nova compreensão da natureza das curvas elípticas.

"O trabalho de Alex Smith é extremamente interessante, e acho que ainda precisa ser estudado e dado o que merece", disse Melanie Wood , matemática da Universidade de Wisconsin. "O fato de que isso possa ser provado é muito importante e revolucionário."