
Caros Khabrovchans, Apresento a vocês a continuação da pesquisa sobre o tema de encontrar sombras adequadas para um bagel 2D.
Este post é uma sequência da
publicação , uma espécie de trabalho sobre erros e o desenvolvimento da idéia.
Em seus comentários, críticos respeitados observaram, com razão, que em espaços fechados as sombras eram angulares e pouco naturais. Várias soluções foram propostas, gostei da proposta de usar a
projeção de raios para calcular a sombra.

Esclareço, não trabalho com a placa de vídeo (ainda não trabalho), todos os resultados são modelados na CPU.
Neste trabalho sobre reykasting, entendemos o método de construir uma imagem lançando raios de um observador no espaço até que ele cruze com um obstáculo (limites da tela) e destaque o local de sua colisão.
Aqui, usaremos uma versão simplificada do rakecasting com base na interseção de um bloco com um raio. Este método tem sido amplamente utilizado em jogos pseudo-tridimensionais do passado (por exemplo,
Wolfenstein_3D , respeito àqueles que estão no assunto), nós o adaptamos para o espaço bidimensional.
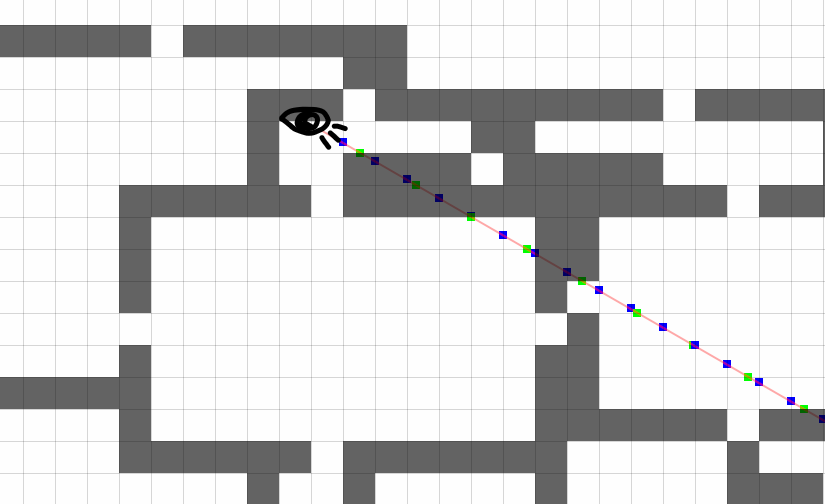
O algoritmo é simples o suficiente para entender e incorporar. Trarei minha própria implementação:
Como o feixe cruza as células em cada eixo na mesma distância, você pode economizar nos cálculos e verificar apenas se há paredes dentro do bloco. Precisamos de um cruzamento com um obstáculo e lembre-se de suas coordenadas.
Na minha implementação, coloquei todas as trigonometrias e divisões em uma tabela separada para cada ângulo, o que acelerou bastante o algoritmo.
Tendo lançado os raios em todas as direções com a etapa desejada, obtemos aproximadamente a seguinte imagem:
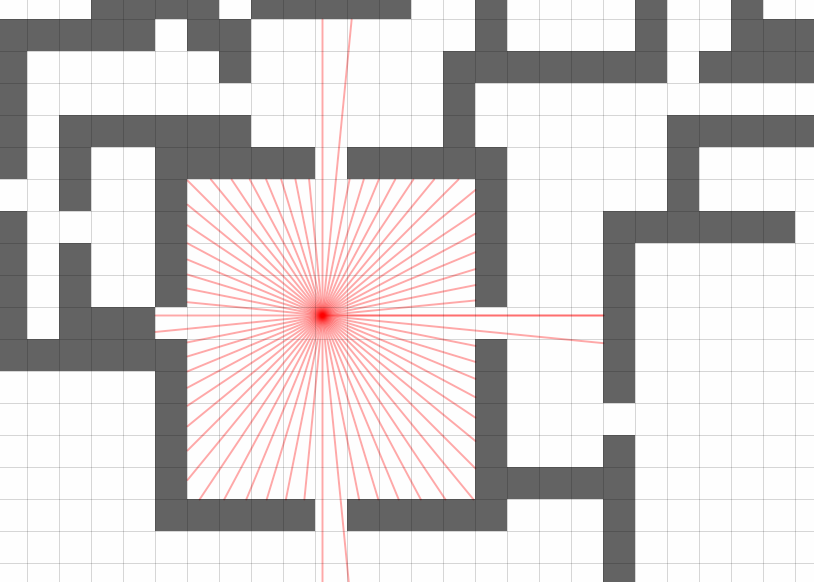
Aumentando o número de raios para vários milhares e obtendo o poliedro desejado do escopo. É possível, é claro, lançar raios para cada pixel da imagem, como nos aceleradores 3D, mas você não pode ficar sem uma placa de vídeo aqui.
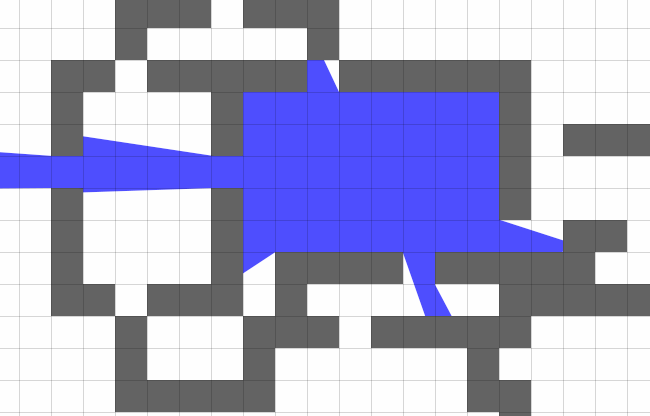
Mais trabalho com camadas começa.
Âmbito de aplicação Daí em diante, os raios passam um pouco para as profundezas dos objetos. Essa convenção de jogos cria um ambiente único, característico dos Jogos 2D.

Geração de mapa de iluminação. Geramos fontes de luz estática com antecedência e armazenamos em cache para melhorar o desempenho, aplicamos fontes dinâmicas no processo de exibição na tela.

Reunindo tudo. Tudo o que falta são monstros e tesouros terríveis ... muitos tesouros.

Paredes com uma curvatura variável da penetração da luz não foram para mim, mas talvez seja um amador.

No processo de criação do protótipo, tentei muitas variações do modelo, algumas delas mais adequadas ao
horror :
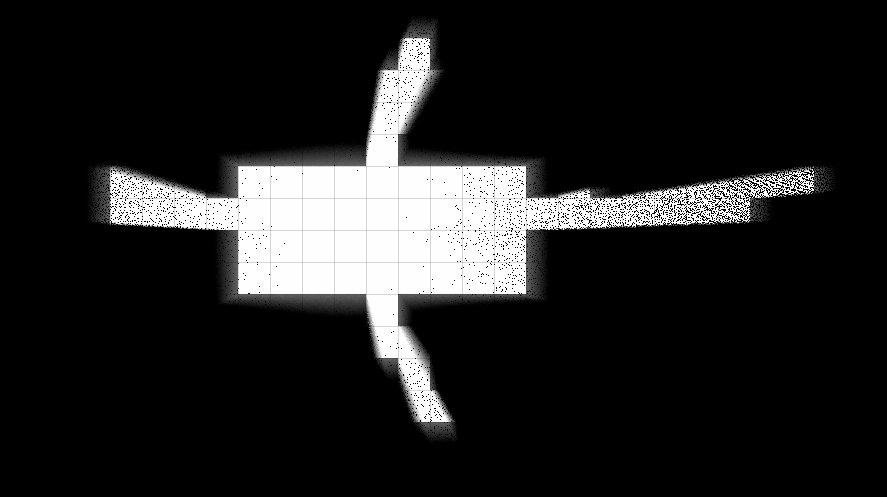
Gostei especialmente do efeito de múltiplos reflexos de raios nas paredes, mas mesmo sua implementação ingênua foi tão lenta que a deixei para o futuro quando me tornei amiga da placa de vídeo.
Obrigado pela atenção.
Link para jogar (exe para windows)
Parte 1 ,
Parte 3