Uma implementação prática do gerador de chaveamento usando o HDL da Verilog

Resumo

Os registros de troca de feedback linear são uma excelente ferramenta para implementar um gerador de bits pseudo-aleatórios no hardware; eles inibem uma estrutura eletrônica simples e eficiente. Além disso, eles são capazes de produzir sequências de saída com grandes períodos e boas propriedades estatísticas. No entanto, os LFSRs padrão não são criptograficamente seguros, uma vez que a sequência de saída pode ser prevista de forma exclusiva, dado um pequeno número de bits do fluxo de chaves usando o algoritmo Berlekamp-Massey. Vários métodos foram propostos para destruir a linearidade inerente ao projeto de LFSR. Esses métodos incluem geradores combinados não lineares, geradores de filtros não lineares e geradores controlados por relógio. No entanto, eles permanecem vulneráveis ​​a muitos ataques, como ataques de canal lateral e ataques algébricos. Em 2015, foi proposto um novo gerador controlado de ponto, chamado gerador de comutação. Foi comprovado que este novo gerador é resistente a ataques algébricos e ataques de canal lateral, preservando os requisitos de eficiência e segurança. Neste projeto, apresentamos um projeto do gerador de chaveamento usando o HDL da Verilog.

Introdução e Antecedentes Históricos

A história da geração de números pseudo-aleatórios no hardware está fortemente ligada ao desenvolvimento de cifras de fluxo. As cifras de fluxo são cifras que criptografam caracteres de texto sem formatação individualmente (geralmente bit por bit), em contraste com as cifras de bloco, que criptografam texto sem formatação em blocos grandes (64 bits ou mais). Muitas arquiteturas de cifra de fluxo requerem um gerador de fluxo de chave, que é um gerador de bits pseudo-aleatórios cuja semente é a chave de criptografia. Para cada bit de texto sem formatação, o bit de texto cifrado correspondente é calculado como uma função reversível (geralmente xor gate) do bit de texto sem formatação e o bit do fluxo de chaves correspondente. Portanto, projetar geradores de fluxo de chaves seguros e eficientes é essencial para a operação de codificação de fluxo.


Uma ferramenta útil para a construção de geradores de fluxo de chave é o registro de troca de feedback linear. Eles podem ser facilmente controlados usando componentes eletrônicos elementares e podem ser programados simplesmente em dispositivos lógicos programáveis. Além disso, devido à sua estrutura simples, os LFSRs podem ser modelados e analisados ​​matematicamente, o que levou a um vasto corpo de conhecimentos e resultados a respeito deles. A sequência de saída de um LFSR corretamente construído possui comprimento exponencial e boas propriedades estatísticas, como grande complexidade linear.


Apesar das boas propriedades estatísticas do LFSR, ele não pode ser usado como gerador de fluxo de chave em sua forma padrão devido à sua natureza linear. Se um invasor conseguiu saber $$$2L$bits consecutivos de fluxo de chave, a sequência de saída pode ser prevista de maneira única e eficiente usando o algoritmo Berlekamp-Massey, em que $$$L$é o número de registros. Muitas maneiras diferentes de destruir a linearidade inerente à sequência de saída do LFSR foram propostas:

• Usando vários LFSRs e uma função de combinação não linear de suas saídas (geradores de combinação não linear).
• Gerando a sequência de saída como alguma função não linear do estado LFSR (geradores de filtro não lineares).
• Cronometragem irregular de LFSRs (geradores controlados por relógio).

Ainda assim, todos esses projetos permaneceram vulneráveis ​​a ataques como ataques algébricos e de canal lateral. Após o ano de 2000, este não era mais um problema crítico, pois a cifra em bloco Rijndael foi proposta e eleita como Padrão Avançado de Criptografia (AES). O AES era capaz de operar no modo de cifra de fluxo e atender a todos os padrões industriais de uma cifra de fluxo. Além disso, com o aumento dos poderes computacionais, o AES poderia ser implantado em várias plataformas. Isso levou a uma diminuição significativa nos aplicativos de codificação de fluxo.


Adi Shamir apresentou uma palestra convidada no estado da arte em Stream Ciphers 2004 e Asiacrypt 2004, intitulada "Stream Ciphers: Dead or Alive?". Em sua apresentação, ele sugeriu que as cifras de fluxo podem sobreviver nas seguintes aplicações:

• Aplicativos orientados a software com velocidades excepcionalmente altas (por exemplo, roteadores).
• Aplicativos orientados a hardware com tamanho excepcionalmente pequeno (por exemplo, cartões inteligentes).

Uma das propostas mais recentes para geradores de fluxo de chaves é o gerador de chaveamento. Alega-se ser resistente a ataques algébricos e de canal lateral, preservando a eficiência e a velocidade de operação.


Neste projeto, apresentaremos um design do gerador de chaveamento em hardware, usando o HDL da Verilog. Primeiro, apresentamos as duas formas comuns de LFSRs, Fibonacci LFSRs e Galois LFSRs. A seguir, apresentamos uma apresentação matemática dos LFSRs. Em seguida, apresentaremos o gerador de chaveamento conforme apresentado por. Por fim, apresentamos nosso projeto Verilog do gerador de comutação.

Registros de mudança de feedback linear

Registros de deslocamento de realimentação linear são circuitos que consistem em uma lista linear de registros (também chamados de elementos de atraso) e um conjunto predefinido de conexão entre eles. Um sinal de relógio global (único) controla o fluxo de dados dentro do LFSR. Os dois tipos mais comuns de LFSRs usados ​​são Fibonacci LFSRs e Galois LFSRs; adiando apenas na forma de conexões. Como veremos mais adiante na seção do modelo matemático, existem muitas semelhanças entre as arquiteturas de Fibonacci e Galois, preferindo que uma sobre a outra seja específica da aplicação.


Neste artigo, assumimos um hipotético contador de tempo global começando em $$$0$e aumentando em $$$1$após cada margem positiva do ciclo do relógio global.

Registros

Um registro é um elemento lógico capaz de armazenar um bit de dados, chamado estado. Possui duas linhas de entrada: uma linha de dados de um bit e uma linha de sinal de relógio. Tem uma saída de um bit que é sempre igual ao estado interno. Em cada extremidade positiva da entrada do relógio, a entrada de dados é atribuída ao estado, caso contrário, o estado permanece inalterado. Vamos denotar o estado de um registro $$$S$no tempo $$$t$como $$$\ mathop S \ nolimits ^ t$.

Fibonacci lfsrs

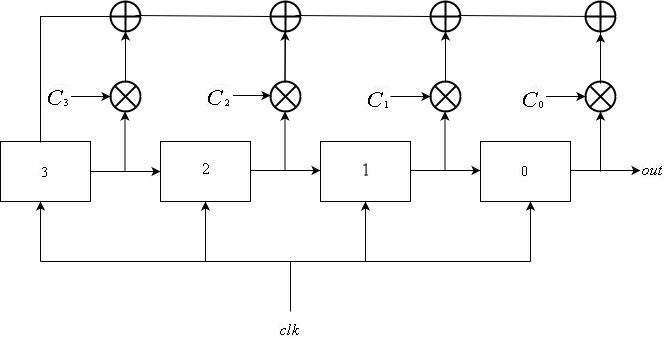
Um Fibonacci LFSR consiste em $$$L$registros enumerados de $$$0$para $$$L-1$, todos conectados ao mesmo sinal de relógio. A entrada do registro $$$i$é a saída do registro $$$i + 1$para $$$0 \ le i \ le L-2$. A entrada de feedback para o registro $$$L-1$é a soma xor das saídas de algum subconjunto de registros. A atualização do registro pode ser descrita matematicamente da seguinte maneira:

$$

$$\ mathop S \ nolimits_i ^ t = \ left \ {\ begin {array} {l} \ mathop S \ nolimits_ {i + 1} ^ {t-1} {\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ rm {se} \ \} 0 \ arquivo L-2 \\ \ mathop \ bigoplus \ limits_ {j = 1} ^ k \ mathop S \ nolimits_j ^ {t-1} \ otimes \ mathop C \ nolimits_j {\ \ \ \ \ rm {if} \ \} i = L-1 \ end {array} \ right.$$

onde $$$C_j = 1$se registrar $$$j$está incluído no feedback e $$$0$caso contrário.

A sequência de saída é obtida no registro $$$0$. Ou seja, a sequência de saída é $$$\ mathop {\ left \ {{\ mathop S \ nolimits_0 ^ i} \ right \}} \ nolimits_ {i \ ge 0}$ .

Galois LFSRs

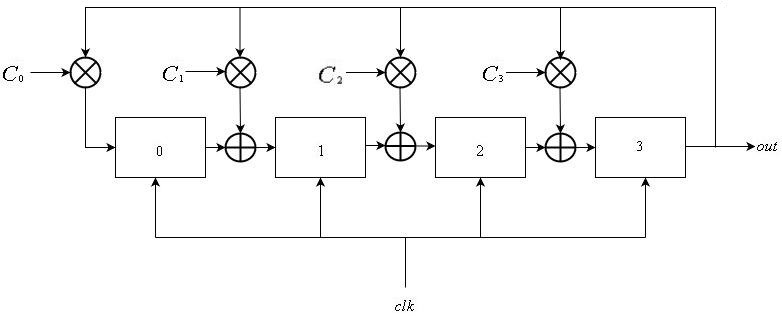
Os LFSRs de Galois também consistem em uma lista linear de $$$L$registros enumerados de $$$0$para $$$L-1$, todos compartilhando o sinal do relógio global. A entrada do registro $$$i$é a saída do registro $$$i-1$para $$$1 \ le i \ le L-1$. Para alguns subconjuntos de registradores, sua entrada é armazenada na saída do registrador $$$L-1$. Isso pode ser expresso como:

$$

$$\ mathop S \ nolimits_i ^ t = \ left \ {\ begin {array} {l} \ mathop S \ nolimits_ {i-1} ^ {t-1} \ oplus \ mathop S \ nolimits_ {L-1} ^ {t-1} \ otimes \ mathop C \ nolimits_i {\ rm {\ \ \ \ if \ \}} 1 \ le i \ le L-1 \\ \ mathop S \ nolimits_ {L-1} ^ {t- 1} \ otimes \ mathop C \ nolimits_0 {\ rm {\ \ \ \ \ \ \ \ \ \ \ \ \ if \ \}} i = 0 \ end {array} \ right.$$

onde $$$C_i = 1$se a entrada do registro $$$i$é armazenado com saída do registro $$$L-1$.


De maneira semelhante à dos LFSRs de Fibonacci, a sequência de saída é definida como $$$\ mathop {\ left \ {{\ mathop S \ nolimits_ {L-1} ^ i} \ right \}} \ nolimits_ {i \ ge 0}$ .

Comparação entre Fibonacci e Galois Designs

Existe uma correspondência direta entre Fibonacci e Galois LFSRs no sentido matemático, como veremos na próxima seção. No entanto, existem duas vantagens notáveis ​​em usar o design de Galois:

• Na implementação de software, não requer um $$$L$verificação de paridade de bits, que adiciona um fator logarítmico de complexidade.
• Na implementação de hardware, ele requer apenas portas xor de duas entradas, cujo atraso de propagação é significativamente menor que o das portas xor de várias entradas usadas no design de Fibonacci.

Em nosso projeto, consideramos a formulação matricial do LFSR, portanto, ambas as arquiteturas são intercambiáveis.

Modelo Matemático de LFSRs

Nas seções seguintes, salvo indicação em contrário, assumimos que todo o cálculo é feito sob o campo de Galois $$$Gf \ esquerda (2 \ direita)$. Ou seja, todas as operações são computadas no módulo $$$2$. Outra implementação desta convenção é que toda multiplicação é lógica e porta, e todo somatório é porta xor.


Considere os estados de todos $$$L$registros de um LFSR em algum momento $$$t$; isso pode ser representado como um vetor de $$${\ left \ {{0,1} \ right \} ^ L}$ :

$$

$${S ^ t} = \ left ({\ mathop S \ nolimits_0 ^ t; \ mathop S \ nolimits_1 ^ t; \ ldots; \ mathop S \ nolimits_ {L-1} ^ t} \ right)$$

Denotamos esse vetor como o estado do LFSR. Observe que existem no máximo $$${2 ^ L}$possíveis estados para um $$$L$registrar LFSR. Observe também que, se um LFSR atingir o estado zero, ele não poderá alcançar nenhum outro estado. Por isso dizemos que existem $$$2 ^ L-1$não trivial de um LFSR.


Considere a seguinte transformação linear:

$$

$$F = \ left ({\ begin {array} {* {20} {c}} 0 & 1 & \ cdots & 0 \\ \ vdots e \ vdots & \ ddots & \ vdots \\ 0 & 0 & \ cdots & 1 \\ {\ mathop C \ nolimits_0} e {\ mathop C \ nolimits_1} e \ cdots & {\ mathop C \ nolimits_ {L-1}} \ end {array}} \ right)$$

Dado que $$$\ mathop S \ nolimits ^ t$é o estado de um Fibonacci LFSR, pode-se observar que

$$

$$S \ nolimits F \ cdot \ mathop ^ t = \ S \ nolimits mathop ^ {t + 1}$$

Se $$$\ mathop S \ nolimits ^ t$era um estado de um Galois LFSR, então considere a transformação $$$G$:

$$

$$G = \ left ({\ begin {array} {* {20} {c}} 0 & \ cdots & 0 & {\ mathop C \ nolimits_0} \\ 1 & \ cdots & 0 & {\ mathop C \ nolimits_1} \\ \ vdots e \ ddots & \ vdots & \ vdots \\ 0 & \ cdots & 1 & {\ mathop C \ nolimits_ {L-1}} \ end {array}} \ right)$$

Nesse caso, temos

$$

$$G \ cdot \ mathop S \ nolimits ^ t = \ mathop S \ nolimits ^ {t + 1}$$

As representações matriciais de LFSRs podem ser flexíveis ao lidar com atualizações repetidas, pois podem ser interpretadas como um simples produto matricial. Pode-se observar que $$$F = {G ^ T}$. Esse fato indica as muitas semelhanças entre os desenhos de Fibonacci e Galois, se elas foram vistas como transformações lineares de $$${\ left \ {{0,1} \ right \} ^ N}$ para $$${\ left \ {{0,1} \ right \} ^ N}$ .


A multiplicação do vetor de estado de algum LFSR por uma matriz (do tipo Fiboancci ou Galois) é conhecida como cronometrar ou atualizar o LFSR.

O gerador de comutação

O Switching Generator é um gerador controlado por relógio, proposto em 2015. Está provado ter resistência a ataques algébricos e de canal lateral. Nesta seção, apresentaremos o design do gerador de chaveamento, conforme especificado por seus inventores.

Estrutura básica

O gerador de chaveamento consiste em dois LFSRs: um LFSR de controle $$$A$de comprimento $$$N$e um LFSR de dados $$$B$de comprimento $$$M$. O controle LFSR é atualizado conforme descrito anteriormente. No entanto, o LFSR de dados é atualizado usando uma das duas matrizes possíveis, $$$\ mathop M \ nolimits_1 ^ i$ou $$$\ mathop M \ nolimits_2 ^ j$onde $$${M_1}, {M_2}$são matrizes companheiras de alguns polinômios primitivos. A escolha de uma matriz sobre a outra é determinada pela saída do sinal do controle LFSR. Este processo pode ser descrito da seguinte maneira:

$$

$$\ mathop B \ nolimits ^ t = \ left \ {\ begin {array} {l} \ mathop M \ nolimits_1 ^ i \ cdot \ mathop B \ nolimits ^ {t-1} {\ rm {\ \ \ \ \ \}} \ mathop A \ nolimits_ {M-1} ^ t = 0 \\ \ mathop M \ nolimits_2 ^ j \ cdot \ mathop B \ nolimits ^ {t-1} {\ rm {\ \ \ \ if \ \}} \ mathop A \ nolimits_ {M-1} ^ t = 1 \ end {array} \ right.$$

A saída do gerador de chaveamento é a saída do LFSR $$$B$. Observe que assumimos que $$$A$é um GalFS LFSR. Pode ser também um LFSR de Fibonacci.


Inteiros $$$i, j$São chamados de índices de comutação.

A semente

Lembre-se de que um LFSR pode iterar no máximo $$${2 ^ L} -1$estados não triviais antes de revisar estados anteriores. Desde matrizes $$${M_1}, {M_2}$são matrizes de transformação de LFSRs, podemos deduzir que números inteiros $$$i, j$pode ser no máximo $$$2 ^ M-1$antes que as matrizes comecem a repetir.


A semente do gerador de comutação é $$$N + 3M$bits, representando os estados iniciais dos LFSRs $$$A$e $$$B$e os poderes inteiros $$$i, j$. Observe que matrizes $$${M_1}, {M_2}$são corrigidos durante a implementação e não são incluídos na semente.

Verilog design

Nesta seção, apresentaremos nosso projeto do gerador de chaveamento usando o HDL da Verilog. Apresentaremos todos os projetos de módulos de maneira ascendente. No final, apresentamos o módulo gerador de comutação.


Em nosso projeto, tentamos reduzir ao mínimo os componentes síncronos. Os únicos componentes controlados por relógio são os LFSRs $$$A, B$.


As operações de matriz e vetor podem ser implementadas em vários métodos diferentes, variando no consumo de unidades lógicas, unidades de memória e complexidade processual. Em nosso design, eliminamos a necessidade de blocos procedimentais e usamos elementos lógicos ao máximo.


Todas as matrizes nos seguintes módulos são indexadas a partir de $$$0$esquerda para a direita e, em seguida, de cima para baixo.


Observe também que todos os módulos possuem tamanhos parametrizados; isso é para fins de depuração. Em uma implementação real, todos os tamanhos são fixos.

Multiplexador

Este é um módulo implementando um 2 para 1 $$$N$multiplexador de bits. O módulo possui dois $$$N$de entrada de 4 bits, uma linha seletora de 1 bit e $$$N$linha de saída de bits. Se a entrada do seletor for $$$0$a saída é definida para a primeira linha de entrada, caso contrário, é definida para a segunda.


Módulo multiplexador

Transformação vetorial

Este módulo implementa uma transformação linear em um vetor. Aceita como entrada um $$$N \ vezes N$matriz de transformação e uma $$$N$vetor de bits. Ele gera o produto vetor de matriz de sua entrada.


Cada bit no vetor de saída é o resultado de um $$$N$xor-gate, tomando como entrada o resultado do $$$N$bit a bit e do vetor de entrada e a linha da matriz correspondente. Ou seja, cada bit de saída é conectado à entrada e nenhum bloco de procedimento é necessário.


Exatamente $$$N ^ 2$duas entradas e portas são usadas, junto com $$$N$$$$N$portas xor de entrada.


Módulo de transformação vetorial

Identidade

Este módulo não aceita entrada. É $$$N \ vezes N$saída de bits é inicializada no $$$N$matriz de identidade. Esse módulo é declarado por conveniência, para que não tenhamos que inicializar um vetor de registro global para cada tamanho diferente.


Módulo de matriz de identidade

Transpor

Este módulo aceita um $$$N \ vezes N$matriz e produzir sua transposição. Não são utilizados elementos lógicos nem de memória neste módulo, sua saída é apenas uma permutação de sua entrada
.

Matrix Transpose Module

Multiplicação de matrizes

Este é um módulo implementando multiplicação matriz-matriz. Aceita dois $$$N \ vezes N$matrizes como entrada e produz seu produto matriz-matriz.


Este módulo contém uma instância do módulo de transposição da matriz. Isso possibilita atribuir índices consecutivos a colunas na segunda matriz de entrada. Cada entrada na matriz de saída é então atribuída à saída de um $$$N$-input xor gate, cuja entrada é o bit a bit e da linha correspondente da primeira matriz e coluna da segunda.


Exatamente $$$N ^ 3$duas entradas e portões e $$$N ^ 2$$$$N$-input xor são usados ​​nesta implementação.


Módulo de multiplicação de matrizes

Exponenciação de Matriz

Este módulo eleva uma matriz a uma potência inteira. Aceita como entrada um $$$N \ vezes N$matriz e um $$$K$inteiro de bits. Sua saída é a matriz elevada para a potência inteira especificada.


Módulo de exponenciação de matriz

Unidade de controle

Este módulo implementa o $$$N$controle de bits LFSR. É um dos dois módulos controlados por relógio em nosso design.


Inclui uma estática $$$N \ vezes N$Matriz de transformação LFSR e uma variável $$$N$estado de bits. Sua entrada inclui um relógio, um $$$N$redefinição de estado de bits e um sinal de redefinição. Sua saída é um único bit, que é o último bit do LFSR.


Após cada extremidade positiva do sinal do relógio, o estado é atualizado de acordo com a matriz de transformação usando um módulo de multiplicação de vetores matriciais. A redefinição do estado é atribuída ao estado interno após cada extremidade positiva do sinal de redefinição.





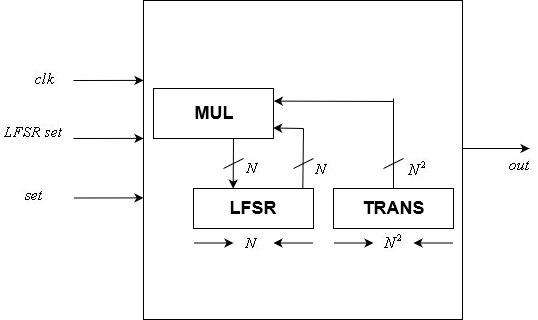Módulo da unidade de controle

Unidade de dados

O $$$N$dados LFSR é implementado usando este módulo. Como o módulo da unidade de controle, é controlado por relógio


O módulo inclui dois $$$N \ vezes N$matrizes de transformação e uma $$$N$estado LFSR de bits. Aceita como entrada um sinal de relógio, um sinal de controle, um $$$N$redefinição de estado LFSR de dois bits, dois $$$N \ vezes N$a transformação da matriz é redefinida e um sinal de redefinição. Possui uma saída de um bit, o último bit do LFSR interno.


Observe que, como a semente pode ser alterada, as matrizes de transformação também podem ser alteradas, diferentemente da unidade de controle cuja matriz de transformação é fixa.




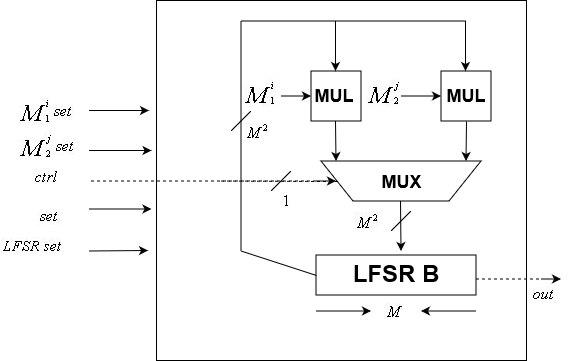\ Unidade de Dados

O gerador de comutação

Este é o módulo principal do nosso design. É parametrizado por números inteiros $$$N, M$, que são os tamanhos das unidades de controle e dados, respectivamente.


A entrada para este módulo é um sinal de relógio, um $$$N + 3M$semente de bits e um sinal definido. A semente é simplesmente uma concatenação da redefinição do LFSR de controle, da redefinição do LFSR dos dados e de números inteiros $$$i, j$Sua saída é de um bit, o pseudo-aleatório bit gerado pelo gerador de comutação.


Este módulo inclui dois $$$M \ vezes M$matrizes $$$\ mathop M \ nolimits_1, \ mathop M \ nolimits_2$. Essas matrizes são corrigidas durante a implementação.


Duas instâncias de módulos de exponenciação de matriz são usadas para calcular as matrizes de entrada para a unidade de dados, onde suas entradas são as matrizes de transformação fixas e números inteiros $$$i, j$, extraído da semente.


O módulo gerador de comutação

Conclusões e recomendações

Neste projeto, apresentamos um design do gerador de chaveamento usando o HDL da Verilog. Esse design é focado inteiramente no hardware e elimina o uso de blocos de procedimentos. Essa abordagem permite o desempenho máximo às custas dos elementos lógicos e de memória. Para alguns aplicativos com restrições de elementos lógicos e de memória, pode ser benéfico sacrificar o desempenho e aumentar o uso de blocos de procedimentos para reduzir o uso de elementos eletrônicos.


Uma desvantagem do projeto é que ele assume a responsabilidade de escolher bons índices de alternância para o usuário. Um possível avanço é adicionar um componente de hardware para verificar a validade do índice de comutação usado. Isso requer uma implementação de hardware de algoritmos complexos, como encontrar o polinômio das características de uma matriz e verificar sua primitividade.


Um possível avanço é adicionar um gerador de números aleatórios verdadeiro para verificar índices de comutação aleatórios e emitir um par válido assim que for encontrado. Pode-se provar que esse processo é interrompido após um curto período de tempo com alta probabilidade.

Referências

1. Katz, Jonathan e outros. Manual de criptografia aplicada. Imprensa CRC, 1996.
2. Choi, Jun, et al. "O gerador de chaveamento: novo gerador controlado por relógio com resistência contra ataques algébricos e de canal lateral". Entropy 17.6 (2015): 3692-3709.
3. Shamir, Adi. "Cifras de fluxo: mortas ou vivas?." ASIACRYPT. 2004.
4. LFSRs para os não iniciados