O artigo está escrito sobre a análise e estudo de materiais da competição para a busca de navios no mar.

Vamos tentar entender como e o que a rede está procurando e o que encontra. Este artigo é simplesmente o resultado de curiosidade e interesse ocioso, nada disso é encontrado na prática e, para tarefas práticas, não há nada para copiar e colar. Mas o resultado não é totalmente esperado. A Internet está cheia de descrições da operação de redes nas quais os autores descrevem lindamente e com imagens como as redes determinam primitivas - ângulos, círculos, bigodes, caudas, etc., e depois são pesquisadas por segmentação / classificação. Muitas competições são vencidas usando pesos de outras redes grandes e amplas. É interessante entender e ver como e quais primitivas uma rede constrói.
Realizaremos um pequeno estudo e consideraremos as opções - o raciocínio e o código do autor são apresentados, você pode verificar / complementar / alterar tudo sozinho.
A competição de busca marinha kaggle terminou recentemente. A Airbus propôs analisar imagens de satélite do mar com e sem navios. No total, 192555 imagens 768x768x3 - são 340 720 680 960 bytes se uint8 e quatro vezes mais que float32 (a propósito float32 é mais rápido que float64, menos acesso à memória) e em 15606 fotos é necessário encontrar naves. Como de costume, todos os lugares significativos foram ocupados por pessoas envolvidas no ODS (ods.ai), o que é natural e esperado, e espero que em breve possamos estudar a linha de pensamento e o código dos vencedores e vencedores dos prêmios.
Vamos considerar um problema semelhante, mas simplificá-lo significativamente - pegue o mar np.random.sample () * 0,5, não precisamos de ondas, vento, praias e outros padrões e rostos ocultos. Vamos tornar a imagem do mar realmente aleatória na faixa de RGB de 0,0 a 0,5. Vamos colorir os vasos da mesma cor e, para distingui-los do mar, colocá-los no intervalo de 0,5 a 1,0, e todos terão a mesma forma - elipses de diferentes tamanhos e orientações.

Pegue uma versão muito comum da rede (você pode usar sua rede favorita) e faremos todos os experimentos com ela.
Em seguida, alteraremos os parâmetros da imagem, criaremos interferências e construiremos hipóteses - para destacar as principais características pelas quais a rede encontra elipses. Talvez o leitor tire suas conclusões e refute o autor.
Carregamos bibliotecas, determinamos os tamanhos de uma matriz de imagensimport numpy as np import pandas as pd import matplotlib.pyplot as plt %matplotlib inline import math from tqdm import tqdm_notebook, tqdm from skimage.draw import ellipse, polygon from keras import Model from keras.callbacks import EarlyStopping, ModelCheckpoint, ReduceLROnPlateau from keras.models import load_model from keras.optimizers import Adam from keras.layers import Input, Conv2D, Conv2DTranspose, MaxPooling2D, concatenate, Dropout from keras.losses import binary_crossentropy import tensorflow as tf import keras as keras from keras import backend as K from tqdm import tqdm_notebook w_size = 256 train_num = 8192 train_x = np.zeros((train_num, w_size, w_size,3), dtype='float32') train_y = np.zeros((train_num, w_size, w_size,1), dtype='float32') img_l = np.random.sample((w_size, w_size, 3))*0.5 img_h = np.random.sample((w_size, w_size, 3))*0.5 + 0.5 radius_min = 10 radius_max = 30
determinar as funções de perda e precisão def dice_coef(y_true, y_pred): y_true_f = K.flatten(y_true) y_pred = K.cast(y_pred, 'float32') y_pred_f = K.cast(K.greater(K.flatten(y_pred), 0.5), 'float32') intersection = y_true_f * y_pred_f score = 2. * K.sum(intersection) / (K.sum(y_true_f) + K.sum(y_pred_f)) return score def dice_loss(y_true, y_pred): smooth = 1. y_true_f = K.flatten(y_true) y_pred_f = K.flatten(y_pred) intersection = y_true_f * y_pred_f score = (2. * K.sum(intersection) + smooth) / (K.sum(y_true_f) + K.sum(y_pred_f) + smooth) return 1. - score def bce_dice_loss(y_true, y_pred): return binary_crossentropy(y_true, y_pred) + dice_loss(y_true, y_pred) def get_iou_vector(A, B):
Usamos a métrica clássica na segmentação de imagens, existem muitos artigos, código com comentários e texto sobre a métrica selecionada, no mesmo kaggle existem muitas opções com comentários e explicações. Vamos prever a máscara do pixel - este é o "mar" ou o "barco" e avaliaremos a verdade ou falsidade da previsão. I.e. As quatro opções a seguir são possíveis - previmos corretamente que um pixel é um "mar", previmos corretamente que um pixel é um "navio" ou cometemos um erro ao prever um "mar" ou um "navio". E assim, para todas as imagens e todos os pixels, estimamos o número das quatro opções e calculamos o resultado - este será o resultado da rede. E quanto menos previsões errôneas e mais verdadeiras, mais preciso o resultado e melhor a rede.
E para a pesquisa, vamos usar a bem estudada u-net, que é uma excelente rede para segmentação de imagens. A rede é muito comum nessas competições e existem muitas descrições, sutilezas de aplicação, etc. Foi escolhida uma variante da rede U clássica e, é claro, foi possível atualizá-la, adicionar blocos residuais etc. Mas "você não pode abraçar a imensidão" e realizar todas as experiências e testes de uma só vez. O U-net realiza uma operação muito simples com imagens - reduz o tamanho da imagem com algumas transformações passo a passo e, em seguida, tenta recuperar a máscara da imagem compactada. I.e. a dimensão da imagem em nosso caso é aumentada para 32x32 e, em seguida, tentamos restaurar a máscara usando dados de todas as compressões anteriores.
Na figura, o esquema U-net é do artigo original, mas o refizemos um pouco, mas a essência permanece a mesma - compactamos a imagem → expandimos para uma máscara.
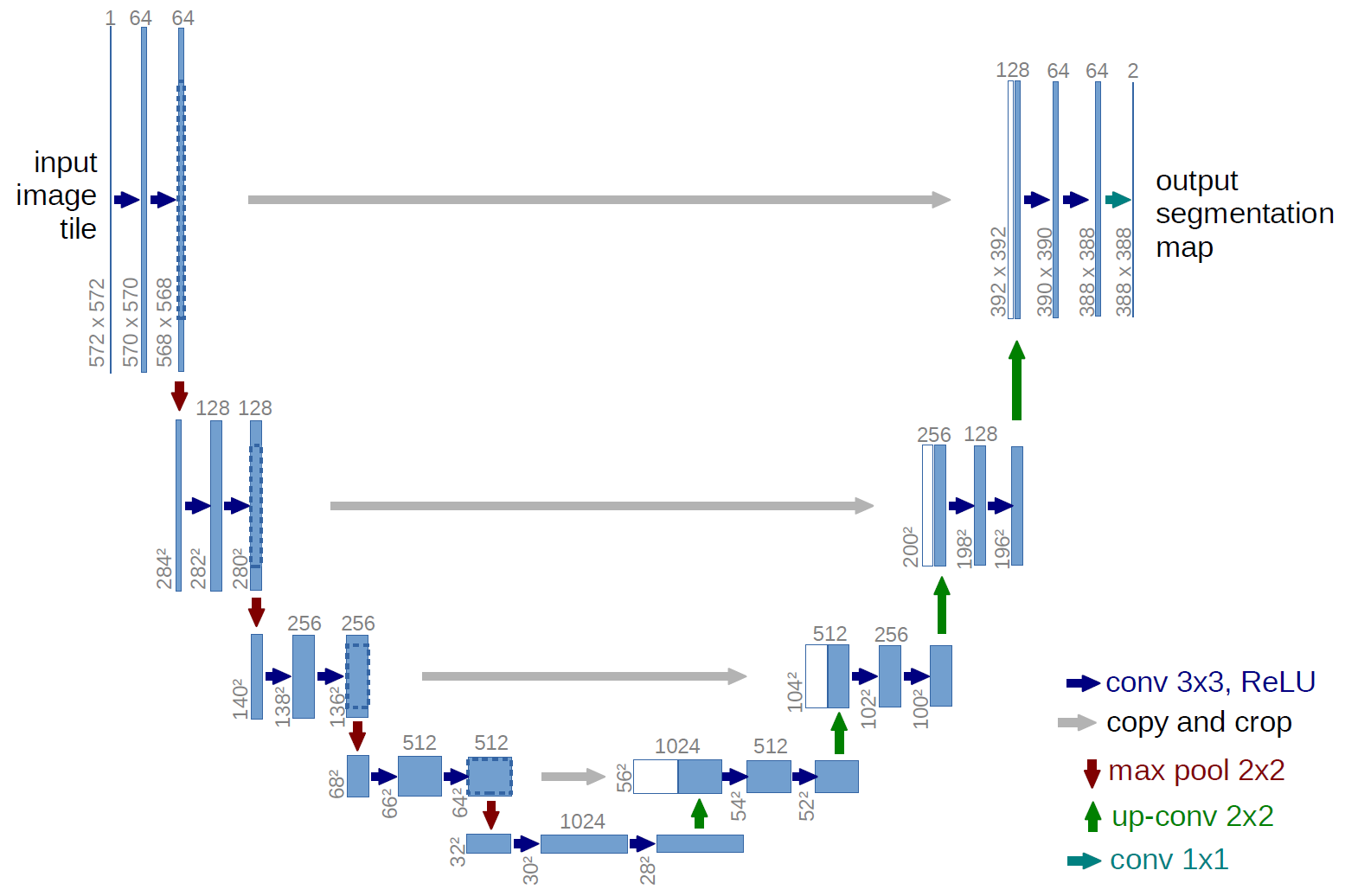
Apenas U-net def build_model(input_layer, start_neurons): conv1 = Conv2D(start_neurons*1,(3,3),activation="relu", padding="same")(input_layer) conv1 = Conv2D(start_neurons*1,(3,3),activation="relu", padding="same")(conv1) pool1 = MaxPooling2D((2, 2))(conv1) pool1 = Dropout(0.25)(pool1) conv2 = Conv2D(start_neurons*2,(3,3),activation="relu", padding="same")(pool1) conv2 = Conv2D(start_neurons*2,(3,3),activation="relu", padding="same")(conv2) pool2 = MaxPooling2D((2, 2))(conv2) pool2 = Dropout(0.5)(pool2) conv3 = Conv2D(start_neurons*4,(3,3),activation="relu", padding="same")(pool2) conv3 = Conv2D(start_neurons*4,(3,3),activation="relu", padding="same")(conv3) pool3 = MaxPooling2D((2, 2))(conv3) pool3 = Dropout(0.5)(pool3) conv4 = Conv2D(start_neurons*8,(3,3),activation="relu", padding="same")(pool3) conv4 = Conv2D(start_neurons*8,(3,3),activation="relu", padding="same")(conv4) pool4 = MaxPooling2D((2, 2))(conv4) pool4 = Dropout(0.5)(pool4)
Primeiro experimento. Mais fácil
A primeira versão do nosso experimento foi escolhida para simplificar a simplicidade - o mar está mais claro, os navios estão mais escuros. Tudo é muito simples e óbvio, sugerimos que a rede encontre naves / elipses sem problemas e com precisão. A função next_pair gera um par de figura / máscara, no qual o local, tamanho, ângulo de rotação são selecionados aleatoriamente. Além disso, todas as alterações serão feitas nessa função - uma alteração na coloração, forma, interferência etc. Mas agora a opção mais fácil, testamos a hipótese de barcos escuros sobre um fundo claro.
def next_pair(): p = np.random.sample() - 0.5
Geramos o trem inteiro e vemos o que aconteceu. Parece barcos no mar e nada mais. Tudo é claramente visível, claro e compreensível. A localização é aleatória e há apenas uma elipse em cada imagem.
for k in range(train_num):
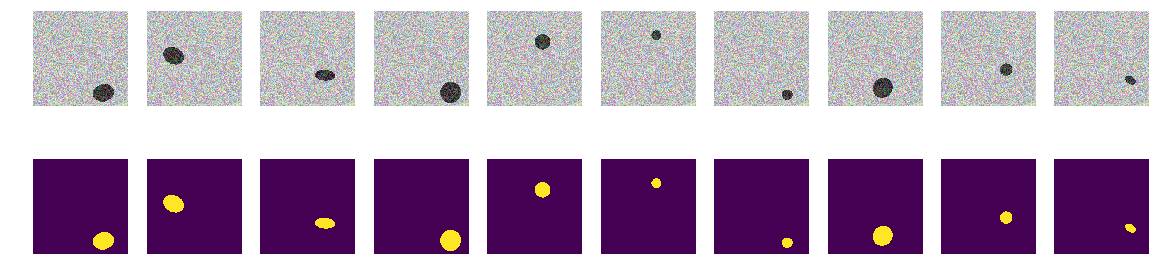
Não há dúvida de que a rede aprenderá com êxito e encontrará elipses. Mas vamos testar nossa hipótese de que a rede é treinada para encontrar elipses / naves e, ao mesmo tempo, com alta precisão.
input_layer = Input((w_size, w_size, 3)) output_layer = build_model(input_layer, 16) model = Model(input_layer, output_layer) model.compile(loss=bce_dice_loss, optimizer=Adam(lr=1e-3), metrics=[my_iou_metric]) model.save_weights('./keras.weights') while True: history = model.fit(train_x, train_y, batch_size=32, epochs=1, verbose=1, validation_split=0.1 ) if history.history['my_iou_metric'][0] > 0.75: break
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 55s 7ms/step - loss: 0.2272 - my_iou_metric: 0.7325 - val_loss: 0.0063 - val_my_iou_metric: 1.0000
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 53s 7ms/step - loss: 0.0090 - my_iou_metric: 1.0000 - val_loss: 0.0045 - val_my_iou_metric: 1.0000
A rede encontra elipses com sucesso. Mas não está de todo provado que ela está procurando elipses na compreensão do homem, como uma região delimitada pela equação da elipse e cheia de conteúdo diferente do plano de fundo, não há certeza de que haja pesos de rede semelhantes aos coeficientes da equação da elipse quadrática. E é óbvio que o brilho da elipse é menor que o brilho do fundo e não é segredo ou enigma - assumimos que acabamos de verificar o código. Vamos corrigir o rosto óbvio, fazer o fundo e a cor da elipse aleatórios também.
Segunda opção
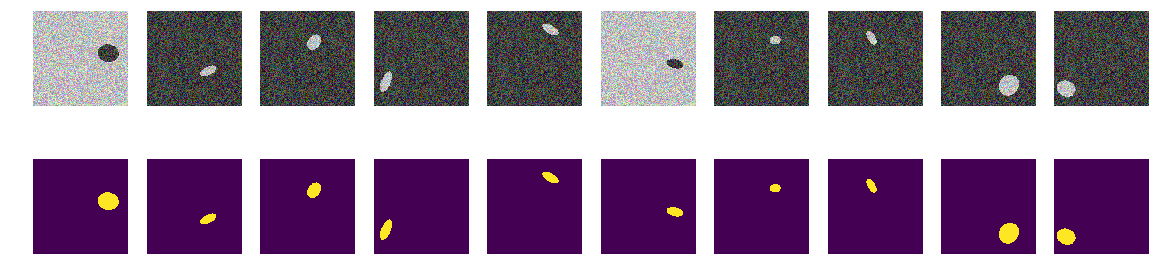
Agora, as mesmas elipses estão no mesmo mar, mas a cor do mar e, consequentemente, o barco são escolhidos aleatoriamente. Se o mar estiver mais escuro, o navio será mais leve e vice-versa. I.e. pelo brilho do grupo de pontos, é impossível determinar se eles estão fora da elipse, ou seja, o mar ou esses são pontos dentro da elipse. Novamente, testamos nossa hipótese de que a rede encontrará elipses independentemente da cor.
def next_pair(): p = np.random.sample() - 0.5
Agora, pelo pixel e seus arredores, é impossível determinar o plano de fundo ou a elipse. Também geramos imagens e máscaras e observamos os 10 primeiros na tela.
máscaras de construção for k in range(train_num): img, msk = next_pair() train_x[k] = img train_y[k] = msk fig, axes = plt.subplots(2, 10, figsize=(20, 5)) for k in range(10): axes[0,k].set_axis_off() axes[0,k].imshow(train_x[k]) axes[1,k].set_axis_off() axes[1,k].imshow(train_y[k].squeeze())
input_layer = Input((w_size, w_size, 3)) output_layer = build_model(input_layer, 16) model = Model(input_layer, output_layer) model.compile(loss=bce_dice_loss, optimizer=Adam(lr=1e-3), metrics=[my_iou_metric]) model.load_weights('./keras.weights', by_name=False) while True: history = model.fit(train_x, train_y, batch_size=32, epochs=1, verbose=1, validation_split=0.1 ) if history.history['my_iou_metric'][0] > 0.75: break
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 56s 8ms/step - loss: 0.4652 - my_iou_metric: 0.5071 - val_loss: 0.0439 - val_my_iou_metric: 0.9005
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 55s 7ms/step - loss: 0.1418 - my_iou_metric: 0.8378 - val_loss: 0.0377 - val_my_iou_metric: 0.9206A rede lida e encontra facilmente todas as elipses. Mas aqui, há uma falha na implementação e tudo é óbvio - a menor das duas áreas na imagem é uma elipse, outro fundo. Talvez essa seja uma hipótese falsa, mas ainda assim conserte-a, adicione outro polígono à imagem da mesma cor que a elipse.
Terceira opção
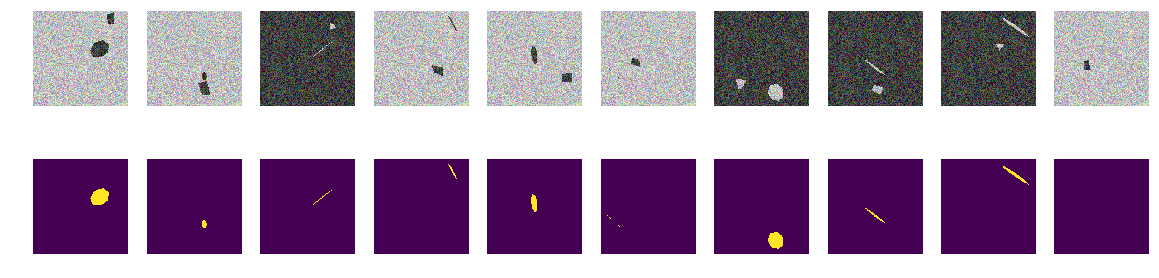
Em cada figura, escolhemos aleatoriamente a cor do mar entre as duas opções e adicionamos uma elipse e um retângulo, ambos diferentes da cor do mar. Acontece o mesmo “mar”, também um “barco” pintado, mas na mesma imagem adicionamos um retângulo da mesma cor que o “barco” e também com um tamanho selecionado aleatoriamente. Agora, nossa suposição é mais complicada, na figura existem dois objetos de cores idênticas, mas supomos que a rede ainda aprenderá a escolher o objeto certo.
programa para desenhar elipses e retângulos Como antes, calculamos imagens e máscaras e observamos os 10 primeiros pares.
construção máscara fotos elipses e retângulos for k in range(train_num): img, msk = next_pair() train_x[k] = img train_y[k] = msk fig, axes = plt.subplots(2, 10, figsize=(20, 5)) for k in range(10): axes[0,k].set_axis_off() axes[0,k].imshow(train_x[k]) axes[1,k].set_axis_off() axes[1,k].imshow(train_y[k].squeeze())

input_layer = Input((w_size, w_size, 3)) output_layer = build_model(input_layer, 16) model = Model(input_layer, output_layer) model.compile(loss=bce_dice_loss, optimizer=Adam(lr=1e-3), metrics=[my_iou_metric]) model.load_weights('./keras.weights', by_name=False) while True: history = model.fit(train_x, train_y, batch_size=32, epochs=1, verbose=1, validation_split=0.1 ) if history.history['my_iou_metric'][0] > 0.75: break
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 57s 8ms/step - loss: 0.7557 - my_iou_metric: 0.0937 - val_loss: 0.2510 - val_my_iou_metric: 0.4580
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 55s 7ms/step - loss: 0.0719 - my_iou_metric: 0.8507 - val_loss: 0.0183 - val_my_iou_metric: 0.9812Não foi possível confundir os retângulos da rede e nossa hipótese é confirmada. A julgar por exemplos e discussões, todos na competição da Airbus tinham navios únicos e vários navios estavam próximos com bastante precisão. A elipse do retângulo - ou seja, o navio é da casa na praia, a rede se distingue, mesmo que os polígonos sejam da mesma cor das elipses. Não é uma questão de cor, pois a elipse e o retângulo são igualmente pintados aleatoriamente.
Quarta opção
Talvez a rede seja diferenciada por retângulos - corrija, distorça-os. I.e. a rede encontra facilmente as duas áreas fechadas, independentemente da forma, e descarta a que é um retângulo. Essa é a hipótese do autor - vamos verificá-la, para a qual adicionaremos não retângulos, mas polígonos quadrangulares de forma arbitrária. E, novamente, nossa hipótese é que a rede distingue uma elipse de um polígono quadrangular arbitrário da mesma cor.
É claro que você pode entrar no interior da rede e observar as camadas e analisar o significado de pesos e mudanças. O autor está interessado no comportamento resultante da rede, o julgamento será baseado no resultado do trabalho, embora seja sempre interessante olhar para dentro.
fazer alterações na geração de imagens def next_pair(): p = np.random.sample() - 0.5 r = np.random.sample()*(w_size-2*radius_max) + radius_max c = np.random.sample()*(w_size-2*radius_max) + radius_max r_radius = np.random.sample()*(radius_max-radius_min) + radius_min c_radius = np.random.sample()*(radius_max-radius_min) + radius_min rot = np.random.sample()*360 rr, cc = ellipse( r, c, r_radius, c_radius, rotation=np.deg2rad(rot), shape=img_l.shape ) p0 = np.rint(np.random.sample()*(radius_max-radius_min) + radius_min) p1 = np.rint(np.random.sample()*(w_size-radius_max)) p2 = np.rint(np.random.sample()*(w_size-radius_max)) p3 = np.rint(np.random.sample()*2.*radius_min - radius_min) p4 = np.rint(np.random.sample()*2.*radius_min - radius_min) p5 = np.rint(np.random.sample()*2.*radius_min - radius_min) p6 = np.rint(np.random.sample()*2.*radius_min - radius_min) p7 = np.rint(np.random.sample()*2.*radius_min - radius_min) p8 = np.rint(np.random.sample()*2.*radius_min - radius_min) poly = np.array(( (p1, p2), (p1+p3, p2+p4+p0), (p1+p5+p0, p2+p6+p0), (p1+p7+p0, p2+p8), (p1, p2), )) rr_p, cc_p = polygon(poly[:, 0], poly[:, 1], img_l.shape) in_sc = list(set(rr) & set(rr_p)) if len(in_sc) > 0: if np.mean(rr_p) > np.mean(in_sc): poly += np.max(in_sc) - np.min(in_sc) else: poly -= np.max(in_sc) - np.min(in_sc) rr_p, cc_p = polygon(poly[:, 0], poly[:, 1], img_l.shape) if p > 0: img = img_l.copy() img[rr, cc] = img_h[rr, cc] img[rr_p, cc_p] = img_h[rr_p, cc_p] else: img = img_h.copy() img[rr, cc] = img_l[rr, cc] img[rr_p, cc_p] = img_l[rr_p, cc_p] msk = np.zeros((w_size, w_size, 1), dtype='float32') msk[rr, cc] = 1. return img, msk
Calculamos imagens e máscaras e observamos os 10 primeiros pares.
construímos imagens máscaras elipses e polígonos for k in range(train_num): img, msk = next_pair() train_x[k] = img train_y[k] = msk fig, axes = plt.subplots(2, 10, figsize=(20, 5)) for k in range(10): axes[0,k].set_axis_off() axes[0,k].imshow(train_x[k]) axes[1,k].set_axis_off() axes[1,k].imshow(train_y[k].squeeze())

Lançamos nossa rede. Deixe-me lembrá-lo de que é o mesmo para todas as opções.
input_layer = Input((w_size, w_size, 3)) output_layer = build_model(input_layer, 16) model = Model(input_layer, output_layer) model.compile(loss=bce_dice_loss, optimizer=Adam(lr=1e-3), metrics=[my_iou_metric]) model.load_weights('./keras.weights', by_name=False) while True: history = model.fit(train_x, train_y, batch_size=32, epochs=1, verbose=1, validation_split=0.1 ) if history.history['my_iou_metric'][0] > 0.75: break
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 56s 8ms/step - loss: 0.6815 - my_iou_metric: 0.2168 - val_loss: 0.2078 - val_my_iou_metric: 0.4983
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 53s 7ms/step - loss: 0.1470 - my_iou_metric: 0.6396 - val_loss: 0.1046 - val_my_iou_metric: 0.7784
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 53s 7ms/step - loss: 0.0642 - my_iou_metric: 0.8586 - val_loss: 0.0403 - val_my_iou_metric: 0.9354
A hipótese é confirmada, polígonos e elipses são facilmente distinguíveis. Um leitor atento notará aqui - é claro que são diferentes, uma pergunta sem sentido, qualquer IA normal pode distinguir uma curva da segunda ordem da linha da primeira. I.e. a rede determina facilmente a presença de um limite na forma de uma curva de segunda ordem. Não discutiremos, substitua o oval por um heptágono e verifique.
Quinta experiência, a mais difícil
Não há curvas, apenas faces lisas de heptágonos regulares inclinados e rotados e polígonos quadrangulares arbitrários. Introduzimos na função o gerador de imagens / máscaras - apenas projeções de heptágonos regulares e polígonos quadrangulares arbitrários da mesma cor.
revisão final da função de geração de imagem def next_pair(_n = 7): p = np.random.sample() - 0.5 c_x = np.random.sample()*(w_size-2*radius_max) + radius_max c_y = np.random.sample()*(w_size-2*radius_max) + radius_max radius = np.random.sample()*(radius_max-radius_min) + radius_min d = np.random.sample()*0.5 + 1 a_deg = np.random.sample()*360 a_rad = np.deg2rad(a_deg) poly = []
Como antes, criamos matrizes e analisamos os 10 primeiros.
máscaras de construção for k in range(train_num): img, msk = next_pair() train_x[k] = img train_y[k] = msk fig, axes = plt.subplots(2, 10, figsize=(20, 5)) for k in range(10): axes[0,k].set_axis_off() axes[0,k].imshow(train_x[k]) axes[1,k].set_axis_off() axes[1,k].imshow(train_y[k].squeeze())
input_layer = Input((w_size, w_size, 3)) output_layer = build_model(input_layer, 16) model = Model(input_layer, output_layer) model.compile(loss=dice_loss, optimizer=Adam(lr=1e-3), metrics=[my_iou_metric]) model.load_weights('./keras.weights', by_name=False) while True: history = model.fit(train_x, train_y, batch_size=32, epochs=1, verbose=1, validation_split=0.1 ) if history.history['my_iou_metric'][0] > 0.75: break
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 54s 7ms/step - loss: 0.5005 - my_iou_metric: 0.1296 - val_loss: 0.1692 - val_my_iou_metric: 0.3722
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 52s 7ms/step - loss: 0.1287 - my_iou_metric: 0.4522 - val_loss: 0.0449 - val_my_iou_metric: 0.6833
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 52s 7ms/step - loss: 0.0759 - my_iou_metric: 0.5985 - val_loss: 0.0397 - val_my_iou_metric: 0.7215
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 52s 7ms/step - loss: 0.0455 - my_iou_metric: 0.6936 - val_loss: 0.0297 - val_my_iou_metric: 0.7304
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 52s 7ms/step - loss: 0.0432 - my_iou_metric: 0.7053 - val_loss: 0.0215 - val_my_iou_metric: 0.7846
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 53s 7ms/step - loss: 0.0327 - my_iou_metric: 0.7417 - val_loss: 0.0171 - val_my_iou_metric: 0.7970
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 52s 7ms/step - loss: 0.0265 - my_iou_metric: 0.7679 - val_loss: 0.0138 - val_my_iou_metric: 0.8280Sumário
Como você pode ver, a rede distingue entre projeções de heptágonos regulares e polígonos quadrangulares arbitrários com uma precisão de 0,828 no conjunto de testes. O treinamento em rede é interrompido por um valor arbitrário de 0,75 e provavelmente a precisão deve ser muito melhor. Se prosseguirmos com a tese de que a rede encontra primitivas e suas combinações determinam o objeto, então, no nosso caso, existem duas áreas com uma média diferente do fundo, não há primitivas na compreensão do homem. Não há linhas óbvias de uma cor e não há cantos, respectivamente, apenas áreas com bordas muito semelhantes. Mesmo se você criar linhas, os dois objetos da imagem serão criados com as mesmas primitivas.
Uma pergunta para os conhecedores - o que a rede considera ser um sinal pelo qual distingue “barcos” de “interferência”? Obviamente, essa não é a cor ou a forma das bordas dos barcos. Obviamente, podemos continuar a estudar mais essa construção abstrata do "mar" / "navios", não somos a Academia de Ciências e podemos realizar pesquisas apenas por curiosidade. Podemos mudar os heptágonos para octógonos ou preencher a figura com ângulos regulares de cinco e seis e ver se a rede deles distingue ou não. Deixo isso para os leitores - embora também tenha me perguntado se a rede pode contar o número de cantos do polígono e, para o teste, organizar polígonos não regulares na imagem, mas suas projeções aleatórias.
Existem outras propriedades não menos interessantes de tais barcos, e esses experimentos são úteis, pois nós mesmos definimos todas as características probabilísticas do conjunto estudado e o comportamento inesperado de redes bem estudadas adicionará conhecimento e trará benefícios.
Fundo selecionado aleatoriamente, cor selecionada aleatoriamente, localização do barco / elipse selecionada aleatoriamente. Não há linhas nas fotos, há áreas com características diferentes, mas não há linhas monocromáticas! Nesse caso, é claro, existem simplificações e a tarefa pode ser ainda mais complicada - por exemplo, escolha cores como 0,0 ... 0,9 e 0,1 ... 1,0 - mas para a rede não há diferença. A rede pode e encontra padrões diferentes daqueles que uma pessoa vê e encontra claramente.
Se um dos leitores estiver interessado, você poderá continuar pesquisando e escolhendo nas redes, se o que não der certo ou não estiver claro, ou se um novo e bom pensamento aparecer e impressionar com sua beleza, você sempre poderá compartilhar conosco ou perguntar aos mestres (e também aos mestres) e peça ajuda qualificada na comunidade ODS.