Imagine: uma ligação às três da manhã, você atende e ouve um grito de que ninguém mais usa o seu produto. Assustador Na vida, é claro, não é assim, mas se você não prestar a devida atenção ao problema da saída de usuários, poderá se encontrar em uma situação semelhante.
Já descrevemos em detalhes o que é uma saída: nos aprofundamos na teoria e mostramos como transformar uma rede neural em um oráculo digital. Especialistas em Plarium Krasnodar conhecem outra maneira de prever. Nós vamos falar sobre ele.

Este não é o RFM que precisamos.
O RFM é um método usado para segmentar clientes e analisar seu comportamento. Com base nos dados obtidos, você pode criar um programa de fidelidade para cada grupo, criar uma distribuição de usuários e prever quando eles retornarão para compras.
A história do desenvolvimento da RFM começou em 1987, quando foi publicado o artigo
Contando seus clientes: quem são e o que farão a seguir . Descreveu um método de análise baseado na distribuição de Pareto (uma família de dois parâmetros de distribuições absolutamente contínuas).
O modelo foi chamado Pareto / NBD e levou em consideração apenas o histórico de compras dos usuários. Na interpretação clássica, o trabalho desse método foi construído em cinco pilares, ou aproximações:
- Enquanto os usuários estiverem ativos, o número de transações realizadas pelo comprador durante o período t obedece à distribuição de Pareto com um λt médio.
- A heterogeneidade do parâmetro λ (taxa de transação) segue uma distribuição gama com os parâmetros r e α.
- Cada comprador tem um período ilimitado de tempo "vida" τ. O ponto em que o usuário se torna inativo é distribuído exponencialmente com o parâmetro μ (taxa de abandono).
- A heterogeneidade do parâmetro μ entre os usuários segue uma distribuição gama com os parâmetros s (forma) e β (escala).
- Os parâmetros λ e μ podem variar independentemente entre os compradores.
As desvantagens deste modelo foram a alta complexidade do cálculo das funções hipergeométricas de Gauss e a busca pela função de máxima verossimilhança.
Em um artigo de 2003,
“Contando seus clientes”, a maneira fácil: uma alternativa ao modelo de Pareto / NBD , foi publicada a idéia de implementar um modelo melhor. Além do histórico de compras, foram utilizados mais dois parâmetros: frequência e prescrição. Sua principal diferença em relação a Pareto / NBD foi como é determinado o momento em que o cliente sai.
No cenário clássico, supunha-se que o usuário pudesse sair a qualquer momento, independentemente da frequência e padrão de suas compras no passado. A nova abordagem baseia-se na hipótese de que o comprador pode começar a perder o interesse imediatamente após a conclusão da transação.
Isso simplificou o cálculo e levou ao modelo beta-geométrico (BG / NBD). Ele usa três parâmetros principais: recência, frequência, monetário, - bem como quatro parâmetros adicionais: r, α, a, b (os parâmetros aeb foram adicionados a partir da
distribuição beta ).
O RFM ajuda a prever se um cliente fará uma compra no futuro. Os especialistas em Plarium Krasnodar modificaram esse método.
Preveja a saída de maneira simples e com bom gosto
Para cálculos, precisamos de uma matriz de dados sobre as sessões de jogos. É recalculado em uma matriz composta por parâmetros de RFM e em mais quatro coeficientes, selecionados pelo modelo no processo de aprendizado.
No contexto de um jogo, os parâmetros adquirem os seguintes significados:
- Rência - quanto tempo o usuário estava jogando no momento do último login;
- Frequência - com que frequência o usuário voltou a entrar no jogo;
- M onetário - há quanto tempo o usuário toca (tempo de "vida").
Os parâmetros são agregados em uma matriz. Em seguida, ele é carregado em um modelo que calcula a probabilidade de "vida" dos usuários - a chance de eles continuarem a jogar.
Os cálculos são feitos de acordo com a fórmula:
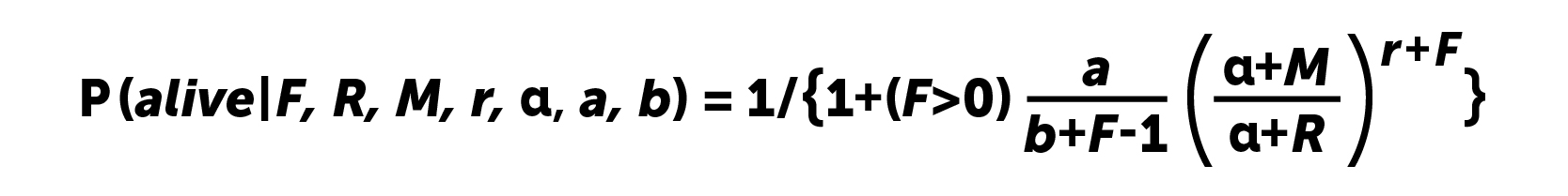
Obviamente, para usuários sem reentrada, a probabilidade de "vida" será uma. Em 2008, os autores do artigo
Computing P (live) Using the BG / NBD Model propuseram uma solução para esse problema. As empresas de jogos podem usar duas opções que dão resultados semelhantes.
Método 1 - parâmetro π é inserido para todos os usuários. Mostra quais jogadores são considerados inativos.
Método 2 - uma unidade é adicionada ao parâmetro Frequency. Essa medida evita a degeneração da fórmula em Frequency = 0, mas adiciona artificialmente mais uma entrada no jogo para cada usuário.
Como adaptar o método RFM para desenvolvedores de jogos
Suponha que tenhamos um novo usuário. Ele acabou de entrar no jogo. Parâmetro
F = 1 (ou 0, dependendo dos cálculos), já que a primeira entrada não é considerada e o jogador ainda não teve entradas repetidas.
O usuário joga três dias. Os parâmetros mudam:
F leva em consideração apenas as entradas diárias, portanto seu valor é 2 e os indicadores
M e
R são 3. Usando esses dados, obtemos a probabilidade de "vida" próxima à unidade.
No dia seguinte, o usuário não entra no jogo. O parâmetro
M é atualizado, enquanto
F e
R permanecem os mesmos. Substituindo todos os valores da fórmula, vemos que o indicador de probabilidade se tornou mais baixo.
Se o usuário não jogar durante a semana, o indicador
M é atualizado novamente e a probabilidade de "vida" cai ainda mais.
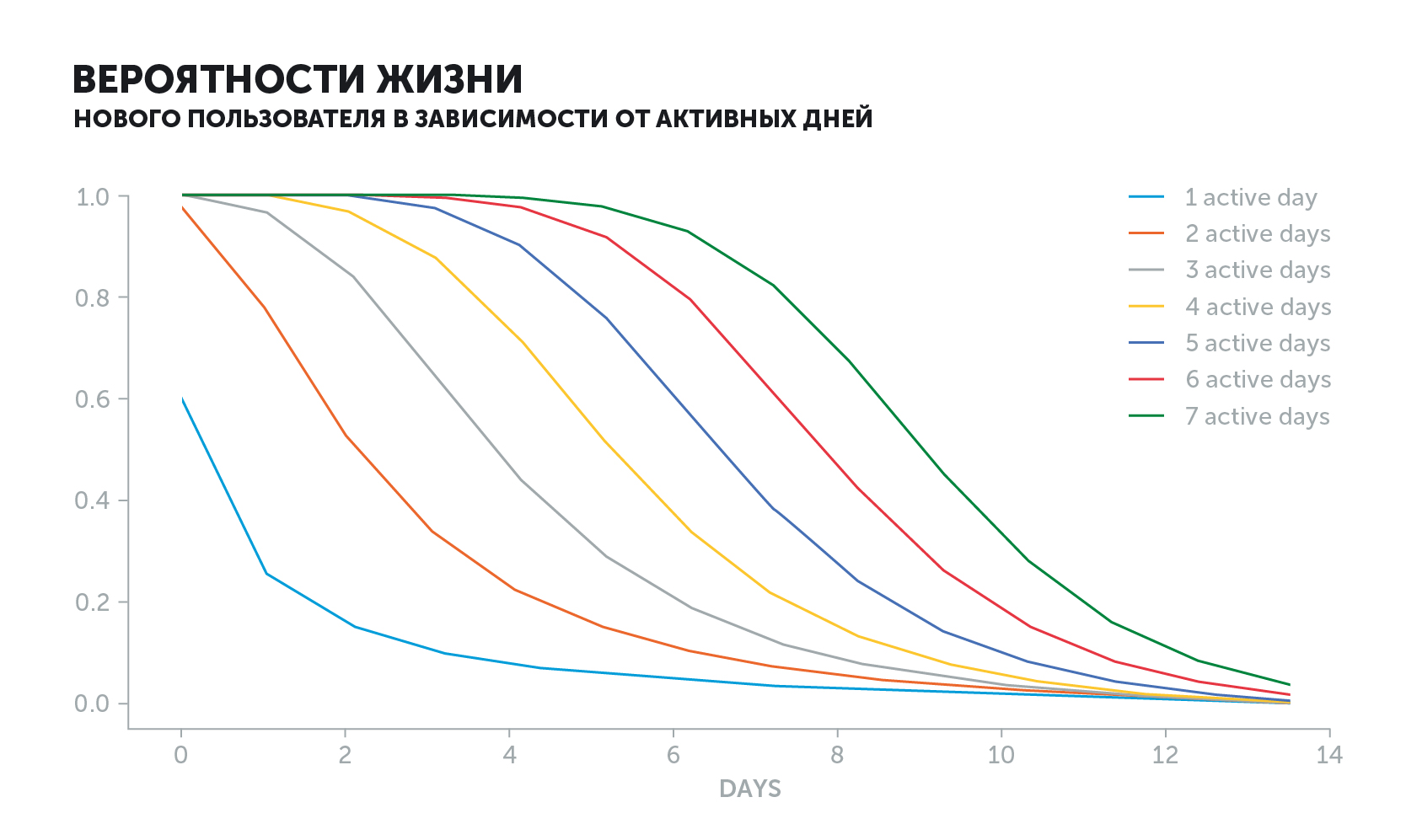
O gráfico do usuário ativo parece diferente. A probabilidade de uma "vida" diminuirá dependendo de sua história. Se ele entrou no jogo todos os dias e parou subitamente, o valor do indicador cairá muito mais rápido do que se ele jogasse a cada dois dias.

Prós e contras não óbvios do RFM
A principal vantagem desse método é sua simplicidade:
- para cálculos, você não precisa usar um aparato matemático complexo;
- os indicadores são calculados usando uma fórmula relativamente simples;
- Você pode ficar sem pipelines complexos para dados;
- todos os parâmetros ideais do modelo são selecionados automaticamente.
Além disso, os dados RFM são fáceis de interpretar. Estudando a história do usuário, pode-se entender por que ele tem essa probabilidade de "vida". Freqüentemente, ao trabalhar com métodos mais complexos, é mais difícil tirar conclusões específicas.
O RFM também tem desvantagens.
Em primeiro lugar , este não é o método mais preciso. Funciona bem, mas vários parâmetros não são usados nos cálculos. Por exemplo, muitos usuários que começam a perder o interesse por hábito entram no jogo. Ou seja, o número médio de sessões de jogos por dia diminui e a frequência de reentrâncias não muda.
Segundo , o método não leva em consideração a atividade do usuário: quantos recursos ele transferiu, se atacou o inimigo ou criou tropas. Se considerarmos todos os jogadores com uma probabilidade de "vida" igual a ~ 0,8, dependendo dos parâmetros e de sua história, além dos ativos, haverá aqueles que entrarão a cada três dias.
Em terceiro lugar , o usuário falecido fica "vivo" quando ele inicia o jogo novamente. O que ele tem que fazer isso um mês após o último login. Tais situações complicam a detecção de jogadores com grandes pausas entre as sessões. Em geral, isso não é crítico, embora introduza um certo desequilíbrio quando tentamos entender se o usuário está “vivo” ou não.
Não é melhor usar uma rede neural?
Melhor, mas antes de tudo, você precisa entender como implementar o projeto: resolver tarefas de larga escala rapidamente ou avançar gradualmente em direção à meta.
A análise RFM mostra a probabilidade de "vida" do usuário no momento em que o cálculo é feito. Não conseguiremos entender se o jogador sairá em duas ou três semanas e a rede neural poderá. Dada toda a infraestrutura, criar um sistema tão integrado para analisar o comportamento dos jogadores do zero é muito mais difícil. Além disso, você precisa de uma linha de base, com a qual possa comparar a qualidade da rede neural. Essa abordagem provavelmente resultará em perdas financeiras se você não calcular a força.
Nossa experiência mostra que tarefas globais precisam ser implementadas gradualmente. Criar um protótipo funcional não é difícil, mas coletar e processar dados, configurar e treinar uma rede neural é outra questão. Esses processos podem durar muito tempo, o que sempre falta.
Por isso, decidimos primeiro usar um modelo mais simples: realizamos pesquisas, identificamos os prós e contras e testamos no trabalho. Os resultados nos convieram. O RFM possui falhas, mas elas são compensadas generosamente pela facilidade de uso. E a rede neural é o próximo passo para melhorar o sistema.