As novas evidências, de autoria do escritor australiano de ficção científica Greg Egan, e a prova de 2011, publicada anonimamente online, foram reconhecidas como avanços significativos no estudo do mistério que os matemáticos pesquisam há 25 anos.

Em 16 de setembro de 2011, um fã de anime postou uma pergunta matemática de 4chan na série cult "The
Melancholy of Haruhi Suzumiya " no fórum. A primeira temporada do programa, onde houve viagens no tempo, foi exibida em uma ordem diferente da cronológica, e durante o programa e o lançamento subsequentes em DVD, a ordem dos episódios foi novamente alterada. Na Internet, os fãs discutiram em que ordem é melhor assistir a série e o autor da pergunta: se o público queria assistir à série em todas as ordens possíveis, quantos episódios estariam em sua lista mais curta? [
refere-se a uma lista na qual você pode encontrar qualquer sequência de episódios / aprox. perev. ]
Em menos de uma hora, um autor anônimo
respondeu à pergunta - não uma solução completa, mas um limite inferior ao número necessário de episódios. Pelo seu raciocínio, aplicável a qualquer número de episódios, seguiu-se que, para a primeira temporada de Haruhi, composta por 14 episódios, o público teria que assistir pelo menos 93.884.313.611 episódios seguidos para estudar todas as permutações possíveis. "Examine as evidências de falhas que eu poderia ter perdido", escreveu o autor da resposta.
Durante sete anos, a prova passou despercebida na comunidade matemática - e naquele momento apenas um matemático profissional o notou, e ele não a estudou completamente o suficiente. No entanto, de repente, no mês passado, o escritor australiano de ficção científica
Greg Egan provou um novo
limite superior no número de episódios necessários. A descoberta de Egan voltou a despertar interesse na tarefa e chamou a atenção para o recorde referente ao limite inferior de 2011. Agora, essas duas evidências são consideradas avanços significativos no estudo do mistério que os matemáticos pesquisam há pelo menos 25 anos.
Os matemáticos verificaram rapidamente o limite superior de Egan, que, como o limite inferior, é aplicável a seqüências de qualquer comprimento. Então, Robin Houston, um matemático em visualização de dados em Kiln, e
Jay Panton, da Marquette University em Milwaukee, confirmaram independentemente o trabalho de um autor anônimo da 4chan. "Muito esforço foi feito para verificar a validade dessa hipótese", disse Panton, já que as idéias principais da prova não foram expressas com clareza suficiente.
E agora, Houston e Panton, juntamente com
Vince Vater, da Universidade da Flórida, escreveram um
trabalho formal . Nele, eles indicaram o primeiro autor como "um pôster 4chan anônimo".
"O estranho é que essa prova muito elegante de um fato anteriormente desconhecido apareceu em um lugar tão improvável", disse Houston.
Cidades de permutações
Se a série tiver apenas três episódios, existem seis maneiras possíveis de assisti-los: 123, 132, 213, 231, 312 e 321. Eles podem ser colados e fazer uma lista de 18 episódios, incluindo cada versão do pedido. No entanto, também existe um método de colagem mais eficiente: 123121321. Essa sequência contendo todas as permutações de um conjunto de n caracteres é chamada super permutação.
Em 1993, Daniel Ashlock e Janet Tilotson descobriram que, ao estudar as super permutações mais curtas para vários valores de n, os fatoriais começam a aparecer rapidamente - os mesmos valores escritos na forma n!, Ou seja, multiplicando todos os números de 1 a n (por exemplo, 4 ! = 4 * 3 * 2 * 1).
Se houver apenas 1 episódio em sua série, a duração da super permutação mais curta será 1! (também conhecida como a boa e antiga unidade). Para uma série de dois episódios, a super permutação mais curta (121) tem uma duração de 2! + 1! .. Para três episódios (exemplo acima), a duração é 3! + 2! + 1!, E para quatro episódios (123412314231243121342132413214321) será 4! + 3! + 2! + 1! .. A regra fatorial tornou-se geralmente aceita (embora ninguém pudesse provar que isso é verdade para todos os n), e os matemáticos posteriores confirmaram isso para n = 5.
Então, em 2014, Houston impressionou os matemáticos,
mostrando que para n = 6 a regra parou de funcionar. A regra prevê que seriam necessários 873 episódios para assistir a seis episódios de todas as formas possíveis, mas Houston encontrou uma maneira de fazer isso em 872. E como existe uma maneira simples de transformar uma super permutação curta para n caracteres em uma super permutação curta para n + 1 caracteres, o exemplo de Houston significava que a regra fatoriais não funciona para todos n> 6.
A construção de Houston transforma a tarefa de super permutação no famoso problema dos vendedores ambulantes, que está procurando o caminho mais curto por várias cidades. Especificamente, super permutações estão associadas ao problema do vendedor “assimétrico”, no qual cada caminho entre duas cidades tem seu próprio preço (não necessariamente o mesmo em ambas as direções), e o objetivo é encontrar o caminho mais barato em todas as cidades.
Essa transformação é fácil de entender: imagine que cada permutação é uma cidade e imagine o caminho de cada permutação para qualquer outra permutação. No problema da super permutação, precisamos da menor seqüência de dígitos em que todas as permutações estejam presentes, de modo que nosso objetivo é passar por todas as permutações para adicionar o menor número possível à permutação inicial. Anunciamos que o custo de cada caminho é simplesmente o número de dígitos que precisamos anexar ao final da primeira permutação para obter o segundo. No exemplo com n = 3, o caminho de 231 a 312 custa $ 1, pois precisamos adicionar apenas 2 ao final de 231 para obter 312, e o caminho de 231 a 132 custa $ 2, pois precisamos adicionar 32. Nesta formulação, a maneira mais barata de todas as cidades correspondem diretamente à menor super permutação.
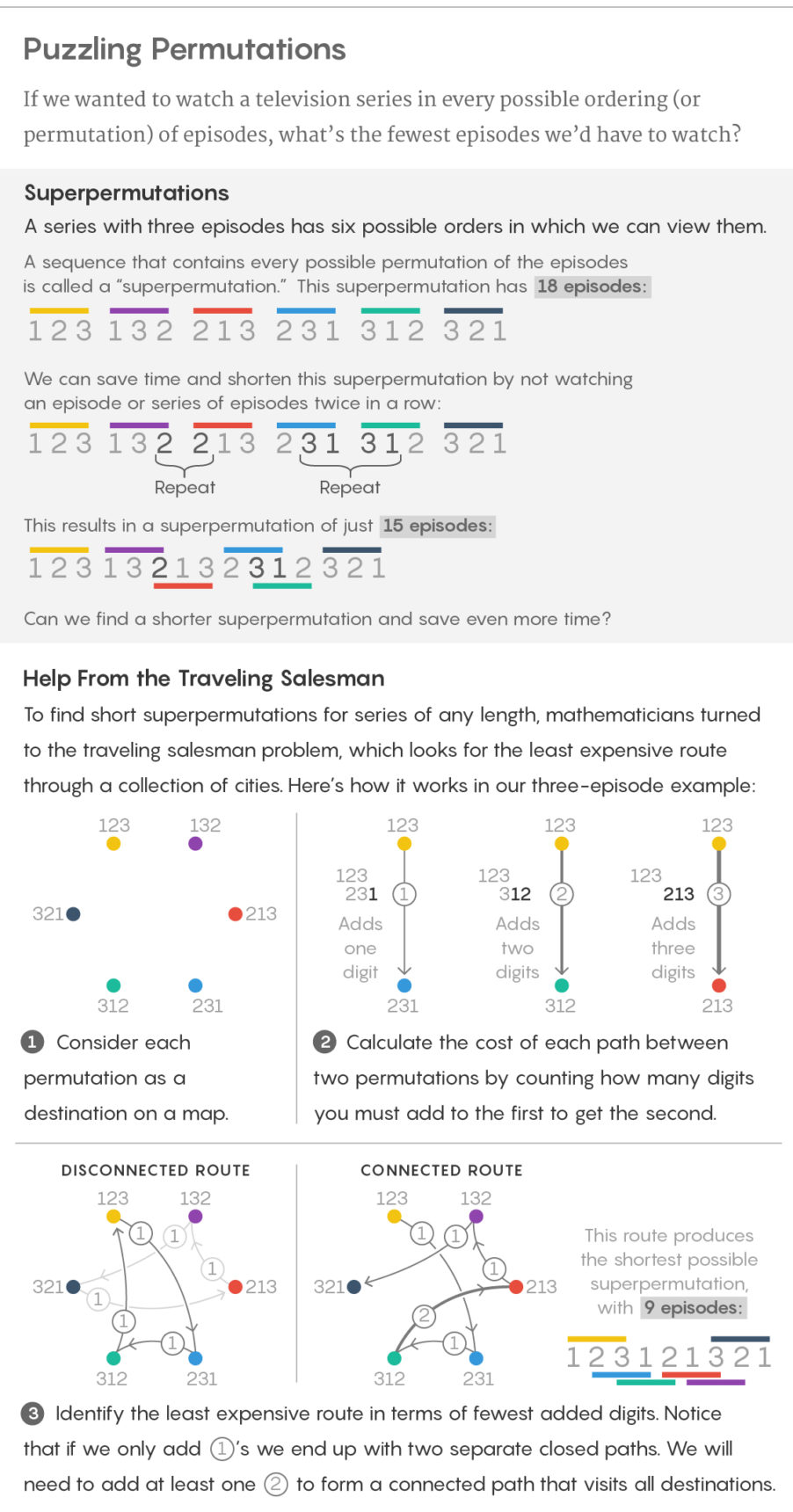
Essa transformação significou que Houston poderia direcionar todos os recursos dos algoritmos para resolver o problema do vendedor ambulante para o problema de super permutação. Esse problema é conhecido por pertencer à classe dos complexos NP, o que significa a ausência de um algoritmo eficaz que possa resolvê-lo no caso geral. No entanto, existem algoritmos que podem resolver efetivamente algumas variedades do problema e outros algoritmos podem produzir boas soluções aproximadas. Houston usou um destes últimos para emitir uma super permutação de 872 dígitos.
Como ele deu apenas uma solução aproximada, pode até não ser a super permutação mais ideal. Os matemáticos estão agora conduzindo uma volumosa pesquisa computacional pela menor permutação de 6 caracteres, disse Panton. "Sabemos que nossas pesquisas terminarão em um tempo finito, mas não sabemos se levará uma semana ou um milhão de anos", disse ele. "Não há barra de progresso."
Ordem errada
Quando o trabalho de Houston apareceu, um post anônimo no 4chan já estava em seu canto da Internet há quase três anos. Um matemático,
Nathaniel Johnston, da Mount Ellison University, notou uma cópia desta postagem em outro site alguns dias após a publicação dela - e não porque ele era um amante de anime, mas porque ele inseriu vários pedidos no Google, associado a super permutações.
Johnston leu as evidências e isso lhe parecia confiável, mas ele não desperdiçou sua energia em um exame completo. Naquela época, os matemáticos acreditavam que a fórmula fatorial para super permutações provavelmente estava correta e, quando você acha que sabe a resposta exata para a pergunta, não está interessado no limite inferior da estimativa. Em outras palavras, os episódios da série sobre super permutações foram na ordem errada.
Depois disso, Johnston mencionou o limite inferior em um
par de sites , mas "acho que ninguém prestou atenção especial a isso", disse ele.
Então, em 26 de setembro de 2018, o matemático
John Baez, da Universidade da Califórnia em Riverside, twittou um
post sobre a descoberta de Houston em 2014, como parte de uma série de tweets sobre padrões matemáticos óbvios que param de funcionar.
Nota perev.: não havia uma série tão grande de tweets, apenas três. Os outros dois também são interessantes por si só, embora não estejam relacionados a este artigo. Diz-se que 6 é a distância mais popular entre dois primos adjacentes para todos os primos menores que 17.427.000.000.000.000.000.000.000.000.000.000 E, então, esse padrão de repente pára de funcionar! O segundo demonstra a seguinte conexão de integrais, funções trigonométricas e o número π

Mas apenas para n <9,8 × 10 42 !Seu tweet chamou a atenção de Egan, que estudou matemática há várias décadas, antes de sua carreira como escritor de ficção científica reconhecido (sua primeira história de sucesso, por uma sorte, foi chamada de "A Cidade das Permutações"). "Nunca deixei de me interessar por matemática", escreveu Egan pelo correio.
Egan se perguntou se era possível criar uma super permutação ainda mais curta que a de Houston. Ele mergulhou no estudo da literatura sobre como criar atalhos em redes de permutações e depois de algumas semanas encontrou o que precisava. Em alguns dias, ele deduziu um novo limite superior no comprimento da super permutação mais curta de n caracteres: n! + (n - 1)! + (n - 2)! + (n - 3)! + n - 3. É semelhante à fórmula fatorial, da qual muitos membros foram excluídos.
"Ele quebrou completamente o limite superior anterior", disse Houston.
O limite inferior do autor da postagem no 4chan estava sedutoramente próximo ao novo limite superior: n! + (n - 1)! + (n - 2)! + n - 3. Após a publicação do resultado, Egan Johnston lembrou os matemáticos da prova de um autor anônimo, e Houston e Panton logo provaram sua exatidão. Como no trabalho de Houston, os novos limites inferior e superior são adequados para super permutações do ponto de vista do problema do vendedor ambulante: o limite inferior mostra que o caminho por todas as cidades deve passar por um número mínimo de caminhos no valor de mais de US $ 1, e o limite superior cria um caminho especial para cada n, usando apenas compostos no valor de $ 1 e $ 2.
Agora, os pesquisadores estão tentando reunir os limites superior e inferior e encontrar uma fórmula única que resolva o problema da super permutação. "Provavelmente, no final, as pessoas ainda resolverão esse enigma", previu Baez. "Agora tudo parece bom."
Para os fãs de Haruhi, a solução de Egan fornece instruções precisas sobre como visualizar todas as opções possíveis para a primeira temporada, usando um total de 93.924.230.411. Você pode começar a assistir hoje ou pode esperar até que os matemáticos possam reduzir esse número. O limite inferior de um autor anônimo prova que esse corte não os salvará em mais de 40 milhões de episódios - no entanto, isso é suficiente para começar a se preparar para a segunda temporada.