Acelerômetros e giroscópios MEMS - Compreendendo as especificações

"Houston, temos problemas", veio uma voz cansada em meu cérebro, tentando passar pela folha de dados do InvenSense IMU MPU-9250 à noite. Quando todas as palavras individualmente são compreensíveis, mas seu relacionamento é confundido com impossibilidade. Tudo começou com o parâmetro LSB, sobre o qual eu apenas me lembrava vagamente que na tradução era o Menos Significativo. Depois, foram “Resolução”, “Sensibilidade”, e ainda mais percebi que o texto resultante já pode ser intitulado “Folha de dados para manequins”.

Um pouco sobre os principais blocos do módulo inercial.

Giroscópio MEMS

O MPU-9250 consiste em três sensores independentes de velocidade angular vibracional uniaxial (giroscópios MEMS) que respondem à rotação em torno dos eixos X, Y, Z. Duas massas suspensas oscilam em eixos opostos. Com o advento da velocidade angular, o efeito Coriolis causa uma mudança na direção da vibração ( $$$\ vec {F} _K = -2m [\ vec {\ omega} \ times \ vec {v} _r]$ que é fixado por um sensor capacitivo. O componente capacitivo diferencial medido é proporcional ao ângulo de movimento [Tempo da Eletrônica]. O sinal resultante é amplificado, desmodulado e filtrado, resultando em uma tensão proporcional à velocidade angular de rotação. Este sinal é digitalizado usando o ADC de 16 bits integrado. A taxa de amostragem pode variar programaticamente de 3,9 a 8000 amostras por segundo (amostras por segundo, SPS), e os filtros passa-baixo definidos pelo usuário (LPF) fornecem uma ampla variedade de possíveis frequências de corte. O filtro passa-baixas é necessário, em particular, para remover vibrações dos motores (como regra, acima de 20-25 Hz).

Acelerômetro MEMS de três eixos

Usa uma massa de teste separada para cada eixo, que muda quando a aceleração ocorre ao longo desse eixo (fixada por sensores capacitivos). A arquitetura MPU-9250 reduz a exposição a variações de temperatura e variações nos parâmetros elétricos. Quando o dispositivo estiver localizado em uma superfície plana, ele medirá 0g nos eixos X e Y e + 1g no eixo Z. O fator de escala ( fator de escala - a razão entre a mudança no sinal de saída e a mudança no sinal medido de saída) é calibrado na fábrica e não depende da tensão de alimentação. Cada sensor é equipado com um ADC sigma-delta individual (consiste em um modulador e um filtro passa-baixo digital, mais sobre o dispositivo em [Easyelectronics]), cuja saída digital possui uma faixa de medição ajustável.

E quase o magnetômetro MEMS de três eixos

Baseado na tecnologia de efeito Hall de alta precisão. Inclui sensores magnéticos que determinam a força do campo magnético da terra ao longo dos eixos, um circuito de controle, um circuito de amplificação de sinal e um circuito computacional para processar sinais de cada sensor. Cada ADC possui uma resolução de 16 bits, uma faixa de medição $$$\ pm 4800 \ mu T$ . Para medir campos magnéticos fracos, é usada uma unidade no sistema SI de microtesley (μT) ou gauss (sistema G, GHS): $$$1 G. = 100 \ mu T$ , [Radio Pilot]).

Então, o que é LSB e como calculá-lo? Instrução de produção

Digamos que nosso acelerômetro agora esteja operando na faixa de medição $$$FS = \ pm 2g$ ou seja, toda a gama de valores possíveis será $$$2 \ cdot FS = 4g$ . Os valores de tensão correspondentes são digitalizados por um ADC de 16 bits, que pode dividir o intervalo inteiro o máximo possível $$$2 ^ {16} = 65536$ etapas. O incremento mínimo que pode ser detectado é apenas uma etapa $$$LSB = 2 \ cdot FS / 65536$ . Aqui devemos lembrar que a conta é conduzida do zero, para que, de fato, o valor máximo medido seja $$$2 \ cdot FS_ {true} = (2 ^ {16} - 1) * LSB = 65535 * LSB = 2 \ cdot FS - LSB$ . Ou seja, quanto mais bits em uma palavra digital ADC ou DAC, menor a discrepância. Nesse caso, a sensibilidade (às vezes chamada de fator de escala, fator de escala de sensibilidade) do sensor em uma faixa específica será determinada como a razão do sinal de saída elétrico e o impacto mecânico. Tradicionalmente indicado para uma frequência de sinal de 100 Hz e temperatura $$$T = + 25 ^ {\ circ} C.$ Para o MPU-9250, a sensibilidade é $$$2 ^ {16} / (2 \ cdot FS)$ etapas para cada g ou $$$^ {\ circ} / s$ ( $$$LSB / g$ , $$$LSB / (^ {\ circ} / s)$ ), para outra IMU, BMI088 da Bosch Sensortec, a sensibilidade do giroscópio é calculada da mesma maneira e para o acelerômetro é usada $$$(2 ^ {16} -2 ^ 4) / (2 \ cdot FS)$ etapas para cada g.



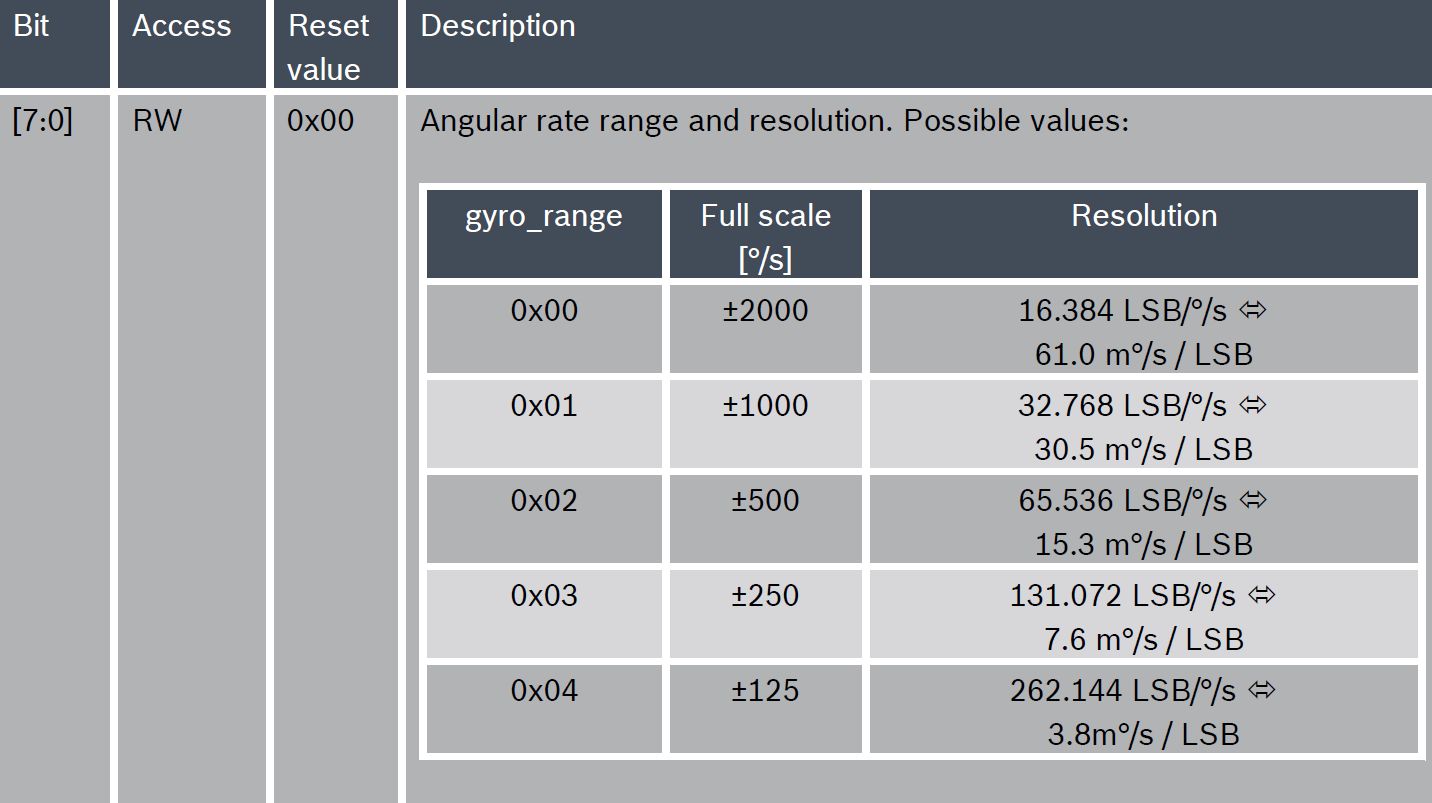
Retiramos as variantes FS da especificação para giroscópios e, para não levantarmos duas vezes, acelerômetros.





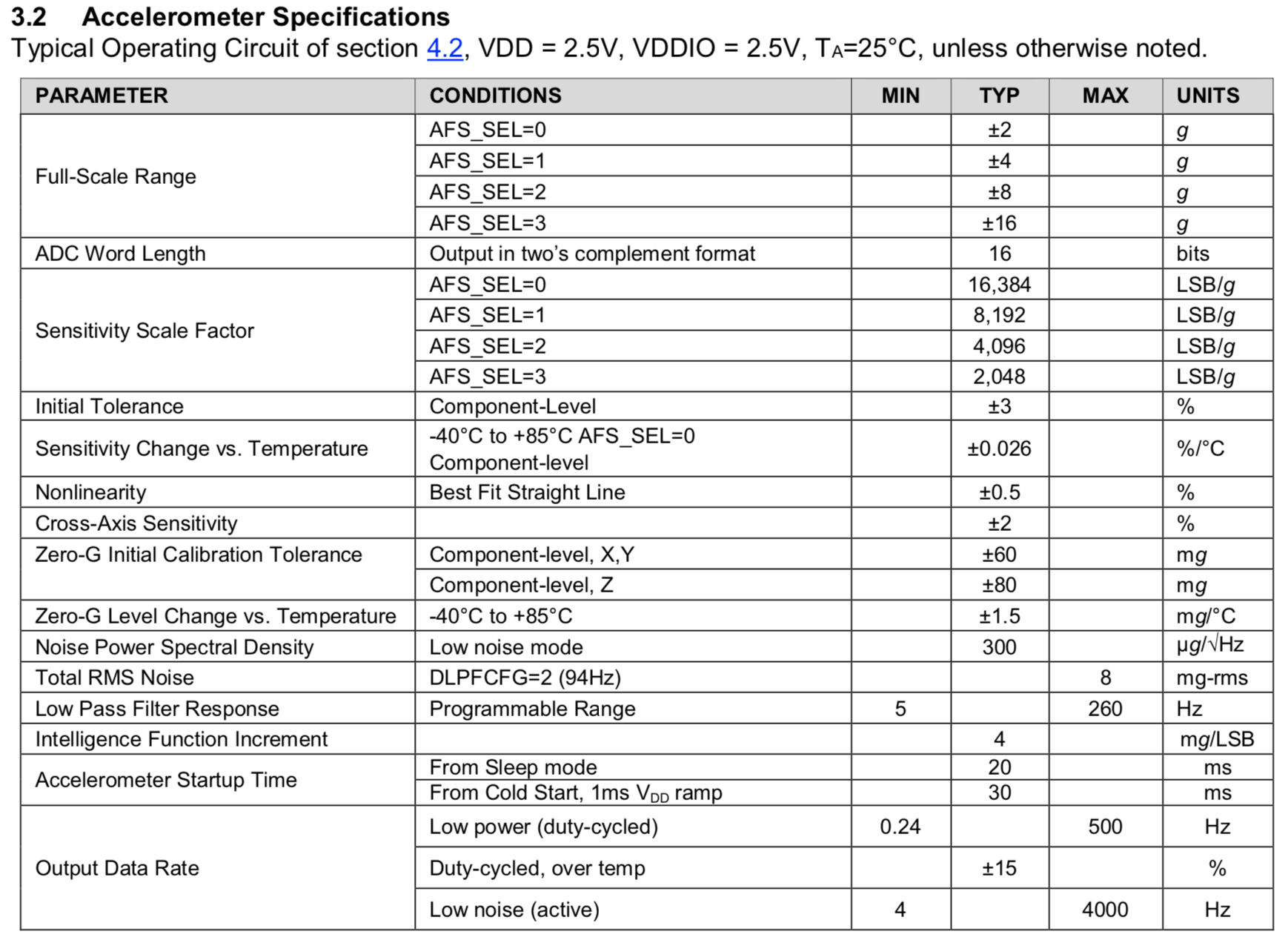
Também peguei o FS para acelerômetros na documentação do BMI088 (veja abaixo).

Giroscópio, 16 bits $$$(2 ^ N = 65535)$		Acelerômetro, 16 bits $$$(2 ^ N = 65535)$
Intervalo (FS) $$$^ {\ circ} / s$ (dps)	LSB, $$$^ {\ circ} / s$ (dps)	Faixa (FS), g	Mg de LSB
$$$\ pm 125$ (FS = 250)	0,004	$$$\ pm 2$ (FS = 4)	0,06
$$ (FS = 500)	0,008	$$$\ pm 3$ (FS = 6)	0,09
$$ (FS = 1000)	0,0015	$$$\ pm 4$ (FS = 8)	0,12
$$$\ pm 1000$ (FS = 2000)	0,03	$$$\ pm 6$ (FS = 12)	0,18
$$$\ pm 2000$ (FS = 4000)	0,06	$$$\ pm 8$ (FS = 16)	0,24
		$$$\ pm 12$ (FS = 24)	0,37
		$$ (FS = 32)	0,48
		$$$\ pm 24$ (FS = 48)	0,73

Parece que tudo se encaixou, você pode seguir em frente. Em alguns casos (abaixo, por exemplo, um recorte da documentação do BMI088), um parâmetro como a resolução é indicado separadamente.

De fato, parece que deveria ser um LSB. Mas por que vemos um valor em vez de vários vinculados a intervalos específicos? Eu tive que expandir a lista de fontes estudadas em busca de respostas.

O que é resolução?

O valor mínimo que o sensor vê com confiabilidade é extremamente importante ao tentar encontrar um equilíbrio entre preço e desempenho. Isso não é precisão - um sensor de alta resolução pode não ser particularmente preciso, assim como um sensor de baixa resolução em certas áreas pode ter precisão suficiente. Infelizmente, o LSB define apenas o valor mínimo teórico distinguível, desde que possamos usar todos os 16 bits do ADC. Esta é uma resolução no mundo digital. Em analógico, alguns dos passos serão barulhentos e o número de bits efetivos será menor.

Quais são as características do ruído e de onde elas vêm?

As fontes de ruído geralmente podem ser divididas em ruído eletrônico de um circuito que converte movimento em um sinal de tensão (ruído térmico Johnson, ruído de tiro, ruído rosa 1 / f de cintilação, etc.) e mecânico-mecânico (browniano devido à presença de pequenas partes móveis) do próprio sensor. As características deste último dependerão da frequência ressonante da parte mecânica do sistema $$$f_0$ (frequência de oscilação natural do sensor $$$\ omega_0 = 2 \ pi / f_0$ )

Ruído RMS em toda a faixa espectral - RMS total (quadrado médio da raiz)

Os níveis de ruído podem ser determinados de várias maneiras. Você pode considerá-los no domínio do tempo ou da frequência (após a transformação de Fourier). No primeiro caso, o ruído residual é considerado como o valor eficaz dos sinais do sensor fixo (na verdade, esse é o desvio padrão para amostragem em $$$\ overline x = 0$ ) por um certo período de tempo:

$$

$$x_ {RMS} = \ sigma_X = \ sqrt {\ sum_ {i = 1} ^ n {(x_i - \ overline x)} ^ 2 \ over {n-1}}$$

Acelerações ou velocidades de rotação angulares inferiores ao nível de ruído de banda larga serão indistinguíveis - esta é a resolução real. O valor eficaz de uma tensão ou corrente alternada (geralmente chamado de ativo ou efetivo) é igual ao valor de um sinal constante cuja ação executará o mesmo trabalho em uma carga ativa (resistiva) durante o período. Essa abordagem é mais eficaz na avaliação do ruído de banda larga, onde o ruído branco domina.

Para ruído branco, a relação de amplitude (valor instantâneo de pico) / rms com uma probabilidade de 99,9% é $$$N_ {PP} / N_ {RMS} = 6,6.$ Essa relação é chamada de fator cruzado (fator de crista, razão cruzada). Você pode escolher uma probabilidade de 95,5% - o fator cruzado será 4.



De fato, os sinais de ruído não se comportam tão bem e podem produzir picos que aumentam o fator cruzado em até 10 vezes. Em algumas especificações, você pode encontrar os valores $$$N_ {PP}$ ou o próprio multiplicador.

Em uma banda estreita de baixa frequência de 0,1 a 10 Hz, o papel principal é desempenhado pelo ruído de cintilação "1 / f", que é estimado usando a amplitude do sinal de ruído pico a pico.

Densidade espectral

Às vezes, é mais conveniente considerar um sinal no domínio da frequência, onde sua descrição é chamada espectro (a dependência da amplitude e da fase da frequência). Uma das possíveis características do ruído nas especificações é denominada densidade espectral de ruído (PSD), densidade espectral de ruído, densidade de potência de ruído ou simplesmente densidade de ruído ). Descreve a distribuição da potência do ruído em uma faixa de frequência. Independentemente da representação do sinal elétrico através de corrente ou tensão, a potência instantânea dissipada na carga pode ser normalizada (R = 1 Ohm) e expressa como $$$p (t) = {\ nu} ^ 2 (t) / R = i ^ 2 (t) R = x ^ 2 (t).$ Potência média dissipada pelo sinal durante um período de tempo $$$(- T / 2, T / 2),$

$$

$$P_x ^ T = \ frac {1} {T} \ int ^ {T / 2} _ {- T / 2} x ^ 2 (t) \, dt.$$

Potência é a taxa de entrada de energia. Sinais determinados e não periódicos são determinados por energia. Sinais periódicos e aleatórios são expressos em termos de potência, uma vez que não são limitados no tempo e, consequentemente, em energia, e a qualquer momento sua potência média é diferente de zero

$$

$$P_x = \ lim_ {T \ to \ infty} \ frac {1} {T} \ int ^ {T / 2} _ {- T / 2} x ^ 2 (t) \, dt.$$

Você pode lembrar [Sklyar] que um sinal periódico arbitrário é expresso por meio da combinação de um número infinito de harmônicas com frequências crescentes:

$$

$$x (\ lambda) = \ frac {a_0} {2} + \ sum_ {n = 1} ^ {\ infty} (a_n \ cos n \ lambda + b_n \ sin n \ lambda),$$

que depois de representar o cosseno e o seno na forma exponencial

$$

$$\ cos \ lambda = \ frac {e ^ {i \ lambda} + e ^ {- i \ lambda}} {2}, \ sin \ lambda = \ frac {e ^ {i \ lambda} - e ^ {- i \ lambda}} {2i}$$

e substituições $$$\ lambda = \ ômega t = 2 \ pi f_0 t = \ frac {2 \ pi t} {T_0}$ pode ser escrito como

$$

$$x (t) = \ frac {a_0} {2} + \ frac {1} {2} \ sum_ {n = 1} ^ {\ infty} [(a_n - ib_n) e ^ {em \ omega t} + (a_n + ib_n) e ^ {- in \ omega t}] = \ sum_ {n = - \ infty} ^ {\ infty} c_n e ^ {em \ omega t},$$

onde estão os coeficientes complexos (componentes espectrais) da série de Fourier para $$$x (t)$ ,

$$exibição $$ $$ \ begin {equação} c_n = \ frac {1} {T_0} \ int ^ {T_0 / 2} _ {- - T_0 / 2} x (t) e ^ {- em \ ômega t}, dt = \ begin {cases} \ frac {1} {2} (a_n-ib_n), & n> 0 \\ \ frac {a_0} {2}, & n = 0 \\ \ frac {1} {2} ( a_n + ib_n), & n <0 \ end {cases} \ end {equação} $$ exibem $$

No caso geral, esses coeficientes são representáveis ​​da seguinte maneira:

$$

$$c_n = | c_n | e ^ {i \ theta_n},$$

$$

$$| c_n | = \ frac {1} {2} \ sqrt {a_n ^ 2 + b_n ^ 2}, \ theta_n = \ arctan \ left (\ frac {b_n} {a_n} \ right), b_0 = 0, c_0 = \ frac {a_0} {2}.$$

Amplitude e espectro de fase são chamados de gráficos de dependência. $$$| c_n |$ e $$$\ theta_n$ da frequência. Densidade espectral de potência $$$PSD (f)$ sinal periódico $$$x (t)$ fornece a distribuição da potência do sinal em uma faixa de frequência:

$$

$$PSD (f) = \ soma ^ {\ infty} _ {n = - \ infty} | c_n | ^ 2 \ delta (f-nf_0)$$

e tem dimensão $$$[W / Hz] = [x ^ 2 / Hz].$ A potência normalizada média do sinal real será

$$

$$P_x = \ int ^ {\ infty} _ {- \ infty} PSD (f), df.$$

Sinais aleatórios não periódicos (em particular, ruído) podem ser descritos como periódicos no sentido limitante. Se $$$T_0$ tende ao infinito, a sequência de impulsos se transforma em um impulso separado $$$x (t)$ , o número de linhas espectrais tende ao infinito, o gráfico de espectro se transforma em um espectro de frequência suave $$$X (f).$ Para este caso limitante, podemos determinar um par de transformadas integrais de Fourier

$$

$$X (f) = \ int ^ {\ infty} _ {- \ infty} x (t) e ^ {- i 2 \ pi f t}, dt$$

e

$$

$$x (t) = \ int ^ {\ infty} _ {- \ infty} X (f) e ^ {i 2 \ pi f t}, df,$$

onde $$$X (f)$ - imagem de Fourier.

A densidade espectral de potência de um sinal aleatório é determinada através do limite

$$

$$PSD (f) = \ lim_ {T \ to \ infty} \ frac {1} {T} | X_T (f) | ^ 2.$$

e descreve a distribuição da potência do sinal na faixa de frequência.

Como assumimos que a média do ruído branco dos sensores em estado estacionário é zero ( $$$\ overline x = \ overline x ^ 2 = 0$ ), o quadrado do valor eficaz é igual à variação e representa a potência total na carga normalizada:

$$

$$Noise_ {RMS} ^ 2 = \ sigma_x ^ 2 = P_x = \ int ^ {\ infty} _0 PSD (f), df = \ int ^ {Largura de banda} _0 PSD (f), df = PSD (Badnwidth - 0)$$

$$

$$RMS de ruído = \ sqrt {Densidade de ruído \ vezes a largura de banda}$$

Examinamos a especificação - ali, de fato, a raiz quadrada dela com a dimensão correspondente é indicada sob o nome de densidade espectral $$$[^ {\ circ} / s / \ sqrt {Hz}]$ ou $$$[\ mu g / \ sqrt {Hz}].$ Ou seja, o valor do ruído RMS sem indicar a banda de frequência na qual foi lido (largura de banda) não faz sentido.

Um pouco mais sobre a escolha da largura de banda

Na saída do sensor MEMS, obtemos sinais de diferentes frequências. Supõe-se que tenhamos uma certa idéia dos processos que estamos medindo antecipadamente. Por exemplo, ao determinar o vetor de aceleração de um drone, o ruído é a vibração do dispositivo. Você pode separá-los do sinal útil usando um filtro passa-baixo que corta todas as frequências acima da especificada (por exemplo, 200 Hz). O MPU-9250 oferece a capacidade de ajustar a frequência de corte do filtro passa-baixo usando o parâmetro com o nome mágico DLPFCFG . Significa Digital Low Pass Filter Configuration. Além disso, nas especificações, expressões menos misteriosas do tipo (DLPFCFG = 2, 92Hz) surgiram aqui e ali, mas para decodificar tive que entrar em outro documento, “Register Map and Descriptions”. Ele mostra quais conjuntos de bits nos quais os registros devem ser gravados para alcançar os efeitos desejados:



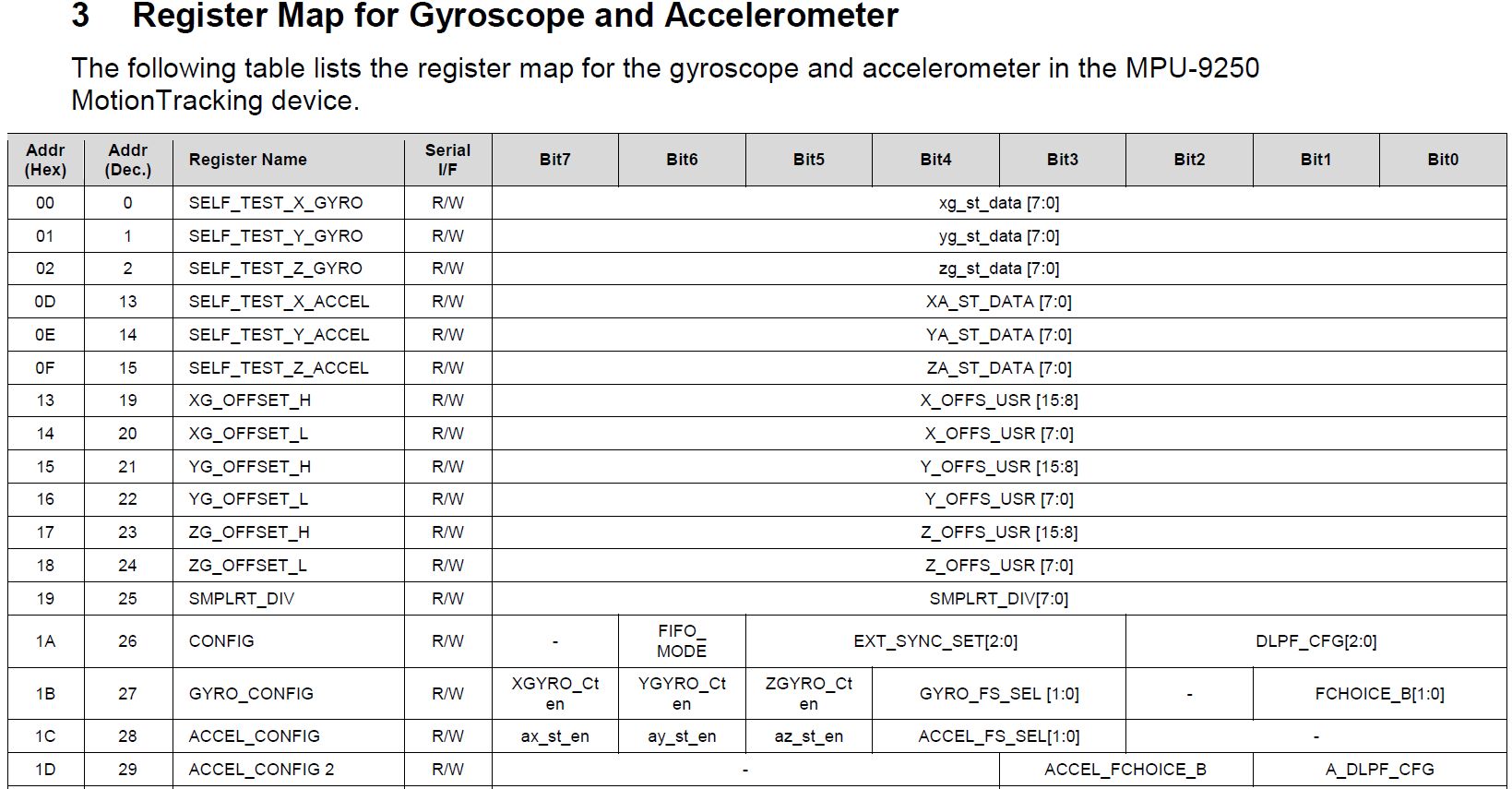
Omitindo os detalhes técnicos da configuração, pode-se dizer o seguinte. Nesse sensor, é realizada a filtragem personalizável das leituras, não apenas dos acelerômetros, giroscópios, mas também do sensor de temperatura. Para cada um, há um total de 7 a 10 modos, caracterizados por conceitos como largura de banda (Hz), atraso em ms, frequência de amostragem (Fs) em kHz.



A coluna “Densidade de ruído” em $$$\ mu g / rtHz = \ mu g / \ sqrt {Hz}$ , e a coluna "Largura de banda" foi complementada com o valor "3dB".



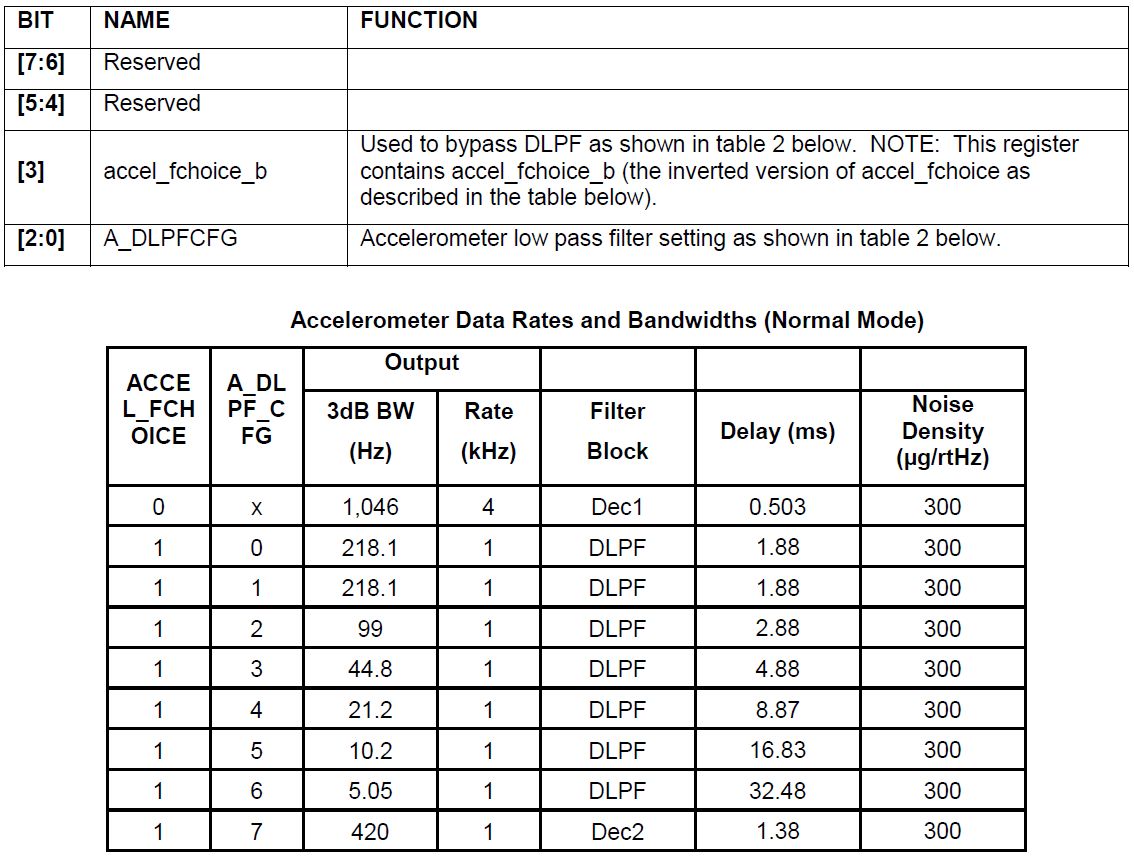
Não é mais fácil, então vamos direto à lista.

Legado da Roma antiga

Taxa de amostragem + dizimação $$$\ Delta \ Sigma$ ADC = taxa de dados de saída digital (ODR)

Com a frequência de amostragem (é a frequência de amostragem), tudo fica claro - este é o número de pontos de um sinal de tempo contínuo recebido por segundo durante a amostragem pelo ADC. Medido em hertz.

$$

$$Fs = \ frac {1} {\ delta t}$$

Para obter um valor próximo da amplitude de pico do sinal, é importante ter uma frequência de amostragem de pelo menos 10 vezes a frequência do sinal útil. O MPU-9250 oferece três opções: Fs = 32kHz, 8kHz, 1kHz.

Mas isso absolutamente não significa que o sinal na saída do acelerômetro ou giroscópio apareça com o mesmo período.

Se você usar os mesmos drones, tudo depende da luta para reduzir o consumo de energia, aumentar a velocidade dos cálculos e reduzir o ruído dos dados de saída. Você pode reduzir a frequência da atualização dos dados de saída, permitindo que algoritmos internos integrem informações de entrada por um período de tempo. O valor do RMS diminuirá, mas a largura de banda também diminuirá (o sensor pode detectar apenas os processos cuja frequência será inferior a 50% da taxa de atualização de dados).

Aqui é melhor lembrar o teorema de Kotelnikov imediatamente. Ela promete que, ao amostrar um sinal analógico, a perda de informações pode ser evitada (isto é, para restaurar o sinal sem distorção) se a frequência do sinal útil não exceder a metade da frequência de amostragem, também chamada de frequência de Nyquist . Na prática, um filtro anti-aliasing clássico (um filtro passa-baixo que reduz a contribuição dos componentes de frequência secundária no sinal de saída para níveis desprezíveis - GOST R 8.714-2010) requer na maioria dos casos uma diferença de pelo menos 2,5 vezes [Siemens].

Para Fs = 32kHz, a frequência Nyquist será 16kHz. Ao mesmo tempo, é improvável que um sinal útil ultrapasse a faixa fa = 20Hz (poucos podem mudar a direção do movimento mais de 20 vezes por segundo). No total, a frequência de amostragem é significativamente maior que a freqüência necessária para armazenar as informações contidas na banda fa (40Hz, 400 vezes maior), ou seja, o sinal útil é super amostrado. A banda entre as frequências fa e fs-fa não contém nenhuma informação útil. Você pode reduzir a taxa de amostragem (no diagrama, isso foi feito com o coeficiente M, [7]), afinando a sequência de amostras (amostras). Esse processo é chamado de dizimação .



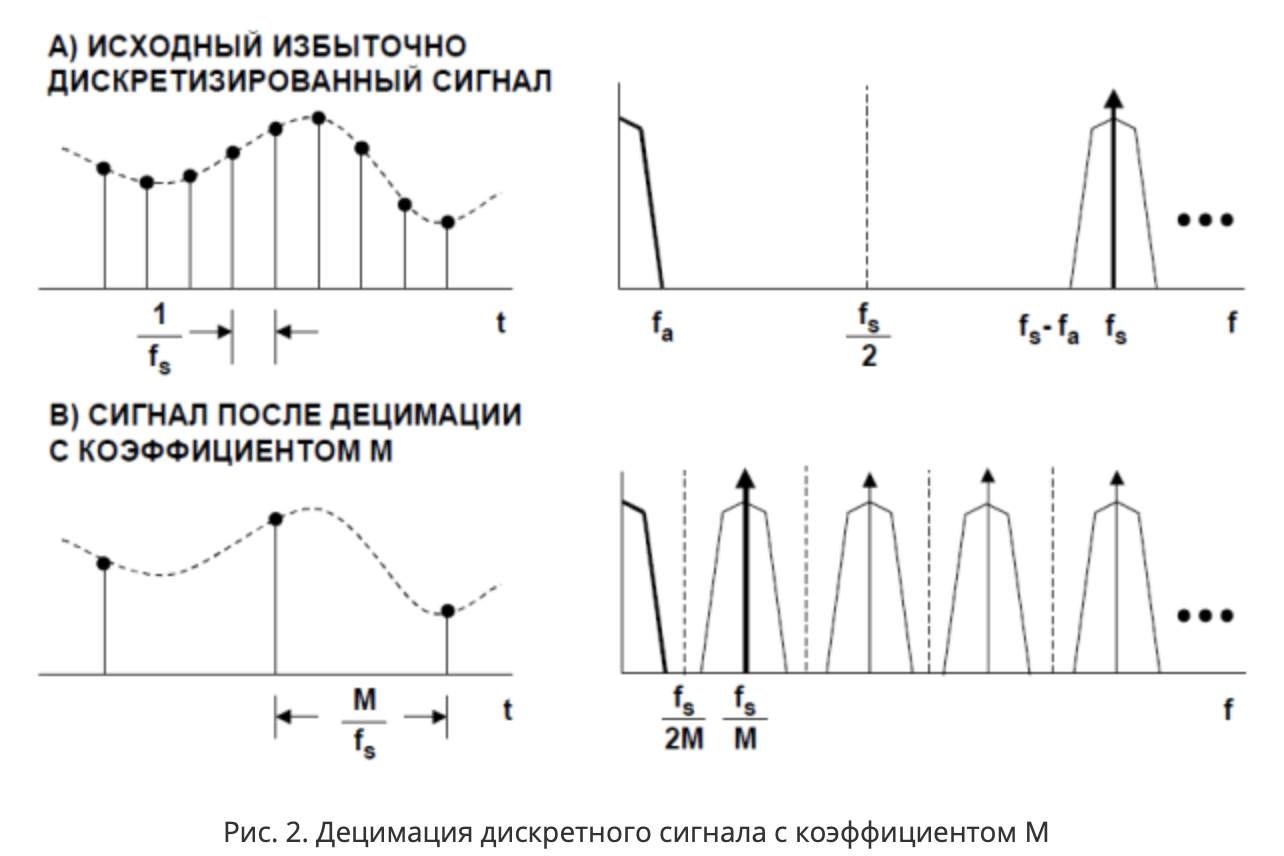
De acordo com a especificação no MPU-9250, os acelerômetros são equipados com um ADC sigma-delta . Esquemas baseados nele consomem energia mínima. Deve-se notar que a largura de banda desses conversores é muito estreita, não excede a faixa de som [Easyelectronics], mas para um quadrocóptero padrão, mais não é necessário. Eles consistem em dois blocos: $$$\ Sigma \ Delta$ -modulador e filtro passa-baixo de dizimação digital.

Por que combinar filtro passa-baixo e dizimação?

Trecho honesto da Wiki:

Se o sinal original não contém frequências mais altas que a frequência Nyquist do sinal dizimado, então a forma do espectro do sinal recebido (dizimado) coincide com a parte de baixa frequência do espectro do sinal original. A taxa de amostragem correspondente à nova sequência de amostragem é N vezes menor que a frequência de amostragem do sinal original.
Se o sinal original contiver frequências mais altas que a frequência Nyquist do sinal dizimado, a dizimação resultará em alias (superposição de espectros).

Assim, para preservar o espectro, é necessário, antes da dizimação, remover das frequências de sinal originais que são mais altas que a frequência Nyquist do sinal dizimado. A especificação MPU-9250 não contém muita informação sobre as características do DLPF, mas pesquisas de entusiastas podem ser encontradas [9].

Largura de banda, é resposta em frequência (resposta em frequência)

a faixa de frequência na qual o sensor detecta movimento e fornece um sinal de saída válido. Em algumas especificações, é dada a resposta de freqüência do sensor - a dependência da saída elétrica do acelerômetro em relação a tensões mecânicas externas com amplitude fixa, mas frequências diferentes. Dentro da largura de banda, a irregularidade da resposta em frequência não excede um determinado valor. No caso de usar um filtro passa-baixo digital, a escolha da largura de banda permite alterar a frequência de corte, afetando inevitavelmente a velocidade de resposta do sensor às mudanças de posição no espaço. A frequência de corte deve ser menor que a metade da taxa de dados de saída digital (ODR), também chamada frequência de Nyquist.

Para acelerômetros MPU-9250, os limites da largura de banda são determinados de modo que dentro da faixa a densidade espectral do sinal difira do pico (a uma frequência de 0 Hz) não superior a -3 dB. Esse nível corresponde aproximadamente a uma queda para metade da densidade espectral (ou 70,7% da amplitude espectral de pico). Deixe-me lembrá-lo, para quantidades de energia (potência, energia, densidade de energia) proporcional aos quadrados da força do campo, expressos em decibéis, a razão

$$

$$D_P = 10 \ lg {P_2 \ sobre {P_1}}$$

.
Conclusão: os sinais que passam pelo filtro passa-baixo são menos barulhentos, têm melhor resolução, mas menos largura de banda. Portanto, especificar resolução na especificação sem referência à largura de banda não faz sentido.

Voltar à resolução

Na especificação do MPU-9250, basicamente não há informações sobre a resolução, para o BMI088 sob o nome "Resolução", resolução digital (LSB) e sensibilidade são apresentadas ":



A resolução para cada largura de banda pode ser estimada pelo pico de ruído. $$$Ruído_ {pk-pk} = Ruído total_ {RMS} \ times CrestFactor = Ruído total_ {RMS} \ vezes 4.$ O valor médio quadrático raiz do ruído na saída está relacionado à densidade espectral especificada na especificação (ou melhor, a raiz dele) e a largura de banda de ruído equivalente (largura de banda de ruído equivalente, ENBW) - a banda passante de um sistema equivalente com uma resposta de freqüência retangular e o mesmo valor na frequência zero do sistema original e a dispersão na saída, quando exposta às entradas dos sistemas de ruído branco):

$$

$$N_ {RMS} = PSD \ times \ sqrt {ENBW}$$

E a largura de banda do ruído é conectada à banda 3dB por coeficientes correspondentes à ordem do filtro passa-baixo:

$$

$$ENBW = 1,57 \ cdot f_ {3dB} \ textrm {para o 1º pedido}$$

$$

$$ENBW = 1,11 \ cdot f_ {3dB} \ textrm {para a segunda ordem}$$

$$

$$ENBW = 1,05 \ cdot f_ {3dB} \ textrm {para terceira ordem}$$

$$

$$ENBW = 1.025 \ cdot f_ {3dB} \ textrm {para o quarto pedido}$$

A julgar pelo estudo em [MPU9250_DLPF], nossa escolha é 1,57. O valor eficaz obtido leva em consideração a contribuição do ruído branco (não há ruído de quantização ou ruído mecânico). Por exemplo, para o acelerômetro, o valor calculado para $$$BW = 99Hz, PSD = 300 \ mu g / \ sqrt {Hz}$ acontece $$$N_ {RMS} = 4 mg$ . Nesse caso, a especificação contém o ruído eficaz total $$ A discrepância é significativa. Infelizmente, é indicado para apenas uma banda e, para o acelerômetro BMI088, apenas o PSD é indicado na especificação. Então, vamos usar o que é. Pegue o fator cruzado 4. Agora, o mais interessante. Atitude $$$FS / Ruído_ {pk-pk}$ fornecerá uma ordem aproximada de bits efetivos nessa faixa de medição, que é decentemente menor que a resolução de 16 bits do ADC.

MPU-9250			BMI088
Giroscópio
$$$\ small N ^ {Total} _ {RMS} = 0,1 ^ {\ circ} / s (PN = 92Hz)$			$$$\ small N_ {RMS} = 0,1 ^ {\ circ} / s (PN = 47Hz)$
$$$\ small PSD = 0,01 ^ {\ circ} / s / \ sqrt {Hz}$			$$$\ small PSD = 0.014 ^ {\ circ} / s / \ sqrt {Hz}$
$$$\ BW pequeno, Hz$	$$$\ small N_ {RMS}, ^ {\ circ} / s-rms$	$$$\ small N_ {PP}, ^ {\ circ} / s$	$$$\ BW pequeno, Hz$	$$$\ small N_ {RMS}, ^ {\ circ} / s$	$$$\ small N_ {PP}, ^ {\ circ} / s$
			523	0,41	1.6
250	0,2	0,8	230	0,27	1.1
184	0,17	0,69	116	0,19	0,76
92	0,12	0,49	64	0,14	0,57
41.	0,08	0,32	47	0,12	0,49
20	0,06	0,23	32.	0,1	0,4
10	0,04	0,16	23	0,09	0,34
5	0,03	0,11	12	0,06	0,25
Acelerômetro
$$$\ small N ^ {Total} _ {RMS} = 8mg \ textrm {(PN = 99Hz)}$			$$$\ small PSD_ {XY} = 160 \ mu g / \ sqrt {Hz}$
$$$\ pequeno PSD = 300 \ mu g / \ sqrt {Hz} \ textrm {(giroscópio)}$			$$$\ pequeno PSD_Z = 190 \ mu g / \ sqrt {Hz} (g_ {FS3g}, \ textrm {modo normal}$
$$$\ BW pequeno, Hz$	$$$\ pequeno N_ {RMS}, mg$	$$$\ pequeno N_ {PP}, mg$	$$$\ BW pequeno, Hz$	$$$\ small N_ {RMS_XY}, mg$	$$$\ pequeno N_ {PP_XY}, mg$
218,1	5.6	22	280	3.4.	14
99	3.8	15	145	2.4	10
44,8	2.5	10	80	1.8	7
21,2	1.7	7	40.	1.3	5
10,2	1.2	4.9	20	0,9	4
5.05	0,9	3.4.	10	0,6	2.6
420	7.8	31	5	0,5	1.8
1046	12,3	49.

Atraso (ms) ou de onde vem o atraso

Devido à necessidade de armazenar variáveis ​​no buffer interno para dividir o sinal pelo filtro em diferentes frequências

Total Quanto menor a frequência de corte do filtro, menos ruído no sinal. Mas aqui devemos ter cuidado, porque ao mesmo tempo o atraso aumenta. Além disso, você pode pular o sinal útil [8].

MPU-9250		BMI088
Giroscópio, 16 bits
Intervalo (FS) $$$^ {\ circ} / s$ (dps)	Resolução, bit (BW = 92Hz)	Intervalo (FS) $$$^ {\ circ} / s$ (dps)	Resolução, bit (BW = 64Hz)
		$$$\ pm 125$	8
$$	9	$$	9
$$	10	$$	10
$$$\ pm 1000$	11	$$$\ pm 1000$	11
$$$\ pm 2000$	12	$$$\ pm 2000$	12
Acelerômetro
Faixa (FS), g	Resolução, bit $$$(N_ {PP} = 32mg)$	Faixa (FS), g	Resolução (X, Y), bit $$$(N_ {PP} ^ XY = 14mg)$
$$$\ pm 2$	6	$$$\ pm 3$	8
$$$\ pm 4$	7	$$$\ pm 6$	9
$$$\ pm 8$	8	$$$\ pm 12$	10
$$	9	$$$\ pm 24$	11

E esses são apenas os parâmetros mais básicos.

De onde veio isso:

1. O documento mais agradável da Freescale Semiconductor é "Quantos bits são suficientes?"
2. [EE] - “Resolução x precisão x sensibilidade cortando a confusão”
3. [Tempo da eletrônica] - “Sensores de movimento MEMS da STMicroelectronics: acelerômetros e giroscópios”
4. [LSB] - “Um bit menos significativo para ADC e DAC (LSB)”
5. [Computação de medição] - “Dica técnica: exatidão, precisão, resolução e sensibilidade”
6. [KIT] - “Acelerômetros de dispositivos analógicos - Dispositivo e aplicação”
7. [Easyelectronics] - “Sigma-Delta ADC”
8. [Radiolotsman] - “Magnetômetros: princípio de operação, compensação de erro”
9. [SO] - "Medição de ruído"
10. [Mide] - “Especificações do acelerômetro: decifrando a folha de dados de um acelerômetro”
11. [CiberLeninka] - Filtro ADC Delta-Sigma
12. [SciEd] - “Características da implementação da filtragem digital com alteração na frequência de amostragem”
13. [MPU6050] - “Usando o DLPF do MPU6050”
14. [MPU9250_DLPF] - investigação de trabalho MPU9250 Gyro Noise DLPF
15. Compreendendo as especificações de resolução do sensor
16. Processamento de sinal digital da Siemens
17. Sensores de movimento MEMS da STMicroelectronics
18. [TMWorld] - "Avaliando unidades de medida inercial"
19. [Sklyar] - Sklyar B. Comunicação digital. Fundamentos teóricos e aplicação prática.