Latência de aprendizado: teoria das filas

O tema da latência ao longo do tempo se torna interessante em diferentes sistemas no Yandex e não apenas. Isso acontece quando qualquer garantia de serviço aparece nesses sistemas. Obviamente, o fato é que é importante não apenas prometer alguma oportunidade aos usuários, mas também garantir seu recebimento com um tempo de resposta razoável. A “racionalidade” do tempo de resposta, é claro, varia muito para sistemas diferentes, mas os princípios básicos pelos quais a latência se manifesta em todos os sistemas são comuns e podem ser considerados isoladamente dos específicos.

Meu nome é Sergey Trifonov, trabalho na equipe de Redução em tempo real do mapa em Yandex. Estamos desenvolvendo uma plataforma para processamento de fluxo de dados em tempo real com tempos de resposta de segundo e subsegundo. A plataforma está disponível para usuários internos e permite que eles executem o código do aplicativo em fluxos de dados constantemente recebidos. Tentarei dar uma breve visão geral dos conceitos básicos da humanidade sobre o tópico da análise de latência nos últimos cento e dez anos, e agora tentaremos entender o que exatamente pode ser aprendido sobre latência usando a teoria das filas.

O fenômeno da latência começou a ser sistematicamente investigado, tanto quanto eu sei, em conexão com o advento dos sistemas de filas - redes de comunicação telefônica. A teoria das filas começou com o trabalho de A.K. Erlang em 1909, no qual ele mostrou que a distribuição de Poisson é aplicável ao tráfego telefônico aleatório. Erlang desenvolveu uma teoria que tem sido usada há décadas para projetar redes telefônicas. A teoria nos permite determinar a probabilidade de uma negação de serviço. Para redes telefônicas com canais de circuito comutado, ocorreu uma falha se todos os canais estiverem ocupados e a chamada não puder ser feita. A probabilidade desse evento teve que ser controlada. Eu queria ter uma garantia de que, por exemplo, 95% de todas as chamadas seriam atendidas. As fórmulas de Erlang possibilitam determinar quantos servidores são necessários para cumprir essa garantia se a duração e o número de chamadas forem conhecidos. De fato, essa tarefa trata apenas de garantias de qualidade e hoje as pessoas ainda resolvem problemas semelhantes. Mas os sistemas se tornaram muito mais complexos. O principal problema da teoria das filas é que ela não é ensinada na maioria das instituições, e poucas pessoas entendem a pergunta fora da fila M / M / 1 usual (veja a notação abaixo ), mas é sabido que a vida é muito mais complicada do que esse sistema. Portanto, proponho, contornando M / M / 1, ir imediatamente para o mais interessante.

Valores médios

Se você não tentar obter conhecimento completo sobre a distribuição de probabilidade no sistema, mas se concentrar em perguntas mais simples, poderá obter resultados interessantes e úteis. O mais famoso deles é, obviamente, o teorema de Little . É aplicável a um sistema com qualquer fluxo de entrada, dispositivo interno de qualquer complexidade e um planejador arbitrário. O único requisito é que o sistema seja estável: os tempos médios de resposta e os comprimentos das filas devem existir e, em seguida, eles serão conectados por uma expressão simples

$$

$$L = \ lambda W$$

onde $$$L$ - o número médio de pedidos na parte considerada do sistema [pcs], $$$W$ - o tempo médio pelo qual os pedidos passam por essa parte do sistema, $$$\ lambda$ - a velocidade de recebimento de solicitações ao sistema [pcs / s]. A força do teorema é que ele pode ser aplicado a qualquer parte do sistema: fila, executor, fila + executor ou toda a rede. Muitas vezes, esse teorema é usado aproximadamente assim: "O fluxo de 1 Gbit / s está fluindo em nossa direção e medimos o tempo médio de resposta, e são 10 ms; portanto, em média, temos 1,25 MB em voo". Portanto, esse cálculo não é verdadeiro. Mais precisamente, isso é verdade apenas se todas as solicitações tiverem o mesmo tamanho em bytes. O teorema de Little conta consultas em pedaços, não em bytes.

Como usar o teorema de Little

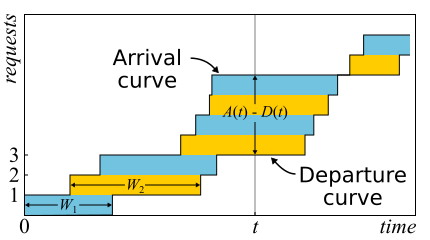
Em matemática, muitas vezes é necessário estudar evidências para obter uma visão real. Este é apenas o caso. O teorema de Little é tão bom que apresento aqui um esboço da prova. O tráfego de entrada é descrito pela função $$$A (t)$ - o número de solicitações que estão conectadas no momento $$$t$ . Da mesma forma $$$D (t)$ - o número de solicitações desconectadas no momento $$$t$ . O momento de entrada (saída) da solicitação é considerado o momento de recebimento (transmissão) de seu último byte. Os limites do sistema são determinados apenas por esses instantes de tempo; portanto, o teorema é amplamente aplicável. Se você desenhar gráficos dessas funções nos mesmos eixos, é fácil ver que $$$A (t) - D (t)$ É o número de solicitações no sistema no momento t, e $$$W_n$ - tempo de resposta da enésima solicitação.

O teorema foi formalmente provado apenas em 1961, embora a relação em si fosse conhecida muito antes disso.

De fato, se as solicitações puderem ser reordenadas dentro do sistema, tudo será um pouco mais complicado; portanto, por simplicidade, assumiremos que isso não acontece. Embora o teorema seja verdadeiro também neste caso. Agora vamos calcular a área entre os gráficos. Existem duas maneiras de fazer isso. Em primeiro lugar, de acordo com as colunas - como as integrais costumam pensar. Nesse caso, verifica-se que o integrando é o tamanho da fila em pedaços. Em segundo lugar, linha por linha - simplesmente adicionando a latência de todas as solicitações. É claro que ambos os cálculos dão a mesma área, portanto são iguais. Se ambas as partes dessa igualdade são divididas pelo tempo Δt, para o qual calculamos a área, então, à esquerda, teremos o comprimento médio da fila $$$L$ (por definição da média). À direita é um pouco mais complicado. Precisamos adicionar outro número de solicitações N ao numerador e denominador, para que tenhamos sucesso.

$$

$$\ frac {\ sum W_i} {\ Delta t} = \ frac {\ sum W_i} {N} \ frac {N} {\ Delta t} = W \ lambda$$

Se considerarmos Δt suficientemente grande ou um período de emprego, as perguntas nas bordas são removidas e o teorema pode ser considerado comprovado.

É importante dizer que, na prova, não usamos distribuições de probabilidades. De fato, o teorema de Little é uma lei determinística! Tais leis são chamadas na teoria das filas do direito operacional. Eles podem ser aplicados a qualquer parte do sistema e a qualquer distribuição de várias variáveis ​​aleatórias. Essas leis formam um construtor que pode ser usado com sucesso para analisar valores médios em redes. A desvantagem é que todos eles se aplicam apenas às médias e não fornecem nenhum conhecimento sobre as distribuições.

Voltando à questão de por que o teorema de Little não pode ser aplicado a bytes, suponha que $$$A (t)$ e $$$D (t)$ agora eles são medidos não em pedaços, mas em bytes. Então, conduzindo um argumento semelhante, obtemos $$$W$ o estranho é a área dividida pelo número total de bytes. Ainda falta alguns segundos, mas é uma latência média ponderada em que solicitações maiores ganham mais peso. Esse valor pode ser chamado de latência média do byte - que, em geral, é lógico, pois substituímos partes por bytes - mas não a latência da solicitação.

O teorema de Little diz que, com um certo fluxo de solicitações, o tempo de resposta e o número de solicitações no sistema são proporcionais. Se todas as solicitações parecerem iguais, o tempo médio de resposta não poderá ser reduzido sem aumentar a potência. Se soubermos o tamanho das consultas com antecedência, podemos tentar reordená-las para reduzir a área entre $$$A (t)$ e $$$D (t)$ e, portanto, o tempo médio de resposta do sistema. Continuando com essa idéia, podemos provar que os algoritmos Menor Tempo de Processamento e Menor Tempo de Processamento Restante fornecem um tempo médio de resposta mínimo para um servidor, sem a possibilidade de se agrupar com ele, respectivamente. Mas há um efeito colateral - solicitações grandes podem não ser processadas indefinidamente. O fenômeno é chamado de "inanição" e está intimamente relacionado ao conceito de justiça do planejamento, que pode ser aprendido em um post anterior no agendamento: mitos e realidade .

Existe outra armadilha comum associada à compreensão da lei de Little. Há um servidor de thread único que atende a solicitações do usuário. Suponha que de alguma forma medimos L - o número médio de solicitações na fila para este servidor e S - o tempo médio em que o servidor atendeu a uma solicitação. Agora considere uma nova solicitação de entrada. Em média, ele vê L consultas à sua frente. Servir cada um deles leva em média S segundos. Acontece que o tempo médio de espera $$$W = L S$ . Mas pelo teorema verifica-se que $$$W = L / \ lambda$ . Se equipararmos as expressões, veremos o absurdo: $$$S = 1 / \ lambda$ . O que há de errado com esse raciocínio?

1. A primeira coisa que chama sua atenção: o tempo de resposta do teorema não depende de S. Na verdade, é claro, depende. Apenas o tamanho médio da fila já leva isso em consideração: quanto mais rápido o servidor, menor o comprimento da fila e menor o tempo de resposta.
2. Consideramos um sistema no qual as filas não se acumulam para sempre, mas são redefinidas regularmente. Isso significa que a utilização do servidor é inferior a 100% e pulamos todas as solicitações recebidas e na mesma velocidade média com a qual essas solicitações chegaram, o que significa que, em média, não leva S segundos, mas mais, para processar uma solicitação $$$1 / \ lambda$ segundos, simplesmente porque às vezes não processamos nenhuma solicitação. O fato é que, em qualquer sistema aberto estável sem perda, a taxa de transferência não depende da velocidade dos servidores, é determinada apenas pelo fluxo de entrada.
3. A suposição de que uma solicitação recebida vê no sistema um número médio de solicitações nem sempre é verdadeira. Contra-exemplo: as solicitações recebidas são enviadas periodicamente e conseguimos processar cada solicitação antes da chegada da próxima. Uma imagem típica para sistemas em tempo real. Uma solicitação recebida sempre vê zero solicitações no sistema, mas, em média, o sistema obviamente tem mais de zero solicitações. Se as solicitações ocorrerem em horários completamente aleatórios, elas realmente "verão o número médio de solicitações" .
   
   
   
4. Não levamos em conta que, com uma certa probabilidade, já pode haver uma solicitação no servidor que precisa ser "estendida". No caso geral, o tempo médio de "serviço pós-atendimento" difere do tempo inicial de serviço e, às vezes, paradoxalmente , pode ser muito mais longo. Voltaremos a esta questão no final, quando discutirmos sobre micro-explosões, fique atento.

Portanto, o teorema de Little pode ser aplicado a sistemas grandes e pequenos, a filas, a servidores e a threads de processamento único. Mas em todos esses casos, as solicitações geralmente são classificadas de uma maneira ou de outra. Solicitações de usuários diferentes, solicitações de prioridades diferentes, solicitações provenientes de locais diferentes ou solicitações de tipos diferentes. Nesse caso, as informações agregadas por classes não são interessantes. Sim, o número médio de pedidos mistos e o tempo médio de resposta para todos eles são novamente proporcionais. Mas e se quisermos saber o tempo médio de resposta para uma determinada classe de solicitações? Surpreendentemente, o teorema de Little pode ser aplicado a uma classe específica de consultas. Nesse caso, você precisa tomar como $$$\ lambda$ A taxa na qual essa classe solicita, não todas. Como $$$L$ e $$$W$ - valores médios do número e tempo de permanência dos pedidos desta classe na parte investigada do sistema.

Sistemas abertos e fechados

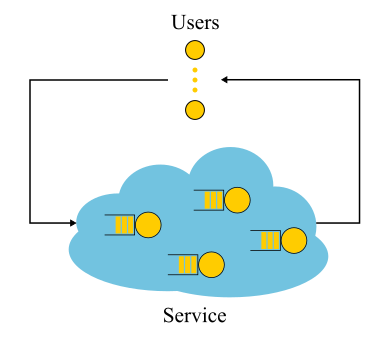
É importante notar que, para sistemas fechados, a linha de raciocínio “errada” que leva à conclusão $$$S = 1 / \ lambda$ acaba por ser verdade. Sistemas fechados são aqueles em que os pedidos não vêm de fora e não saem, mas circulam por dentro. Ou, caso contrário, sistemas de feedback: assim que a solicitação sai do sistema, uma nova solicitação ocorre. Esses sistemas também são importantes porque qualquer sistema aberto pode ser considerado imerso em um sistema fechado. Por exemplo, você pode considerar o site como um sistema aberto, no qual as solicitações são constantemente derramadas, processadas e retiradas ou, inversamente, como um sistema fechado com todo o público do site. Em geral, eles dizem que o número de usuários é fixo e esperam uma resposta à solicitação ou "pensam": eles receberam sua página e ainda não clicaram no link. No caso de pensar que o tempo é sempre zero, o sistema também é chamado de sistema em lote.

A lei de Little para sistemas fechados é válida se a velocidade de chegadas externas $$$\ lambda$ (eles não estão em um sistema fechado) substitua pela largura de banda do sistema. Se envolvermos o servidor de thread único discutido acima em um sistema em lote, obteremos $$$S = 1 / \ lambda$ e 100% de reciclagem. Muitas vezes, essa análise do sistema fornece resultados inesperados. Nos anos 90, foi precisamente essa visão da Internet, juntamente com os usuários como um sistema único, que deu impulso ao estudo de distribuições que não eram exponenciais. Discutiremos ainda mais as distribuições, mas aqui observamos que quase tudo e em toda parte era considerado exponencial, e até isso foi encontrada alguma justificativa, e não apenas uma desculpa no espírito de "caso contrário, muito complicado". No entanto, descobriu-se que nem todas as distribuições praticamente importantes têm caudas igualmente longas, e o conhecimento das caudas de distribuição pode ser tentado. Mas, por enquanto, vamos voltar aos valores médios.

Efeitos relativísticos

Suponha que tenhamos um sistema aberto: uma rede complexa ou um servidor simples de thread único - isso não importa. O que mudará se dobrarmos a chegada de solicitações e acelerarmos o processamento pela metade - por exemplo, dobrando a capacidade de todos os componentes do sistema? Como a utilização, a taxa de transferência, o número médio de solicitações no sistema e o tempo médio de resposta mudam? Para um servidor de thread único, você pode tentar pegar as fórmulas, aplicá-las “na testa” e obter os resultados, mas o que fazer com uma rede arbitrária? A solução intuitiva é a seguinte. Suponha que o tempo seja dobrado e, em nosso "sistema de referência acelerado", a velocidade dos servidores e o fluxo de solicitações não parecem mudar; consequentemente, todos os parâmetros em tempo acelerado têm os mesmos valores de antes. Em outras palavras, a aceleração de todas as "partes móveis" de qualquer sistema é equivalente à aceleração do relógio. Agora vamos converter os valores em um sistema com um horário normal. Quantidades sem dimensão (utilização e número médio de solicitações) não serão alteradas. Valores cuja dimensão inclui fatores de tempo de primeiro grau variam proporcionalmente. A taxa de transferência de [solicitações / s] será duplicada e os tempos de resposta e espera [s] serão reduzidos pela metade.

Este resultado pode ser interpretado de duas maneiras:

1. Um sistema acelerado por k vezes pode digerir o fluxo de tarefas k vezes mais e com um tempo médio de resposta k vezes menor.
2. Podemos dizer que o poder não mudou, mas simplesmente o tamanho das tarefas diminuiu k vezes. Acontece que estamos enviando a mesma carga para o sistema, mas serrados em pedaços menores. E ... oh, um milagre! O tempo médio de resposta é reduzido!

Mais uma vez, observo que isso é verdade para uma ampla classe de sistemas, e não apenas para um servidor simples. Do ponto de vista prático, existem apenas dois problemas:

1. Nem todas as partes do sistema podem ser facilmente aceleradas. Não podemos influenciar alguns. Por exemplo, a velocidade da luz.
2. Nem todas as tarefas podem ser infinitamente divididas em menores e menores, uma vez que as informações não foram aprendidas a serem transferidas em partes de menos de um bit.

Considere a passagem até o limite. Suponhamos, no mesmo sistema aberto, a interpretação número 2. Dividimos cada solicitação recebida pela metade. O tempo de resposta também é dividido pela metade. Repita a divisão várias vezes. E nem precisamos mudar nada no sistema. Acontece que você pode reduzir o tempo de resposta arbitrariamente simplesmente vendo os pedidos recebidos em um número suficientemente grande de peças. No limite, podemos dizer que, em vez de consultas, obtemos um "fluido de consulta", que filtramos por nossos servidores. Este é o chamado modelo de fluido, uma ferramenta muito conveniente para análise simplificada. Mas por que o tempo de resposta é zero? O que deu errado? Onde não consideramos a latência? Acontece que não levamos em conta apenas a velocidade da luz, ela não pode ser duplicada. O tempo de propagação no canal da rede não pode ser alterado, você só pode aguentar. De fato, a transmissão através de uma rede inclui dois componentes: tempo de transmissão e tempo de propagação. O primeiro pode ser acelerado aumentando a potência (largura do canal) ou reduzindo o tamanho dos pacotes, e o segundo é muito difícil de influenciar. Em nosso "modelo líquido", simplesmente não havia reservatórios para acumular líquidos - canais de rede com tempos de propagação diferentes de zero e constantes. A propósito, se os adicionarmos ao nosso "modelo líquido", a latência será determinada pela soma dos tempos de propagação e as filas nos nós ainda estarão vazias. As filas dependem apenas dos tamanhos dos pacotes e da variabilidade (leitura intermitente) do fluxo de entrada.

Daqui resulta que, no que diz respeito à latência, você não pode se dar bem com o cálculo de fluxos, e mesmo os dispositivos de reciclagem não resolvem tudo. É necessário levar em consideração o tamanho das solicitações e não esquecer o tempo de distribuição, que geralmente é ignorado na teoria das filas, embora não seja difícil adicioná-lo aos cálculos.

Distribuições

Qual é o motivo da fila? Obviamente, o sistema não tem capacidade suficiente e o excesso de solicitações está se acumulando? Não é verdade! As filas também surgem em sistemas onde existem recursos suficientes. Se não houver capacidade suficiente, o sistema, como dizem os teóricos, não é estável. Há duas razões principais para a fila: a irregularidade das solicitações e a variabilidade do tamanho das solicitações. Já examinamos um exemplo no qual essas duas razões foram eliminadas: um sistema em tempo real em que solicitações do mesmo tamanho são feitas estritamente periodicamente. Uma fila nunca se forma. O tempo médio de espera na fila é zero. , , , . , .

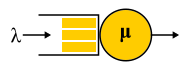
A/S/k/K, A — , S — , k — , K — (, ). , M/M/1 : M (Markovian Memoryless) , . : $$$\lambda$ — — , : . M , μ . , , . , 4- . , , : G — (, , ), D — deterministic. C — D/D/1. , 1909 ., — M/D/1. — M/G/k k>1, M/G/1 1930-.

?

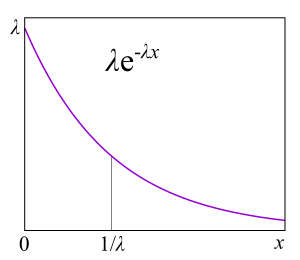
, , , , , . , . , failure rate . , , : , . failure rate function, . , «» , . , : , . , failure rate — , , - , — . , , , , , . « ».

Failure rate . — . Failure rate , , , . failure rate, , , . failure rate, , , . , , , software hardware? : ? . , , - . ? , — . ( failure rate) . « » .

, , failure rate, , , unix- . , .

RTMR , . LWTrace - . . , . , $$$\mathbf{P}\{S>x\}$ . , failure rate , , : .



$$$\mathbf{P}\{S>x\} = x^{-a}$ , — . , « », 80/20: , . . , . , RTMR -, , . $$$a=1.16$ , 80/20: 20% 80% .

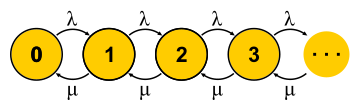
, . . , , , - . , — . « » , « » — . : , ? , ( , ), . , 0 . , , $$$\mu N_1$ $$$\lambda N_0$ . , , — . . , . M/M/1 $$$\mathbf{P}\{Q=i\} = (1 - \rho) \rho^i$ onde $$$\rho = \lambda / \mu$ - Esta é a utilização do servidor. O fim da história. No decorrer da apresentação, perdi uma quantidade razoável de suposições e fiz algumas substituições de conceitos, mas espero que a essência não tenha sofrido.

É importante entender que essa abordagem só funciona se o estado atual da máquina determinar completamente seu comportamento adicional, e a história de como ela entrou nesse estado não é importante. Para a compreensão cotidiana de uma máquina de estados finitos, isso é desnecessário - afinal, é uma condição para isso. Mas, para um processo estocástico, segue-se que todas as distribuições devem ser exponenciais, uma vez que apenas elas não têm memória - elas têm uma taxa de falha constante.

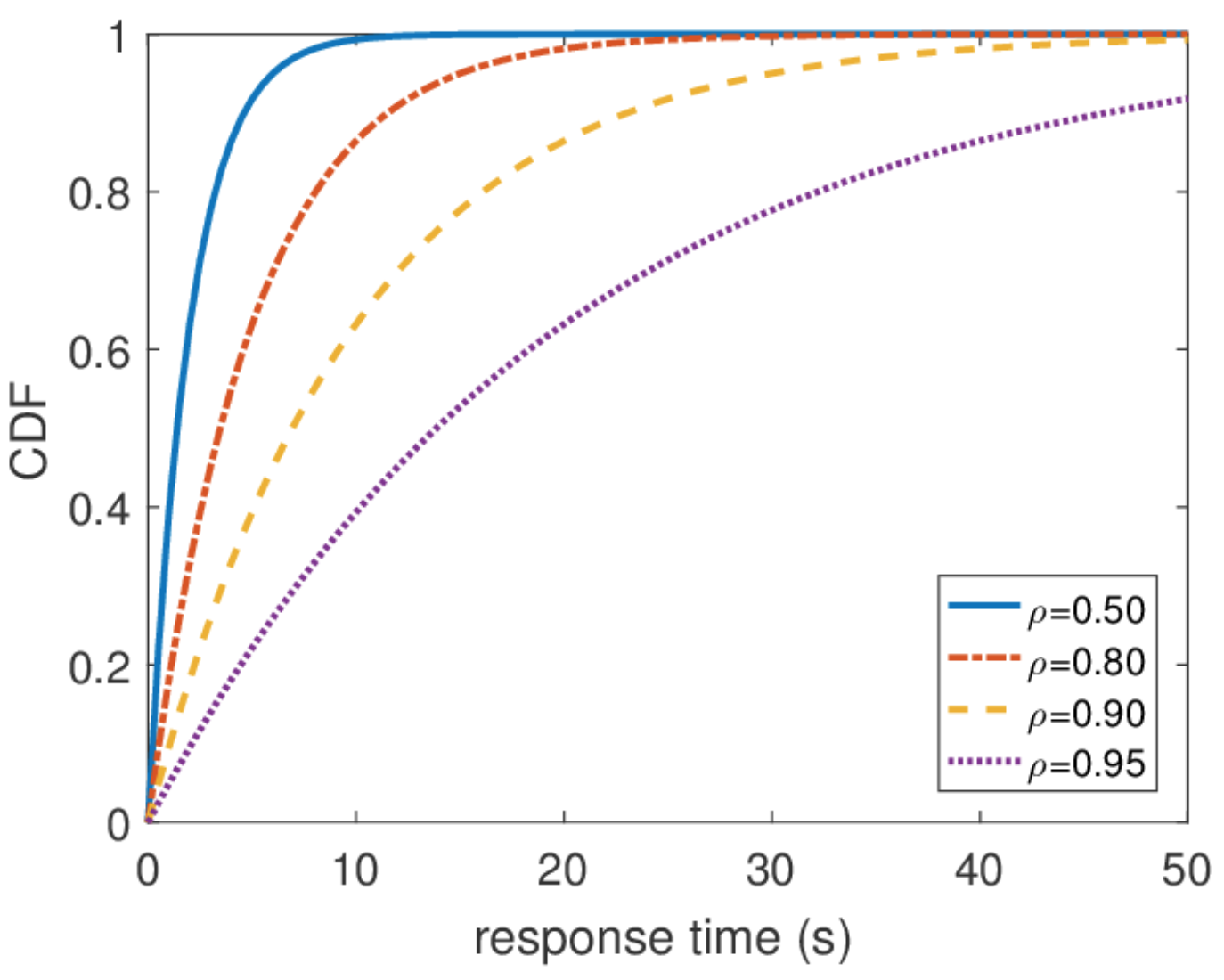
Também é importante dizer que todas as outras informações sobre o sistema são fáceis de obter se conhecermos a distribuição de equilíbrio. O número médio de consultas no sistema é a média dessa distribuição. Para descobrir o tempo médio de resposta, aplicamos o teorema de Little ao número de consultas. A distribuição do tempo de resposta é um pouco mais difícil de encontrar, mas também em algumas ações você pode descobrir que $$$\ mathbf {P} \ {response \ _time> t \} = e ^ {- (\ mu- \ lambda) t}$ e qual é o tempo médio de resposta $$$1 / (\ mu- \ lambda)$ .

Tempo de resposta ilimitado

A partir dessa distribuição, você pode encontrar qualquer percentil do tempo de resposta, e o centésimo percentil é igual ao infinito. Em outras palavras, o pior tempo de resposta não é limitado de cima. O que, em geral, não é surpreendente, pois usamos o fluxo de Poisson. Mas, na prática, esse comportamento nunca pode ser encontrado. Obviamente, o fluxo de entrada de solicitações ao servidor é limitado, pelo menos pela largura do canal de rede para este servidor, e o comprimento da fila é limitado pela memória nesse servidor. O fluxo de Poisson, pelo contrário, com probabilidade diferente de zero garante a ocorrência de explosões arbitrariamente grandes. Portanto, eu não recomendaria proceder da suposição de um fluxo de entrada Poisson ao projetar um sistema se você estiver interessado em altos percentis e a carga do sistema for muito alta. É melhor usar outros modelos de tráfego, sobre os quais falarei outra vez sobre o cálculo da rede.

Escala e garantias

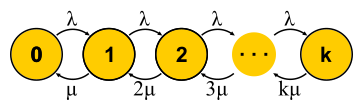
Agora que temos uma maneira poderosa o suficiente para analisar sistemas, podemos tentar aplicá-lo a diferentes tarefas e colher os benefícios. Foi assim que a teoria do serviço de massa se desenvolveu na segunda metade do século XX. Vamos tentar entender o que foi alcançado. Para começar, voltemos às tarefas que Erlang resolveu. Essas são as tarefas M / M / k / k e M / M / k, nas quais gostaríamos de limitar a probabilidade de falha. Acontece que não é difícil para eles construir cadeias de Markov. A diferença é que, à medida que as tarefas são adicionadas, a probabilidade de uma transição reversa aumenta, pois as tarefas começam a ser processadas em paralelo, mas quando o número de tarefas se torna igual ao número de servidores, ocorre saturação. Além disso, para M / M / k / k, a rede termina, o autômato realmente é finito e todas as solicitações que chegam ao último estado são negadas. A probabilidade deste evento é simplesmente igual à probabilidade de estarmos no último estado.

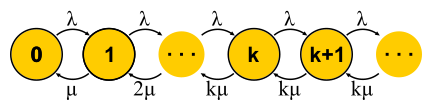
Para M / M / k, a situação é mais complicada, as solicitações são enfileiradas, novos estados aparecem, mas a probabilidade de uma transição reversa não aumenta - todos os servidores já estão funcionando. A rede se torna infinita, como para M / M / 1. A propósito, se o número de solicitações no sistema for limitado, a cadeia sempre terá um número finito de estados e, de uma forma ou de outra, será resolvida, o que não pode ser dito sobre as intermináveis ​​cadeias. Em sistemas fechados, as correntes são sempre finitas. Resolvendo os circuitos descritos para M / M / k / k e M / M / k, chegamos à fórmula B e à fórmula C de Erlang , respectivamente. Eles são bastante volumosos, não darei a eles, mas com a ajuda deles, você pode obter um resultado interessante para o desenvolvimento da intuição, que é chamada de regra de pessoal da raiz quadrada. Suponha que exista um sistema M / M / k com algum fluxo de entrada fornecido λ de solicitações por segundo. Suponha que a carga dobrará até amanhã. A questão é: como aumentar o número de servidores para que o tempo de resposta permaneça o mesmo? O número de servidores precisa ser dobrado, certo? Acontece que não. Lembre-se de que já vimos: se você acelerar o tempo (servidores e login) pela metade, o tempo médio de resposta diminuirá pela metade. Vários servidores lentos e um rápido não são a mesma coisa, mas, no entanto, o poder da computação é o mesmo. Em particular, para M / M / 1, por exemplo, o tempo de resposta é inversamente proporcional ao volume de "capacidade livre" $$$\ mu - \ lambda$ e é determinado apenas por este volume. Ao dobrar o fluxo e o poder de processamento, a capacidade livre do sistema dobra: $$$2 \ mu - 2 \ lambda$ . Pode parecer que, para resolver o problema, você só precisa economizar a capacidade livre, mas o tempo de resposta em M / M / k já é determinado pela fórmula mais complexa de Erlang. Acontece que a capacidade livre deve ser mantida na proporção da raiz quadrada do número de "servidores ocupados" para manter o mesmo tempo de resposta. Por número de “servidores ocupados” entende-se o número total de servidores multiplicado pela utilização: este é o número mínimo de servidores necessários para uma operação estável.

Usando essa regra, às vezes eles tentam justificar como expandir um cluster com servidores. Mas não fique com a ilusão de que qualquer cluster é um sistema M / M / k. Por exemplo, se você possui um balanceador em sua entrada que envia solicitações em filas para servidores, isso não é mais M / M / k, pois M / M / k implica uma fila comum na qual os servidores capturam solicitações quando são liberadas. Mas esse modelo é adequado, por exemplo, para conjuntos de encadeamentos com uma fila FIFO comum. No entanto, mesmo neste caso, vale lembrar que esta regra é uma aproximação para o caso em que existem muitos encadeamentos. De fato, se você tiver mais de 10 threads, poderá assumir com segurança que existem muitos deles. Bem, não se esqueça das distribuições exponenciais onipresentes: sem assumir a exponencialidade de todas as distribuições, a regra também não funciona.

Tempo de resposta da rede

Por fim, é interessante uma rede de M / M / k conectada pelo menos em uma cadeia, já que fabricamos sistemas distribuídos. Para estudar redes, eu gostaria de ter um construtor: regras simples e claras para conectar elementos conhecidos em blocos. Na teoria de controle, por exemplo, existem funções de transferência que são compreensivelmente combinadas com conexões seriais ou paralelas. Aqui, o fluxo de saída de qualquer nó tem uma distribuição muito complicada, com exceção de M / M / k, que, de acordo com o conhecido teorema de Burke, produz um fluxo de Poisson independente. Essa exceção, como você pode imaginar, é usada principalmente.

A conexão de dois fluxos Poisson é um fluxo Poisson. A separação probabilística do fluxo de Poisson em dois produz novamente dois fluxos de Poisson. Tudo isso leva ao fato de que todas as filas do sistema são independentes e você pode obter, em linguagem formal, a chamada solução de formulário de produto . Ou seja, a distribuição conjunta dos comprimentos das filas é simplesmente o produto das distribuições dos comprimentos de todas as filas, consideradas separadamente - é assim que a independência é expressa na teoria das probabilidades. Apenas encontramos os fluxos de entrada para todos os nós e usamos as fórmulas para cada nó de forma independente. Existem várias limitações:

1. Algoritmo de roteamento probabilístico. A solicitação atendida pelo nó seleciona a próxima aleatoriamente com uma probabilidade conhecida. Isso não é tão ruim quanto parece, porque é possível usar "classes de solicitação": digamos que todas as solicitações de Vasya cheguem ao servidor nº 1, depois ao servidor nº 2 e depois saiam da rede, e as solicitações de Petya venham ao servidor nº 2 e, com igual probabilidade, visite o servidor número 1 ou número 3 e saia. Ou seja, nem todas as transições precisam ser aleatórias, algumas ou mesmo todas podem ter uma probabilidade de 100%.
2. Suposição da independência de Kleinrock. O tempo de processamento da solicitação não pode depender do histórico ou da classe da solicitação, mas é determinado apenas pelo servidor e, quando a solicitação passa novamente pelo mesmo servidor, é selecionado aleatoriamente a cada vez. De fato, não há como definir o tamanho da solicitação que seria usada em servidores diferentes, e o tempo de serviço é determinado apenas pelo próprio servidor. Você também pode tentar contornar essa limitação. Para isso, o roteamento probabilístico é geralmente usado e é feito um loop para retornar ao mesmo servidor com alguma probabilidade - como se eles reiniciassem a solicitação. Na minha opinião, esse é um truque bastante estranho, porque essa solicitação entra novamente na fila e não é executada imediatamente, mas para algumas tarefas isso não é importante.
3. Tráfego de entrada de Poisson e tempo de serviço exponencial em todos os nós.

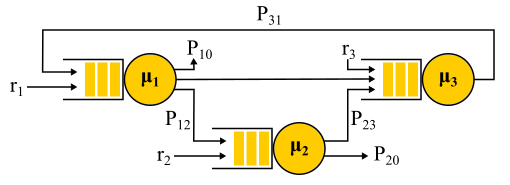
Exemplo de rede Jackson.

Vale a pena notar que, na presença de feedback, um fluxo de Poisson NÃO é obtido, pois os fluxos acabam sendo interdependentes. Na saída do nó de feedback, também é obtido um fluxo não Poisson e, como resultado, todos os fluxos se tornam não Poisson. No entanto, de uma maneira surpreendente, verifica-se que todos esses fluxos não-Poisson se comportam exatamente da mesma forma que os fluxos Poisson (oh, essa teoria da probabilidade) se as restrições acima forem atendidas. E, novamente, obtemos uma solução em forma de produto. Essas redes são chamadas de redes Jackson , podem fornecer feedback e, portanto, várias visitas a qualquer servidor. Existem outras redes nas quais mais liberdades são permitidas, mas, como resultado, todas as conquistas analíticas significativas da teoria das filas em relação às redes envolvem fluxos de Poisson na solução de entrada e na forma de produto, que se tornou alvo de críticas a essa teoria e levou nos anos 90 a o desenvolvimento de outras teorias e o estudo do que é realmente necessária a distribuição e como trabalhar com elas.

Uma aplicação importante de toda essa teoria das redes Jackson é a modelagem de pacotes em redes IP e redes ATM. O modelo é bastante adequado: os tamanhos dos pacotes não variam muito e não dependem do próprio pacote, apenas da largura do canal, pois o tempo de serviço corresponde ao horário em que o pacote foi enviado ao canal. O tempo de envio aleatório, embora pareça selvagem, na verdade não possui uma variabilidade muito grande. Além disso, verifica-se que em uma rede com tempo de serviço determinístico, a latência não pode ser maior do que em uma rede Jackson semelhante; portanto, essas redes podem ser usadas com segurança para estimar o tempo de resposta de cima.

Distribuições não-exponenciais

Todos os resultados dos quais falei estavam relacionados a distribuições exponenciais, mas também mencionei que as distribuições reais são diferentes. Há um sentimento de que toda essa teoria é bastante inútil. Isto não é inteiramente verdade. Existe uma maneira de integrar outras distribuições nesse aparato matemático, além disso, praticamente todas as distribuições, mas isso nos custará algo. Com exceção de alguns casos interessantes, a oportunidade de obter uma solução de forma explícita é perdida, a solução de forma de produto é perdida e, com ela, o construtor: cada problema deve ser resolvido totalmente do zero usando cadeias de Markov. Para a teoria, esse é um grande problema, mas, na prática, significa simplesmente a aplicação de métodos numéricos e torna possível resolver problemas muito mais complexos e próximos da realidade.

Método de fase

A ideia é simples. As cadeias de Markov não nos permitem ter memória dentro de um estado; portanto, todas as transições devem ser aleatórias com uma distribuição exponencial de tempo entre duas transições. Mas e se o estado for dividido em vários subestados? As transições entre subestados ainda devem ter uma distribuição exponencial se queremos que toda a estrutura permaneça uma cadeia de Markov, e realmente queremos, porque sabemos como resolver essas cadeias. Os sub-estados são freqüentemente chamados de fases se forem organizados em série, e o processo de partição é chamado de método de fase.

O exemplo mais simples. A solicitação é processada em várias fases: primeiro, por exemplo, lemos os dados necessários do banco de dados, depois executamos alguns cálculos e depois escrevemos os resultados no banco de dados. Suponha que todos esses três estágios tenham a mesma distribuição exponencial de tempo. Qual distribuição tem o tempo de trânsito das três fases juntas? Esta é a distribuição de Erlang.



Mas e se você fizer muitas, muitas fases curtas e idênticas? No limite, obtemos uma distribuição determinística. Ou seja, ao construir uma cadeia, você pode reduzir a variabilidade da distribuição.

É possível aumentar a variabilidade? Fácil. Em vez de uma cadeia de fases, usamos categorias alternativas, escolhendo aleatoriamente uma delas. Um exemplo Quase todas as solicitações são executadas rapidamente, mas há uma pequena chance de uma solicitação enorme chegar, o que leva muito tempo. Essa distribuição terá uma taxa de falha decrescente. Quanto mais esperarmos, maior a probabilidade de a solicitação cair na segunda categoria.



Continuando a desenvolver o método das fases, os teóricos descobriram que há uma classe de distribuições com a qual você pode abordar com precisão uma distribuição arbitrária e não negativa! A distribuição de Coxian é construída pelo método das fases, apenas não somos obrigados a passar por todas as fases, após cada fase há alguma probabilidade de conclusão.



Esse tipo de distribuição pode ser usado tanto para gerar um fluxo de entrada não Poisson quanto para criar um tempo de serviço não exponencial. Aqui, por exemplo, está a cadeia de Markov para o sistema M / E2 / 1 com distribuição Erlang para o tempo de serviço. O estado é determinado por um par de números (n, s), em que n é o comprimento da fila e s é o número do estágio em que o servidor está localizado: primeiro ou segundo. Todas as combinações de n e s são possíveis. As mensagens recebidas mudam apenas n e, após a conclusão das fases, elas alternam e diminuem o comprimento da fila após a conclusão da segunda fase.

Você tem microbursts!

Um sistema carregado com metade de sua capacidade pode ficar lento? Como o primeiro sujeito de teste, preparamos M / G / 1. Dado: Fluxo de Poisson na entrada e distribuição arbitrária do tempo de serviço. Considere o caminho de uma única solicitação por todo o sistema. Um pedido recebido aleatoriamente vê na fila à sua frente o número médio de pedidos $$$\ mathbf {E} [N_Q]$ . O tempo médio de processamento para cada um deles $$$\ mathbf {E} [S]$ . Com probabilidade igual à disposição $$$\ rho$ , há outra solicitação no servidor, que deve primeiro ser "atendida" a tempo $$$\ mathbf {E} [S_e]$ . Em resumo, obtemos que o tempo total de espera na fila $$$\ mathbf {E} [T_Q] = \ mathbf {E} [N_Q] \ mathbf {E} [S] + \ rho \ mathbf {E} [S_e]$ . Pelo teorema de Little $$$\ mathbf {E} [N_Q] = \ lambda \ mathbf {E} [T_Q]$ ; combinando, obtemos:

$$

$$\ mathbf {E} [T_Q] = \ frac {\ rho} {1- \ rho} \ mathbf {E} [S_e]$$

Ou seja, o tempo de espera na fila é determinado por dois fatores. O primeiro é o efeito da utilização do servidor e o segundo é o tempo médio após o serviço. Considere o segundo fator. Uma solicitação chegando em algum momento $$$t$ , vê que os cuidados posteriores levam tempo $$$S_e (t)$ .



Tempo médio $$$\ mathbf {E} [S_e]$ determinado pelo valor médio da função $$$S_e (t)$ , ou seja, a área de triângulos dividida pelo tempo total. É claro que podemos nos limitar a um triângulo "médio", então $$$\ mathbf {E} [S_e] = \ mathbf {E} [S ^ 2] / 2 \ mathbf {E} [S]$ . Isso é bem inesperado. Recebemos que o tempo de pós-serviço é determinado não apenas pelo valor médio do tempo de serviço, mas também por sua variabilidade. A explicação é simples. A probabilidade de cair em um longo intervalo $$$S$ mais, é proporcional à duração S deste intervalo. Isso explica o famoso Paradoxo do tempo de espera, ou Paradoxo da inspeção. Mas voltando ao M / G / 1. Se você combinar tudo o que obtivemos e reescrever usando a variabilidade $$$C ^ 2_S = \ mathbf {E} [S] / \ mathbf {E} [S] ^ 2$ obtenha a famosa fórmula de Pollaczek-Khinchine :

$$

$$\ mathbf {E} [T_Q] = \ frac {\ rho} {1- \ rho} \ frac {\ mathbf {E} [S]} {2} (C ^ 2_S + 1)$$

Se a prova o aborrecer, espero que agrade o resultado de sua aplicação na prática. Já examinamos os dados de tempo de serviço no RTMR. A cauda longa surge com grande variabilidade e, neste caso, $$$C ^ 2_S = 381$ . Isso, você vê, é muito mais do que $$$C ^ 2_S = 1$ para distribuição exponencial. Em média, tudo é super rápido: $$$\ mathbf {E} [S] = 263,792 μs$ . Agora, suponha que o RTMR seja modelado pelo sistema M / G / 1 e não permita que o sistema seja carregado com muita carga. $$$\ rho = 0,5$ . Substituindo na fórmula, obtemos $$$\ mathbf {E} [T_Q] = 1 * (381 + 1) / 2 * 263,792 μs = 50 ms$ . Devido a micro-explosões, mesmo um sistema tão rápido e subutilizado pode se transformar, em média, em um nojento. Por 50 ms, você pode acessar o disco rígido seis vezes ou, se tiver sorte, até um data center em outro continente! A propósito, para G / G / 1, existe uma aproximação que leva em consideração a variabilidade do tráfego recebido: parece exatamente o mesmo, apenas $$$C ^ 2_S + 1$ é a soma das duas variedades $$$C ^ 2_S + C ^ 2_A$ . Para o caso de vários servidores, as coisas são melhores, mas o efeito de vários servidores afeta apenas o primeiro fator. O efeito da variabilidade permanece: $$$\ mathbf {E} [T_Q] ^ {G / G / k} ≈ \ mathbf {E} [T_Q] ^ {M / M / k} (C ^ 2_S + C ^ 2_A) / 2$ .

Como é o microburst? Com relação aos conjuntos de encadeamentos, essas são tarefas que são atendidas com rapidez suficiente para não serem visíveis nos planejamentos de reciclagem e lentas o suficiente para criar uma fila atrás de si e afetar o tempo de resposta do conjunto. Do ponto de vista teórico, essas são consultas enormes desde o final da distribuição. Digamos que você tenha um pool de 10 threads e observe o cronograma de reciclagem, construído com base nas métricas de tempo operacional e tempo de inatividade, que são coletadas a cada 15 segundos. Primeiro, você pode não perceber que um thread está paralisado ou que todos os 10 threads executaram simultaneamente grandes tarefas por um segundo e depois não fizeram nada por 14 segundos. Uma resolução de 15 segundos não permite ver um salto na utilização de até 100% e de volta a 0%, e o tempo de resposta sofre. , , 15 6 , .



, ( ) .

, RTMR SelfPing, ( 10 ), — . , 10 15 . , . , , 10 , , — . self-ping- CPU. , : , , . : , , . : . , 15- , — .

, , SelfPing , ? ? , LWTrace. , . -100 . . : ; — , , ; perf , , .

« », . , , . FIFO-. , , latency ( SPT SRPT). — . , , , . , « », .

, - product-form solution . M/ Cox /1/ PS . , (Coxian distribution) (Processor Sharing), , , . ? , . , , (. ) , , M/ M /1/ FIFO , , .

! , , , ! insensitivity property. , , , , . — M/M/∞. , . , product-form solution — BCMP .

. , (, ), , , ó . . Solução. $$$\mathbf{E}[T] = 1/3 \mathbf{E}[T_1] + 2/3 \mathbf{E}[T_2]$ . $$$\mathbf{E}[T_i] = 1/(\mu_i - \lambda_i)$ M/M/1/FCFS $$$\mathbf{E}[T] = 1/3 * 1/(3 - 3 * 1/3) + 2/3 * 1/(4 - 3*2/3) = 0.5$ .

, , . , .

1. , , , computer science, . Performance Modeling and Design of Computer Systems: Queueing Theory in Action (2013). - , . ó — .
2. A apresentação mais simples, na medida do possível, sem perda de significado, da apresentação dos clássicos da teoria que conheço no formato de vídeo-aula de Robert B. Cooper. Nessas palestras, ele conta de maneira inteligível quase todo o livro e tudo o que é necessário para entendê-lo.