A amostragem de tanques (por exemplo, "Amostragem de reservatório") é um algoritmo simples e eficiente para amostrar aleatoriamente um certo número de elementos de um vetor existente de tamanho grande e / ou desconhecido. Não encontrei nenhum artigo sobre esse algoritmo no Habré e, portanto, decidi escrevê-lo.
Então, do que estamos falando? Selecionar um elemento aleatório de um vetor é uma tarefa elementar:
A tarefa de "retornar K elementos aleatórios de um vetor de tamanho N" já é mais complicada. Aqui você já pode cometer um erro - por exemplo, pegue K primeiros elementos (isso viola o requisito de aleatoriedade) ou pegue cada um dos elementos com probabilidade K / N (isso viola o requisito de pegar exatamente K elementos). Além disso, é possível implementar uma solução formalmente correta, mas extremamente ineficaz "misture aleatoriamente todos os elementos e leve o K primeiro". E tudo se torna ainda mais interessante se adicionarmos a condição de que N é um número muito grande (não temos memória suficiente para salvar todos os N elementos) e / ou não é conhecido antecipadamente. Por exemplo, imagine que temos algum tipo de serviço externo que nos envia elementos um de cada vez. Não sabemos quantos deles aparecerão no total e não podemos salvá-los, mas queremos ter um conjunto de exatamente K elementos selecionados aleatoriamente dentre os recebidos a qualquer momento.
O algoritmo de amostragem de reservatório nos permite resolver esse problema nas etapas O (N) e na memória O (K). Nesse caso, não é necessário conhecer N antecipadamente, e a condição de amostragem aleatória de exatamente K elementos será claramente observada.
Vamos começar com uma tarefa simplificada.
Seja K = 1, ou seja, precisamos selecionar apenas um elemento de todos os recebidos - mas para que cada um dos elementos recebidos tenha a mesma probabilidade de ser selecionado. O algoritmo sugere a si mesmo:
Etapa 1 : aloque memória para exatamente um elemento. Guardamos nele o primeiro elemento que chegou.

Até agora, está tudo bem - apenas um elemento chegou até nós, com uma probabilidade de 100% (no momento), ele deve ser selecionado - está.
Etapa 2 : O segundo elemento recebido é reescrito com uma probabilidade de 1/2 como o selecionado.

Aqui também está tudo bem: até agora, apenas dois elementos chegaram até nós. O primeiro permaneceu selecionado com probabilidade de 1/2, o segundo reescreveu com probabilidade de 1/2.
Etapa 3 : o terceiro elemento recebido com probabilidade de 1/3 é reescrito como o selecionado.
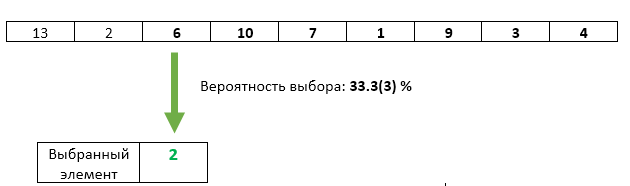
Está tudo bem com o terceiro elemento - sua chance de ser escolhida é exatamente 1/3. Mas de alguma forma violamos as chances iguais dos elementos anteriores? Não. A probabilidade de o item selecionado não ser sobrescrito nesta etapa é 1 - 1/3 = 2/3. E como na etapa 2 garantimos chances iguais para cada um dos elementos a serem selecionados, depois da etapa 3, cada um deles pode ser selecionado com uma chance de 2/3 * 1/2 = 1/3. Exatamente a mesma chance que o terceiro elemento.
Etapa N : com uma probabilidade de 1 / N, o número do elemento N é reescrito como o selecionado. Cada um dos itens anteriores que chegaram tem a mesma chance de 1 / N de permanecer selecionado.
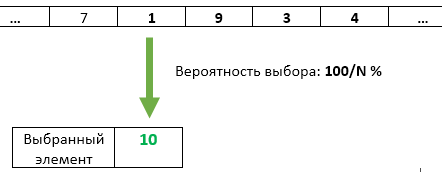
Mas foi uma tarefa simplificada, com K = 1.
Como o algoritmo mudará para K> 1?
Etapa 1 : Alocamos memória em K elementos. Escrevemos nele os primeiros K elementos que chegaram.

A única maneira de tirar K elementos de K chegou elementos é pegá-los todos :)
Etapa N : (para cada N> K): gere um número aleatório X de 1 a N. Se X> K, descartamos esse elemento e prosseguimos para o próximo. Se X <= K, reescreva o elemento com o número X. Como o valor de X será uniformemente aleatório no intervalo de 1 a N, na condição X <= K, ele será uniformemente aleatório no intervalo de 1 a K. Assim, garantimos a uniformidade seleção de itens regraváveis.

Como você pode ver, todo próximo elemento que vem tem menos e menos chance de ser selecionado. No entanto, sempre será exatamente K / N (como para cada um dos elementos anteriores chegados).
A vantagem desse algoritmo é que podemos parar a qualquer momento, mostrar ao usuário o vetor atual K - e este será o vetor de elementos aleatórios selecionados honestamente da sequência de elementos que chegou. Talvez isso seja adequado ao usuário, ou talvez ele queira continuar processando os valores recebidos - podemos fazer isso a qualquer momento. Nesse caso, como mencionado no início, nunca usamos mais do que memória O (K).
Ah, sim, eu esqueci completamente, a função
std :: sample , que faz exatamente o que é descrito acima, foi finalmente incluída na biblioteca C ++ 17 padrão. O padrão não obriga a usar apenas a amostragem de reservatório, mas obriga a trabalhar nas etapas O (N) - bem, é improvável que os desenvolvedores de sua implementação na biblioteca padrão escolham algum algoritmo que use mais do que memória O (K) (e menos também falhará - o resultado precisa ser armazenado em algum lugar).
Materiais relacionados